Ionosphere Scintillation-Induced
Phase Transitions (Cycle Slips)
in Triple-Frequency GPS Measurements

Brian Breitsch, Jade Morton, Dongyang Xu
24 January 2020

ION ITM/PTTI 2020
are ionosphere-induced phase transitions?
What
Why
How
Outline
are they so difficult to deal with?
can we mitigate their impact?
are ionosphere-induced phase transitions?
What
Why
How
Outline
are they so difficult to deal with?
can we mitigate their impact?
Ascension Island - 2013-10-05 - G24


(typically equatorial) ionosphere plasma bubbles / structures
signal diffraction
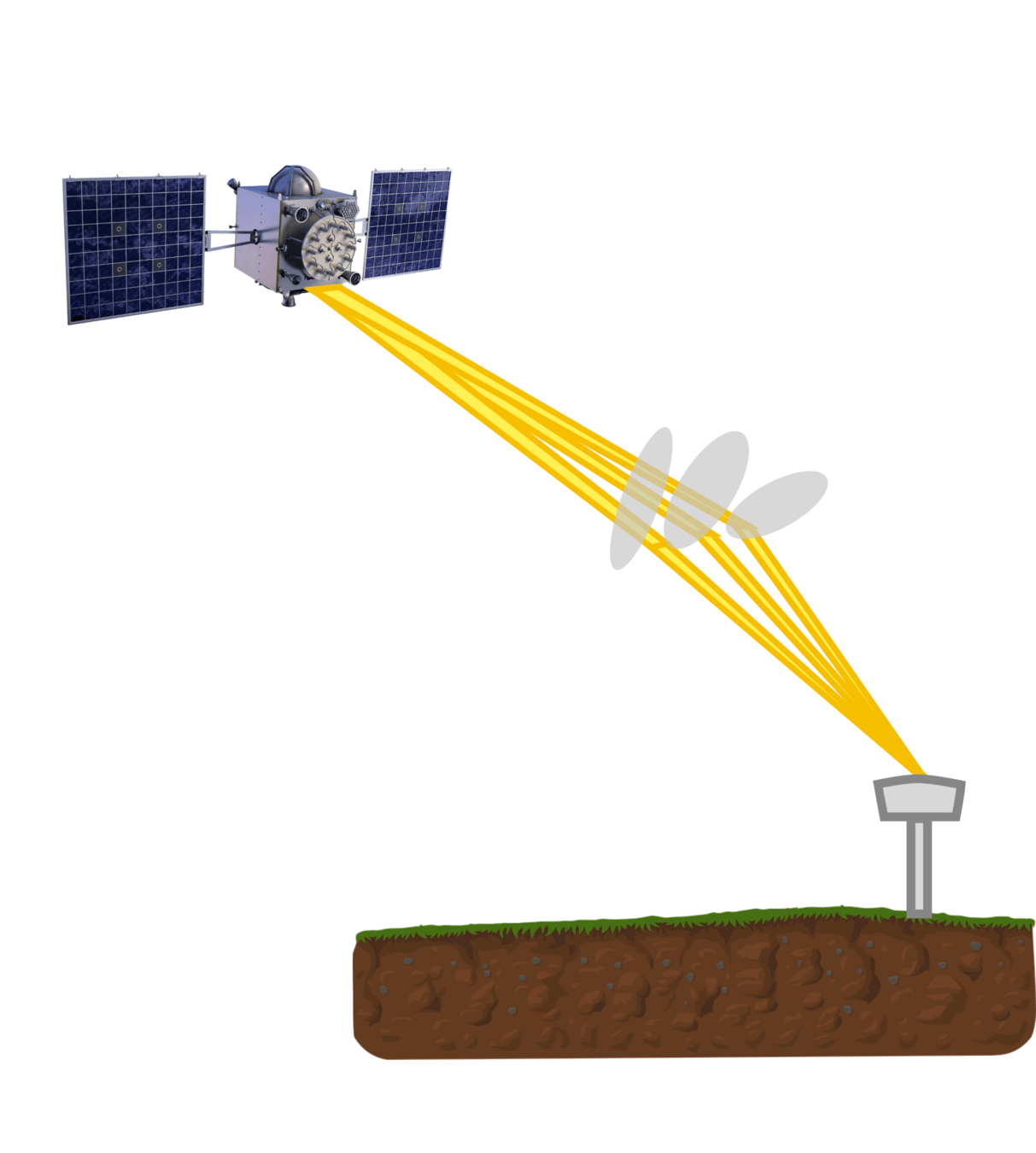
Ionosphere Scintillation
[Xu et al 2017]
Signal Model

IONOSPHERE EFFECTS
BIASES
NONDISPERSIVE EFFECTS
phase model
ionosphere effect
REFRACTIVE
DIFFRACTIVE
WARNING: \(I_\text{diffr}\) may contain phase transitions...
...but why?
Ionosphere Diffraction Simulations


instantiate realistic phase screen structure \(\bar{\phi}\) from stochastic model


propagate using parabolic wave equation methods
generate complex field \(\Psi(t)\) at the receiving antenna
Simulated Phase Transitions
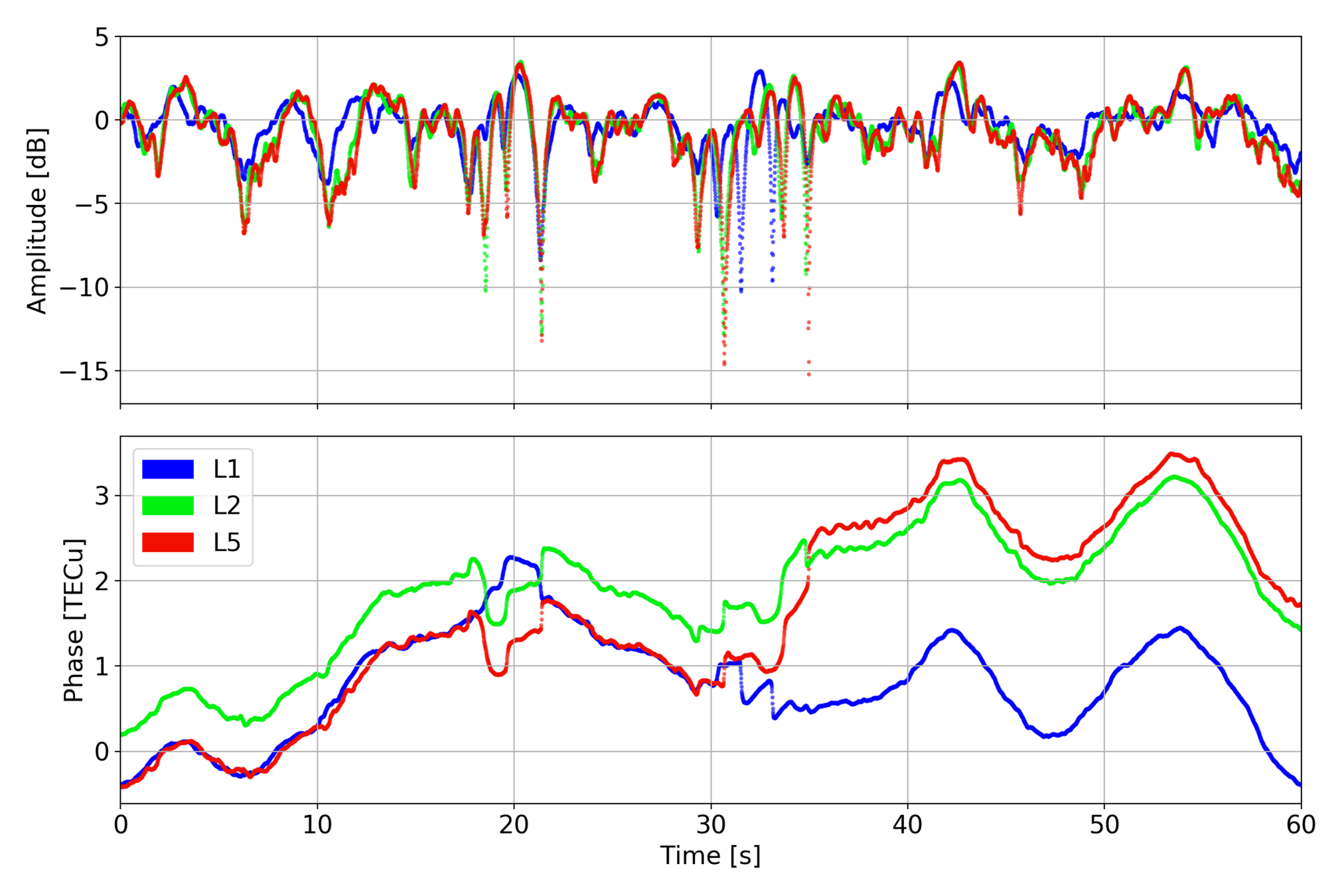
Most of common variation in \(\phi_k(t)\) is due to ionosphere refraction, which is approximately captured by the model phase screens \(\bar{\phi}(t)\).


[Rino et al 2017]
Origin of Phase Transitions
Assume the phase screen structure approximates refractive phase, i.e. \(I_\text{refr} \propto \bar{\phi}\).
Then \(\tilde{\phi}(t) = \text{unwrap}\left(\angle \tilde{\Psi}(t) \right)\) is the diffractive phase and \(I_\text{diffr} \propto \tilde{\phi}\)
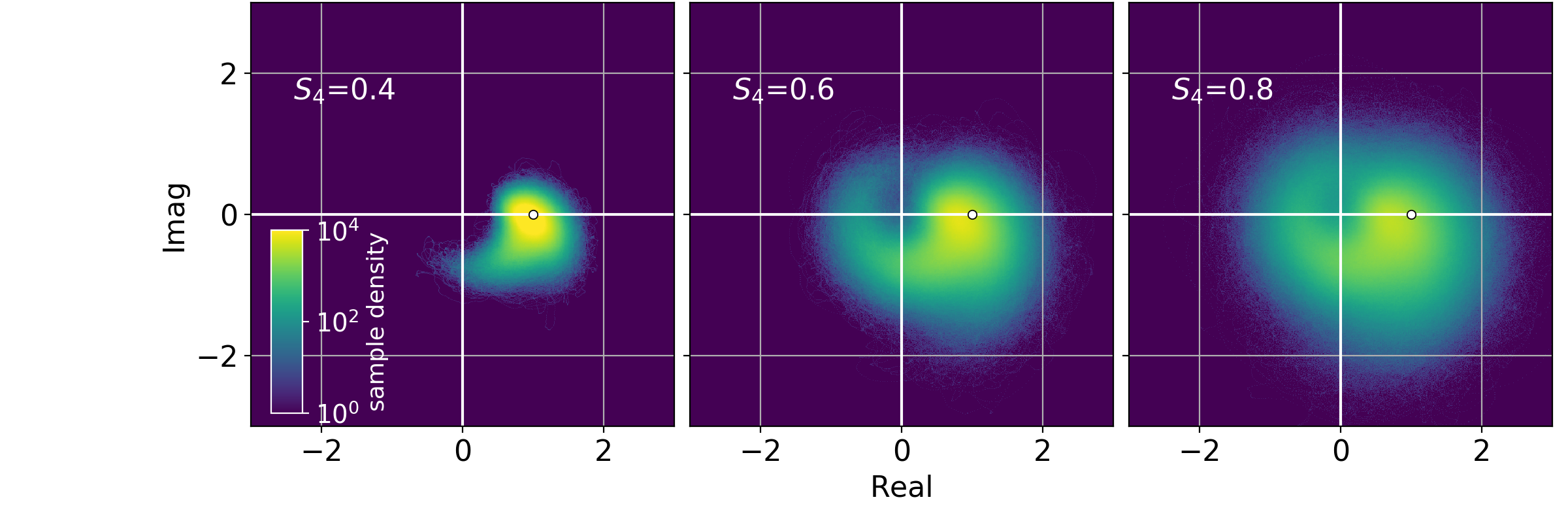
histograms of \(\tilde{\Psi}\)
We can decompose \(\Psi(t)\) as \(\Psi(t) = \tilde{\Psi}(t) \exp(i\bar{\phi}(t))\).


Phase Transitions
not instantaneous!
phase rate-of-change as cycle slip indicator would produce many false positives!

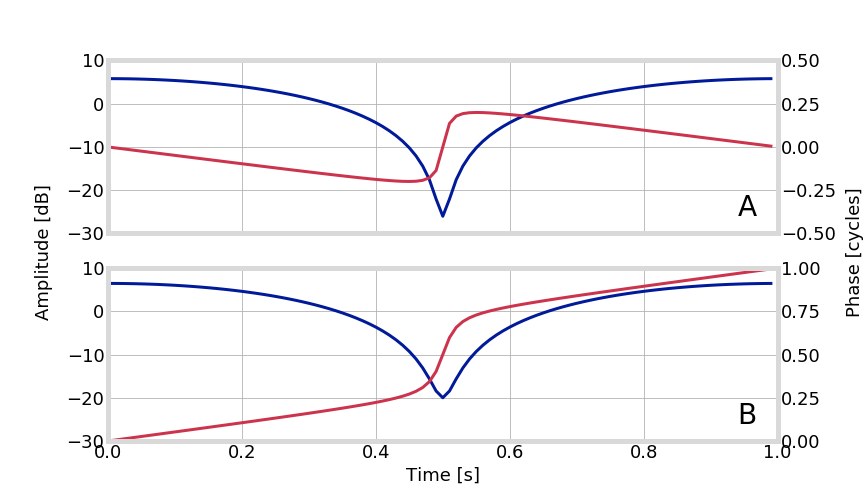
singularity at origin causes phase bifurcation
Phase Transitions as Cycle Slips
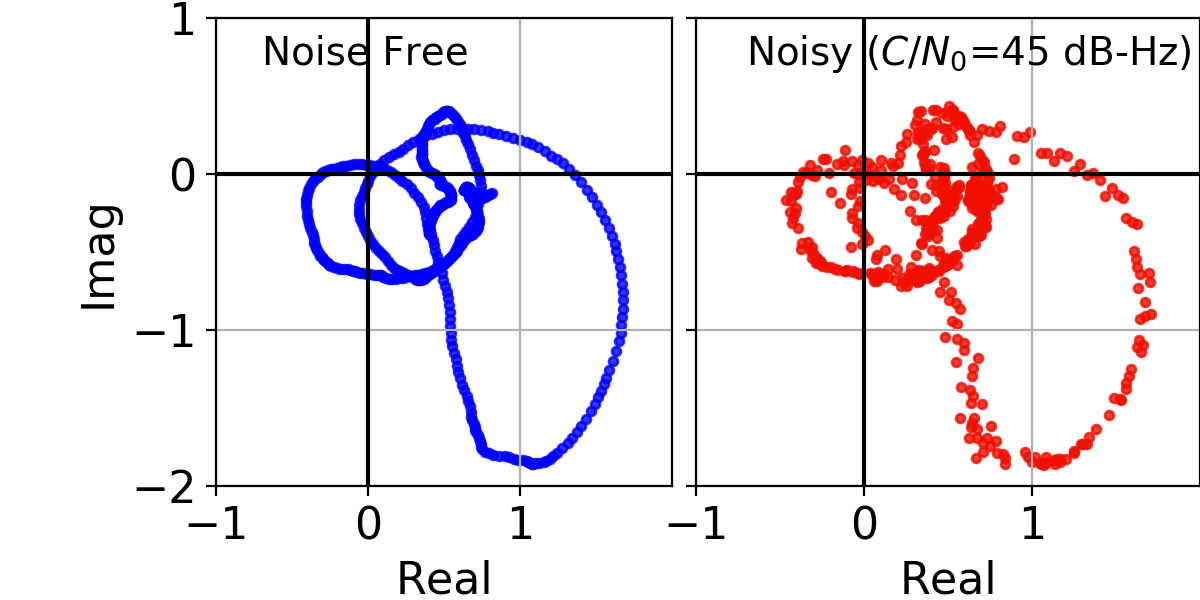
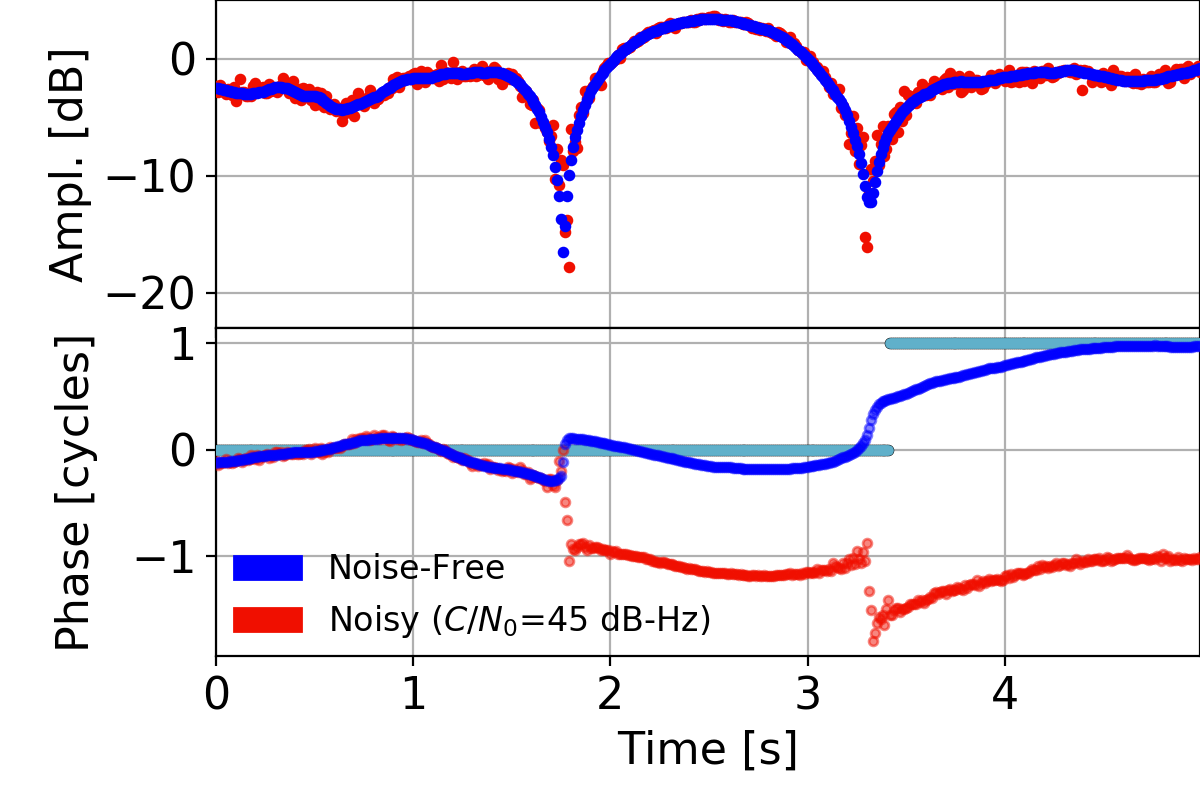
[phase transitions] occur gradually over many samples...[they are] distinct from cycle slips, which are abrupt phase changes of a cycle (or more)
- Carrano et al 2013
Phase transitions and cycle slips due to other factors are often indistinguishable
- Me (Brian) 2020


"[The] increased measurement noise associated with an active ionosphere makes correcting cycle slips an ongoing challenge which requires further investigation."
- Banville 2010



"...precise navigation is possible under strong scintillation conditions as long as the problem with the cycle slips could be properly addressed."
- Juan et al 2018


are ionosphere-induced phase transitions?
What
Why
How
Outline
are they so difficult to deal with?
can we mitigate their impact?
Cycle Slip Detection
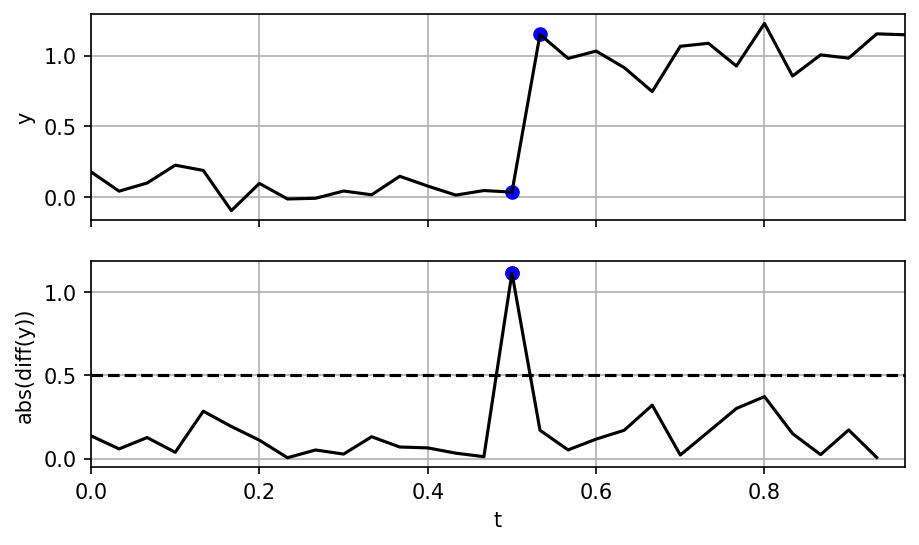
Cycle Slip Detection
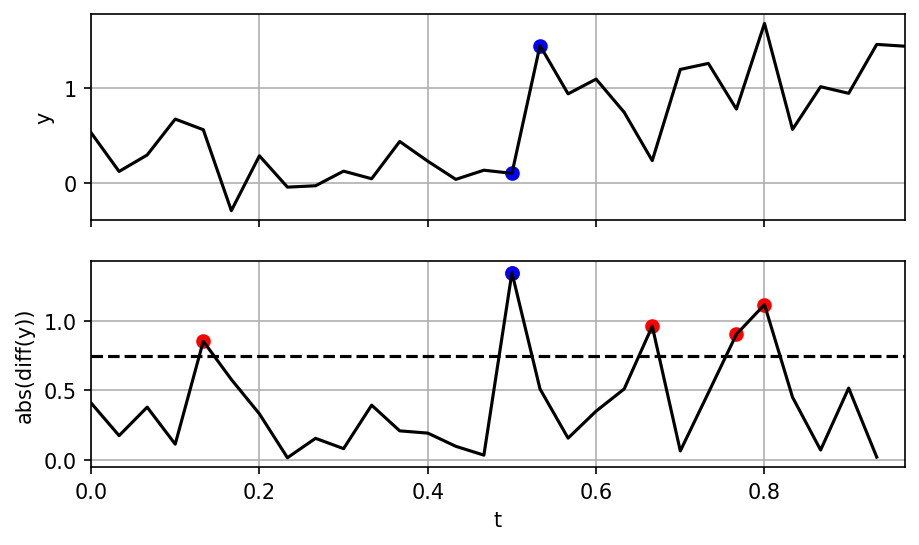
Cycle Slip Detection
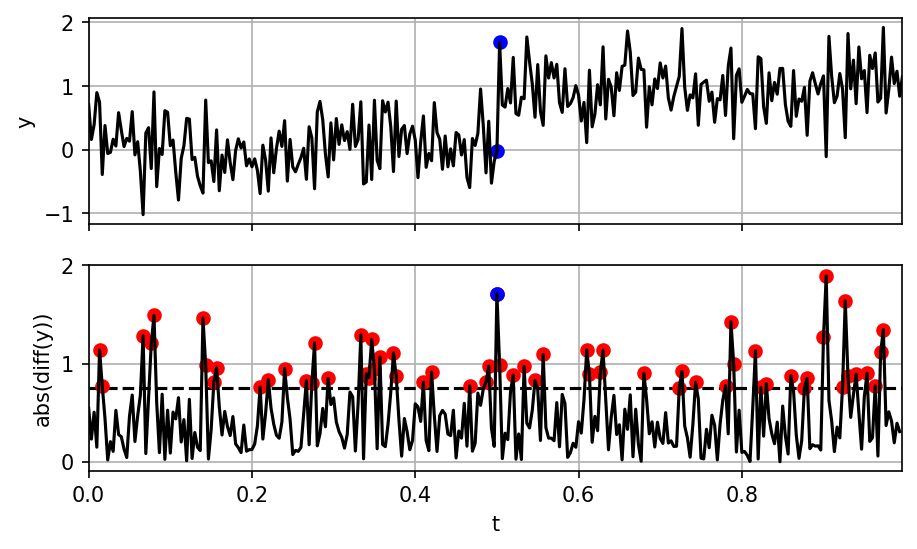
Cycle Slip Detection
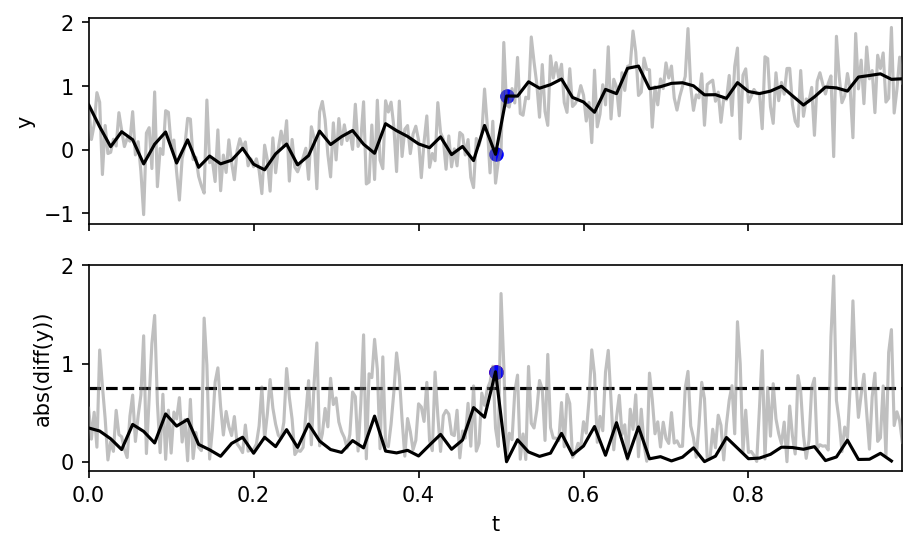
Cycle Slip Detection
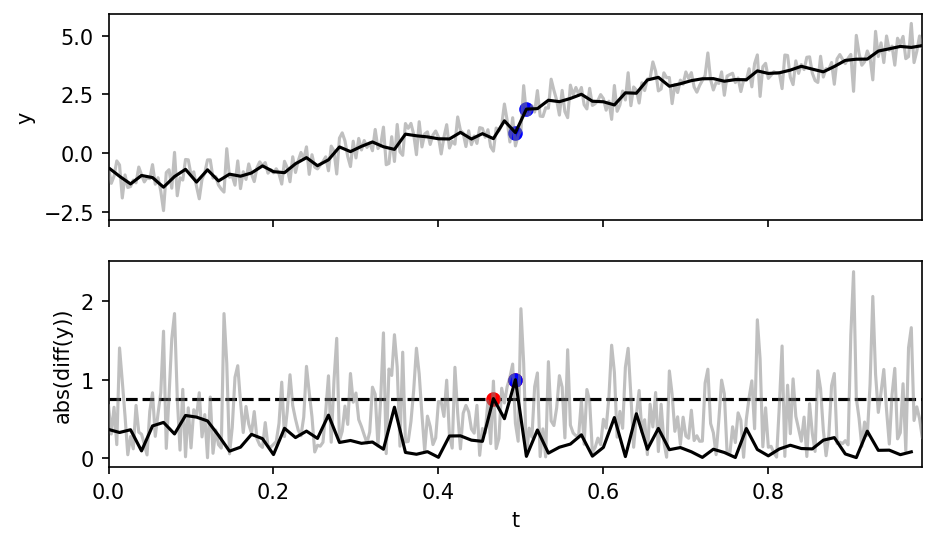
Cycle Slip Detection
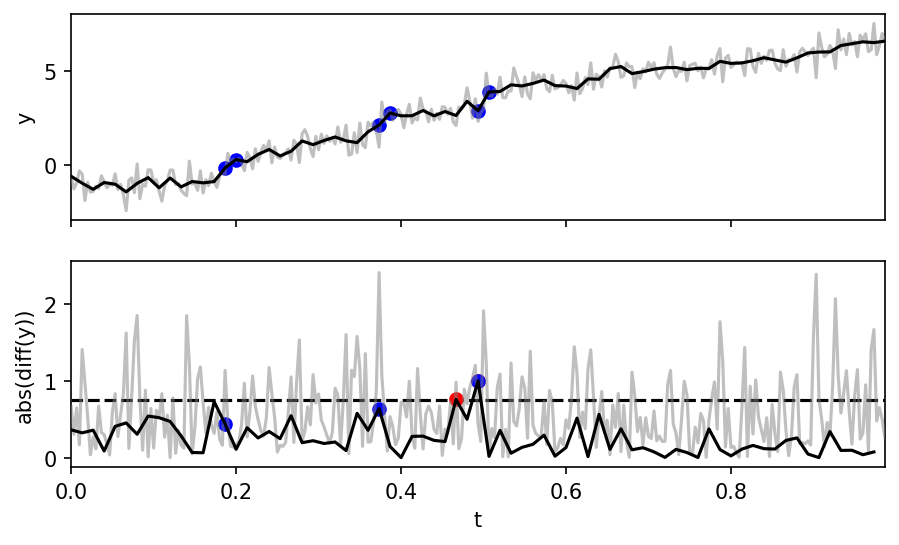
Things that make cycle slip detection hard
Effects of ionosphere diffraction
large phase noise
unknown trends / dynamics
frequent / consecutive slips
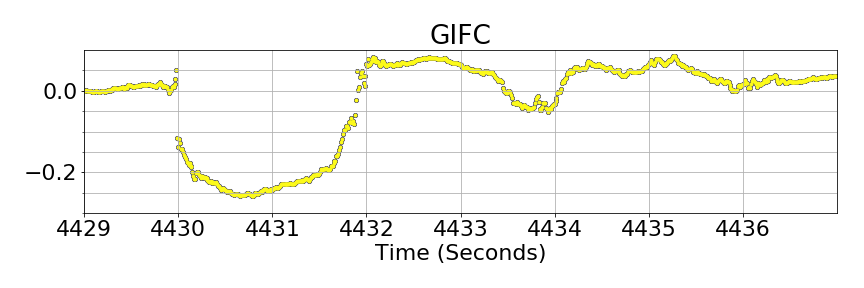
Geometry-Free Cycle Slip Detection
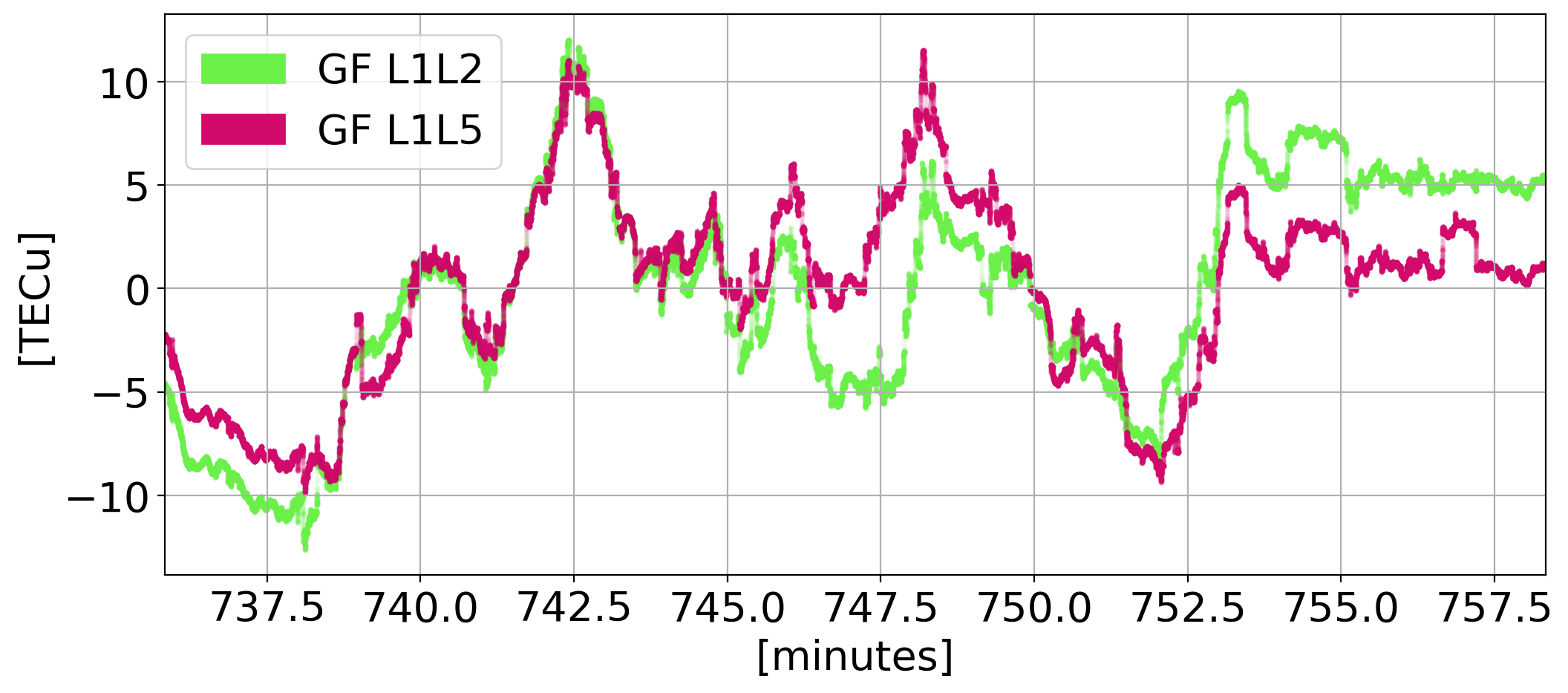
Geometry-Free combination not viable during diffraction
are ionosphere-induced phase transitions?
What
Why
How
Outline
are they so difficult to deal with?
can we mitigate their impact?
Mitigation Strategies
- multi-frequency observations
- triple-frequency [de Lacy 2012, etc.]
- quadruple-frequency [Juan et al 2019]
- geodetic detrending [Juan et al 2017]
- cascaded detection [Qile Zhao 2014]
- first remove easy-to-detect slips
- allows detection of weaker signatures
- expanding window of observations [Tao Li 2018]
What remains is to carfully apply these techniques to the diffraction-induced cycle slip problem.
Linear Combinations of Phase
Ionosphere-Free
Geometry-Free
Geometry-Ionosphere-Free
not so useful during diffraction
need to know your clocks!
need triple-frequency
Linear Combinations of Phase
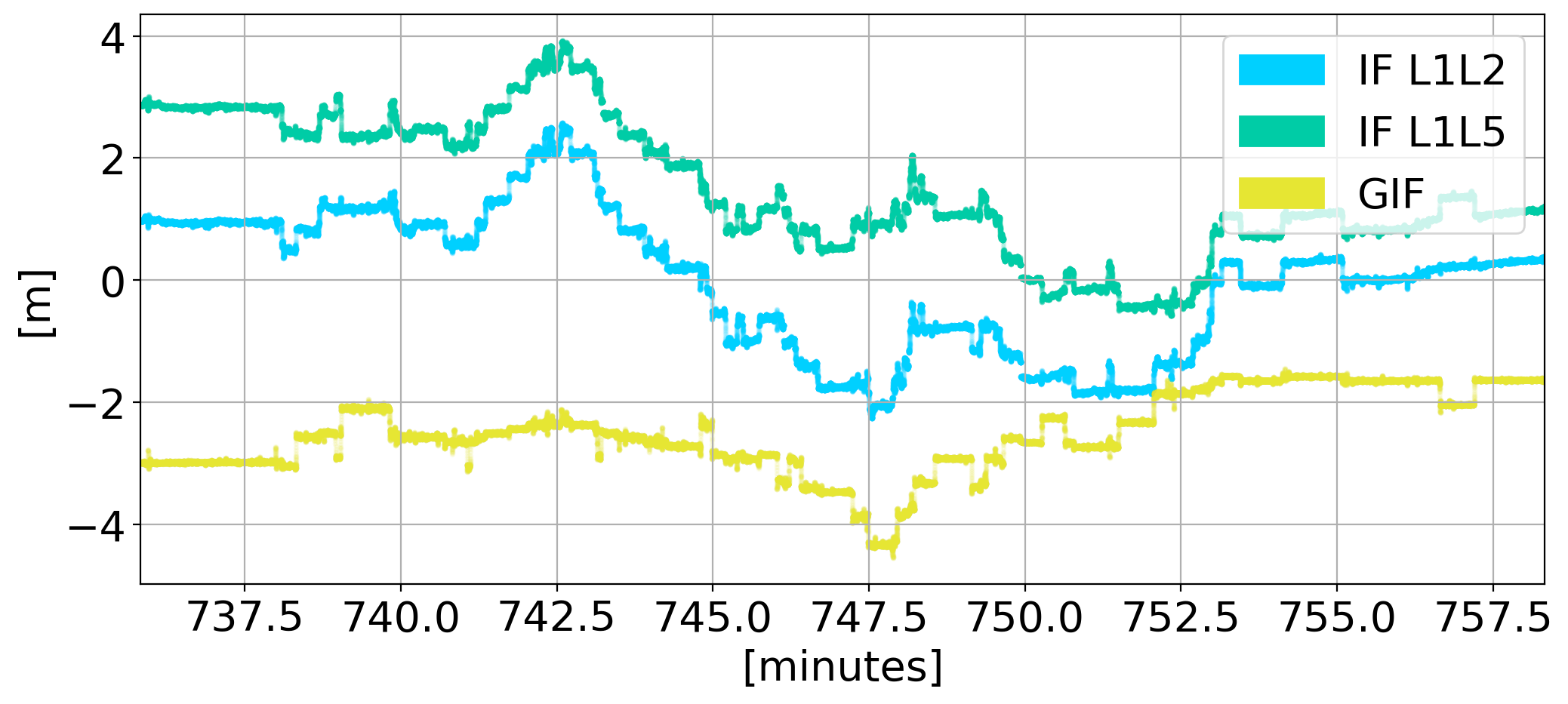
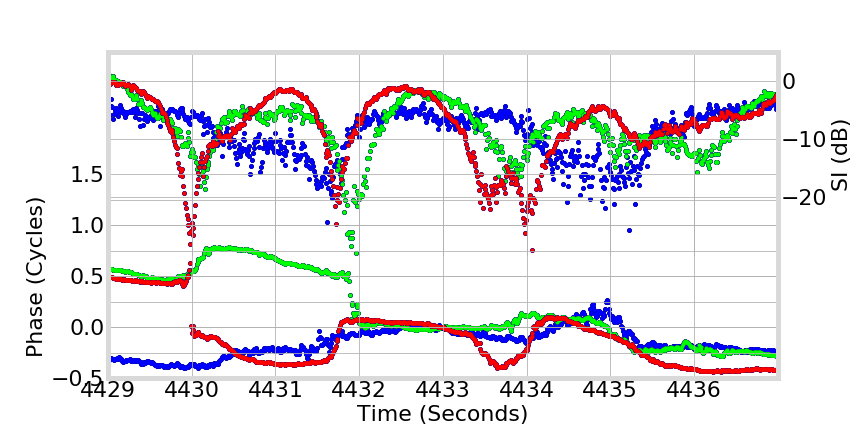
Septentrio PolaRxS - Hong Kong - 2013-10-05 - G24
Slip Detectability

(1, 1, 1)
(0, 1, 1)
(1, 0, 0)
(1, 1, -)
(1, -, 1)

cycle-slip combinations
Geometry-Ionosphere-Free Combination
L5
L2
L1

Key Points

GNSS phase measurements are plagued by diffraction-induced cycle slips (and phase transitions) during strong ionosphere scintillation
Diffraction-induced cycle slip detection is challenging
- methods that only use GF combination are not viable
- many consecutive slips with large noise residuals
A combination of strategies will be necessary to detect cycle slips during diffraction
- triple-frequency offers unique advantages
- cycle slip combinations (1, 1, 1), (0, 1, 1), and (1, 0, 0) are especially challenging

References

Xu, Dongyang, and Yu Morton. "A semi-open loop GNSS carrier tracking algorithm for monitoring strong equatorial scintillation." IEEE Transactions on Aerospace and Electronic Systems 54.2 (2017): 722-738.
Rino, Charles, et al. "A New GNSS Scintillation Model." Proc. ION GNSS. 2017.
de Lacy, Maria Clara, Mirko Reguzzoni, and Fernando Sansò. "Real-time cycle slip detection in triple-frequency GNSS." GPS solutions 16.3 (2012): 353-362.
Wang, Yaoding, et al. "Real-Time Quadruple-Frequency Cycle Slip Detection and Repair Algorithm Based on the Four Chosen Linear Combinations." IEEE Access 7 (2019): 154697-154710.
Juan, José Miguel, et al. "Feasibility of precise navigation in high and low latitude regions under scintillation conditions." Journal of Space Weather and Space Climate 8 (2018): A05.
Zhao, Qile, et al. "Real-time detection and repair of cycle slips in triple-frequency GNSS measurements." GPS Solutions 19.3 (2015): 381-391.
Li, Tao, and Stavros Melachroinos. "An enhanced cycle slip repair algorithm for real-time multi-GNSS, multi-frequency data processing." GPS Solutions 23.1 (2019): 1.
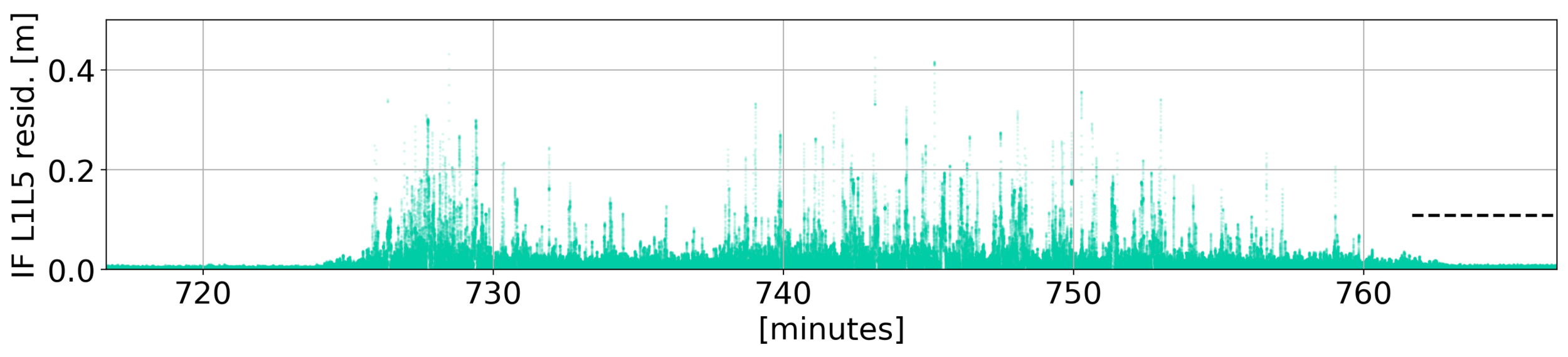
Cycle Slip Detection
Attempted removal in real scintillation data (Hong Kong, Septentrio ground antenna)
phase transitions
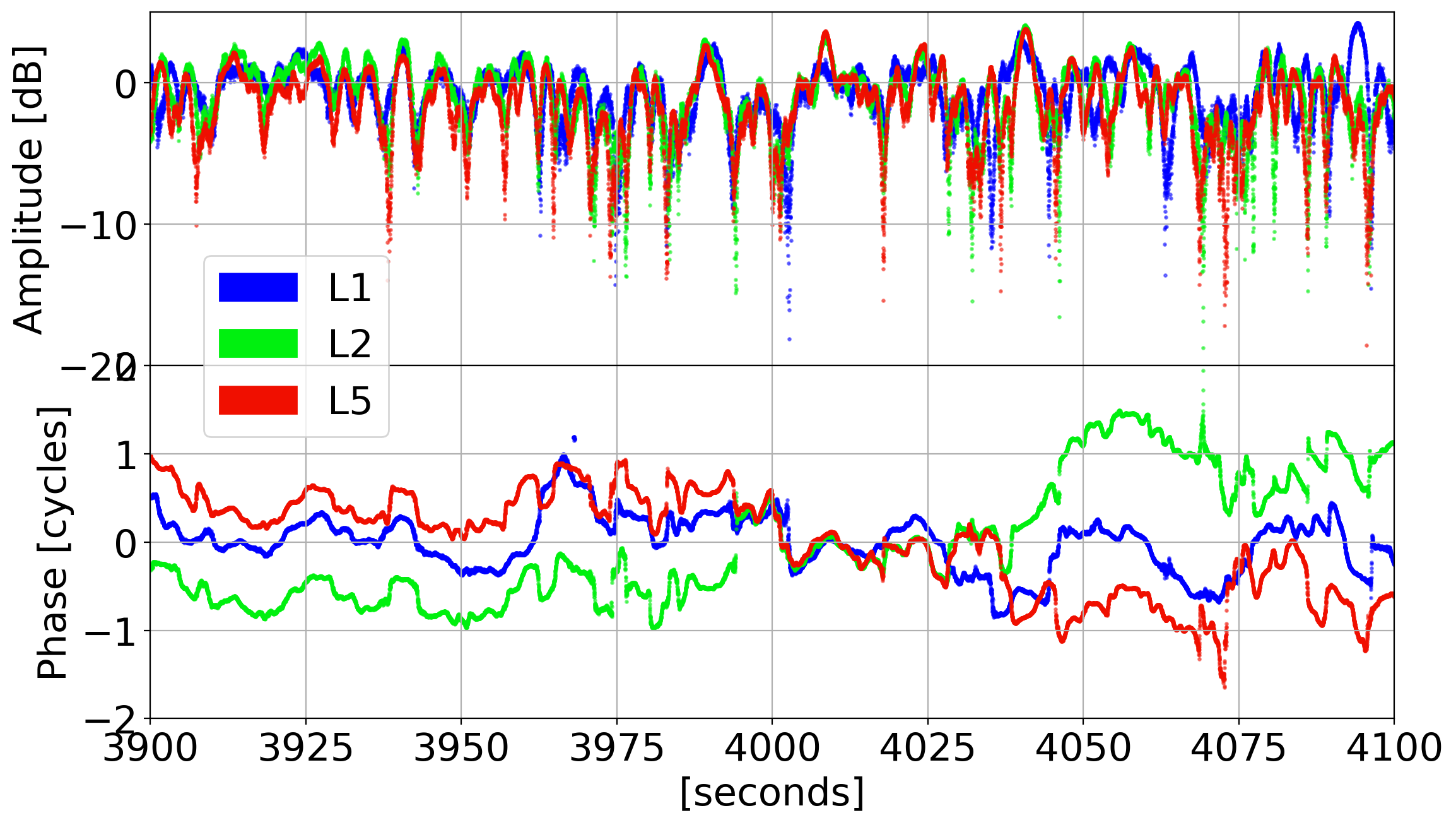
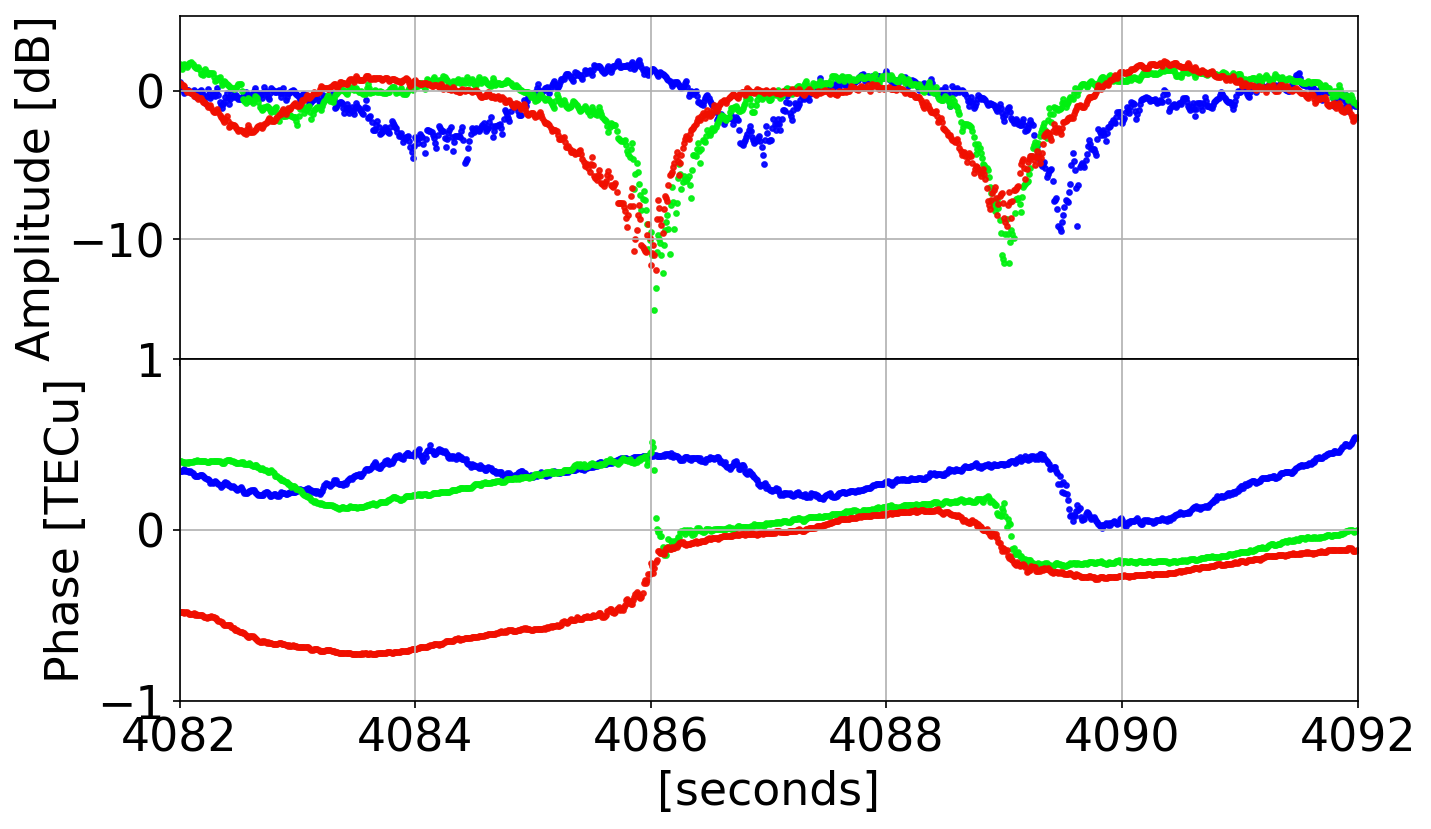
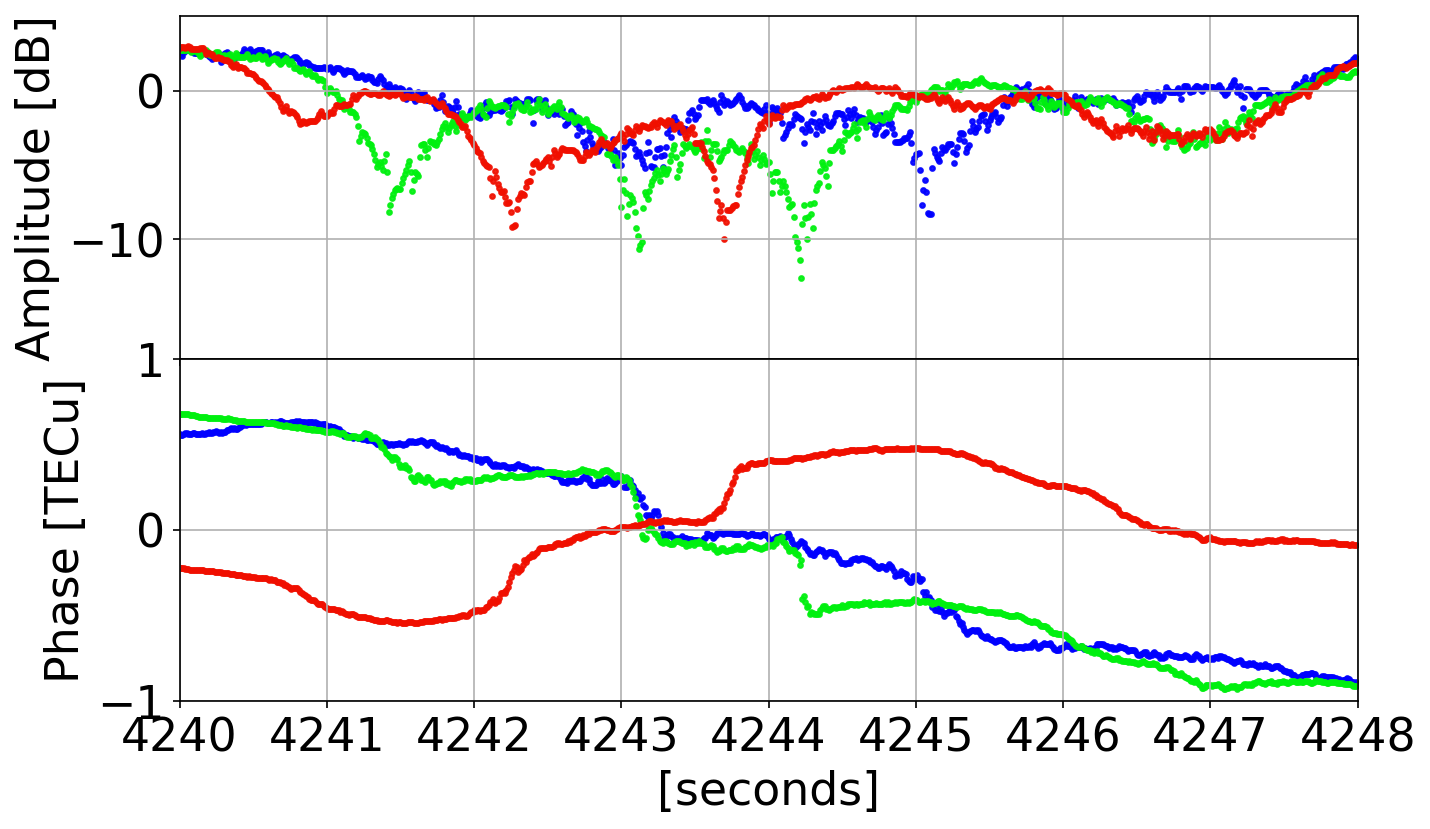
Phase Behavior in Real Data
L5
L2
L1

Phase Behavior in Real Data
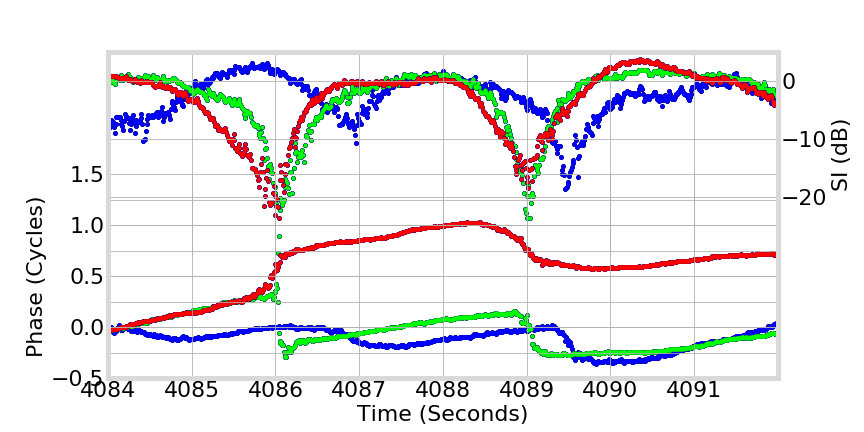
L5
L2
L1
Phase Behavior in Real Data
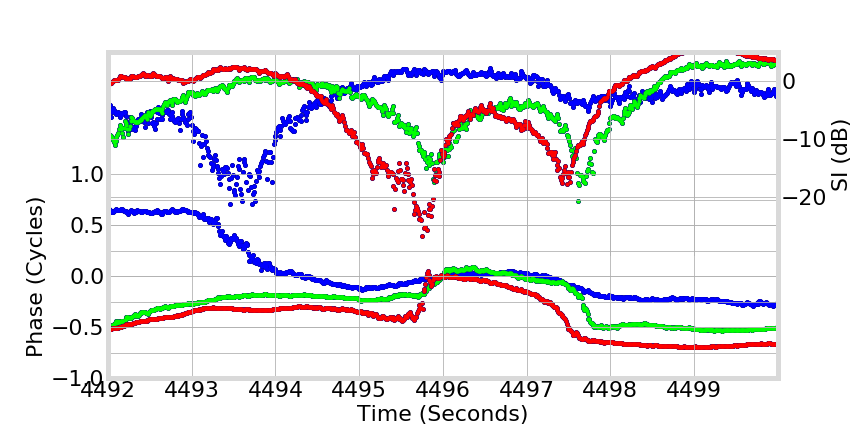
L5
L2
L1
Phase Transitions
Linear Combinations
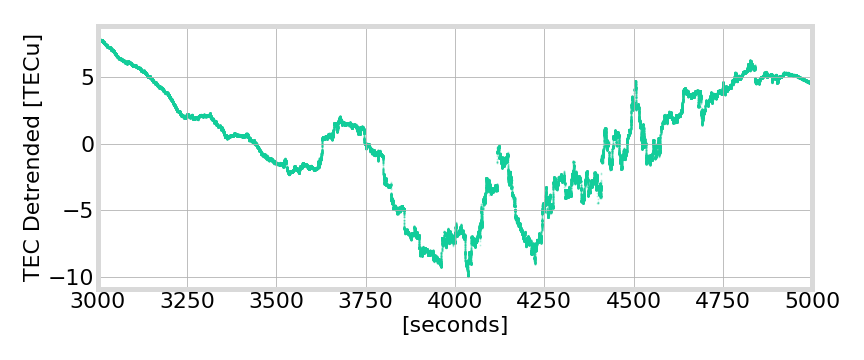
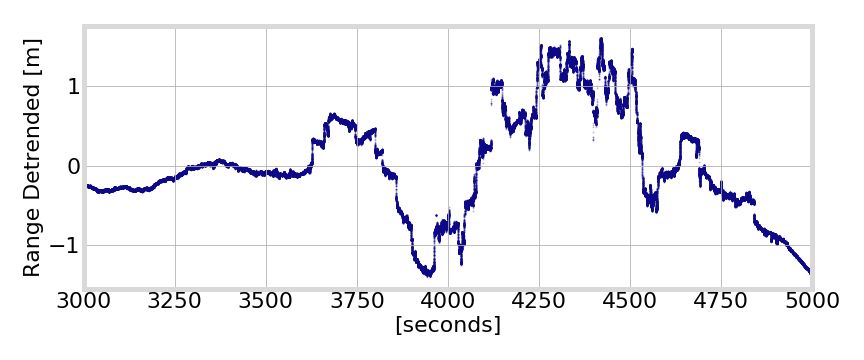
Ionosphere Scintillation
L5
L2
L1
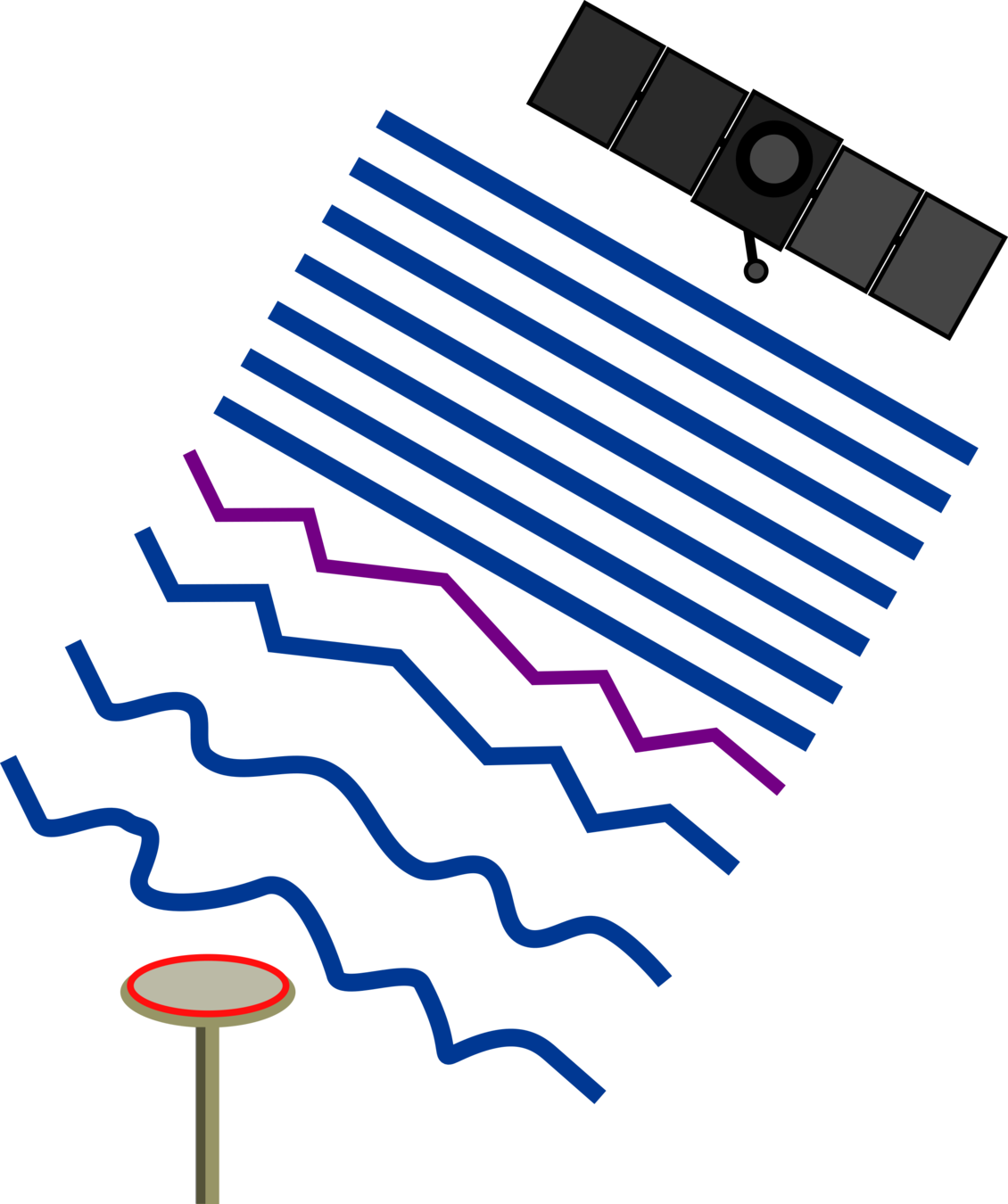
ionosphere phase screen
2013, Ascension Island, PRN 24
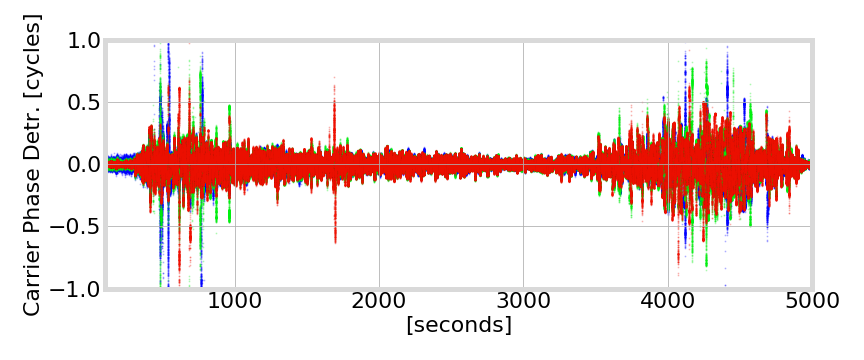
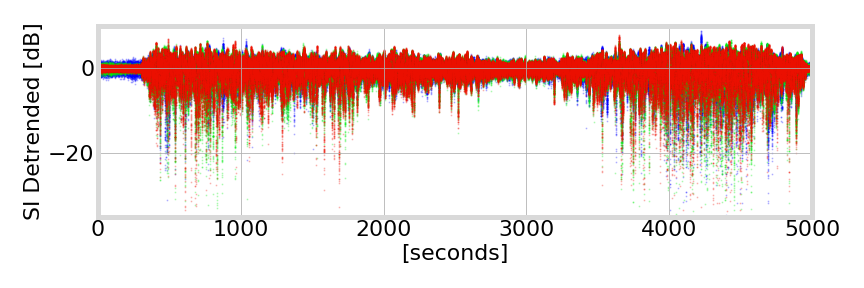

fading of 15 to 20 dB or more in signal amplitude
Deep Fading
canonical fades: associated with half-cycle phase changes
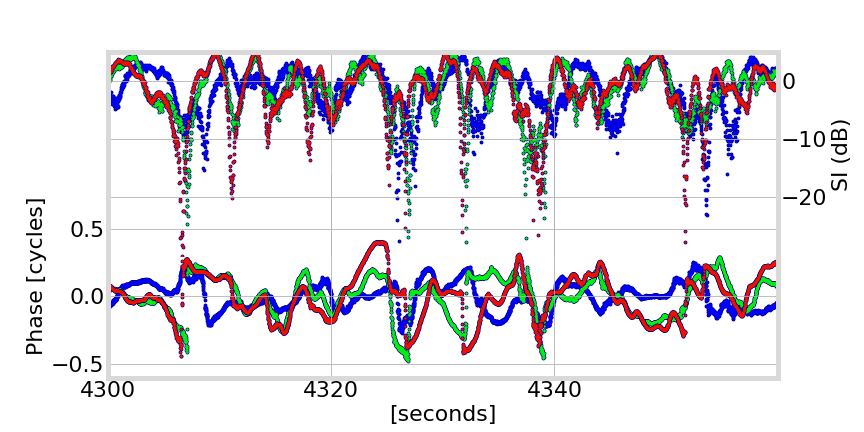
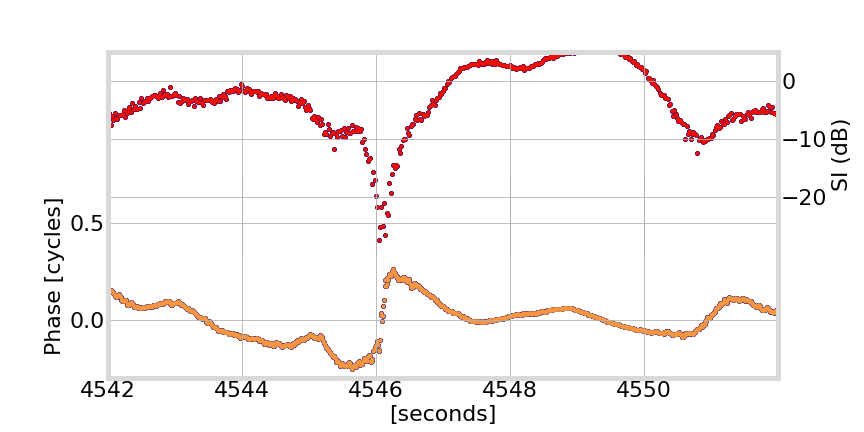
L5
L2
L1
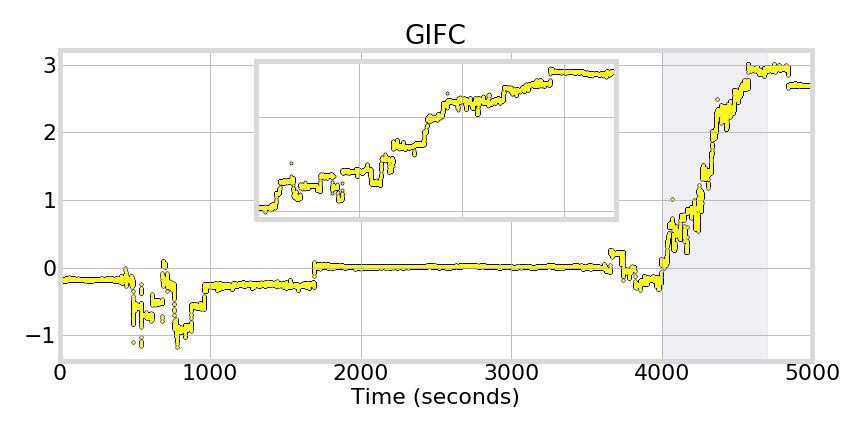
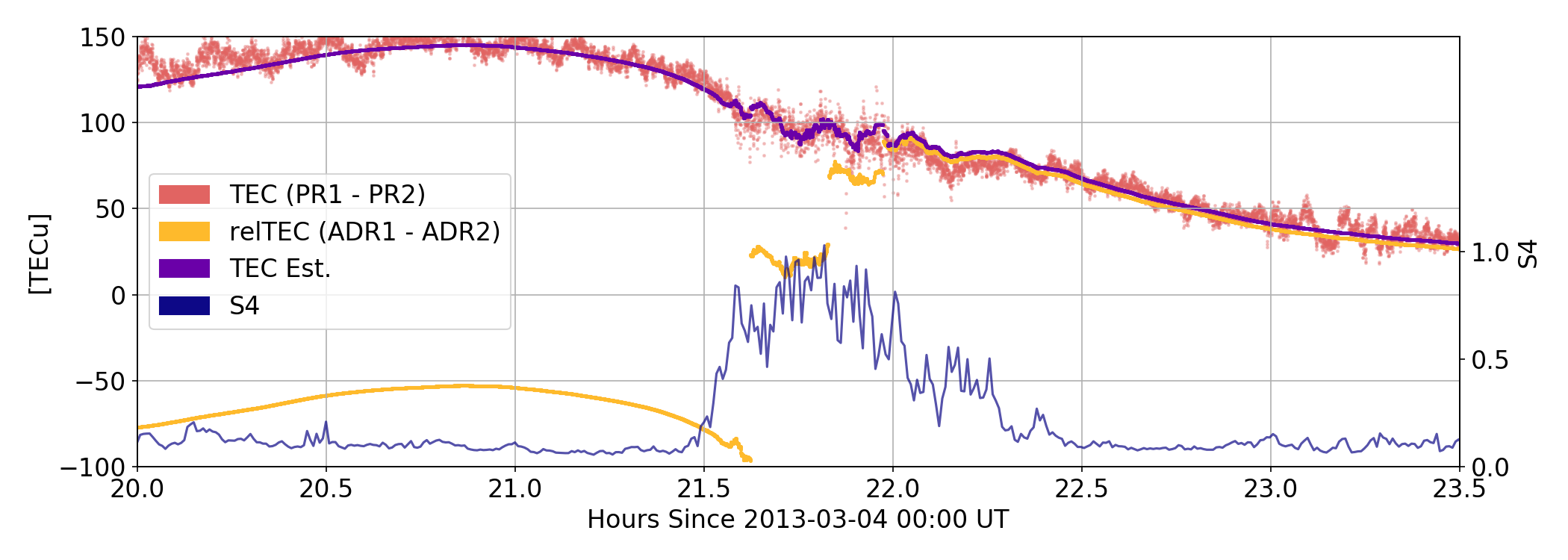
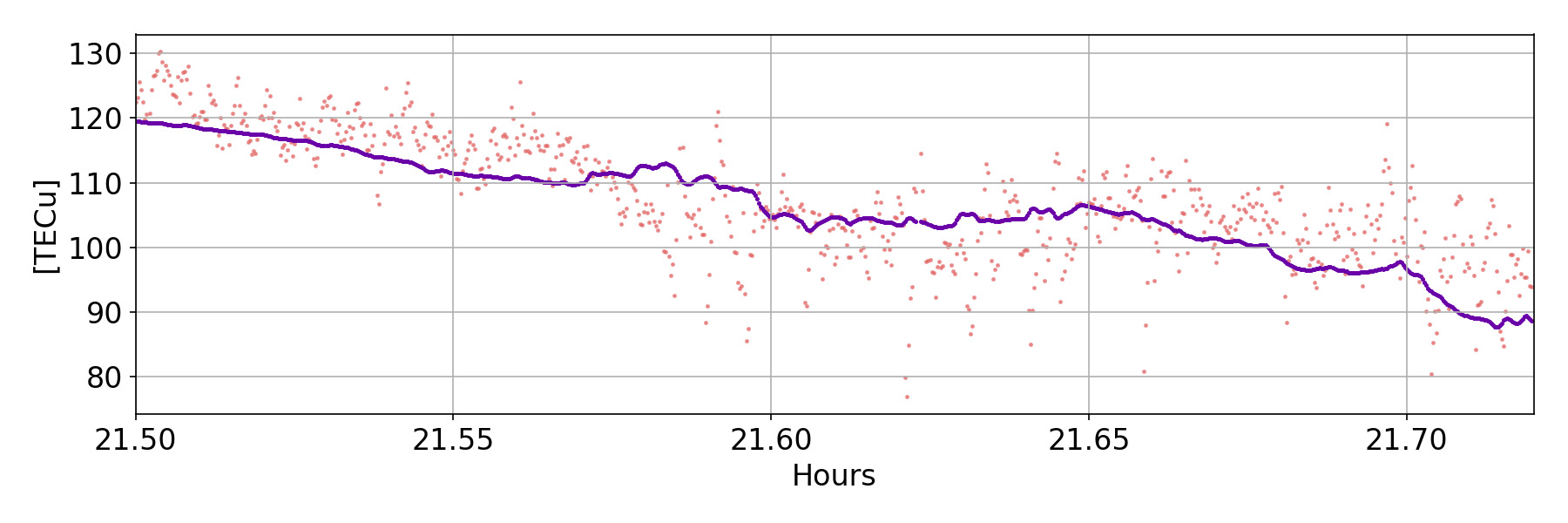
Simulating Scintillation
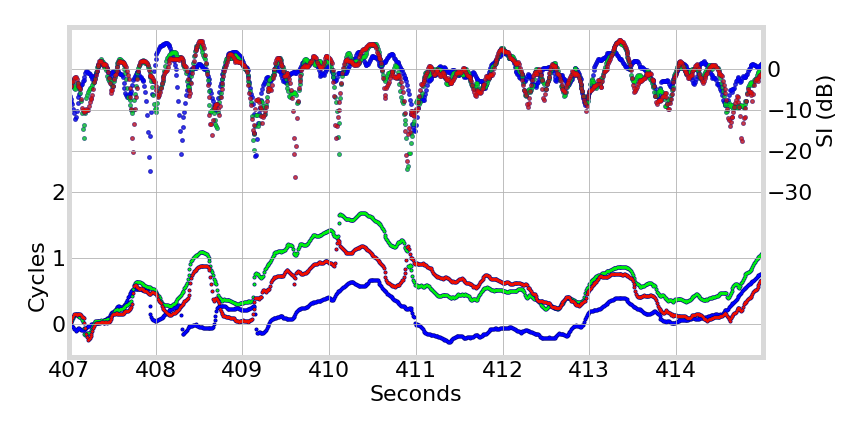
shows validation of occurrence of full-cycle transitions during canonical fades
simulation

Ionosphere Scintillation-Induced Phase Transitions in Triple-Frequency GNSS
By Brian Breitsch
Ionosphere Scintillation-Induced Phase Transitions in Triple-Frequency GNSS
ION ITM meeting 2020
- 609



