AP325
10^11
目錄
演算法(algorithm)
時間複雜度（time complexity）
空間複雜度（space complexity）
APCS亂炸
演算法
至今為止，我們學了很多東西
stack,queue,struct,DP......
這些都是演算法
但演算法的實際意義到底是什麼？
演算法
今天起飛跟嘎米想吃滷肉飯
input(輸入)
output(輸出)
+
演算法
演算法
有很多種拿到滷肉飯的方式
演算法
自己做
去實體店家買
Uxer eat
搶劫
很明顯，每種方法的速度都不同
要付出的代價也不同
演算法
這就是為什麼
會出現時間複雜度跟空間複雜度這兩個東西
時間複雜度
先來看看維基百科的定義：
蛤？就這樣？
時間複雜度
<time.h>
如何計算程式的執行時間
#include <time.h>
#include <iostream>
using namespace std;
int main() {
clock_t start, finish; //clock_t表示1秒有多少計時單元
start = clock(); //毫秒
int ex;
cin>>ex;
for(int i=0;i<ex;i++){
ex++;
}
finish=clock();
cout<<finish-start<<endl;
}時間複雜度
有一個嚴肅的問題：變因過多
會因為電腦效能、系統環境、程式的執行條件、其他背景過程的干擾而受到影響
需要實際測量才能知道
有沒有其它方法？
時間複雜度
在學習其他方法之前，我們要先了解T(n)是什麼
假設基礎運算都是1單位時間
宣告 = 賦值 = 運算 ... 皆為一單位時間
int a;
a = 1;
a += 5;時間複雜度
f(n)：基礎運算次數，取決於演算法的邏輯和輸入量大小nnn
tb：每次基礎運算所需的固定時間（假設硬體條件不變）
將T(n)表示為基礎運算的函數
對於輸入量n，程式的總執行時間可以表示為：
T(n) = f(n) \cdot t_b
時間複雜度
多少單位？
void f1(int n){
cout<<n<<endl;
}void f2(int n){
int i,sum;
sum=0;
for(i=0;i<n;i++){
sum+=i;
}
cout<<sum<<endl;
}T(n)=3n+6
T(n)=1
時間複雜度
實際計算時我們不需要這麼詳細的數值
只需要粗略估計而已
所以發展出新的符號
O(n)
蛤？
時間複雜度
讓T(n)以更簡單的方式呈現：
- 將 T(n) 分類
- 捨去不重要的項
- n 足夠大時，兩個函式有差不多的趨勢
時間複雜度
分類方式：
同類
f(n)=2, g(n)=1
f(n)=3n+6, g(n)=n
同類
f(n)=n, g(n)=n^2
不同類
時間複雜度
複雜度以 O(f(n))來表示，
其中習慣上以 n 來表示資料量，而 f(n)是 n 的函數，
複雜度的意義是
當資料量 為 n 時，這個程式(演算法)的執行時間(執行指令數)
不超過 f(n)的某個常數倍
蛤？
時間複雜度
借用剛剛的例子：
| 數量/方式 | 自己做 | 實體店家 | Uxer eat | 搶劫 |
|---|---|---|---|---|
| 1碗 | 60min | 30min | 20min | 1440min |
| 10碗 | 60*10min | 30min | 20min | 1440min |
| n碗 | 60*n min | 30min | 20min | 1440min |
時間複雜度
借用剛剛的例子：
如果我們選擇實體購買/Uxer eat/搶劫，
所要取得的時間不受想要的數量影響
畢竟一次可以買很多碗滷肉飯對叭？
此時所花的時間複雜度就是O(1)
時間複雜度
很明顯的
輸入 n 個數量需求，拿到飯的時間就會隨著 n 成倍數成長
如果我們選擇自己做？
那就是O(n)
時間複雜度
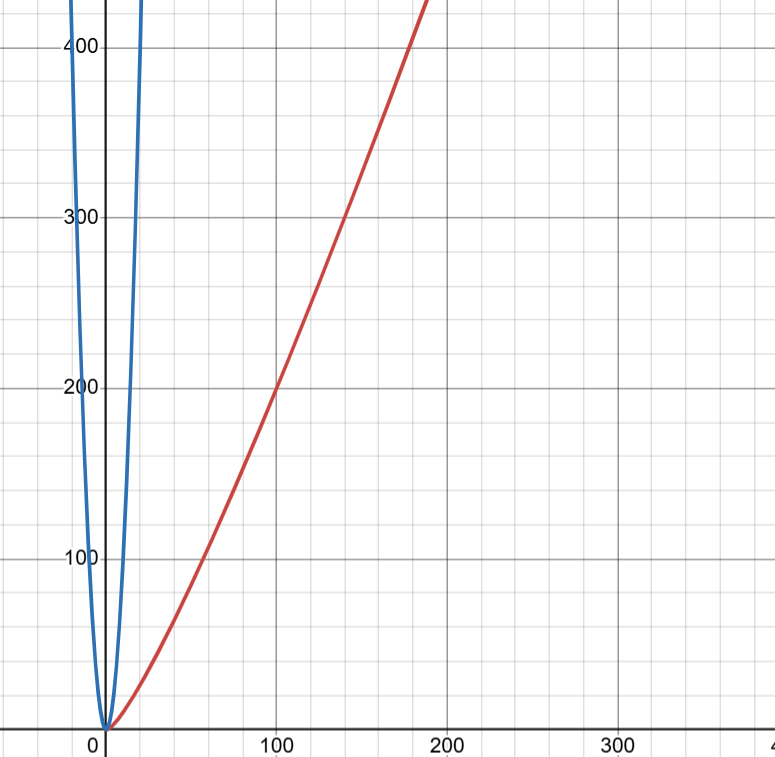
大 O 符號是用來描述一個演算法在輸入 n 個東西時，總執行時間與 n 的關係
時間複雜度
- 忽略低次項與常數項
- 聚焦於最壞情況
最重要的兩點：
時間複雜度
f(n)=2n+1
O(n)
f(n)=\log_{2} n
O(\log_{}n)
時間複雜度
複雜度以 O(f(n))來表示，
兩個函數相加的O等於比較大的函數。
若當 n 足夠大的時候 f(n)>=g(n)，
則 O(f(n)+g(n)) = O(f(n))。
時間複雜度
f(n)=n
g(n)=n^2
<
f(n)=n!
>
O(n!)
O(n^2)
g(n)=n^2
f(n)=n\log_{}n
>
g(n)=n^2
時間複雜度
O(n\log_{}n)
時間複雜度
f(n)=2^n
g(n)=n^2
>
時間複雜度
O(2^n)
時間複雜度
多少O？
void f3(int n){
int i,j;
for(i=0;i<n;i++){
for(int j=0;j<n;j++){
cout<<"*";
}
cout<<"\n";
}
}O(n)=n^2
時間複雜度
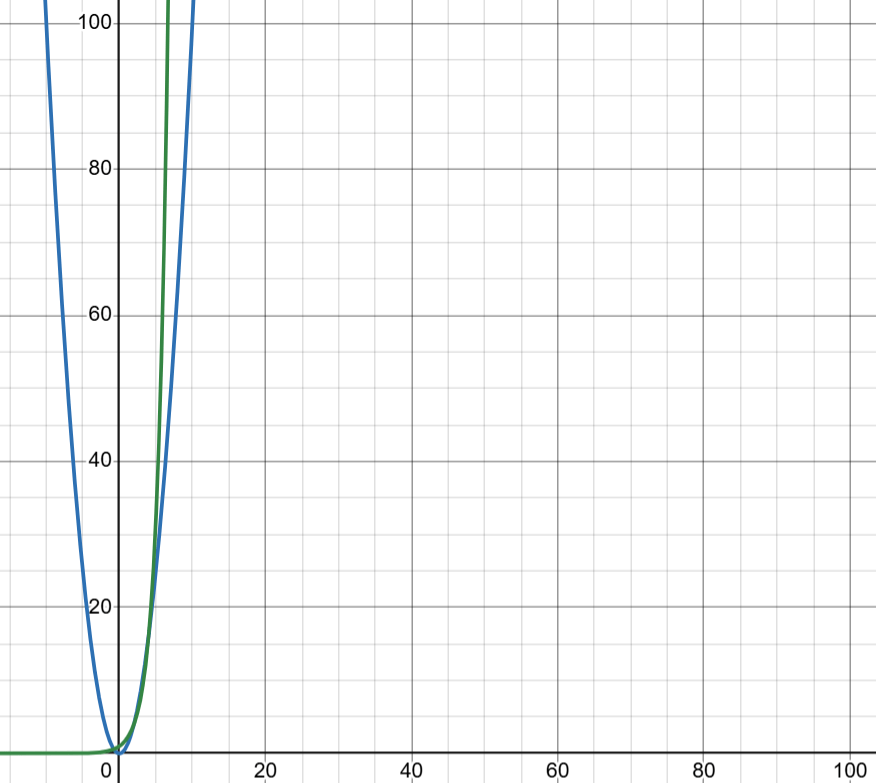
常見的六種時間複雜度與演算法
O(1)：陣列讀取
O(n)：簡易搜尋(一層迴圈)
O(log n)：二分搜尋
O(nlogn)：合併排序
O(n²)：選擇排序(兩層迴圈)
O(2^n)：費波那契數列
時間複雜度
空間複雜度
先來看看維基百科的定義：
蛤？就這樣？
空間複雜度
暫存空間
輸入空間
輸出空間
空間複雜度統計範圍
空間複雜度
注意事項：
1.大部分的原始型別（booleans、numbers、undefined、null）都是固定的空間
2.Strings 字串則是 O(n) space，這裡的 n 則是字串長度
3.物件型別的陣列與物件也是 O(n) space，n 則是陣列的長度或是物件的 key 數量
空間複雜度
S(n)=8=O(1)
void f1(int n){
int i;
while(i<=n){
i++;
}
}void f2(int n){
int i;
int f[n];
//省略程式碼
}S(n)=4n+8=O(n)
空間複雜度
void f3(int n){
int i;
int f[n];
int g[n][n];
//省略程式碼
}S(n)=n^2+n+8=O(n^2)
空間複雜度
S(n)=O(n)
void f1(int n){
int i;
while(i<=n){
i++;
}
}
int main(){
f1(5);
}空間複雜度
其實兩者概念都差不多這樣
實際寫程式的時候注意一下就好
程式優化
ios::sync_with_stdio(0);
cin.tie(0);解除cin,cout跟c語言的綁定
緩衝區每次調用都需要刷新
解除後就可以加快執行速率了
APCS
準備好被一些APCS 3,4題的解題概念轟炸吧！
給定一個長度為 L的林場，裡面種有 N棵樹，樹木依序排列。每棵樹的位置為 x，高度為 h。砍樹需遵守以下規則：
-
樹可以向左或向右倒下。
-
倒下的範圍不能超出林場邊界。
-
倒下的範圍內不能壓到尚未砍除的樹（僅接觸端點不算壓到）。
向左倒下的範圍為 [x−h,x]，向右倒下的範圍為 [x,x+h]。
依次砍除符合條件的樹木並移除，直到無法再砍除樹木為止。
最終能砍除的樹木數量是固定的，與砍樹順序無關。
輸入說明
第一行為正整數 N 及 L，代表樹的數量與林場右邊界的座標。N≤10^5，L≤10^9 。
第二行有 N 個正整數從小到大依序代表這 N 棵樹的座標，
所有座標不超過 L。
第三行有 N 個正整數依序代表樹的高度，都不超過 10^9。
輸出說明
輸出共有兩行，第一行輸出能被砍除之樹木數量，第二行輸出能被砍除之樹木中最高的高度，如果無法砍除任何一棵樹，則最高高度輸出 0。
輸入範例1
6 140
10 30 50 70 100 125
30 15 55 10 55 25
輸出範例1
4
30
我們藉著測資來看看這題
6 140
10 30 50 70 100 125
30 15 55 10 55 25
140的長度，種6顆
6 140
10 30 50 70 100 125
30 15 55 10 55 25
上面是x
下面是h
6 140
10 30 50 70 100 125
30 15 55 10 55 25
先把邊界設定好
total[0]
total[N+1]
x=0
h=1e9+1
x=L
h=1e9+1
6 140
10 30 50 70 100 125
30 15 55 10 55 25
10
30
6 140
10 30 50 70 100 125
30 15 55 10 55 25
10
30
30
15
6 140
10 30 50 70 100 125
30 15 55 10 55 25
30
20>15
15
cnt=1 max=15
6 140
10 30 50 70 100 125
30 15 55 10 55 25
30
50
55
10
6 140
10 30 50 70 100 125
30 15 55 10 55 25
30<40
55
cnt=2 max=30
6 140
10 30 50 70 100 125
30 15 55 10 55 25
50
55
10
70
6 140
10 30 50 70 100 125
30 15 55 10 55 25
50
55
10<20
cnt=3 max=30
6 140
10 30 50 70 100 125
30 15 55 10 55 25
50
55
100
55
6 140
10 30 50 70 100 125
30 15 55 10 55 25
50
55
100
55
25
125
6 140
10 30 50 70 100 125
30 15 55 10 55 25
50
55
55
cnt=4 max=30
25=25
輸出範例：
4 30
50
55
55
cnt=4 max=30
100
這題是用什麼演算法？
貪婪演算法
#include <bits/stdc++.h>
using namespace std;
struct tree{
int x;
int h;
};
tree total[100005];
stack<tree> st;
int main()
{
int N,L,mx,cnt;
while(cin>>N>>L){
mx=0;
cnt=0;
while(!st.empty()) st.pop();//先清空
for(int i=1;i<N+1;i++) cin>>total[i].x;
for(int i=1;i<N+1;i++) cin>>total[i].h;
total[0].x=0;
total[0].h=1e9+1;
total[N+1].h=1e9+1;
total[N+1].x=L;
st.push(total[0]);//加入一個永遠無法移除的樹
for(int i=1;i<N+2;i++){
while((st.top().x+st.top().h)<=total[i].x){ //右倒
cnt++;
mx=max(mx,st.top().h);
st.pop();
}
if(total[i].x-total[i].h>=st.top().x){
cnt++;
mx=max(mx,total[i].h);
}
else{
st.push(total[i]);
}//不能左倒就加入st
}
cout<<cnt<<endl;
cout<<mx<<endl;
}
}
看題目之前，我們先來了解什麼是約瑟夫問題
堆，這是數學版魷魚遊戲
約瑟夫問題(Josephus problem)
公元1世紀，約瑟夫和他的朋友以及其他猶太反抗者一起被羅馬軍隊包圍在洞穴中。為了不被俘虜，他們決定集體自殺。但約瑟夫並不願意真的自殺，於是他迅速提出了一個計劃。
他們所有人站成一個圈，並從某個點開始數數。每數到第2個人，這個人就必須自殺，然後從下一個活著的人重新開始數。約瑟夫迅速計算出他應該站在哪個位置，確保他是最後一個留下來的人。
約瑟夫問題(Josephus problem)
約瑟夫帶了40名士兵，他究竟選擇了哪個位置站呢？
約瑟夫問題(Josephus problem)
先看看6人的情況
1
2
3
4
5
6
約瑟夫問題(Josephus problem)
先看看6人的情況
1
2
3
4
5
6
約瑟夫問題(Josephus problem)
先看看6人的情況
1
2
3
4
5
6
約瑟夫問題(Josephus problem)
先看看6人的情況
1
2
3
4
5
6
約瑟夫問題(Josephus problem)
先看看6人的情況
1
2
3
4
5
6
約瑟夫問題(Josephus problem)
先看看6人的情況
1
2
3
4
5
6
約瑟夫問題(Josephus problem)
5號位置存活下來
1
2
3
4
5
6
約瑟夫問題(Josephus problem)
整理狀況
N是人數，f是生存者位置
| N | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| f | 1 | 1 | 3 | 1 | 3 | 5 | 7 | 1 |
| N | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| f | 3 | 5 | 7 | 9 | 11 | 13 | 15 | 1 |
有發現什麼規律嗎？
f都是奇數
約瑟夫問題(Josephus problem)
| N | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| f | 1 | 1 | 3 | 1 | 3 | 5 | 7 | 1 |
| N | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| f | 3 | 5 | 7 | 9 | 11 | 13 | 15 | 1 |
N=2^a,f=1
約瑟夫問題(Josephus problem)
| N | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| f | 1 | 1 | 3 | 1 | 3 | 5 | 7 | 1 |
| N | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| f | 3 | 5 | 7 | 9 | 11 | 13 | 15 | 1 |
N=2^a+b,f=2b+1,
(b<2^a)
約瑟夫問題(Josephus problem)
回到最初的問題，約瑟夫和他的40名士兵圍圈，他該站哪裡？
N=41=32+9,f=18+1=19
約瑟夫問題(Josephus problem)
接下來我們來找一般通式，假設每3人殺一個
1
2
3
4
5
6
約瑟夫問題(Josephus problem)
1
2
3
4
5
6
重新編號
4
5
x
1
2
3
1+3=4,2+3=5...
約瑟夫問題(Josephus problem)
f(N,k)=(N-1,k)+k
其實6個人的生存者和5個人的生存者是同個人，
我們只是換了編號而已
*注意：如果結果>N，就要減去N，才能與左式相等
N個人圍成一圈
每次到第M個人就會爆炸
這枚炸彈只會爆K次，在第 K次爆炸後，遊戲即停止，而此時在第K個淘汰者的下一位遊戲者被稱為幸運者
#include<bits/stdc++.h>
using namespace std;
int n,m,k;
int main(){
cin>>n>>m>>k;
int tmp=0;
for(int i=n-k+1;i<=n;i++)tmp=(tmp+m)%i;
//%i->mod
//計算每輪的淘汰位置
cout<<tmp+1<<"\n";
//從0開始算，最後要加一
}
約瑟夫問題解法
#include <iostream>
#include <vector>
using namespace std;
int main() {
int n, m, k, now;
vector<int> p;
while (cin >> n >> m >> k) {
p.clear();
for (int i = 1; i <= n; i++) {
p.push_back(i);
}
now = 0;
for (int i = 0; i<k; i++) {
now = (now + m - 1) % p.size();
p.erase(p.begin() + now);//刪除被炸的人
}
now = now%p.size();
cout << p[now]<<endl;
}
}直接模擬的解法
參考資料點圖片->
輸入為 m×n 大小的的陣列，每一格是一個介於 -100 與 100 之間的整數，表示經過這格可以累積的經驗值。
你可以從最上面一排任何一個位置開始，在最下面一排任何一個位置結束。
過程中每一步可以選擇往左、往右或往下走，但不能走回已經經過的位置。
請你算出最多可以獲得的經驗值總和(可能是負數)。
這好像有點熟悉，是什麼演算法呢？
dp 動態規劃
這題與一般dp不同的是允許下左右任意方向任意位置加
1
2
3
4
5
-6
7
-8
-9
10
11
12
10
9
7
10
5
-6
7
-8
-9
10
11
12
1+2+3+4
2+3+4
3+4
1+2+3+4
10
9
7
10
15
9
16
8
-9
10
11
12
10+5
15-6
9+7
16-8
10
9
7
10
15
9
16
8
32
41
31
42
10+11+12+8-9
11+12+8+10
11+12+8
9+10+11+12
簡單來說
我們要分開考慮下、右、左的狀況
左邊來的計算一次，然後判斷與上方來的和的大小
右邊來的計算一次，然後判斷與上方來的和的大小
比較哪個方式的值最大，最後檢查最後一行的max
#include<bits/stdc++.h>
using namespace std;
int m,n,dp[50][10000]={0};//所有的點
int main(){
cin>>m>>n;
for(int i=1;i<=m;i++){
int a[10000],l[10000]={0},r[10000]={0};//兩邊來的最大值
for(int j=1;j<=n;j++){
cin>>a[j];
}
for(int j=1;j<=n;j++){
if(j==1) l[j]=dp[i-1][j]+a[j];
else l[j]=max(dp[i-1][j],l[j-1])+a[j];
}
//算左邊過來的最大值
//第一步一定從上往下來的，再往右走，判斷哪邊來的比較大
for(int j=n;j>=1;j--){
if(j==n) r[j]=dp[i-1][j]+a[j];
else r[j]=max(dp[i-1][j],r[j+1])+a[j];
}
//算右邊過來的最大值
//第一步一定從上往下來的，再往左走，判斷哪邊來的比較大
for(int j=1;j<=n;j++){
dp[i][j]=max(l[j],r[j]);
}
//判斷左邊過來的比較大還是右邊來的
}
int ans=dp[0][0];
for(int j=1;j<=n;j++){
ans=max(ans,dp[m][j]);
}
//找最後一行的最大值
cout<<ans<<endl;
}
參考資料點圖片->
1
2
w(1)=1,w(2)=2,f(1)=3,f(2)=4
1
2
w(1)=1,w(2)=2,f(1)=3,f(2)=4
花費能量：0
1
2
w(1)=1,w(2)=2,f(1)=3,f(2)=4
花費能量：1*4
1
2
w(1)=1,w(2)=2,f(1)=3,f(2)=4
1
2
w(1)=1,w(2)=2,f(1)=3,f(2)=4
花費能量：0
1
2
w(1)=1,w(2)=2,f(1)=3,f(2)=4
花費能量：2*3
考慮任兩個物品間的上下擺放關係：
物品 p1 = [w1, f1]；物品 p2 = [w2, f2]
p1 放在 p2 的上方：w1 * f2
p2 放在 p1 的上方：w2 * f1
物品兩兩比較後，依最省力的方式排序。
*這題使用貪心就可以解了
#include <bits/stdc++.h>
using namespace std;
struct box{
int w,f;
};
bool cmp (box a,box b){
return (a.w*b.f<a.f*b.w);
}
int main(){
int n;
while(cin>>n){
struct box b[n];
for(int i=0;i<n;i++) cin>> b[i].w;
for(int i=0;i<n;i++) cin>> b[i].f;
sort(b,b+n,cmp);
long long int ans=0,sum=b[0].w;
for(int i=1;i<n;i++){
ans+=sum*b[i].f;
sum+=b[i].w;
}
cout<<ans<<endl;
}
}參考資料點圖片->
下課後記得要多練習喔！
AP325
By 愛錢成癡，嗜賭成癮
