Big Data Cosmology meets AI

IAIFI Fellow

Carol Cuesta-Lazaro

 

The Ohio State University - 15 April 2024

Video Credit: N-body simulation Francisco Villaescusa-Navarro

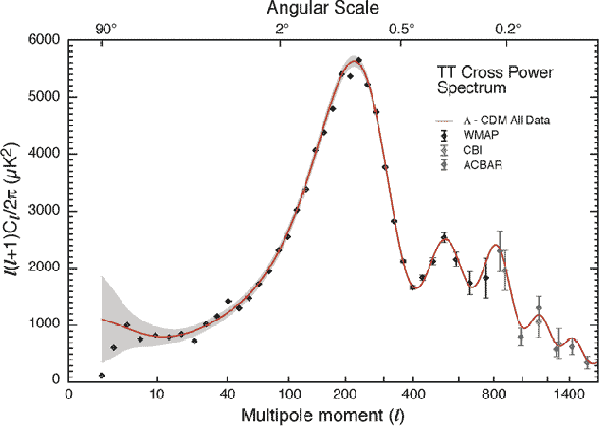
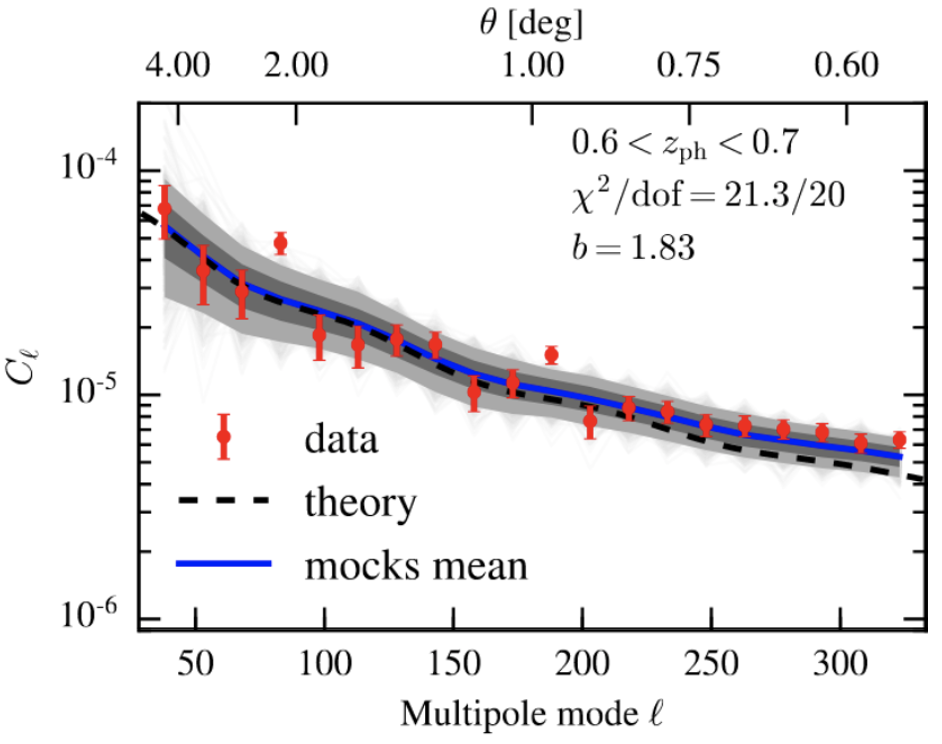
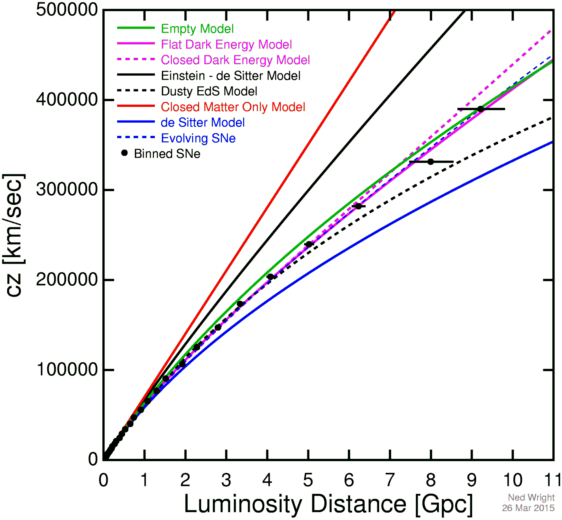
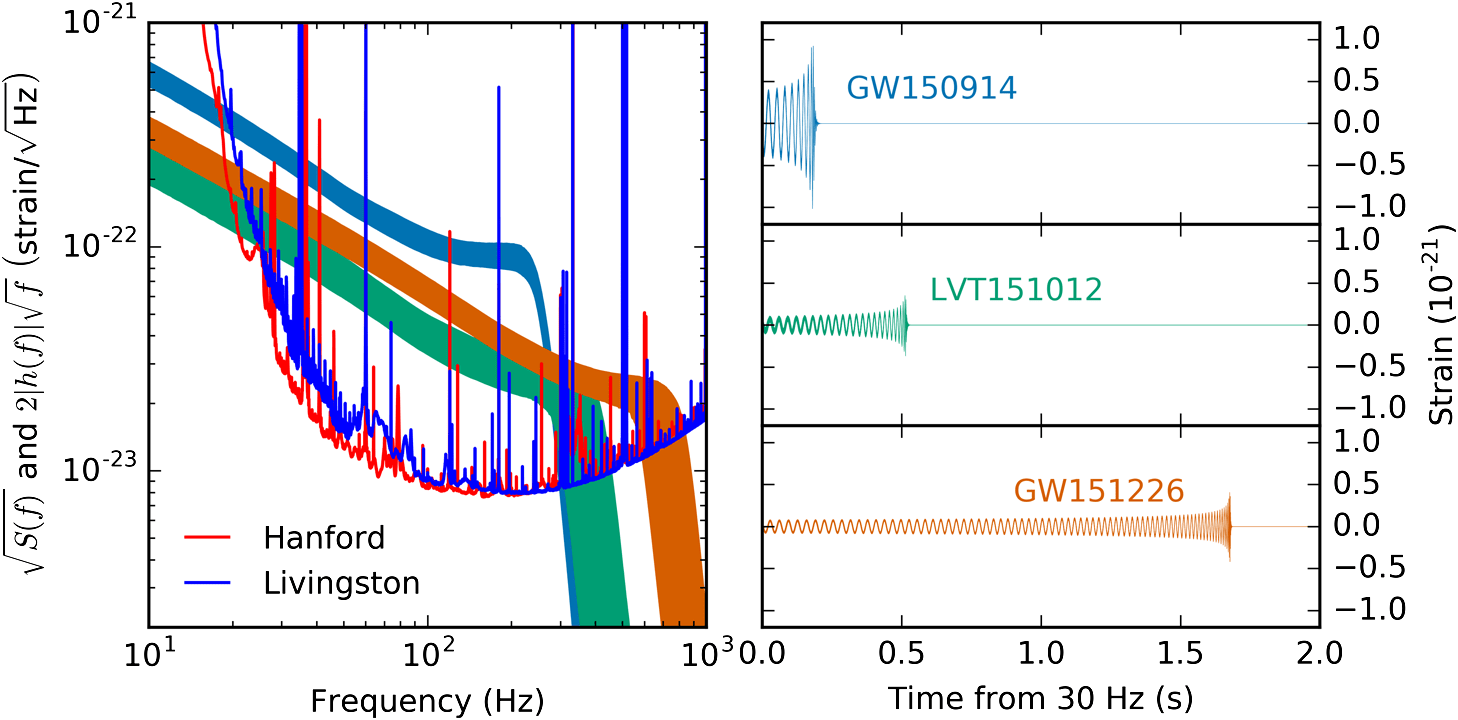
The era of Big Data Cosmology

1-Dimensional

Machine Learning

Secondary anisotropies

Galaxy formation

Intrinsic alignments

Dust

xAstrophysics

DESI, DESI-II, Spec-S5

Euclid

LSST

Simons Observatory

CMB-S4

Ligo

Einstein

LSST

Early Universe Inflation

{\delta_\mathrm{Initial}}

Late Universe

Energy and matter content

Evolution

{\delta_\mathrm{Final}}
\color{darkgray}{\Omega_m}

Dark matter

Dark energy

\color{darkgreen}{w_0, w_a}
\color{darkolive}{H_0}

Hubble Constant

\color{darkred}{\Omega_b}
\color{darkblue}{\sum m_\nu}

Baryons

Neutrino masses

\color{purple}{f_\mathrm{NL}}
\color{darkorange}{n_s}

Non-Gaussianity

Tilt power spectrum

Hubble tension

Beyond the Standard Model

Multifield Inflation

Dark Matter Reconstruction

2
3

Hybrid ML - Physics Simulators

1

Cosmological (field level) Inference for Galaxy Surveys

DESI

Fast Simulators

High dimensional inference

Modelling priors

Uncertainty quantification

arXiv:2403.10648
arXiv:2402.13310
arXiv:2309.09337

DESI: Dark Energy Spectroscopic Instrument

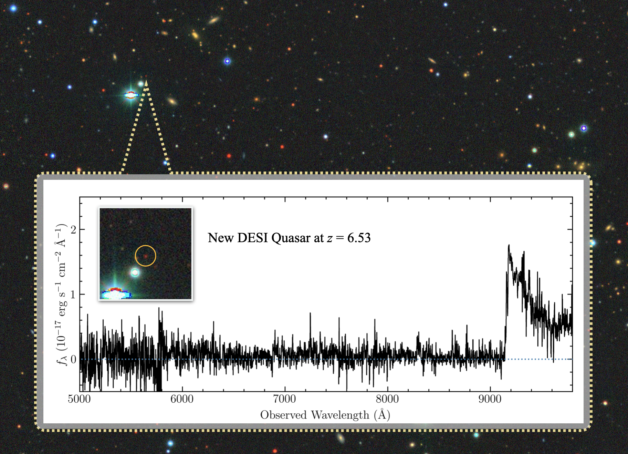
~40 Million spectra!

(Image Credit: Jinyi Yang, Steward Observatory/University of Arizona)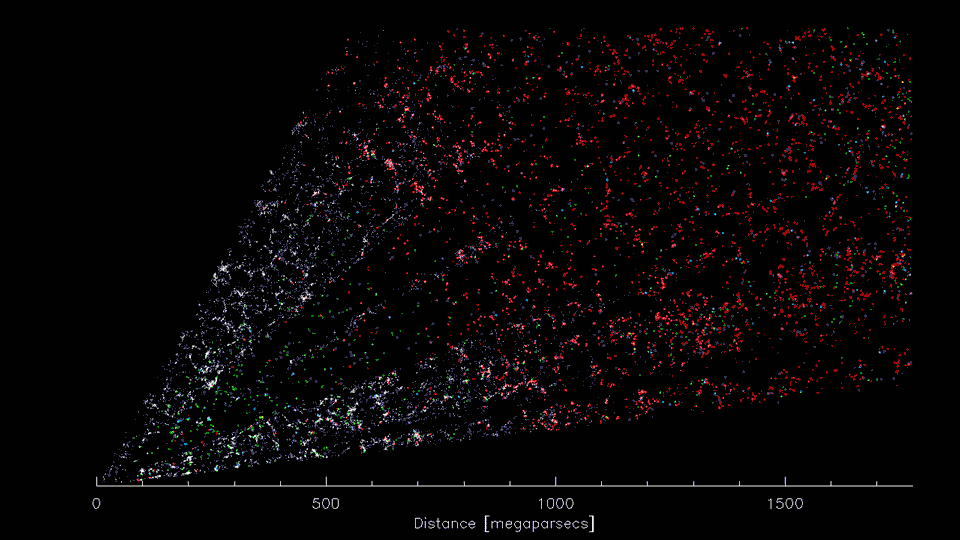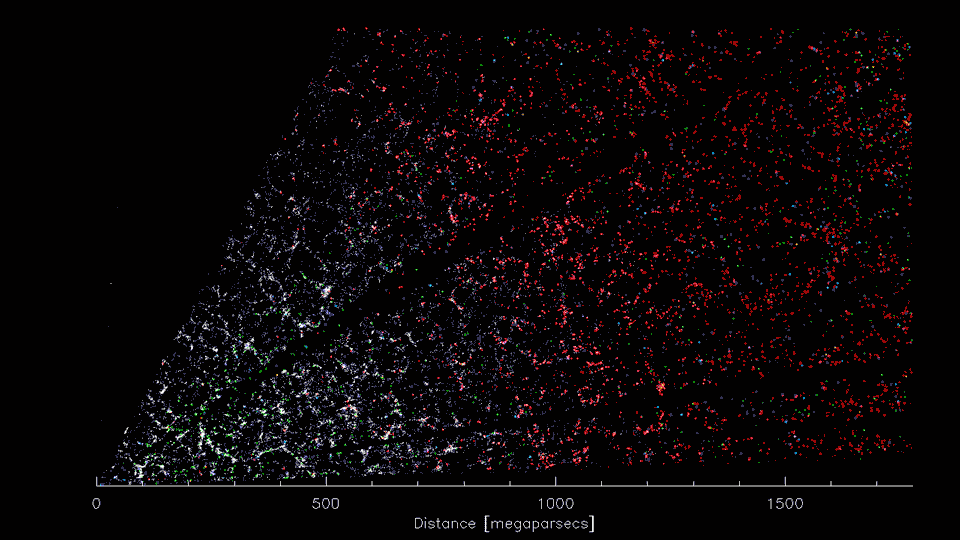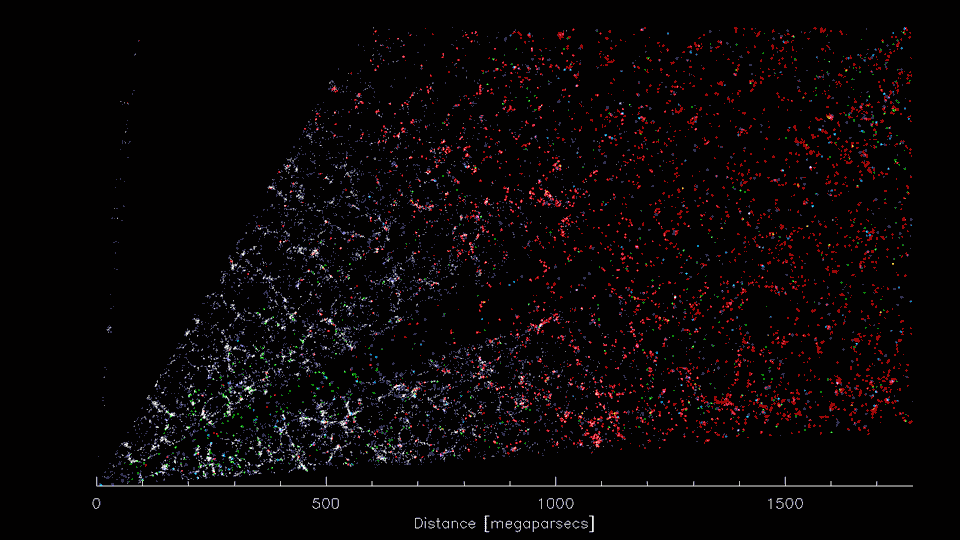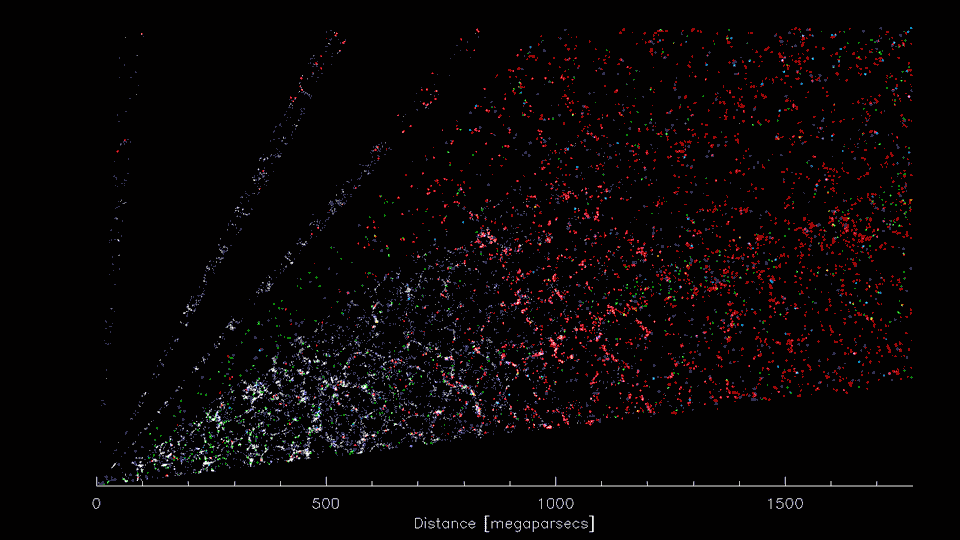

(Image Credit: D. Schlegel/Berkeley Lab using data from DESI)

High dimensional data 

x

Unknown

p(x|\mathcal{C})

Simple summary statistic 

s
p(s|\mathcal{C})

estimated with Perturbation Theory

Probability pair of galaxy

Pair separation

\theta

Forward Model

Parameters

Observable

x

Likelihood

p(\mathcal{\theta}|x)

Simulator

+ MCMC hammer

\color{darkgray}{\Omega_m}, \color{darkgreen}{w_0, w_a},\color{purple}{f_\mathrm{NL}}\, ...

Dark matter

Dark energy

Inflation

Perturbation Theory

Pen and paper

p(x|\mathcal{\theta})

+ Density Estimation

+ Sampler

p(\mathcal{\theta}|x) =
p(\theta) / p(x)

DESI

Initial conditions

\color{darkgray}{\Omega_m}, \color{darkgreen}{w_0, w_a},\color{purple}{f_\mathrm{NL}}\, ...

Dark matter

Dark energy

Inflation

\theta
+

A forward model samples the likelihood

\theta

Parameters

Observable

x

Observed galaxy pointcloud

Initial conditions

+
\color{darkgray}{\Omega_m}, \color{darkgreen}{w_0, w_a},\color{purple}{f_\mathrm{NL}}\, ...

DESI

Forward Model

Example: How far will Justin Fields throw?

def simulate_trajectory(
    velocity, 
    angle, 
    time_step=0.1, 
    g=9.8,
):
    z_velocity = np.random.normal(scale=2.)
    z_angle = np.random.normal(scale=2.)
    velocity  = velocity + z_velocity
    angle = angle + z_angle
    angle_rad = np.radians(angle)
    v_x = velocity * np.cos(angle_rad)
    v_y = velocity * np.sin(angle_rad)
    total_time = 2 * v_y / g
    times = np.arange(0, total_time, time_step)
    x = v_x * times
    y = v_y * times - 0.5 * g * times**2
    x_american = x * 1.09361
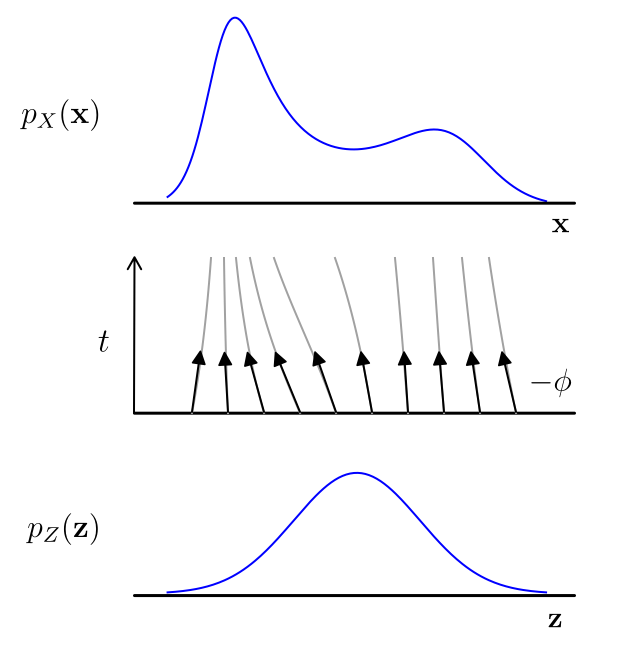
    return x_american, y, times
v \sim \mathcal{N} (23,2)
\phi \sim \mathcal{U} (30,45)

Sample Prior

Simulator

Latent variables z

x
p(x|\theta) = \int dz p(x,z|\theta)
x_\mathrm{simulator} \sim p(x|\theta)

Maximize the likelihood of the training samples

\hat \phi = \argmax \left[ \log p_\phi (x_\mathrm{train}) \right]

Model

p_\phi(x)

Training Samples

x_\mathrm{train}

Generate Novel Samples

Evaluate probabilities

Trained Model

p_\phi(x|\theta)

A 2D animation of a folk music band composed of anthropomorphic autumn leaves, each playing traditional bluegrass instruments, amidst a rustic forest setting dappled with the soft light of a harvest moon

Image credit: DALL·E 3

 

1024x1024

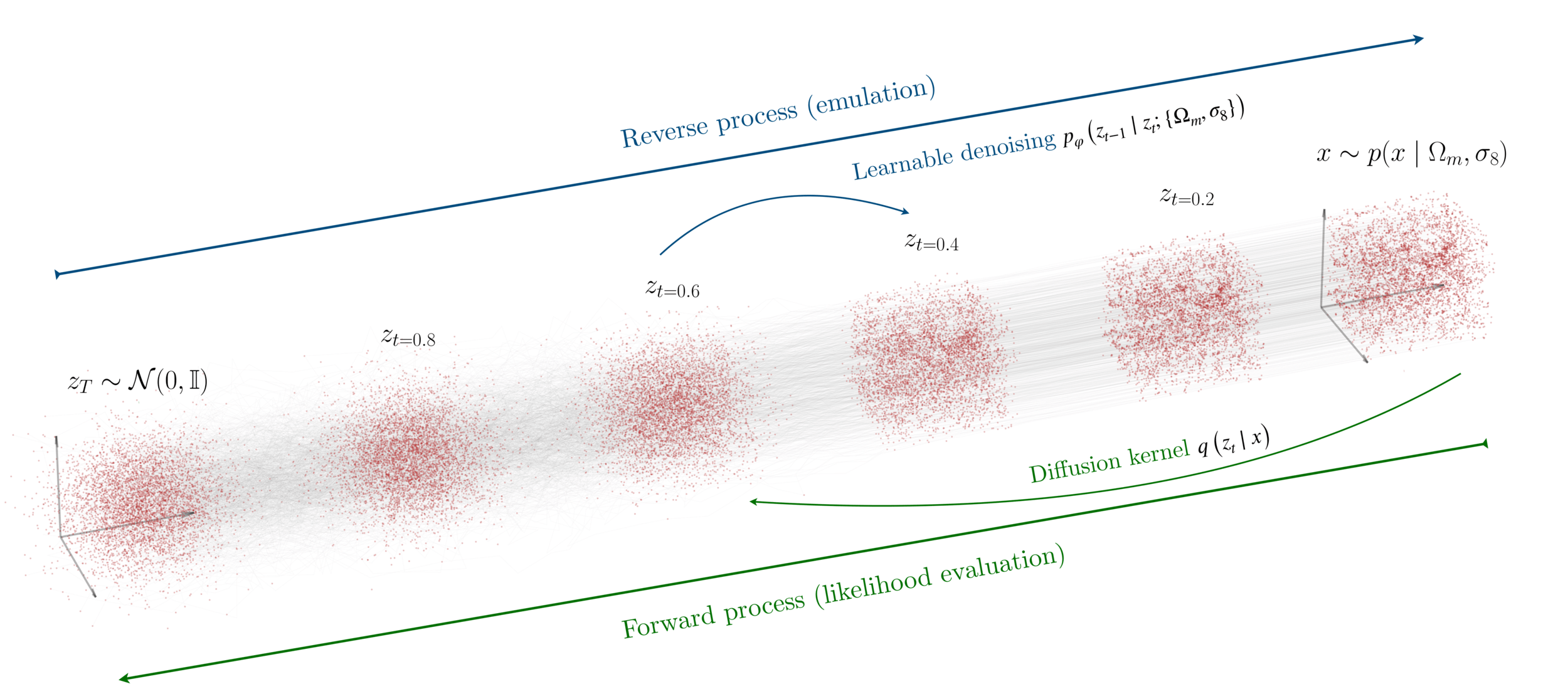
"A point cloud approach to generative modeling for galaxy surveys at the field level" 
Cuesta-Lazaro and Mishra-Sharma 

https://arxiv.org/abs/2311.17141

Base Distribution

Target Distribution

  • Sample
  • Evaluate

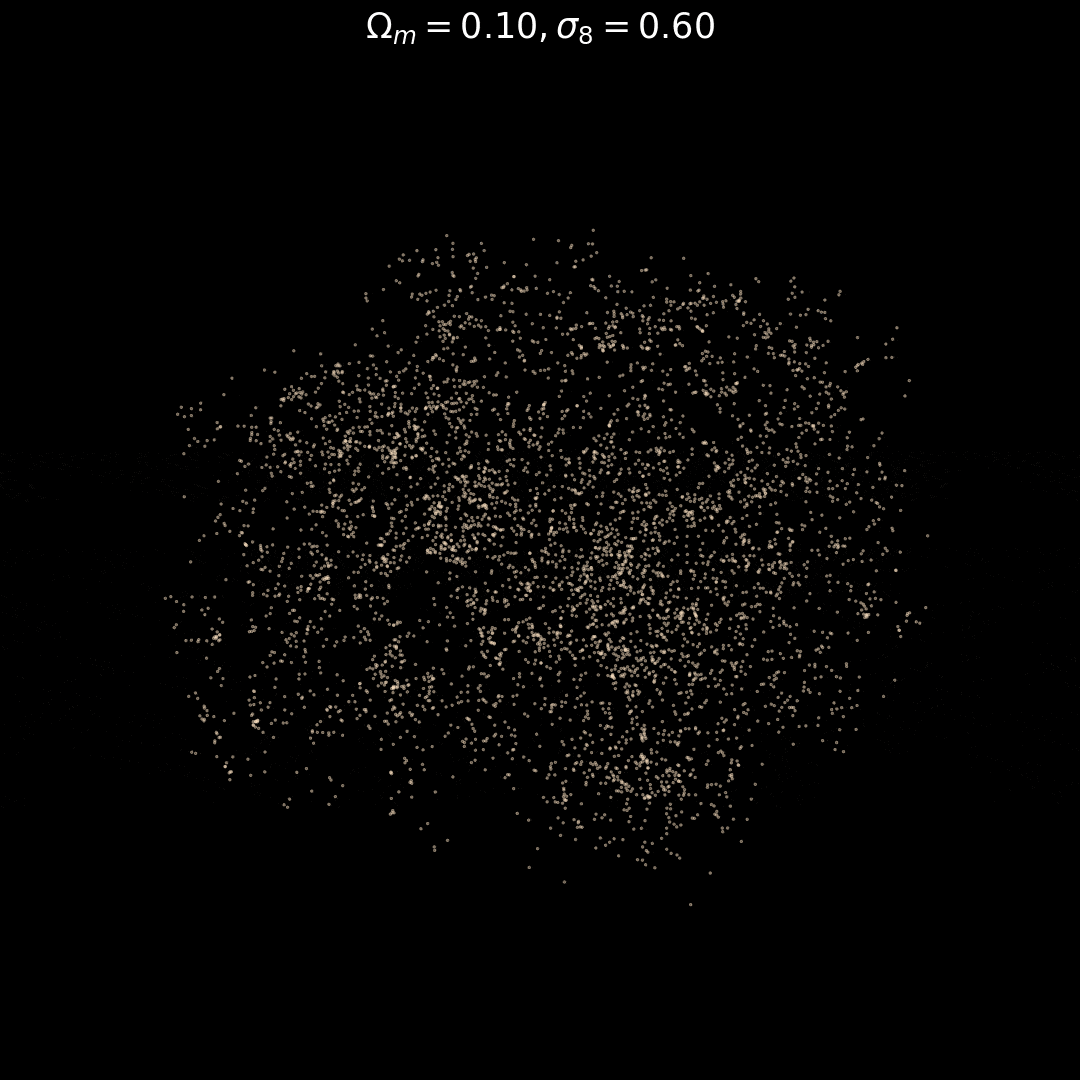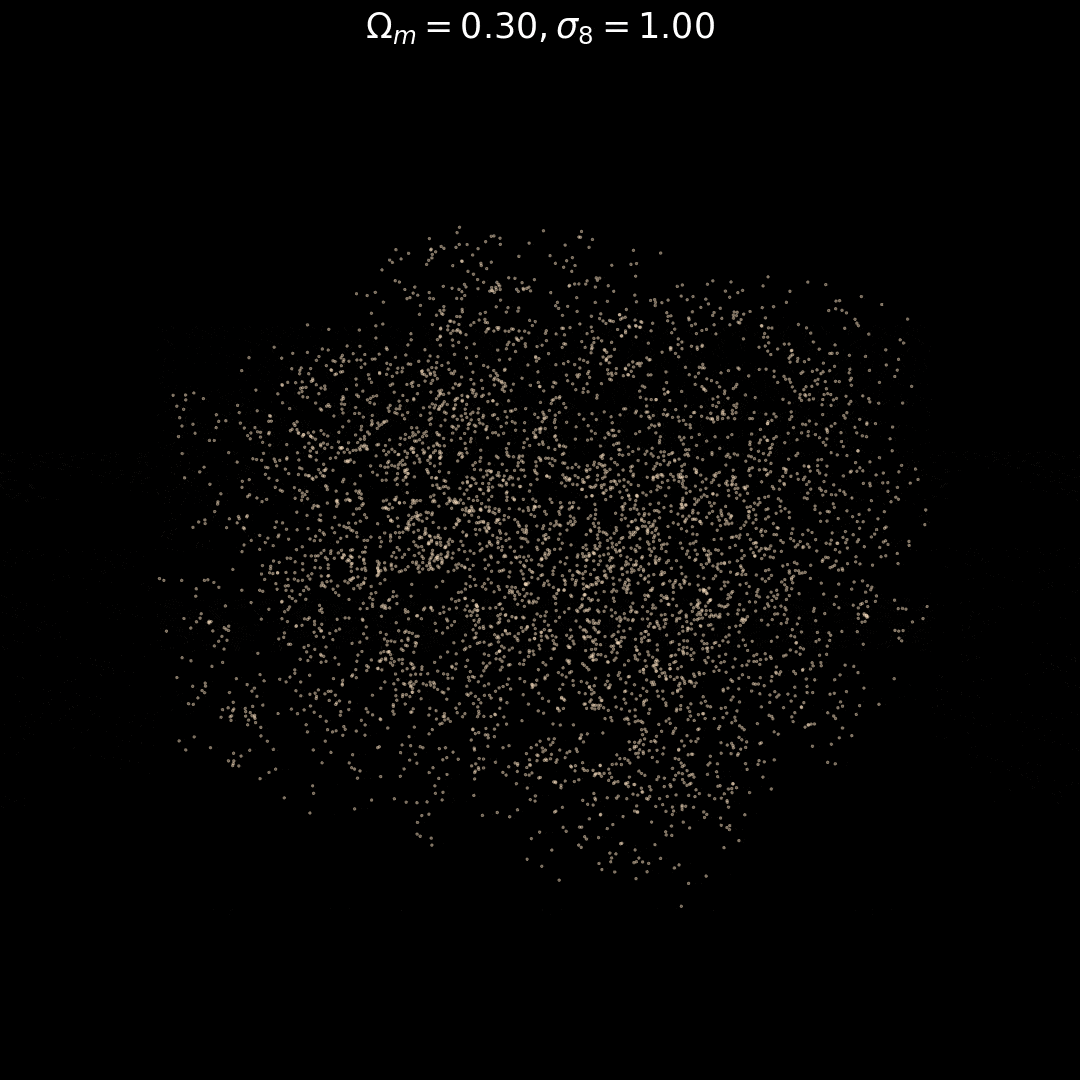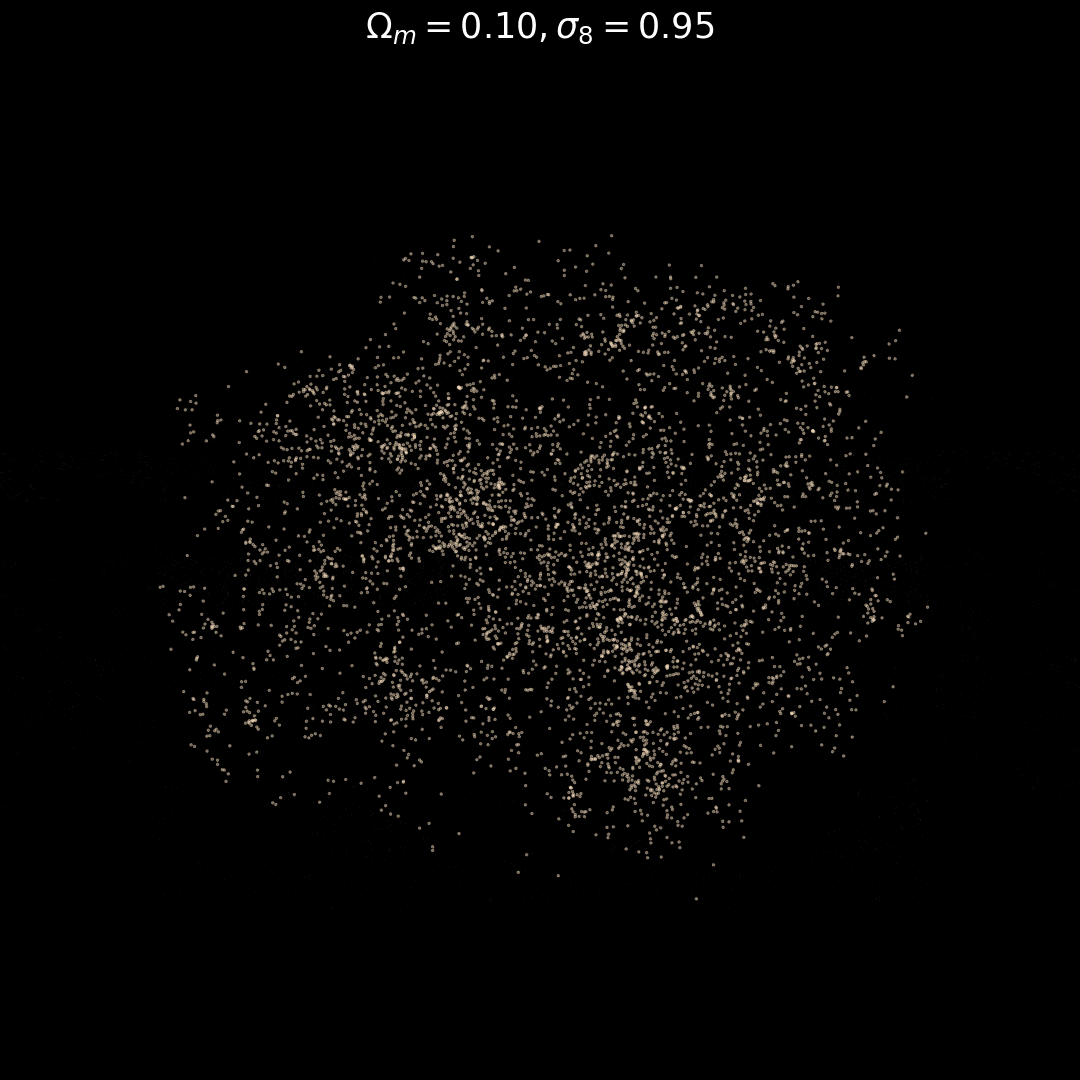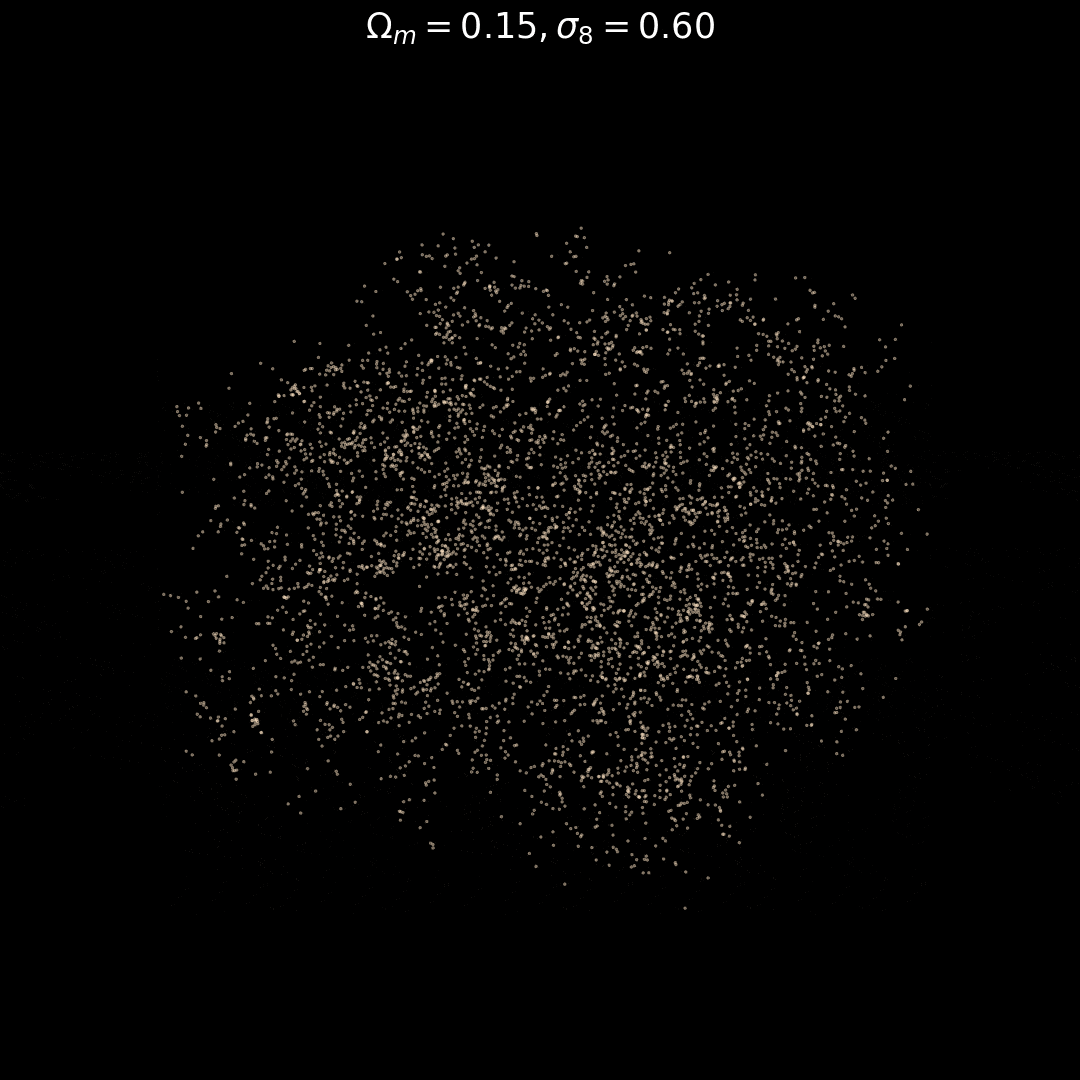
Fixed Initial Conditions

 Varying Cosmology

Mean pairwise

velocity

k Nearest neighbours

Pair separation

Pair separation

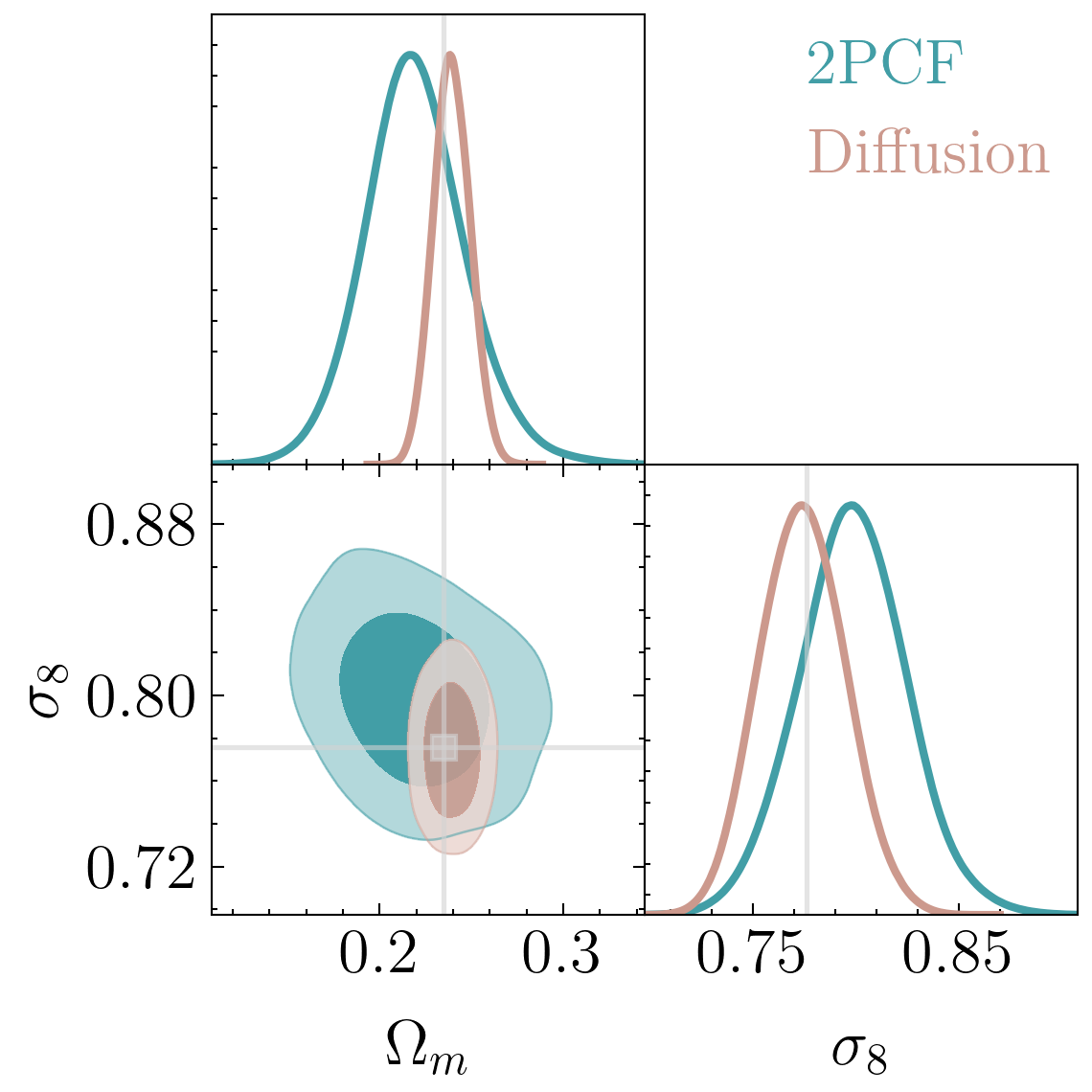
Trained on only 5000 positions!

https://arxiv.org/abs/2210.02747
https://arxiv.org/abs/2302.00482

Flow Matching

\frac{d x_t}{dt} = u_t(x_t)

Flow ODE

x_0
p(x_0)
p(x_1)
x_1
u_t
\frac{d p_t}{dt} = - \left(\nabla u_t p_t \right)(x_t)

Continuity Eq.

Random pairings (x0, x1)

Optimal Transport (x0, x1)

p_\phi(\delta_\mathrm{z=127}|\delta_\mathrm{z=0})

1 to Many:

https://arxiv.org/abs/2303.08797

ODE

SDE

x_0
x_1
x_t
x_t
x_0
x_1

Power Spectrum

Cross correlation

Small

Large

Scale (k)

Small

Large

Scale (k)

Small

Large

Scale (k)

Small

Large

Scale (k)

p_\phi(\rho_\mathrm{DM}|\rho_\mathrm{Galaxies})

1 to Many:

Stellar Mass distribution 

Dark Matter

 "Probabilistic Reconstruction of Dark Matter fields from galaxies"
Park, Ono, Mudur, Ni, Cuesta-Lazaro NeurIPS Machine Learning and the Physical Sciences

Victoria Ono

Core Park

Truth

Sampled

Observed

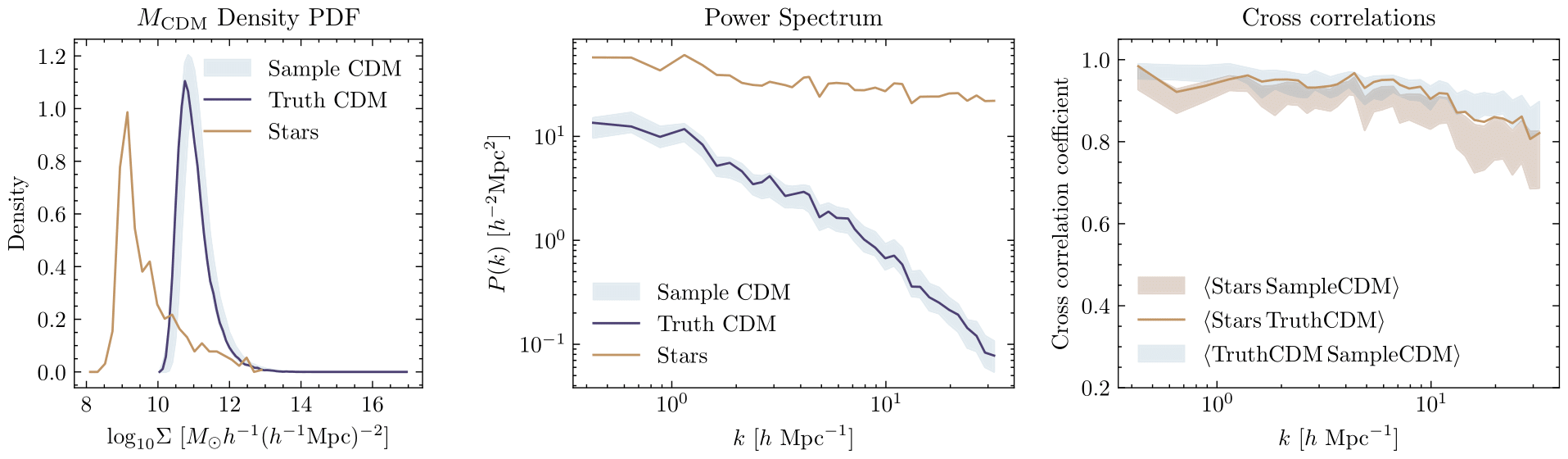
Small

Large

Scale (k)

Power Spectrum

PDF

log Mass

 ~ Gpc

pc

kpc

Mpc

Gpc

Video credit: Francisco Villaescusa-Navarro

Small

Large

\langle\mathrm{True}\,\,\mathrm{Pred}\rangle

In-Distribution

In-Distribution

In-Distribution

Out-of-Distribution

Out-of-Distribution

Out-of-Distribution

Out-of-Distribution

Out-of-Distribution

Out-of-Distribution

CAMELS

DESI LRG ~ 20 (Gpc/h)^3 

TNG-300

True DM

Sample DM

Small

Large

Scale (k)

Power Spectrum

PDF

log Mass

Can we run larger simulations? (DESI volumes)

At high resolution?

Faster?

All this works depends on simulations, but...

Thousands of them?

\frac{\mathrm{d} \mathbf{x}}{\mathrm{d} a } = \frac{1}{a^3 E(a)}\mathbf{v}
\frac{\mathrm{d} \mathbf{v}}{\mathrm{d} a } = \frac{1}{a^2 E(a)}\mathbf{F}(\mathbf{x},a)
\mathbf{F}(\mathbf{x},a) = \frac{3 \Omega_m}{2} \nabla \phi^\mathrm{PM}(\mathbf{x})

Gravitational evolution ODE

Particle-mesh

Particle-mesh

Full Nbody

\mathbf{F}_\theta(\mathbf{x},a) = \frac{3 \Omega_m}{2} \nabla \left[\phi^\mathrm{PM}(\mathbf{x}) + \phi^\mathrm{corr}_\theta(\mathbf{x}, a, \phi^\mathrm{PM}, \delta^\mathrm{PM}) \right]

Hybrid Simulator - on the fly

\frac{\mathrm{d} \mathbf{x}}{\mathrm{d} a } = \frac{1}{a^3 E(a)}\mathbf{v}
\frac{\mathrm{d} \mathbf{v}}{\mathrm{d} a } = \frac{1}{a^2 E(a)}\mathbf{F}(\mathbf{x},a)

Gravitational evolution ODE

Trained to match particle velocities and positions: DIFFERENTIABLE

Particle-mesh

Full Nbody

Hybrid ML-Simulator

"Nbodyify: Adaptive mesh corrections for PM simulations" Cuesta-Lazaro, Modi in preps
p_\phi(\delta_\mathrm{Nbody}|\delta_\mathrm{PM})

Hybrid subgrid models to bridge scales

High Res Sim

Springel and Hernquist 03

DESI

Building digital twins

Selections

Survey systematics

=

Robustness

Extract only information that is robust

across time

\mathrm{C} \cap \mathrm{A}
\mathrm{Cosmology}
\mathrm{Astrophysics}

Conclusions

1. There is a lot of information in galaxy surveys that ML methods can access

2. We can tackle high dimensional inference problems so far unatainable

3. Our ability to simulate will limit the amount of information we can extract

Hybrid simulators, forward models, robustness

Dark matter, Initial Conditions, let's get creative!

Field level inference

The Ohio State-Seminar2024

By carol cuesta

The Ohio State-Seminar2024

  • 132

More from carol cuesta