Enrique Paillas, Pauline Zarrouk, Yan-Chuan Cai, Will Percival, Sesh Nadathur, Mathilde Pinon, Arnaud de Mattia, Florian Beuler
Constraining ΛCDM with density split statistics
Carolina Cuesta-Lazaro
IAIFI fellow - MIT/CfA
arXiv:2209.04310
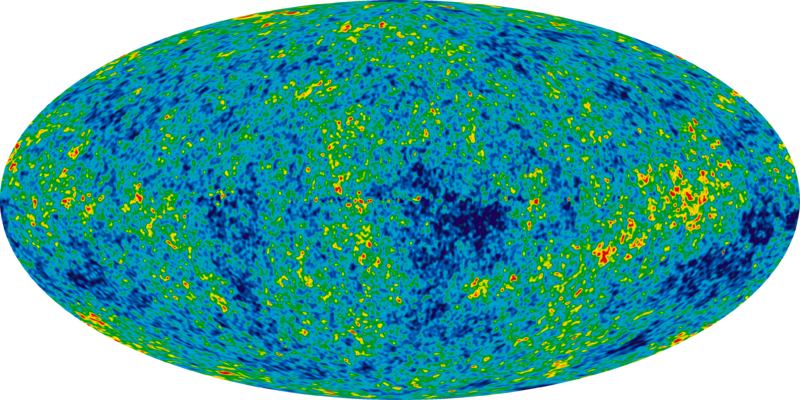
Early Universe
~linear
Gravity
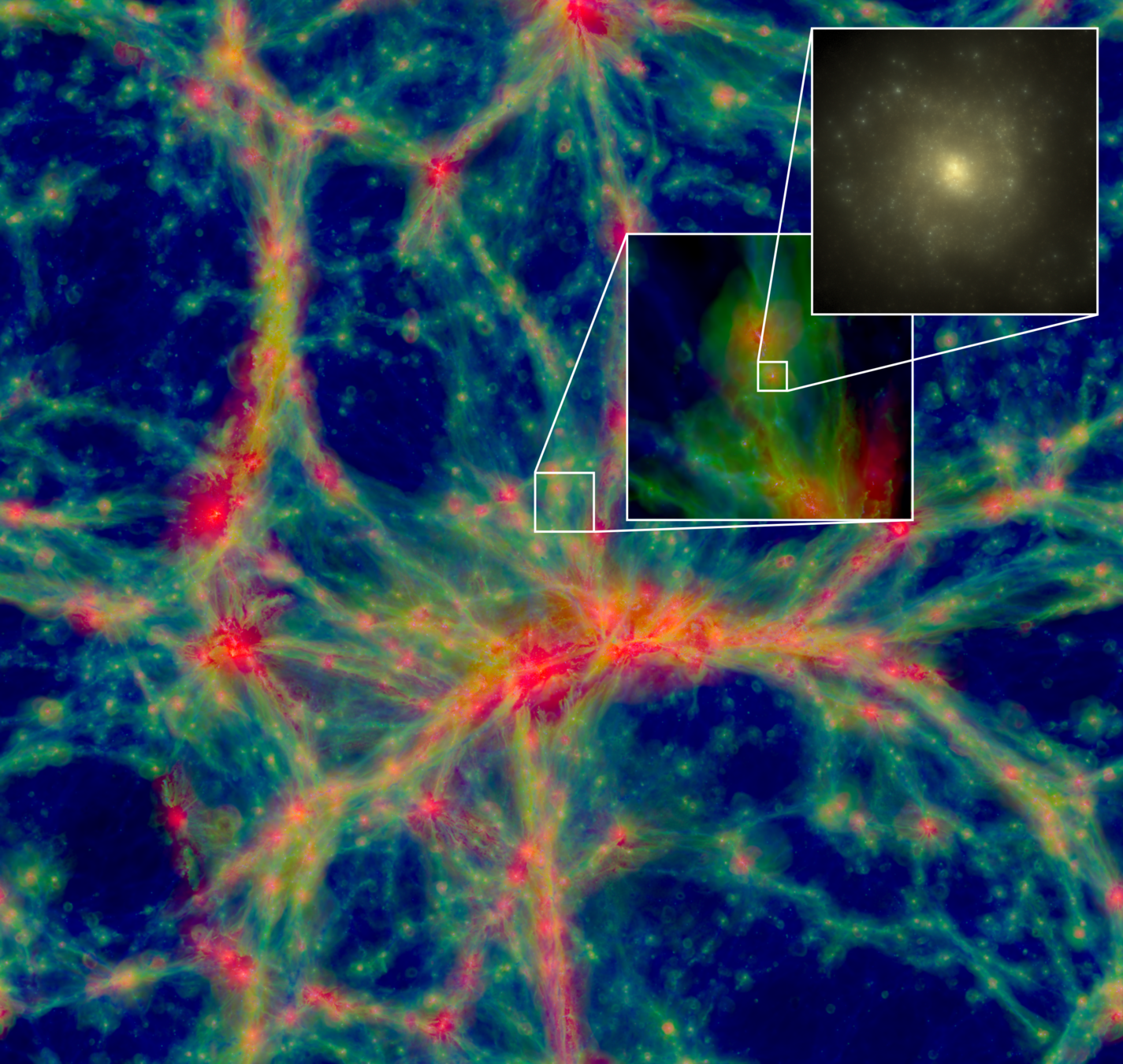
Late Universe
Non-linear
Credit: S. Codis+16
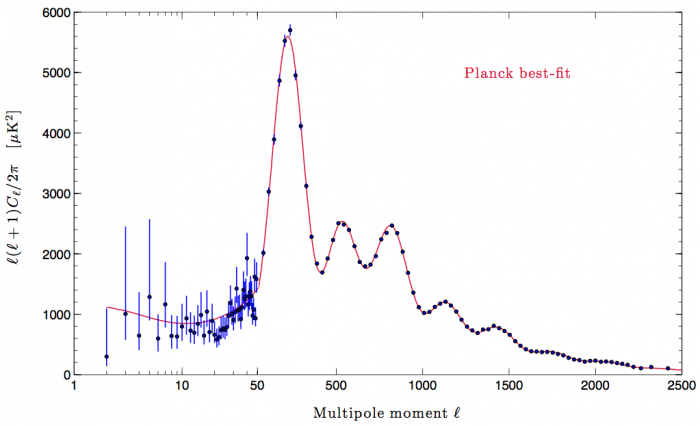
Non-Guassianity
Second moment not optimal
\delta = \frac{\rho - \bar{\rho}}{\bar{\rho}} << 1
\delta >> 1
\bar{\xi}(R_s)
R_s
1
1
1
2
2
4
5
5
5
3
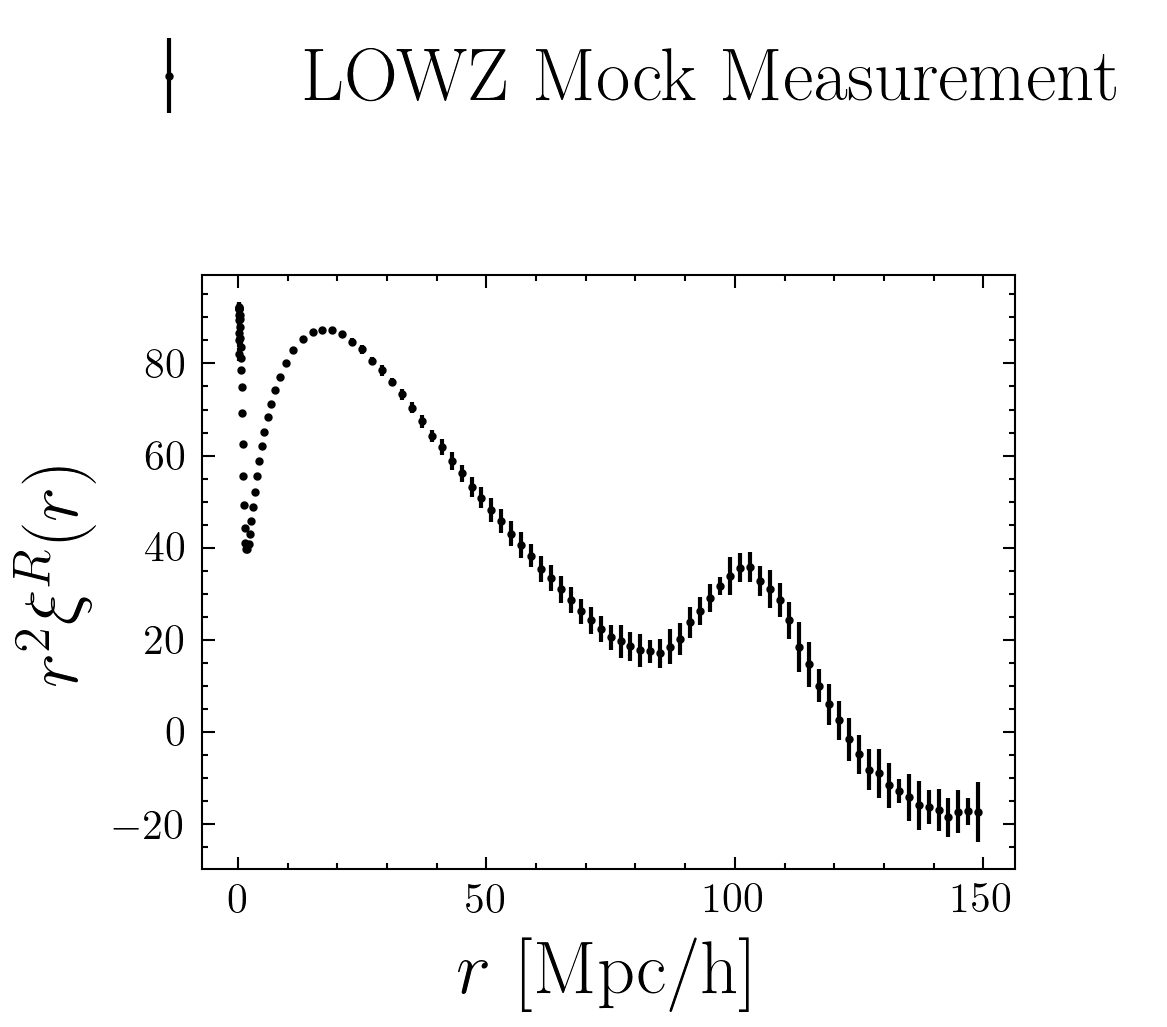
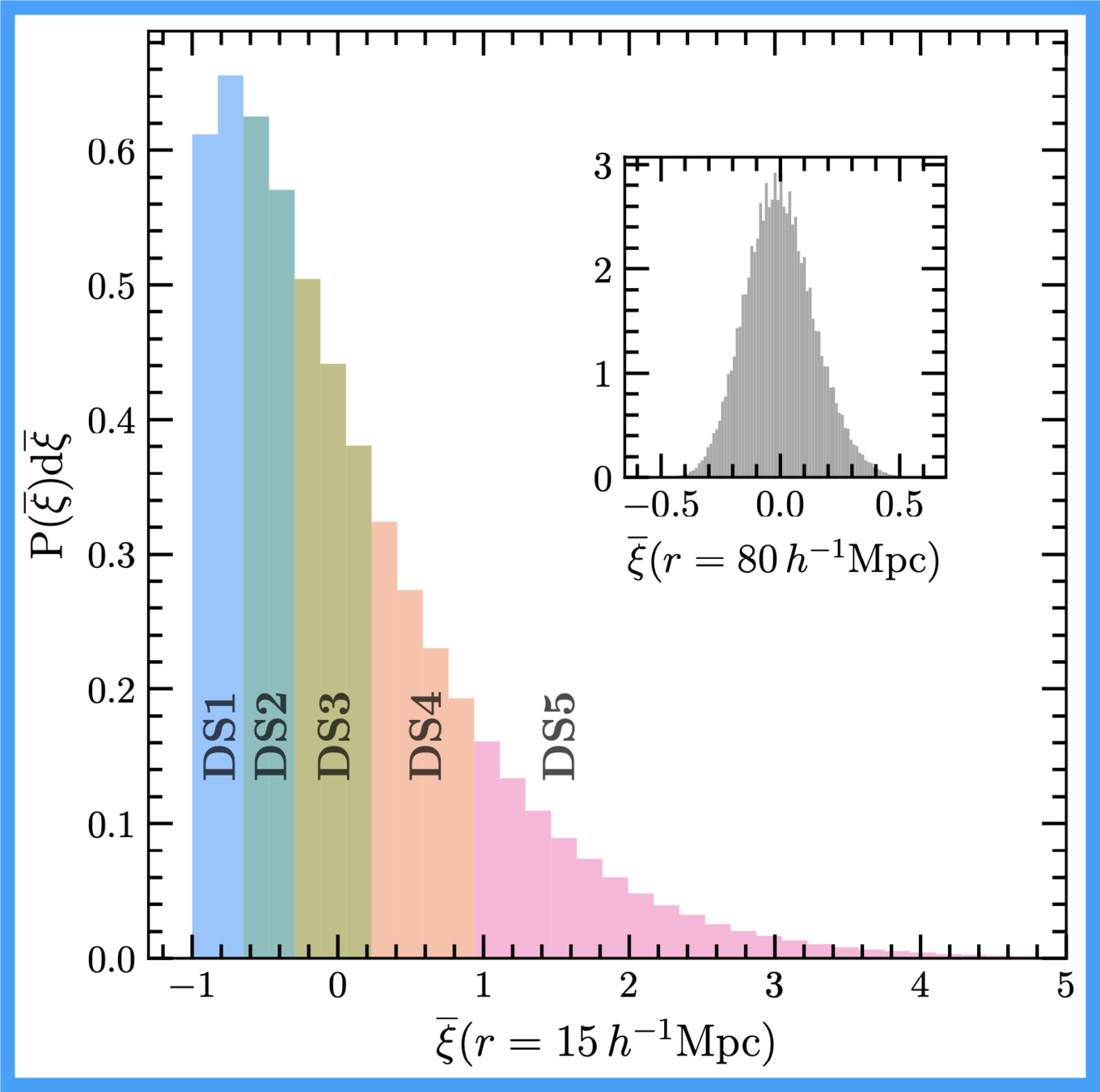
arxiv:1911.11158
1
1
1
2
2
4
5
5
5
3
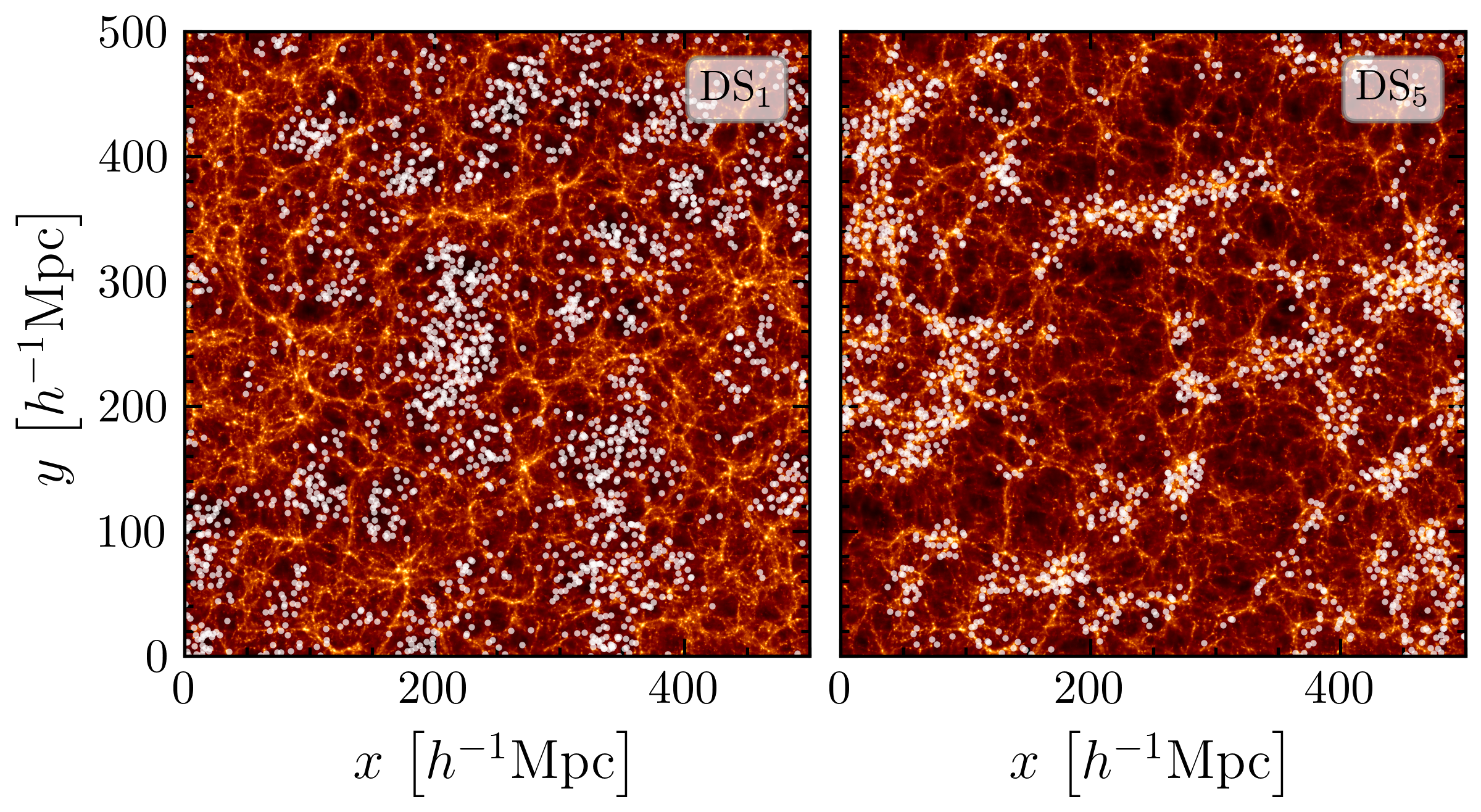
Autocorrelation
10
50
90
130
Cross-correlation with haloes
Monopole
Quadrupole
Voids
Clusters
10
50
90
130
s^2
s^2
F_{\alpha \beta} = \mathbb{E} \left[\frac{\partial^2 \ln \mathcal{L}(x|\theta)}{\partial \theta_i \partial \theta_j} \right] = \frac{\partial S}{\partial \theta_\alpha} C^{-1} \frac{\partial S}{\partial \theta_\beta}
\delta \theta_\alpha \geq \left( F^{-1} \right)_{\alpha \alpha}
\frac{\partial \log \mathcal{L}(x|\theta)} {\partial \theta} = 0
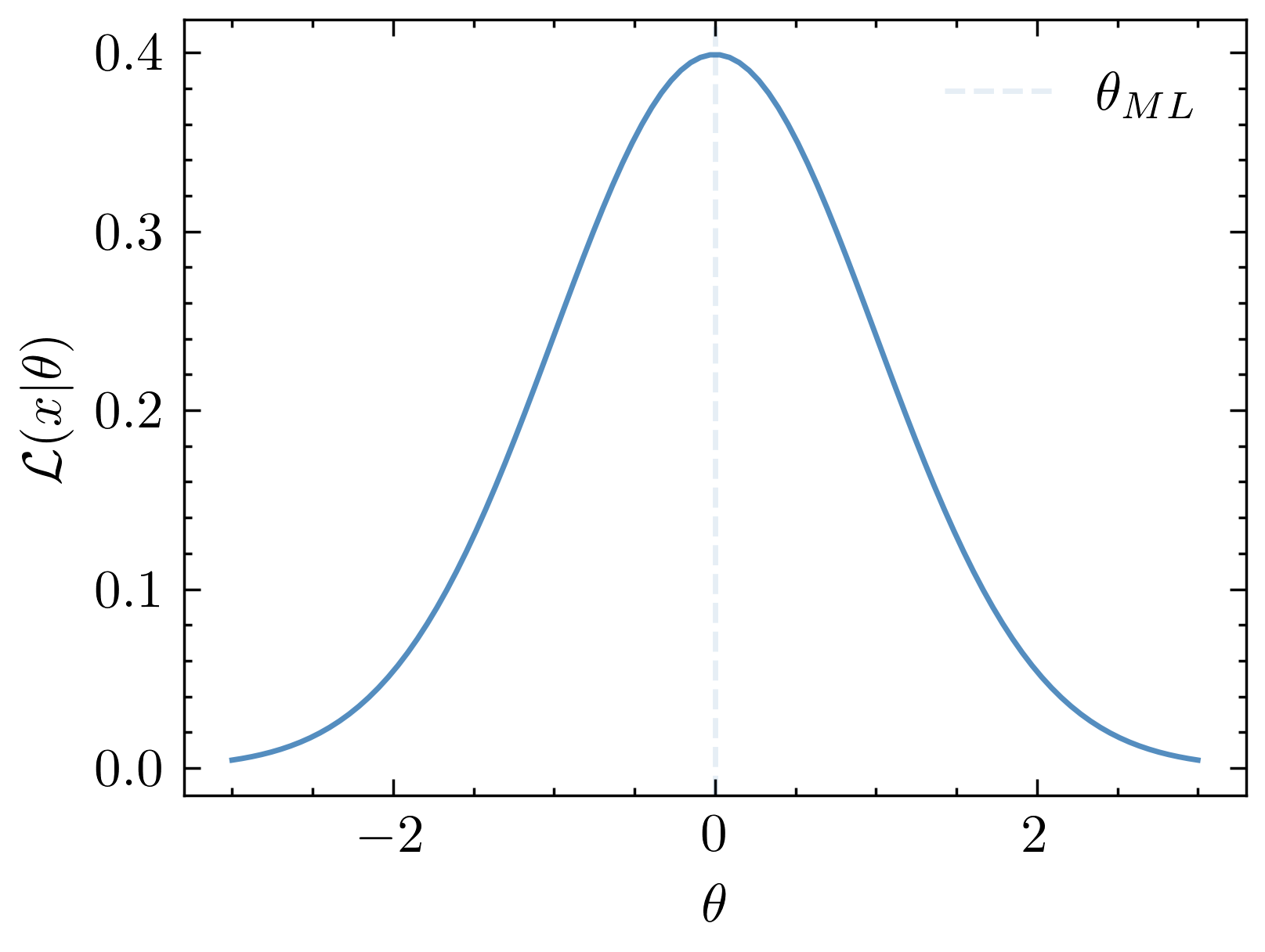
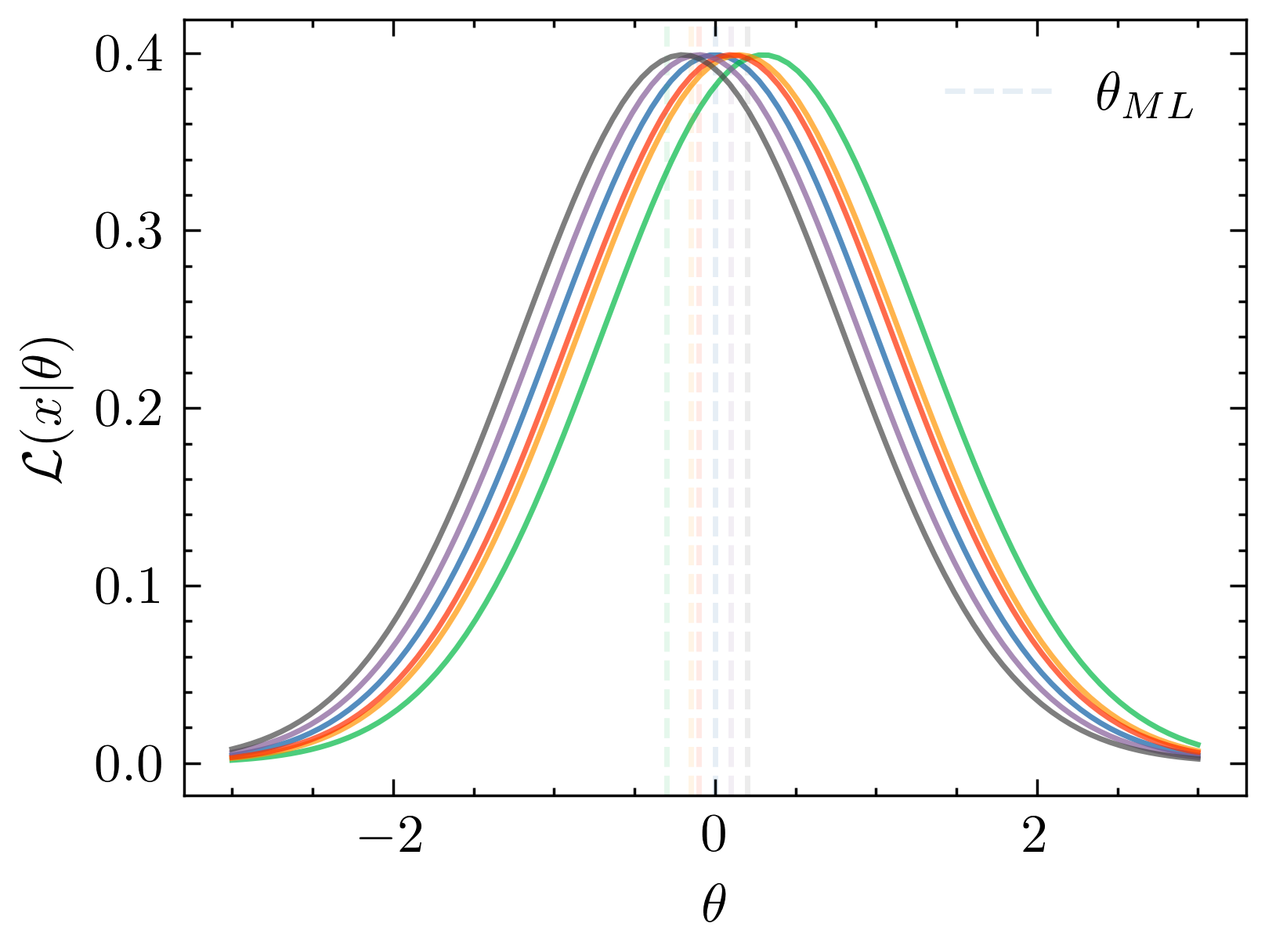
Estimating sensitivity to cosmology: Fisher information
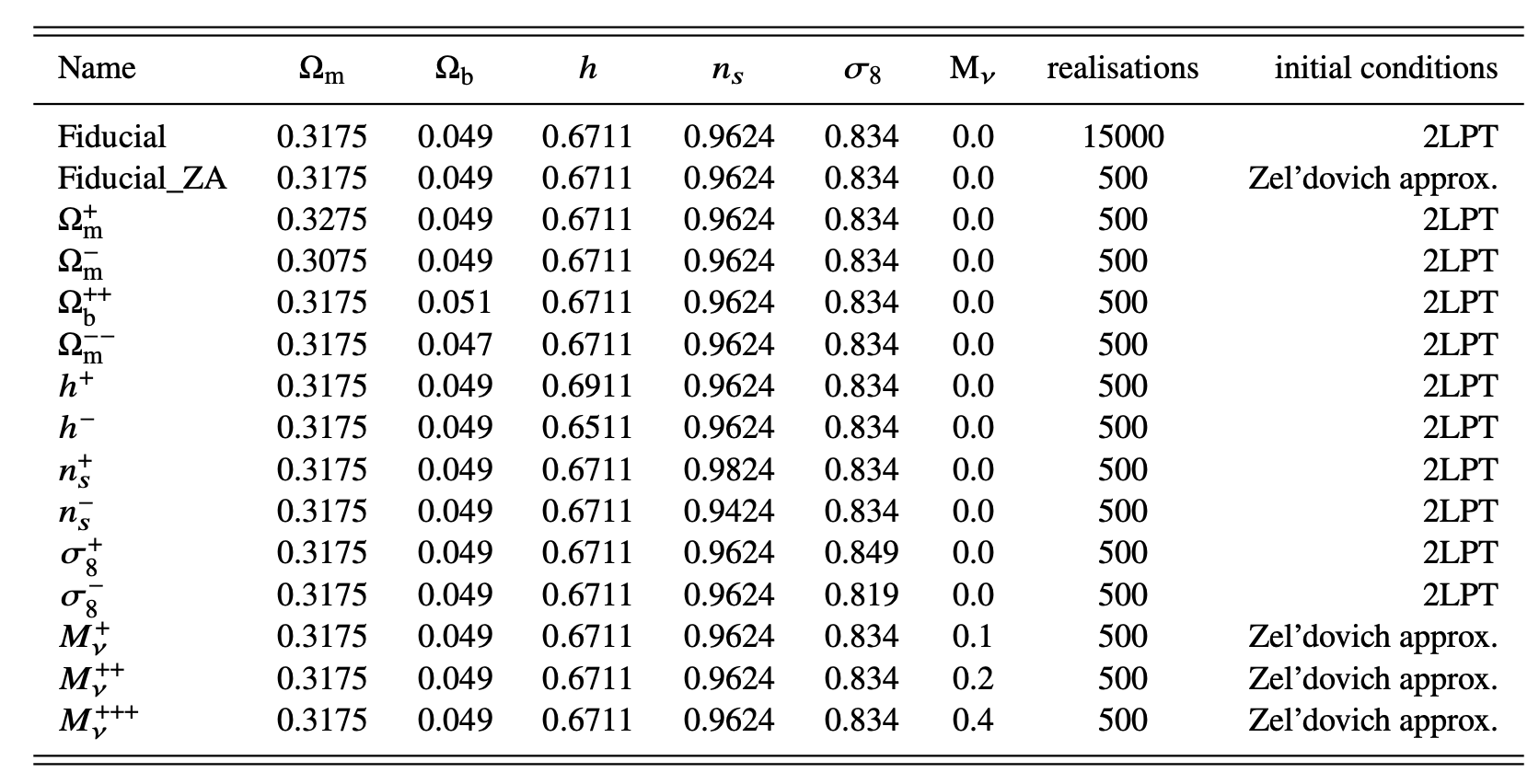
The Quijote simulations
arXiv:1909.05273
Covariance
Derivatives
\frac{\partial \bm{S}}{\partial \bm{\theta}} \simeq \frac{{\bm S}(\bm{\theta} + {\rm d}\bm{\theta}) - {\bm S}(\bm{\theta} - {\rm d}\bm{\theta})}{2 \rm{d}\bm{\theta}}
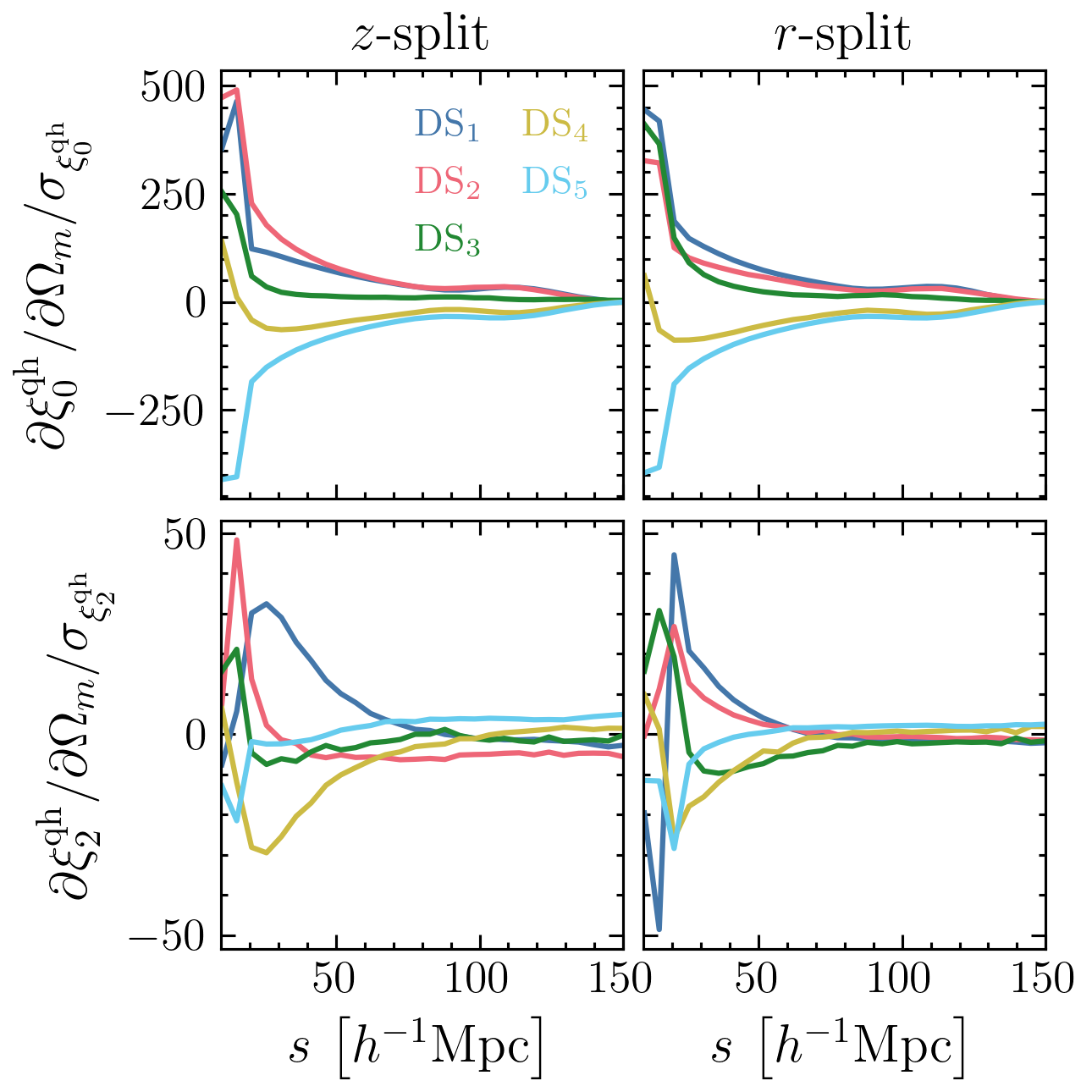
Finite differences
F_{\alpha \beta} = \frac{\partial S}{\partial \theta_\alpha} C^{-1} \frac{\partial S}{\partial \theta_\beta}
0
C = \frac{1}{n_{\rm sim} - 1} \sum_{k=1}^{n_{\rm sim}} \left({\bm{S}_{k}} - \overline{\bm{S}}\right)\left({\bm{S}_{k}} - \overline{\bm{S}}\right)
F_{\alpha \beta} = \frac{\partial S}{\partial \theta_\alpha} C^{-1} \frac{\partial S}{\partial \theta_\beta}
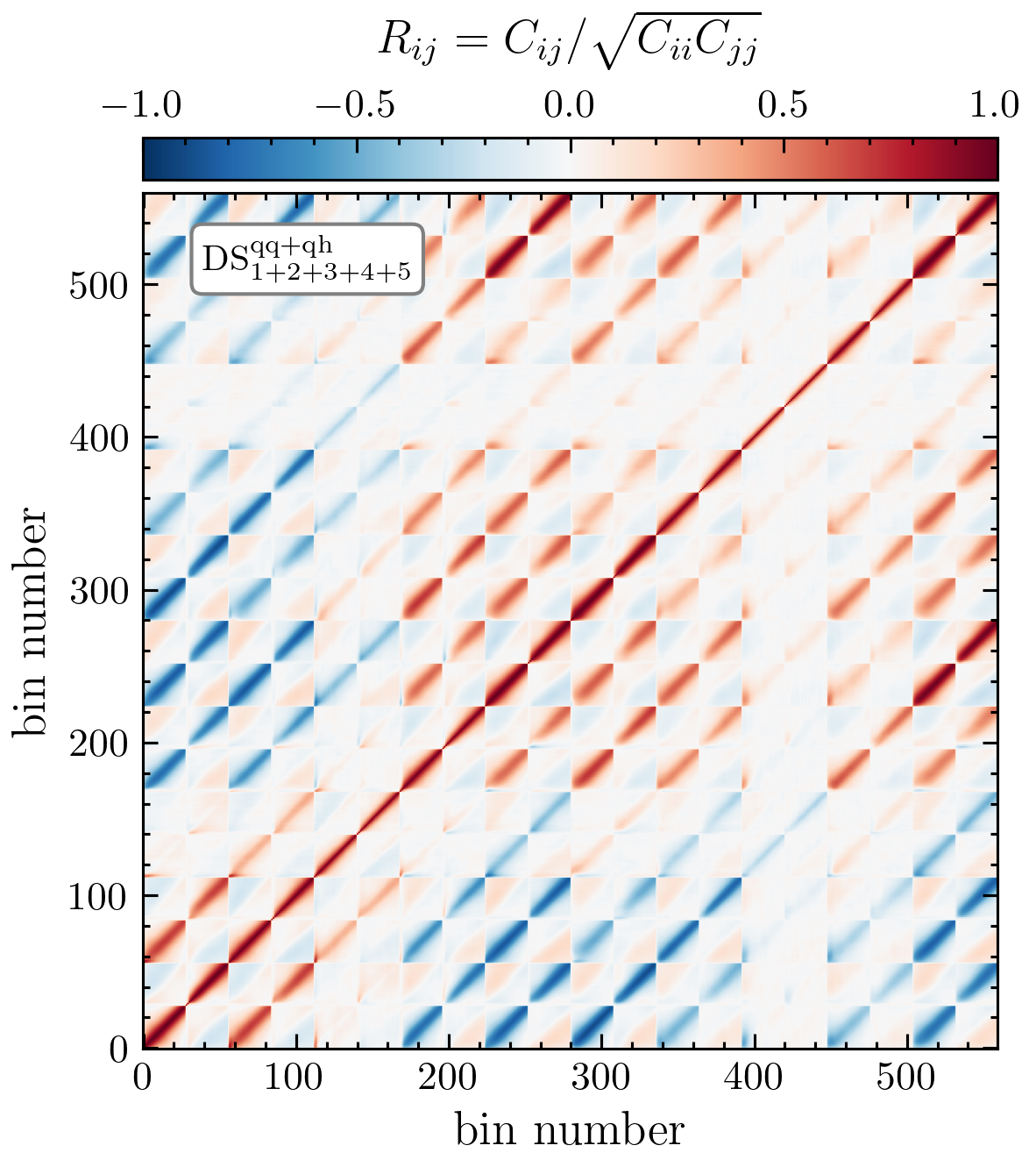
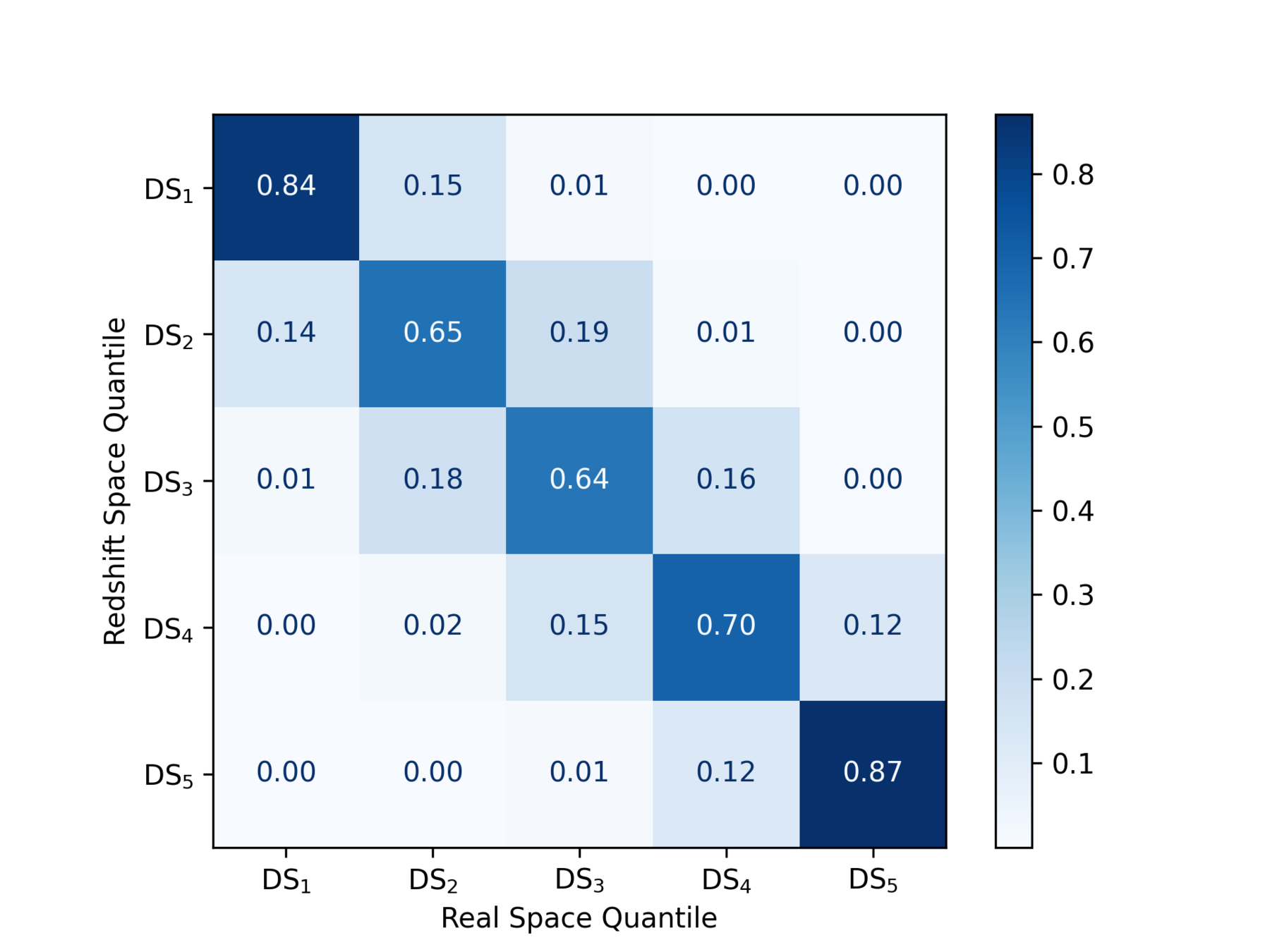
But, can we estimate densities realistically?
?
Real
Redshift
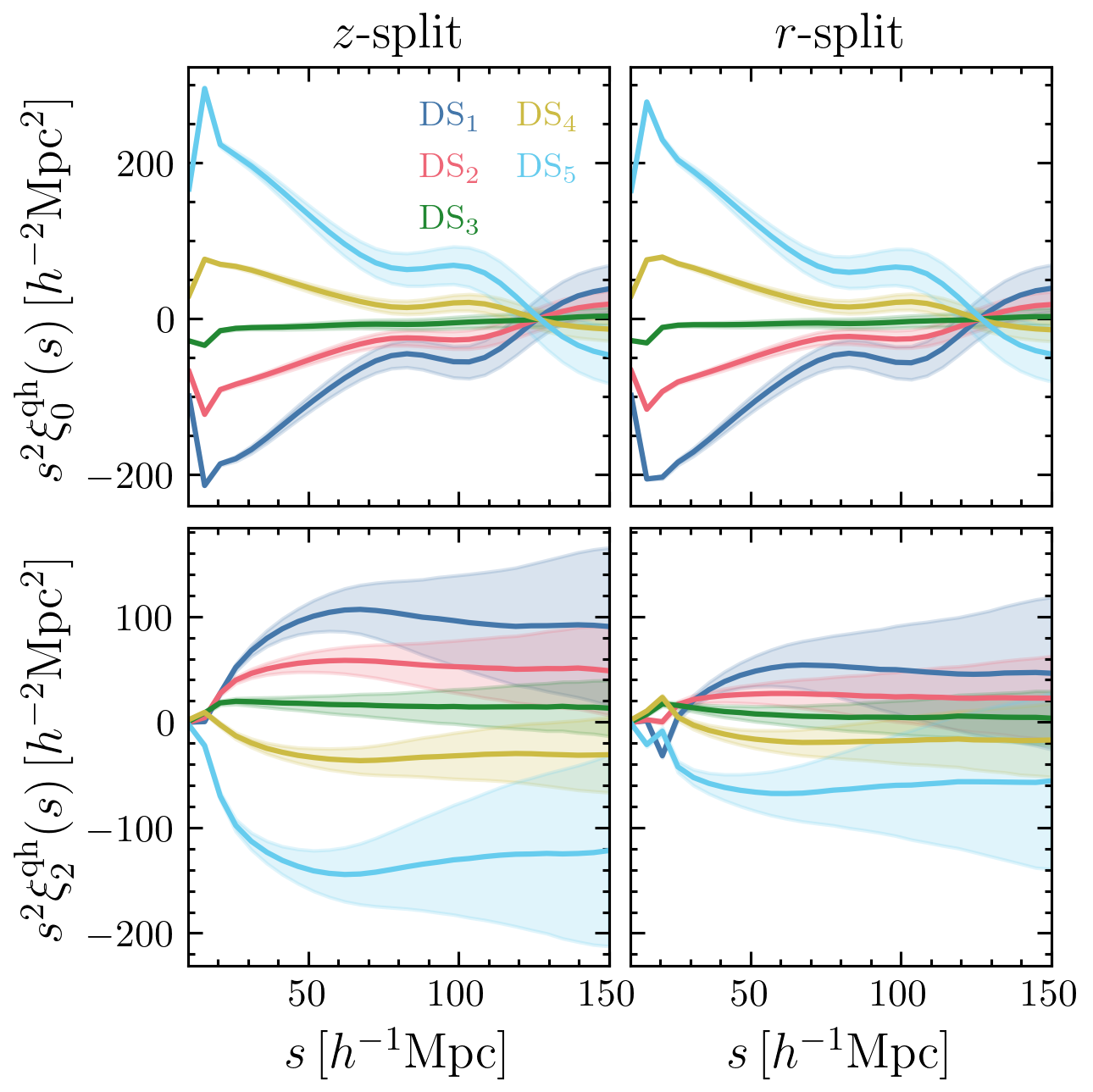
Cross-correlation between quintiles and haloes
Monopole
Quadrupole
s^2
s^2
Monopole
Quadrupole
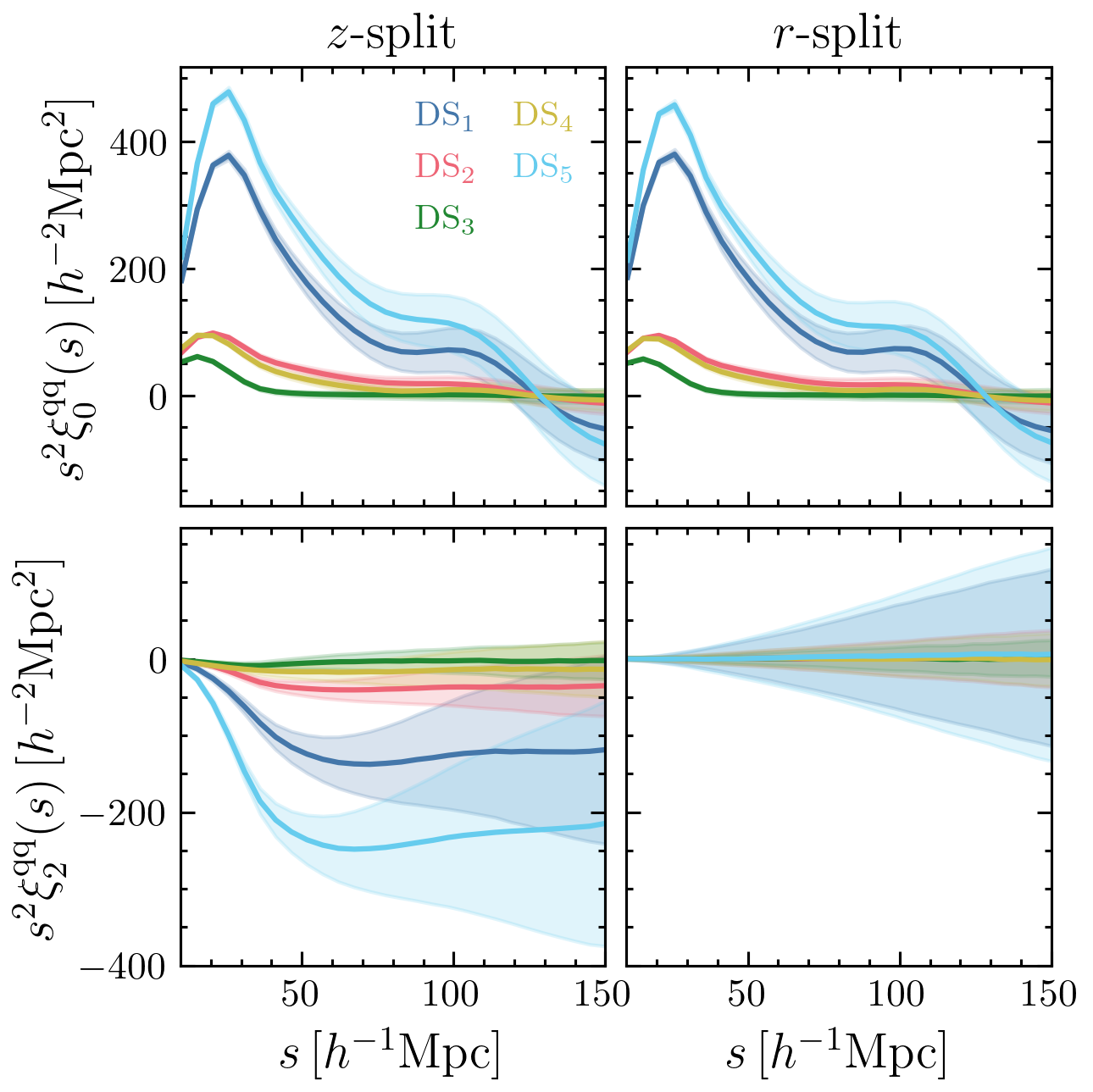
Autocorrelation of quintiles
s^2
s^2
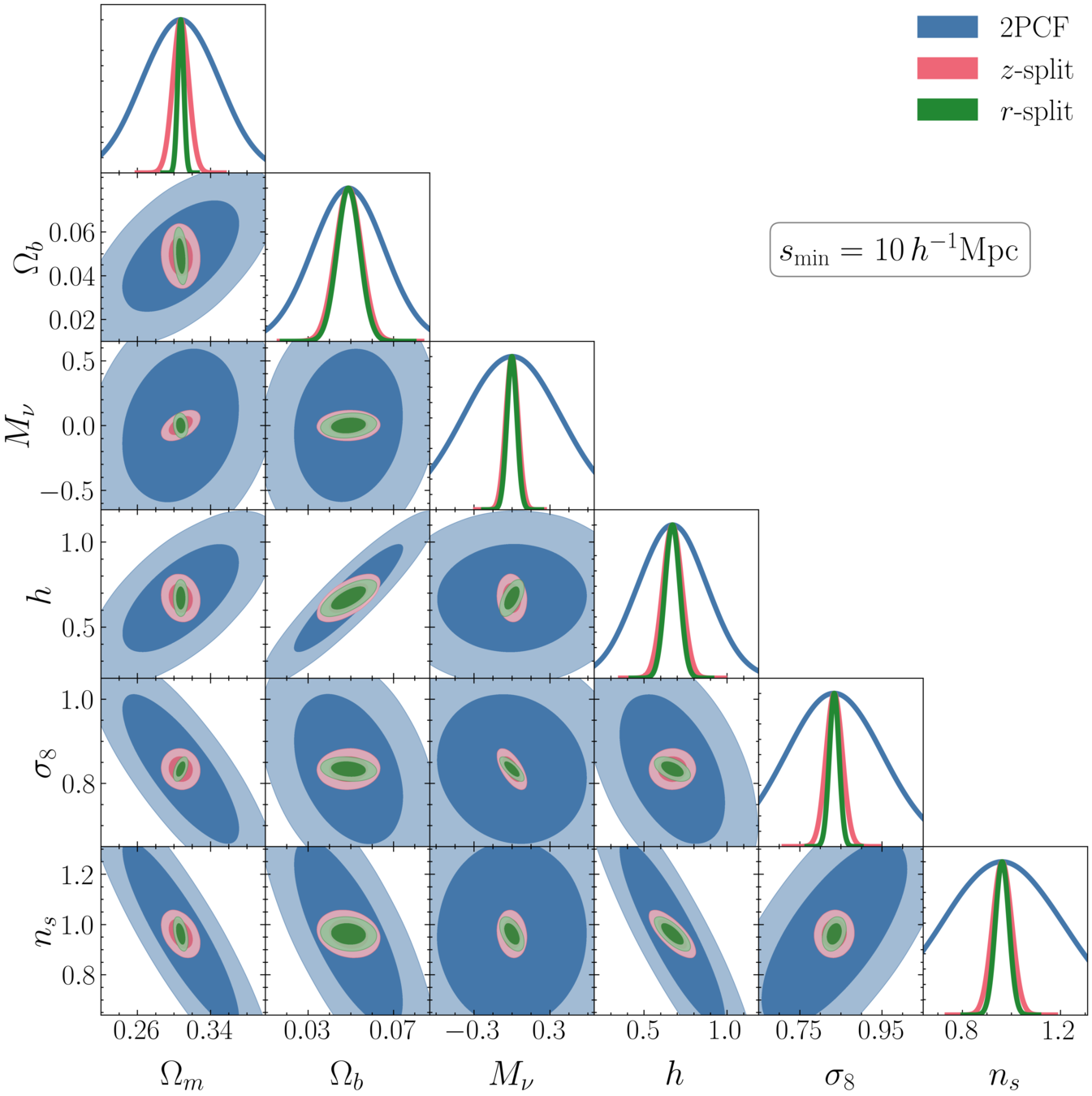
+ Galaxy-Halo connection
+ Cut-sky
+ Lightcone
+ Alcock-Paczinsky
+ Fiber collisions
Forward Model
N-body simulations
Observations
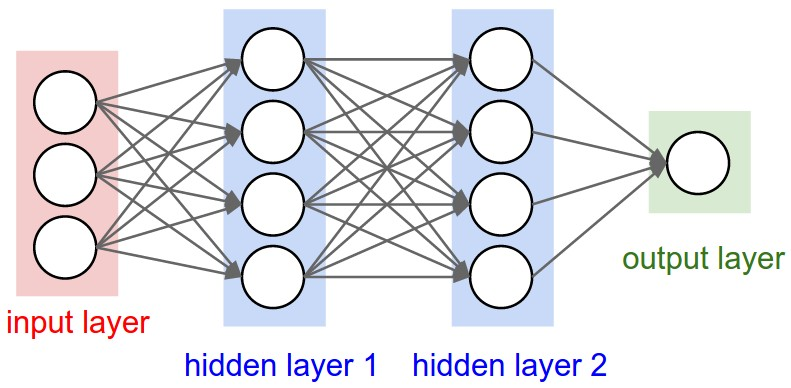
Credit: https://cs231n.github.io/convolutional-networks/
S(r)
\Omega_m
\Omega_\Lambda
...
\log(\mathcal{L}) \propto (S - S_\mathrm{obs}) C^{-1}(S - S_\mathrm{obs})
Neural Network emulator
\mathcal{O}(100) \,\,\, \mathrm{Nbody \, simulations}
Patchy to estimate covariances
Abacus HOD vs Uchuu SHAM
Density split in a BOSS CMASS
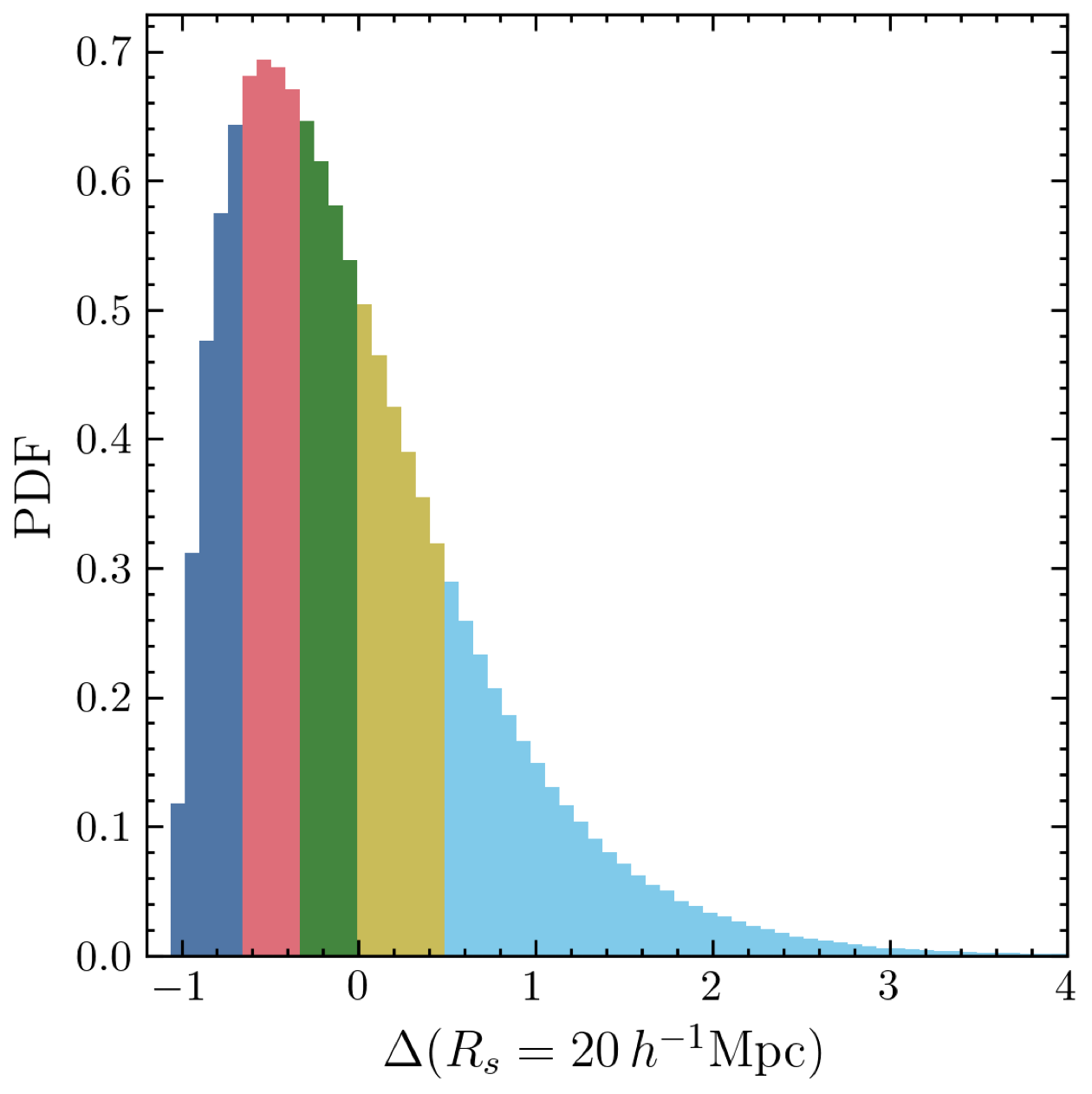
CMASS 0.46 < z < 0.6
Copy of Copy of Copy of DensitySplit
By carol cuesta
