Carol Cuesta-Lazaro (IAIFI Fellow)
in collaboration with Siddarth Mishra-Sharma
Generative models for the Large Scale Structure
Why Carol loves generative models and thinks you should love them too
Initial Conditions of the Universe
Laws of gravity
3-D distribution of galaxies
Which are the ICs of OUR Universe?
Primordial non-Gaussianity?
Probe Inflation
Galaxy formation
3-D distribution of dark matter
Is GR modified on large scales?
How do galaxies form?
Neutrino mass hierarchy?
ML for Large Scale Structure:
A wish list
Generative models
Learn p(x)
Evaluate the likelihood of a 3D map, as a function of the parameters of interest
1
Combine different galaxy properties (such as velocities and positions)
2
Sample 3D maps from the posterior distribution
3
p(
)
|
\mathrm{Cosmology}
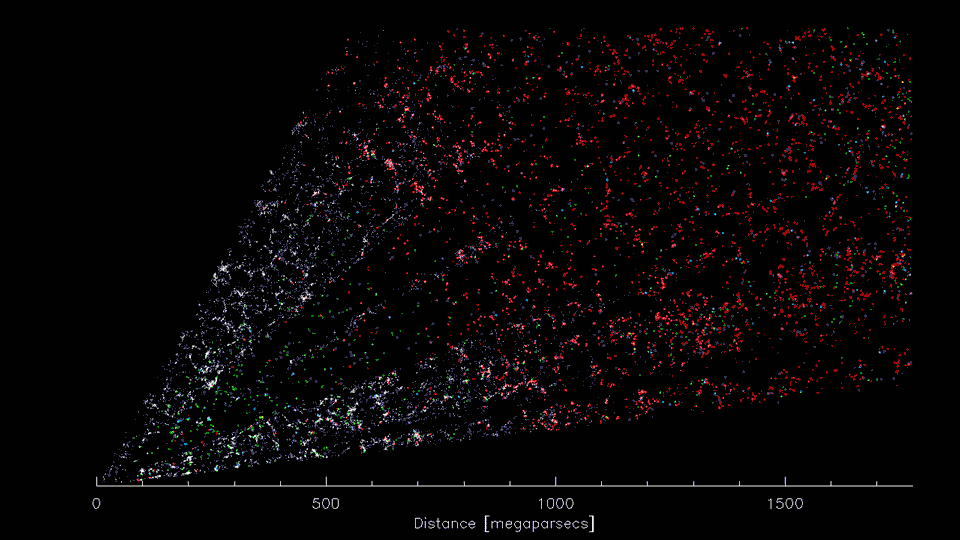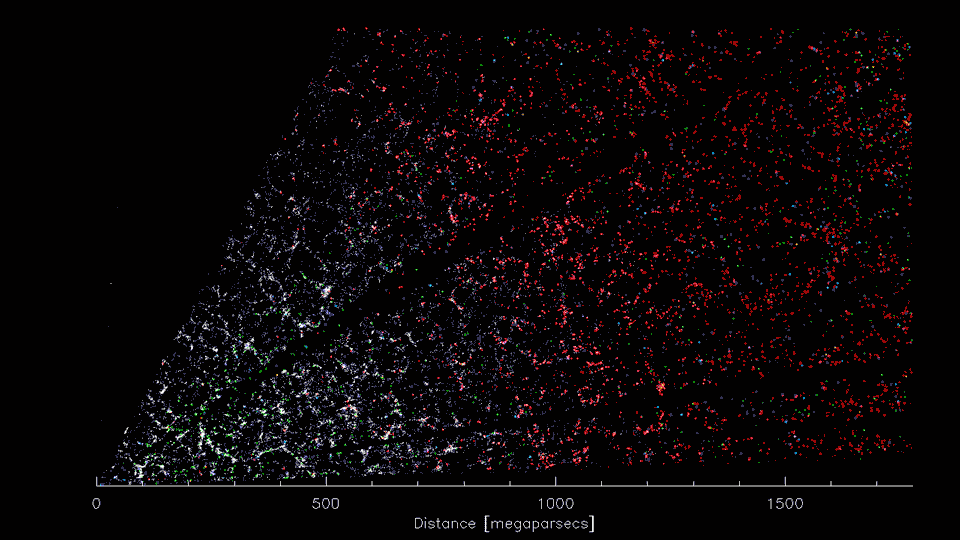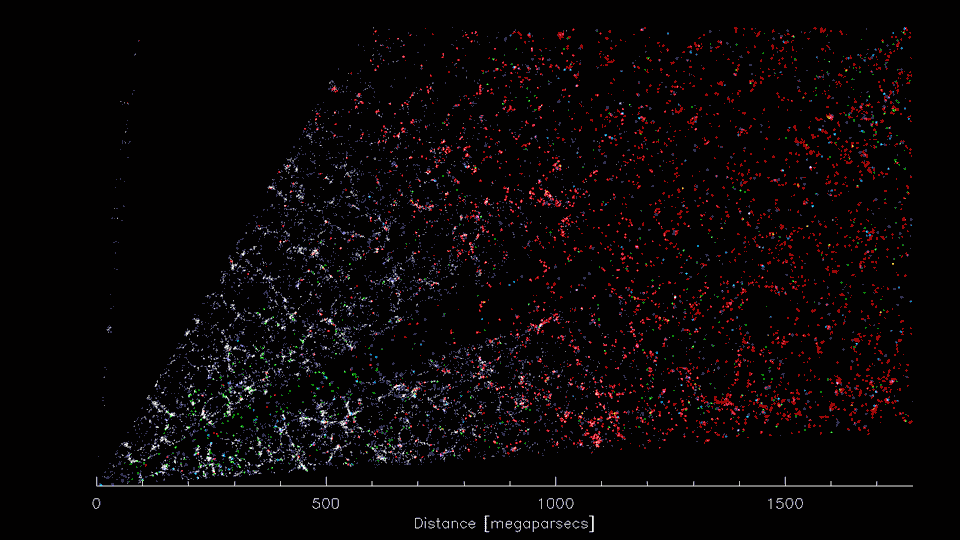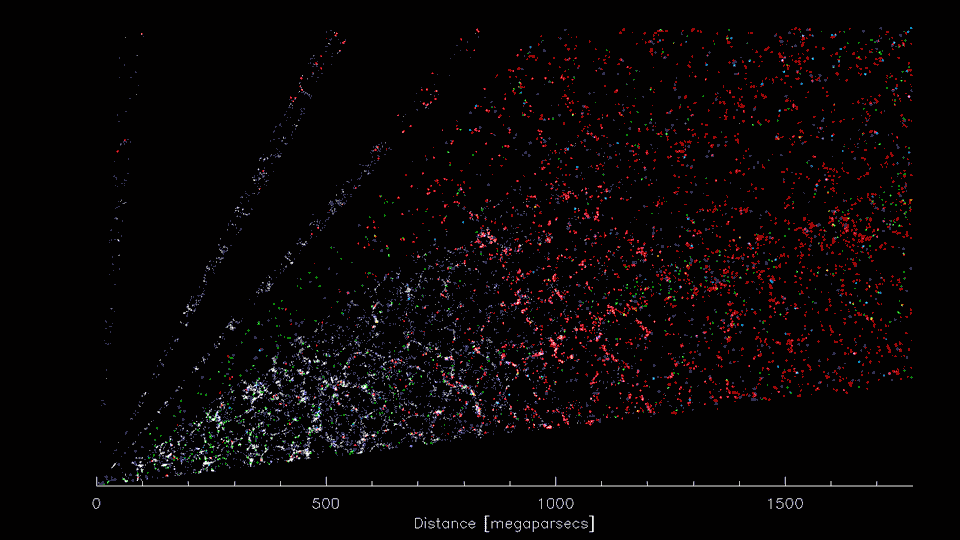
"What I cannot create, I do not understand"
p(y|x)
p(x|y) = \frac{p(y|x)p(x)}{p(y)}
p(x|y)
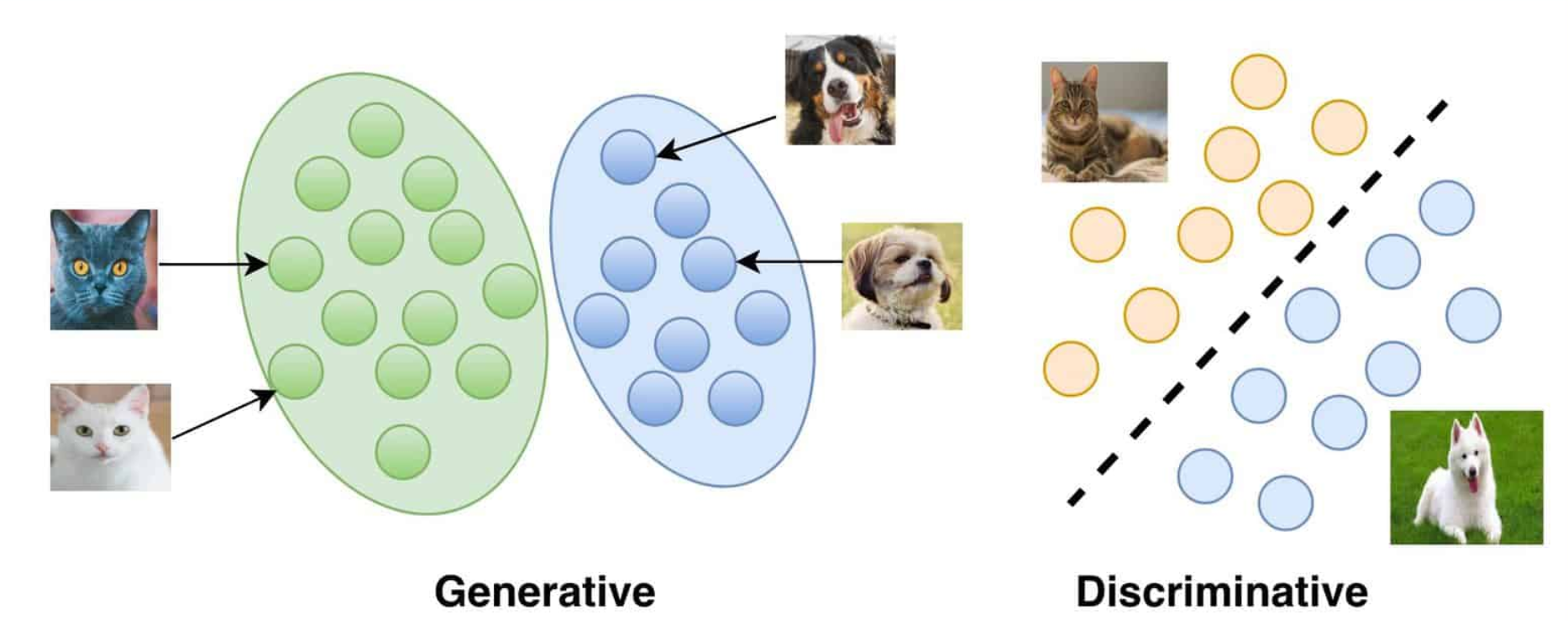
https://vitalflux.com/generative-vs-discriminative-models-examples/
Hall of fame
A teddy bear wearing a motorcycle helmet and cape is standing in front of Loch Awe with Kilchurn Castle behind him driving a speed boat near the Golden Gate Bridge
https://parti.research.google
Emulators of complex processes
Anomaly detection
arXiv:2010.11202
Estimating non-gaussian likelihoods
Model posterior distributions (uncertainties)
\mathcal{L}(y|\theta)
arXiv:2304.03788
Explicit Density
Implicit Density
Tractable Density
Approximate Density
Normalising flows
Variational Autoencoders
Diffusion models
Generative Adversarial Networks
The zoo of generative models
z_T
z_{0}
z_{1}
z_{2}
p(z_{t-1}|z_t)
p(z_t|z_{t-1})
Reverse diffusion: Denoise previous step
Forward diffusion: Add Gaussian noise (fixed)
Diffusion models
A person half Yoda half Gandalf
z_T
z_{0}
z_{1}
Diffusion on 3D coordinates
z_{2}
q_\theta(z_{t-1}|z_t)
p(z_t|z_{t-1})
Reverse diffusion: Denoise previous step
Forward diffusion: Add Gaussian noise (fixed)
Cosmology
p(x,y,z|\Omega_m, \sigma_8)
p(x,y,z, v_x, v_y, v_z, M_h|\Omega_m, \sigma_8)
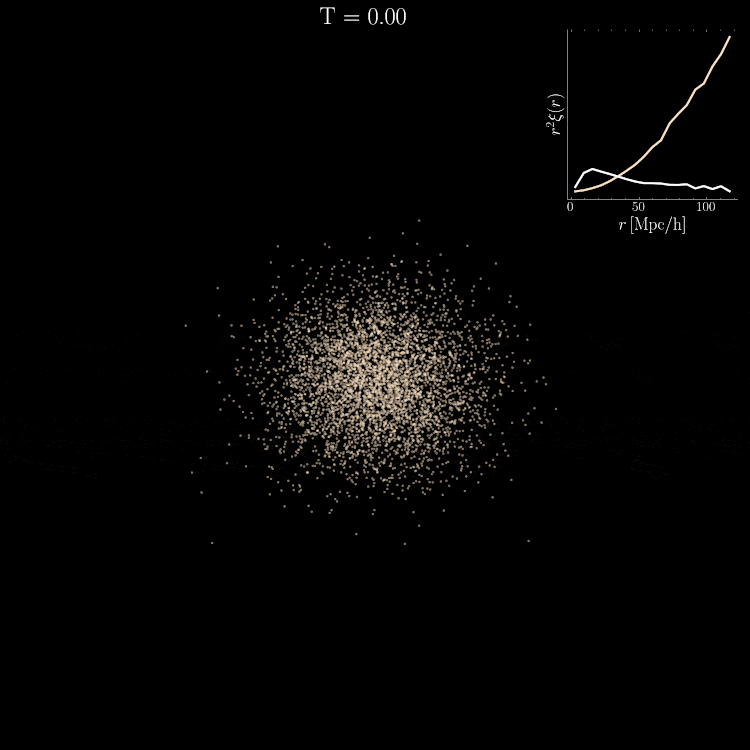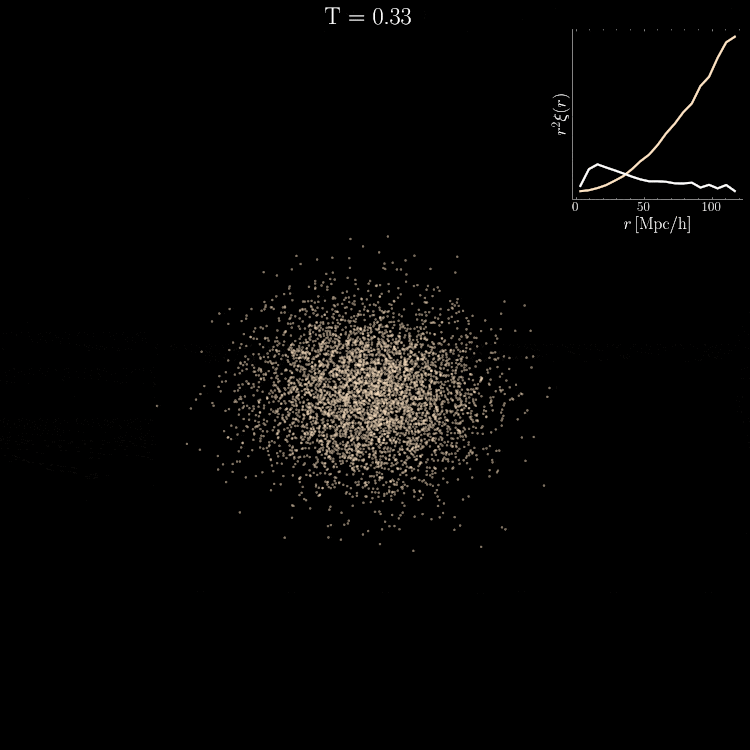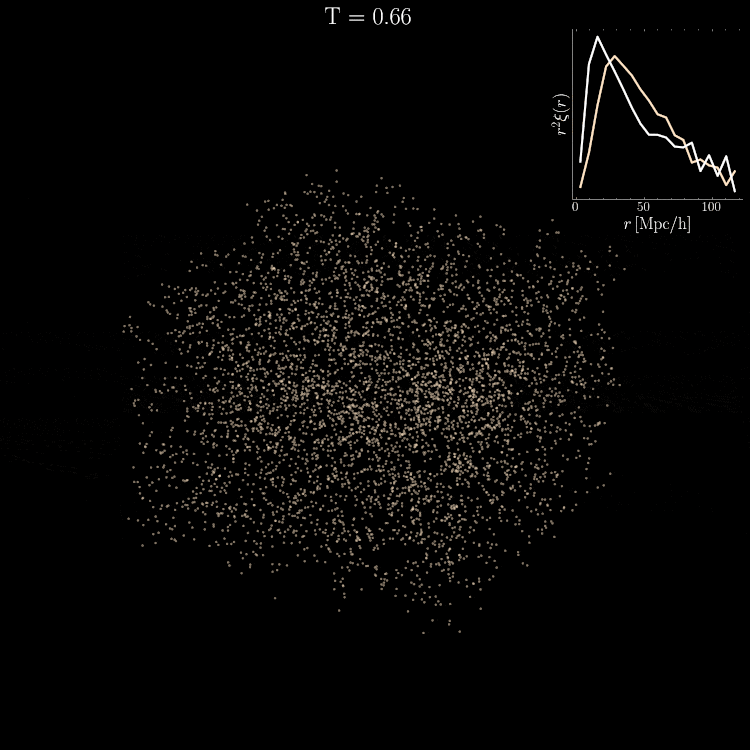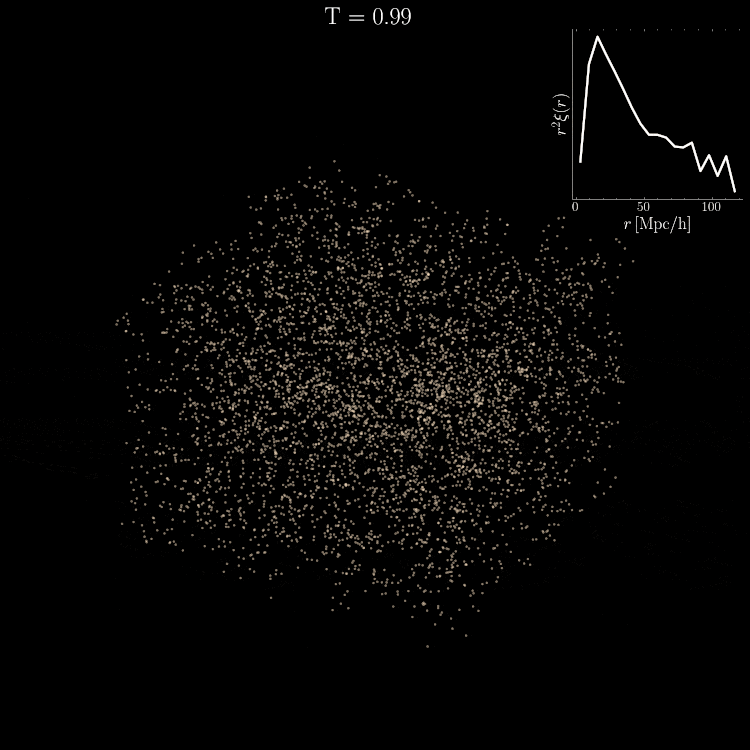
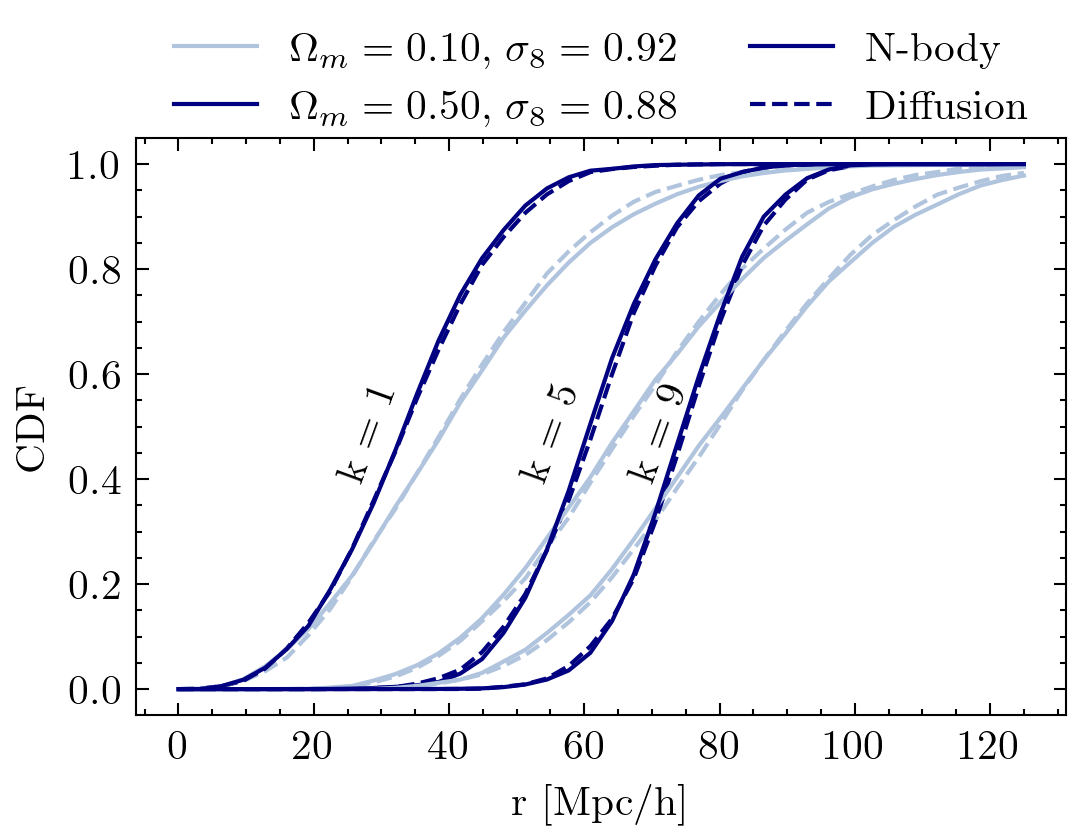
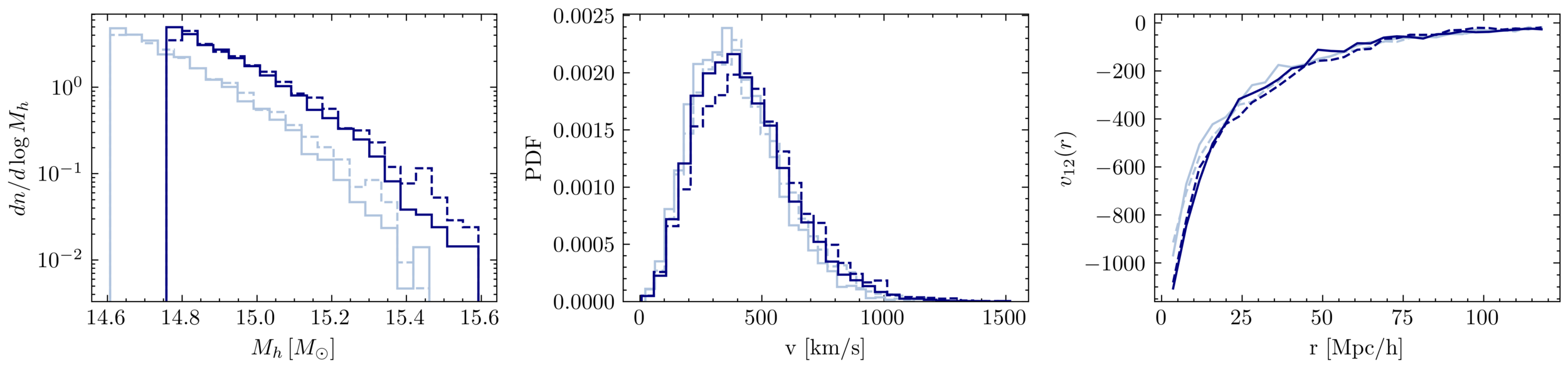
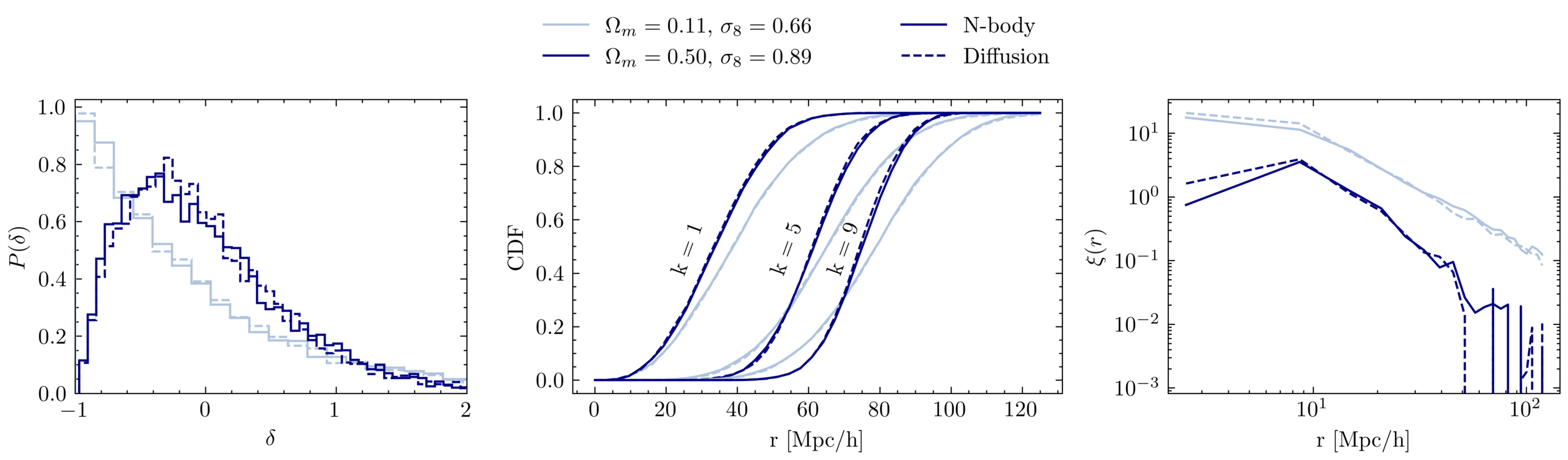
Density PDF
kNN
TPCF
Halo Mass Function
Velocity
Mean pairwise velocity
z_T
z_{0}
z_{1}
Evidence Lower Bound (ELBO)
z_{2}
q_\theta(z_{t-1}|z_t) \approx p(z_{t-1}|z_{t})
p(z_t|z_{t-1})
p(z_{t-1}|z_{t})
Variational Inference
Approximate the true posterior of the latent variables by a parametric distribution
\log p(\boldsymbol{x}) =
\geq \mathbb{E}_{q_{\boldsymbol{\phi}}(\boldsymbol{z}\mid\boldsymbol{x})}\left[\log\frac{p(\boldsymbol{x}, \boldsymbol{z})}{q_{\boldsymbol{\phi}}(\boldsymbol{z}\mid\boldsymbol{x})}\right]
\mathbb{E}_{q_{\boldsymbol{\phi}}(\boldsymbol{z}\mid\boldsymbol{x})}\left[\log\frac{p(\boldsymbol{x}, \boldsymbol{z})}{q_{\boldsymbol{\phi}}(\boldsymbol{z}\mid\boldsymbol{x})}\right] + \mathcal{D}_{\text{KL}}(q_{\boldsymbol{\phi}}(\boldsymbol{z}\mid\boldsymbol{x}) \mid\mid p(\boldsymbol{z}\mid\boldsymbol{x}))
Evidence Lower Bound
Distance to true posterior
q_\theta(z|x) \approx p(z|x)
Find
1. ELBO is a lower bound of the evidence
2. Maximising ELBO = Minimising KL
Maximise ELBO to maximise ev/likelihood
Maximise ELBO to approximate true posterior
Setting tight constraints with only 5000 halo positions
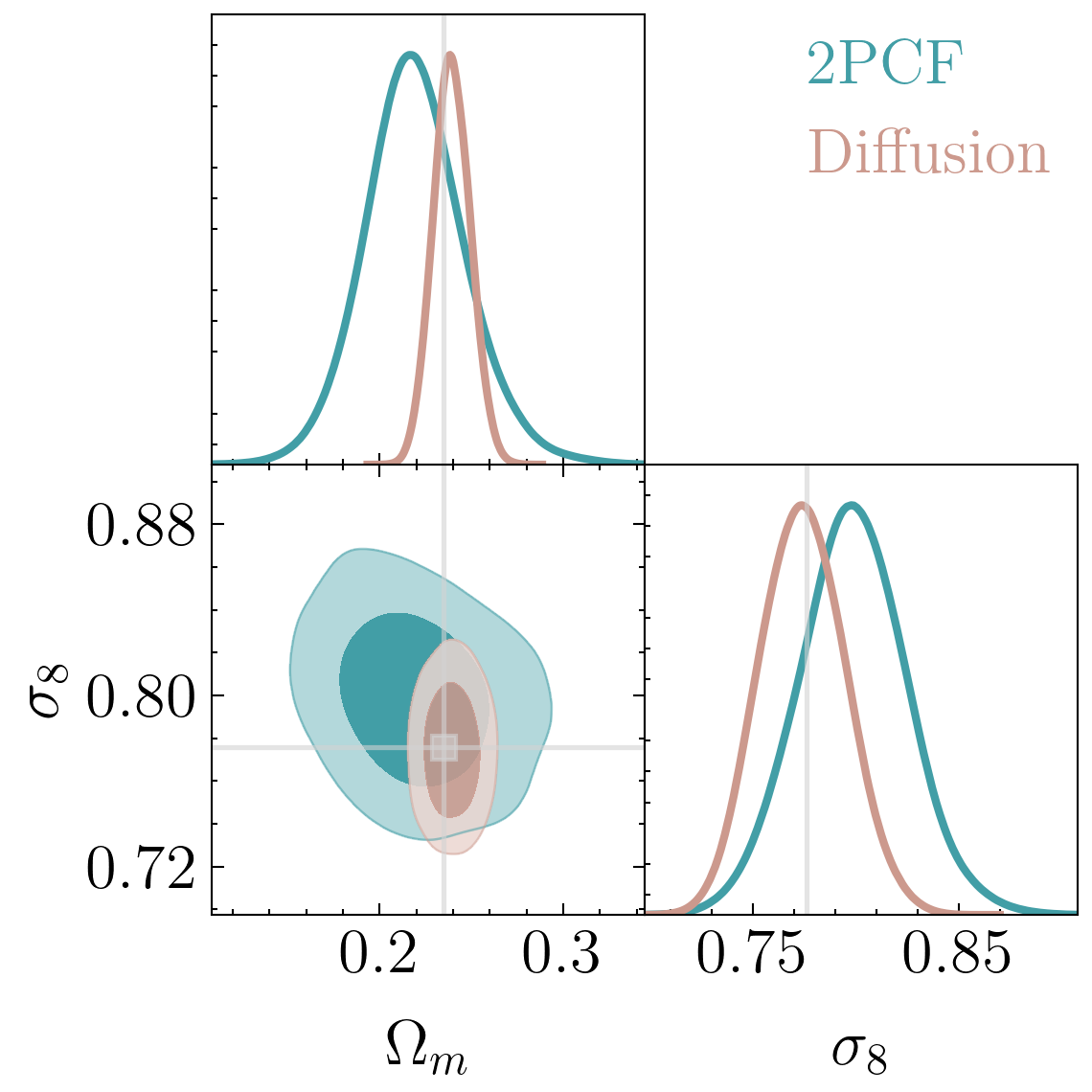
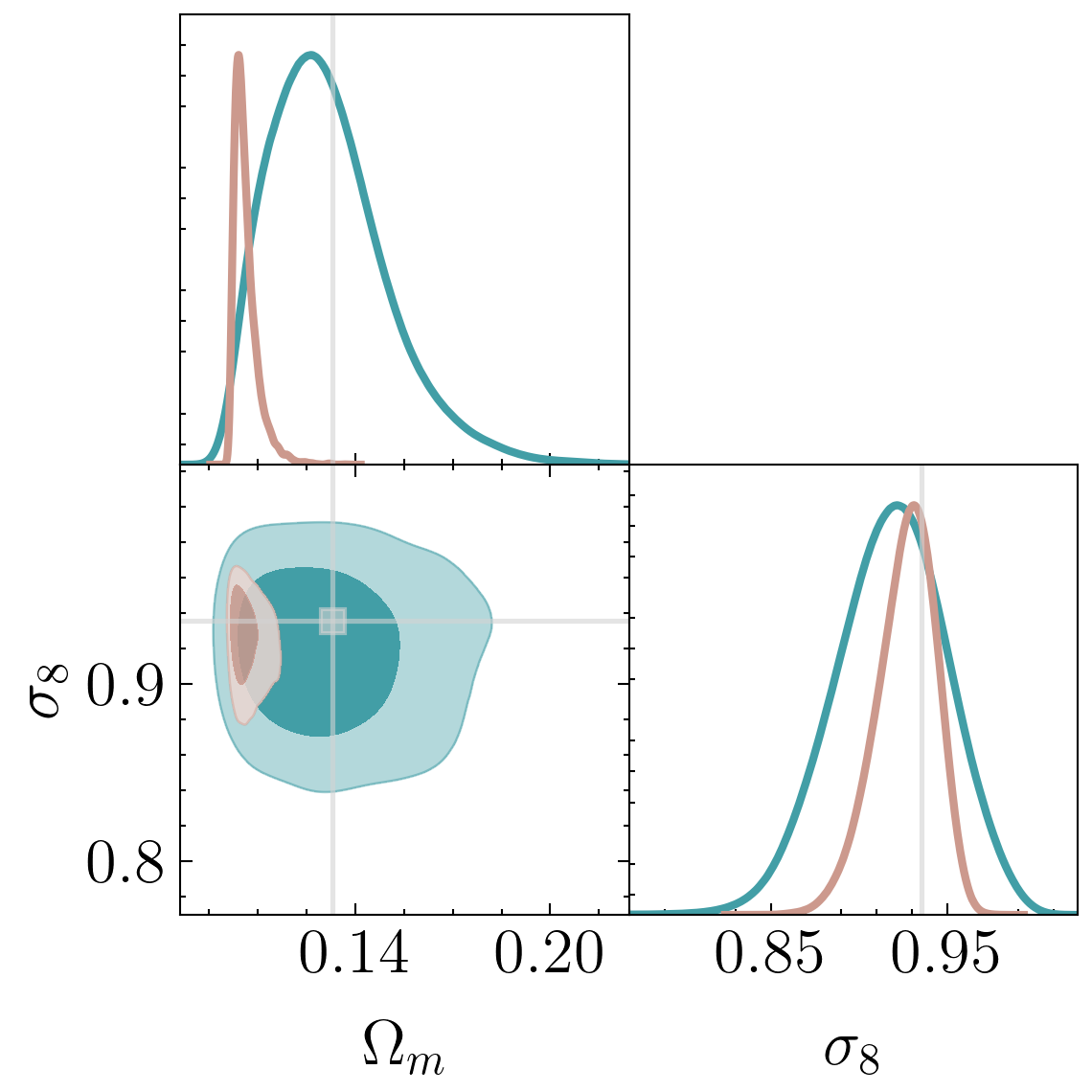
+ Galaxy formation
+ Observational systematics (Cut-sky, Fiber collisions)
+ Lightcone, Redshift Space Distortions....
Forward Model
N-body simulations
Observations
SIMBIG arXiv:2211.00723
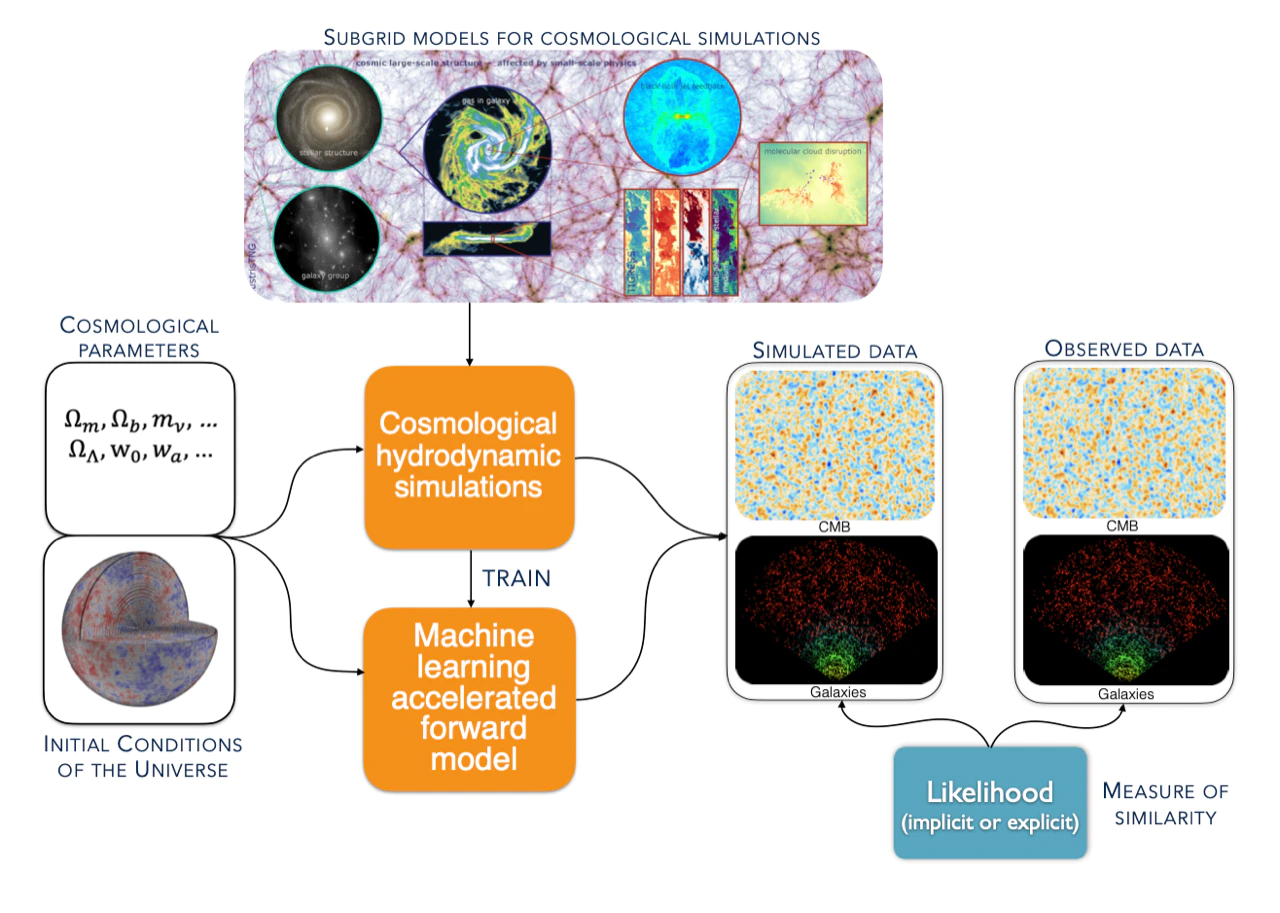
We can simulate the observable Universe, we just need hydrodynamical simulations
25 \, h^{-1}\mathrm{Mpc}
What are subresolution models?
10^{10} - 10^{11} M_\odot
Super massive black hole seeding in dark matter halos
BH feedback impacts galactic scales
Black holes can also grow through mergers
Effective models of astrophysical processes needed due to limited numerical resolutions or limited physical models
they can even teleport!
F_\theta(\mathbf{x},a) = \frac{3 \Omega_m}{2} \nabla \left[ \phi_\mathrm{PM}(\mathbf{x}) \right]
Particle Mesh to N-body
F_\theta(\mathbf{x},a) = \frac{3 \Omega_m}{2} \nabla \left[ \phi_\mathrm{PM}(\mathbf{x}) + \phi_\theta (\mathbf{x},\delta,\phi_\mathrm{PM},a) \right]
arXiv:2207.05509
Low Res Potential
True Potential
\delta
Corrected Potential
True Potential
\delta
We can't model galaxy formation, how do we make our models robust?
(\theta_\mathrm{sims}, x_\mathrm{sims}: \small{\mathrm{linear}})
x_\mathrm{obs}: \small{\mathrm{nonlinear}}
Increase the evidence of the observations
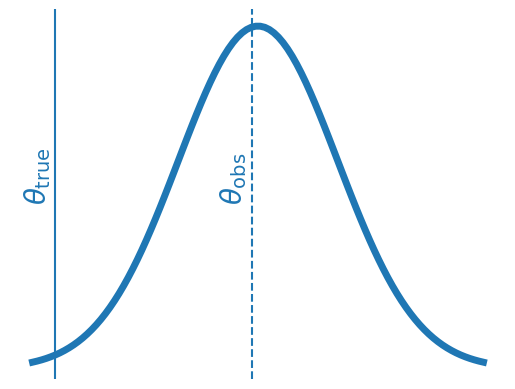
Robust Summarisation
\theta_\mathrm{obs} \mathrm{?}
\mathcal{L} = p(\theta_\mathrm{sims}|S(x_\mathrm{sims})) + \lambda p_\mathrm{sims}(S(x_\mathrm{obs}))
\mathcal{L} = p(\theta_\mathrm{sims}|S(x_\mathrm{sims}))
What ML can do for cosmology
- ML to accelerate non-linear predictions and density estimation
- Can ML extract **all** the information that there is at the field-level in the non-linear regime?
- Compare data and simulations, point us to the missing pieces?
cuestalz@mit.edu
Graph Neural Networks in a nutshell
\mathcal{G} = h^{L}_i, e^{L}_{ij} \rightarrow h^{L+1}_i, e^{L+1}_{ij}
e^{L+1}_{ij} = \phi_e(e^L_{ij}, h^L_i, h^L_j)
h^{L+1}_{i} = \phi_h( h^L_i, \mathcal{A}_j e^{L+1}_{ij})
edge embedding
node embedding
e_{ij}
h_i = \{\mathrm{positions}, \mathrm{velocities}...\}
h_j
Invariance vs Equivariance
r
\theta
\phi
Invariance
Scalar interactions
r
Equivariance
What can we do with vectors?
Tensor products
v_i
v_j
h_0
h_1
h_5
h_4
h_2
h_3
h_6
e_{01}
e_{12}
Node features
Edge features
\mathcal{G} = h^{L}_i, e^{L}_{ij} \rightarrow h^{L+1}_i, e^{L+1}_{ij}
e^{L+1}_{ij} = \phi_e(e^L_{ij}, h^L_i, h^L_j)
edge embedding
h^{L+1}_{i} = \phi_h( h^L_i, \mathcal{A}_j e^{L+1}_{ij})
node embedding
Input
noisy halo properties
Output
noise prediction
Copy of Copy of deck
By carol cuesta
