Redshift surveys in a nutshell
Learning summary statistics with ML
Carolina Cuesta-Lazaro
Newcastle Astro Journal Club
Collaborators: Cheng-Zong Ruan, Yosuke Kobayashi, Enrique Paillas, Alexander Eggemeier, Pauline Zarrouk, Sownak Bose, Takahiro Nishimichi, Baojiu Li, Carlton Baugh
Medical Imaging
Epidemiology: Agent Based simulations
OBSERVED
SIMULATED
Cosmology
Simulations
HPC
Science question
Statistics ML
Fifth forces modify structure growth
GROWTH
- GRAVITY
- FIFTH FORCE
+ EXPANSION
Credit: Cartoon depicting Willem de Sitter as Lambda from Algemeen Handelsblad (1930).
Credit: https://arxiv.org/abs/1912.09383
S_8 = \sigma_8 \sqrt{\Omega_m / 0.3}
Resolving tensions
(\vec{\theta}_i, z_i)
z_i = z_{\mathrm{Cosmological} }
+ z_{\mathrm{Doppler}}
\chi(z) = \int_0^z \frac{dz'}{H(z')}
+ \frac{v_{\mathrm{pec}}}{aH(a)}
\chi_i
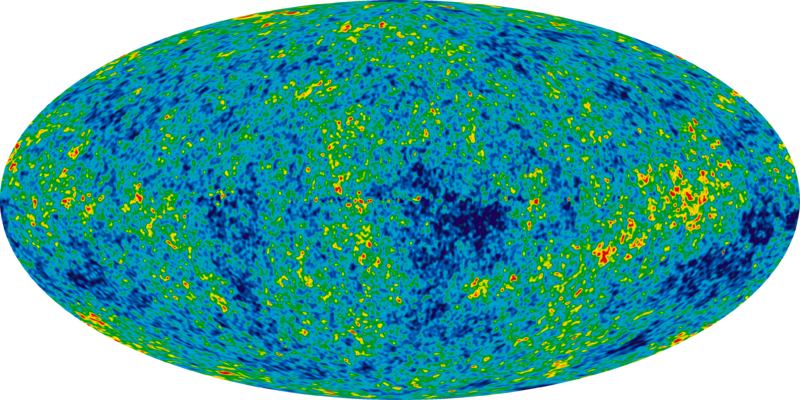
Early Universe
~linear
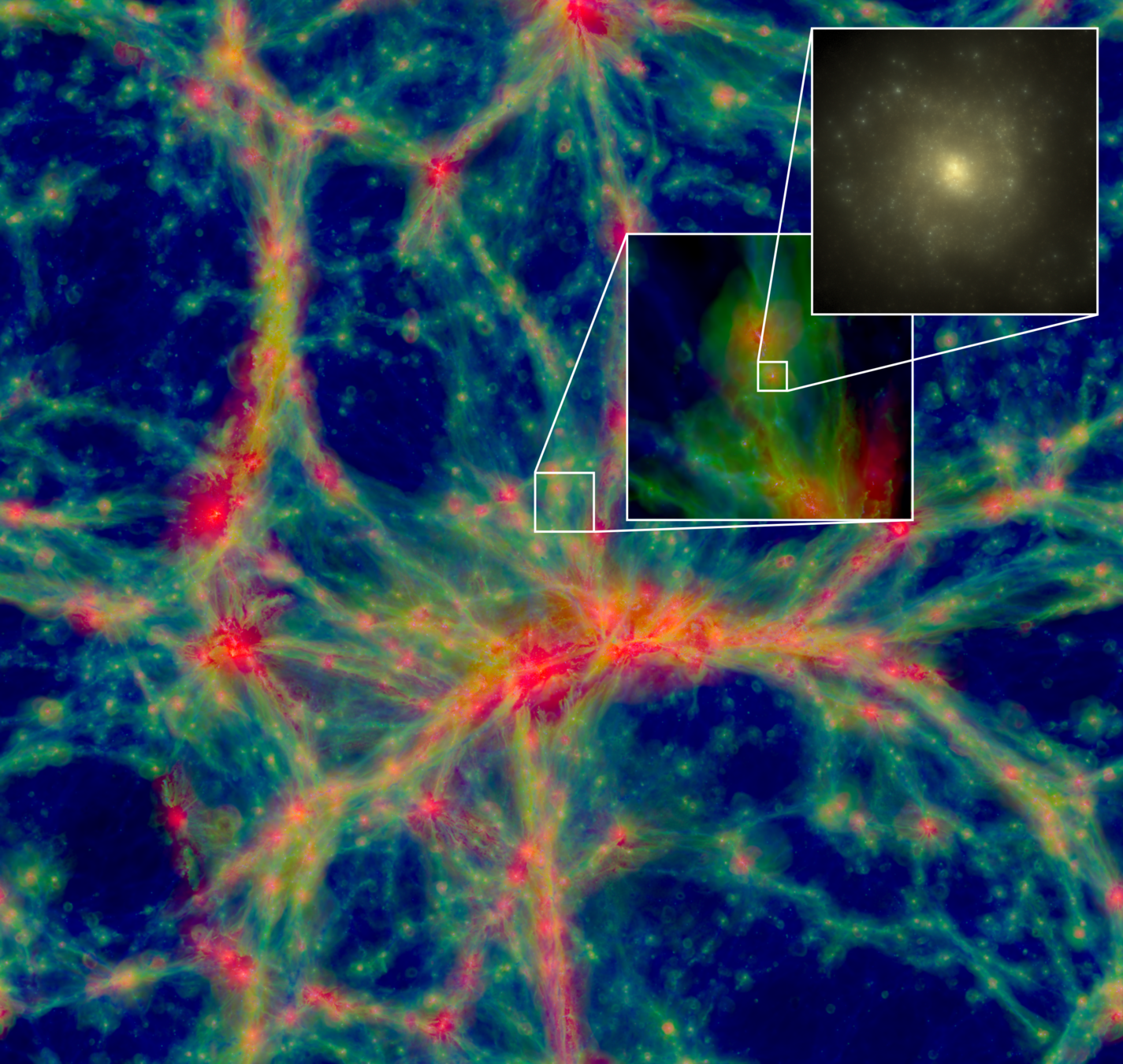
Gravity
Late Universe
Non-linear
Credit: S. Codis+16
\delta = \frac{\rho - \bar{\rho}}{\bar{\rho}} << 1
\delta >> 1
Non-linearity = PT predictions inaccurate
Credit: S. Codis+16
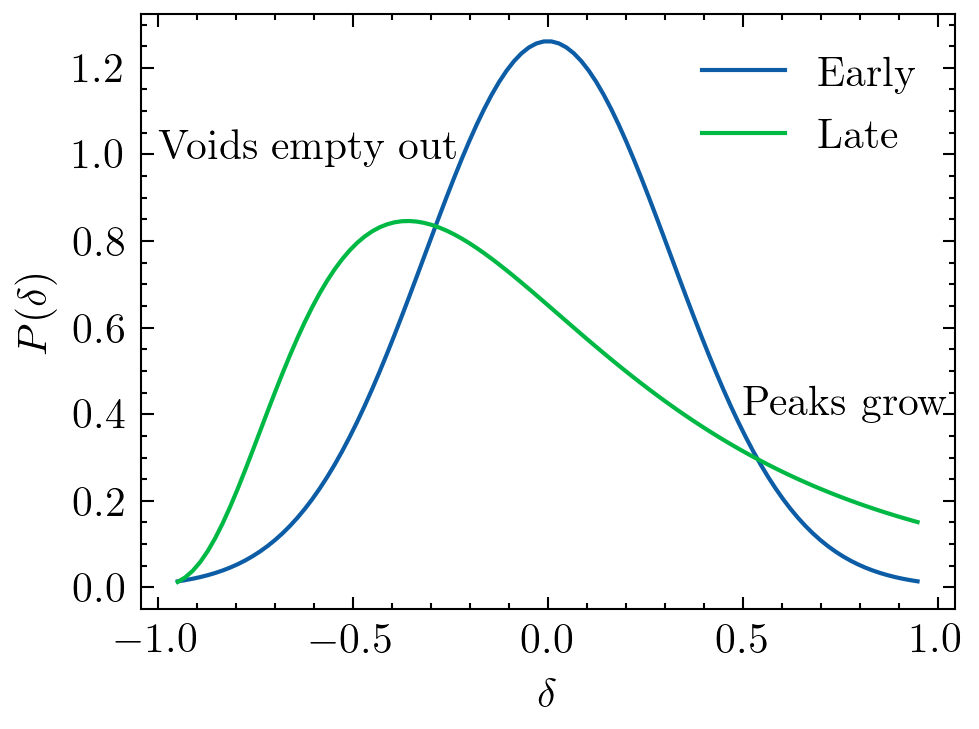
Early Universe
~linear
Gravity
Late Universe
Non-linear
Credit: S. Codis+16
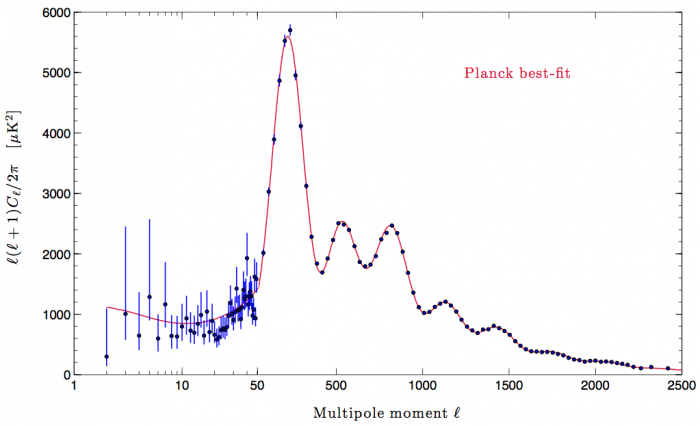
Non-Guassianity
Second moment not optimal
\delta = \frac{\rho - \bar{\rho}}{\bar{\rho}} << 1
\delta >> 1
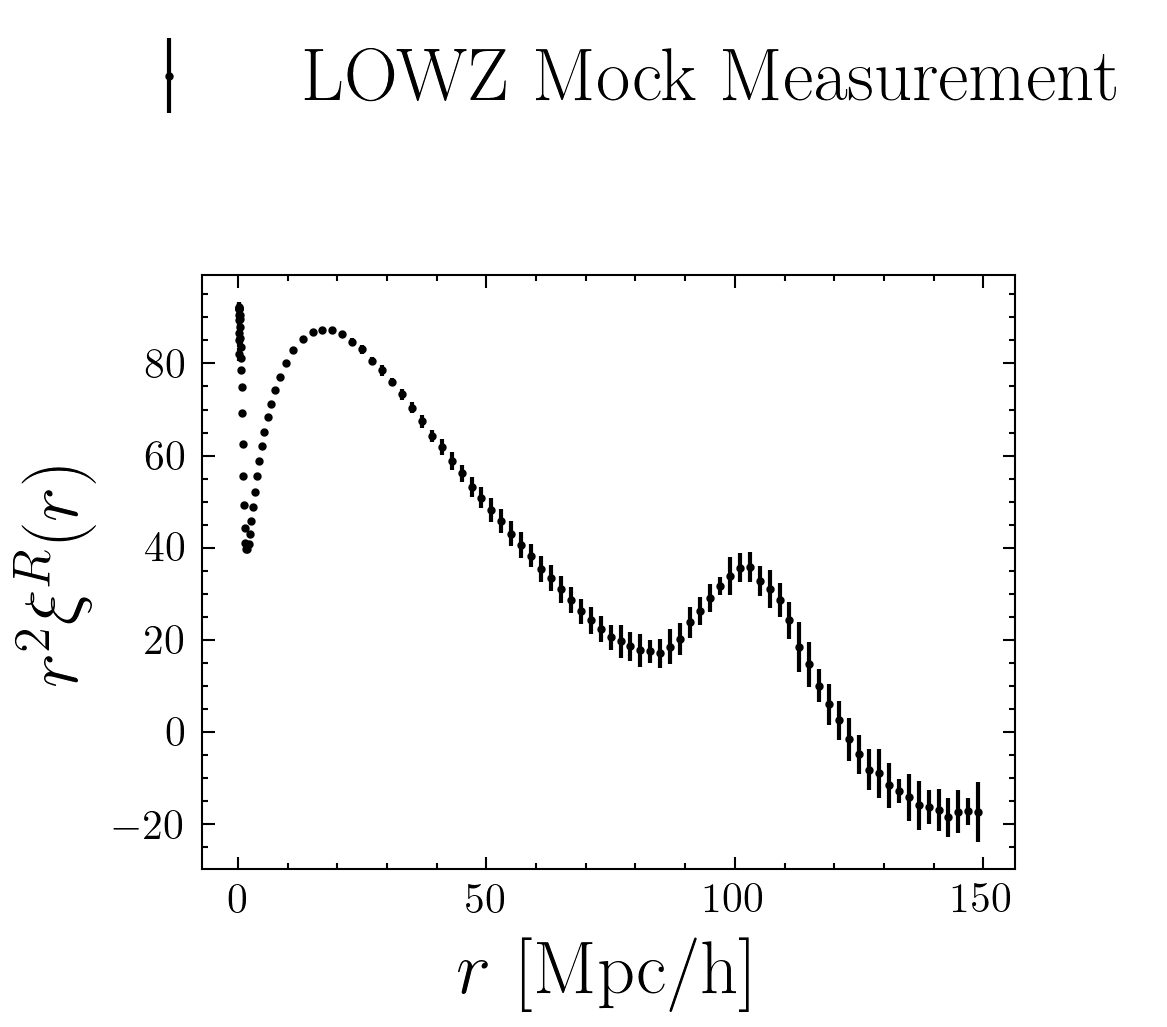
Machine Learning as a solution to
- Non-linearities Produce accurate predictions based on N-body simulations
- Non-Gaussianity Extract cosmological information at the field level
Cosmology =
\{\vec{c}\}
Main Assumptions
- Galaxies don't impact dark matter clustering
- Number of galaxies depends on halo mass only
- We don't know the Initial Conditions
- Data is very high dimensional
- Large number of parameters to constrain
- N-body sims extremely slow to run! (Sampling parameter space > O(10^6) calls)
Cosmology =
Galaxy =
\{\vec{c}\}
\{\vec{g}\}
\Omega_M
P(\vec{c}|\vec{D})
?
Summarise the data
\mathcal{O}(100)
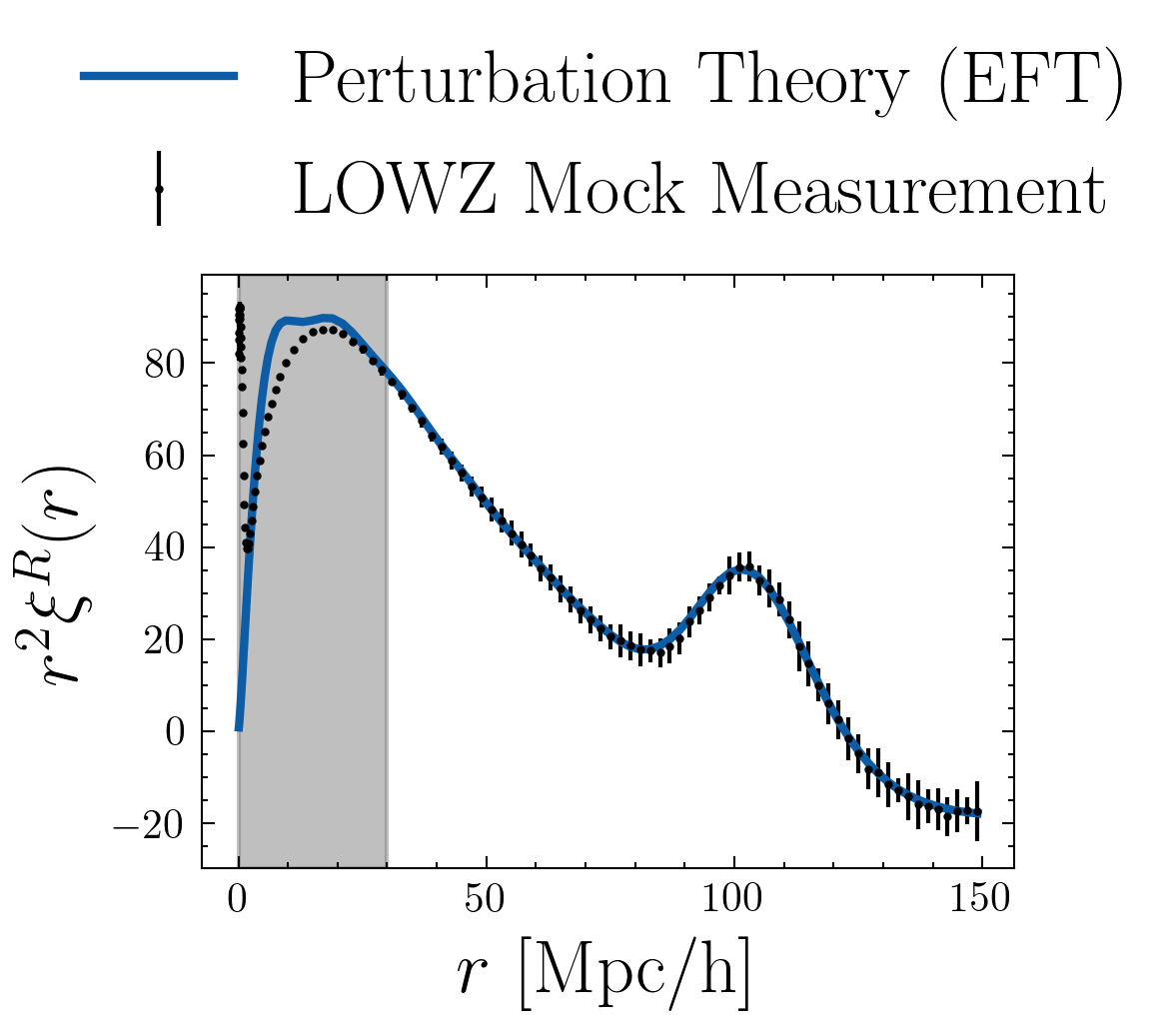
N-body simulations
\xi_{gg} = f(\vec{c}, \vec{g}, z)
\mathcal{O}(10^5)
Likelihood evaluations
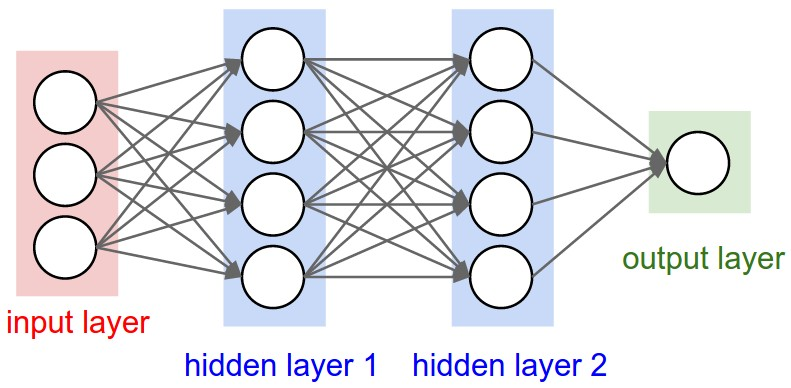
Credit: https://cs231n.github.io/convolutional-networks/
\hat{\xi}(r)
\mathcal{L} = \frac{1}{n} \sum |\hat{\xi}(r) - \xi(r)|
\Omega_m
r
\Omega_\Lambda
...
What to emulate?
- Flexibility: Vary galaxy tracers, and their cross-correlations. Marginalising over g requires flexible g!
-
1% accuracy1-sigma accuracy:- Emulator only as good as data used for training
- Model clustering and mapping between real and redshift space separately
\xi_{hh}^S = \red{F}(\blue{\xi_{hh}^R(r|\vec{c})}, \blue{v^{i}_{hh}(r|\vec{c})})
\xi_{gg}^S(\vec{s}|\vec{c},\vec{g},z) = \red{\mathcal{G}}(\blue{\xi_{hh}^S}(\vec{s}|\vec{c},z), \vec{g})
Neural Net
Analytical
1+\xi^S(s_\perp, s_\parallel) = \int dr_\parallel \left(1 + \blue{\xi^R(r)}\right) \red{\mathcal{P}(v_\parallel=s_\parallel-r_\parallel|r_\perp, r_\parallel)}
\blue{\xi^R(r)}
\xi^S(s_\perp, s_\parallel)
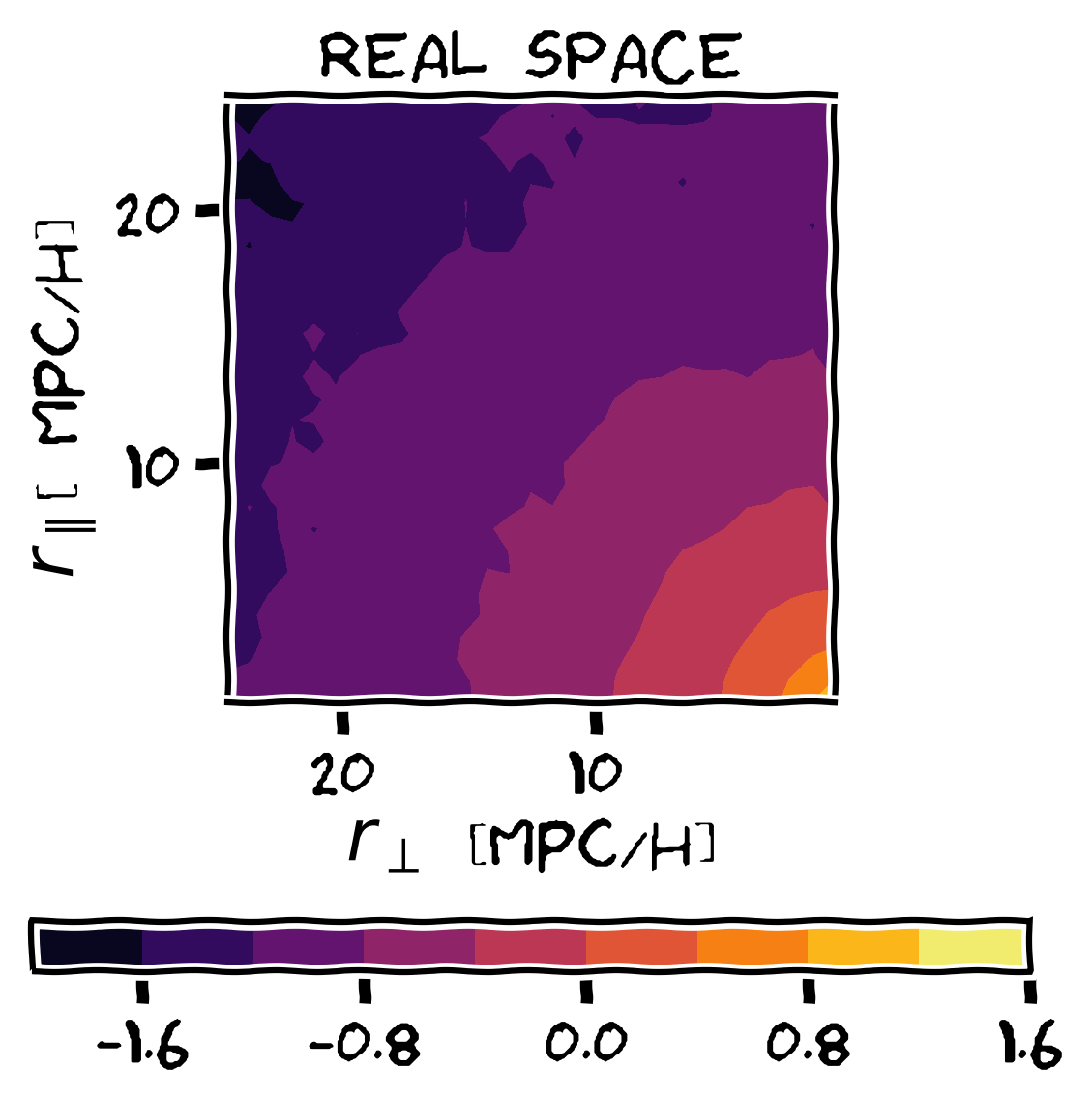
Cosmology =
\{\vec{c}\}
\vec{c}_i
Neural Network Emulator
\vec{c}, \mathrm{redshift}, M_h
\xi^R_{hh}(r|M_h)
v_{hh}(r|M_h)
1) Very fast -> MCMC
2) Halo-Galaxy mapping modelled very accurately
3) Allows for flexible implementations of Halo-Galaxy connection
4) Modelling RSD through the Streaming Model simplifies the functions the emulator needs to learn
\xi^R_{hh}(r|c_i, M_h)
v_{hh}(r|c_i, M_h)
Galaxy =
\{\vec{g}\}
\xi_{gg} \propto \int d M_h W(\vec{g}_j, M_h) \xi_{hh}(M_h)
r_\mathrm{min} = 0.1 \, h^{-1} \mathrm{Mpc}
r_\mathrm{min} = 3 \, h^{-1} \mathrm{Mpc}
r_\mathrm{min} = 20 \, h^{-1} \mathrm{Mpc}
Cosmology
Centrals
Satellites
How much information are we throwing away by summarising in two piont functions?
How much information are we throwing away by summarising the data?
\bar{\xi}(R_s)
R_s
Density-dependent clustering
1
1
1
2
2
4
5
5
5
3
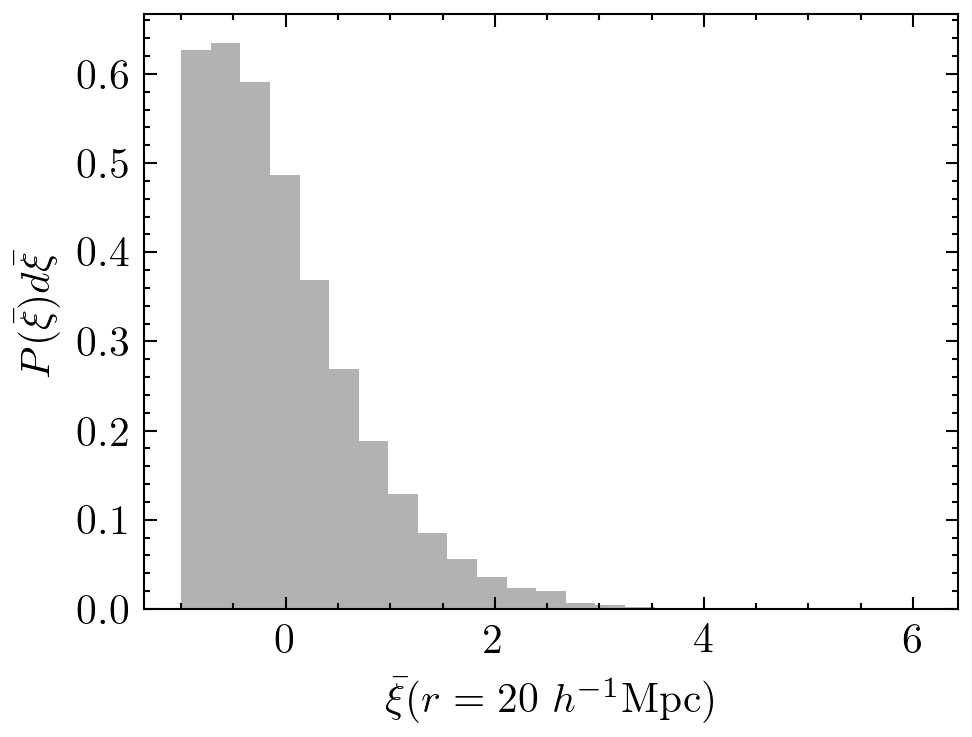
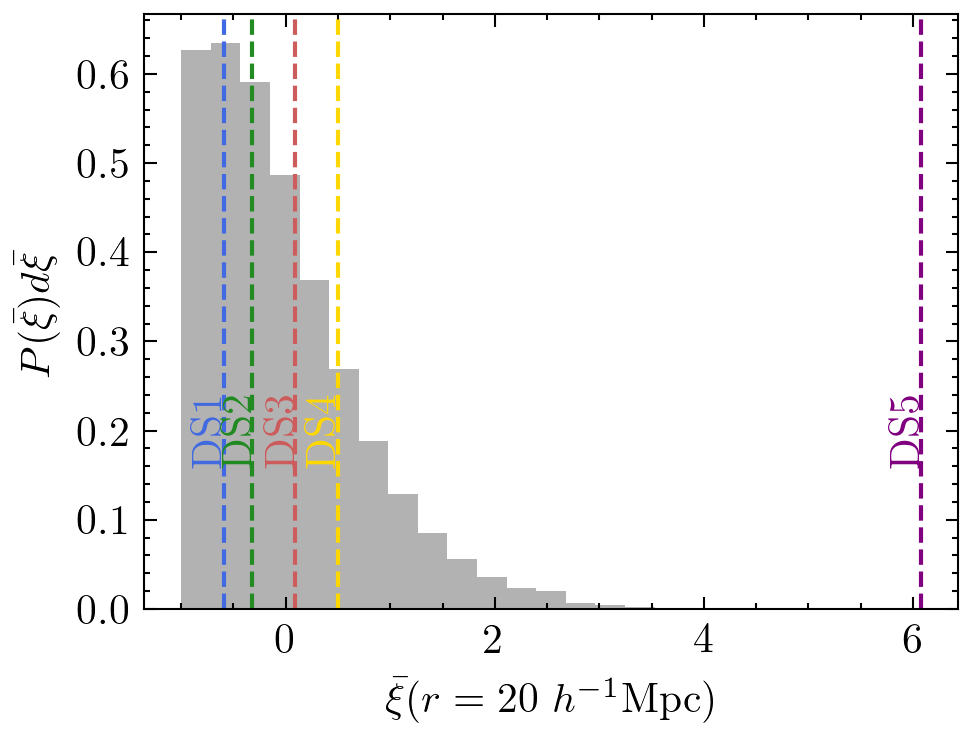
Clusters
r [h^{-1} \mathrm{Mpc}]
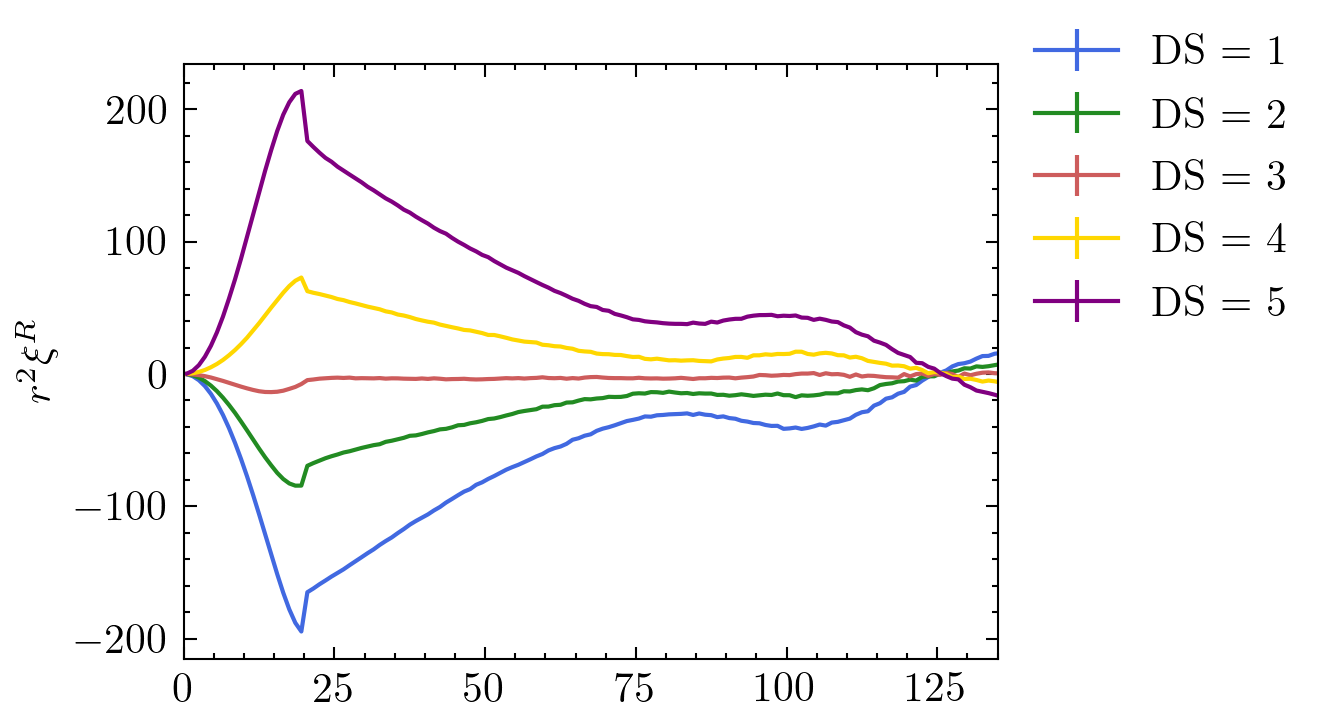
Voids
F_{\alpha \beta} = \mathbb{E} \left[\frac{\partial^2 \ln \mathcal{L}(x|\theta)}{\partial \theta_i \partial \theta_j} \right] = \frac{\partial S}{\partial \theta_\alpha} C^{-1} \frac{\partial S}{\partial \theta_\beta}
\delta \theta_\alpha \geq \left( F^{-1} \right)_{\alpha \alpha}
\frac{\partial \log \mathcal{L}(x|\theta)} {\partial \theta} = 0
\Omega_b
h
\sigma_8
n_s
M_\mathrm{min}
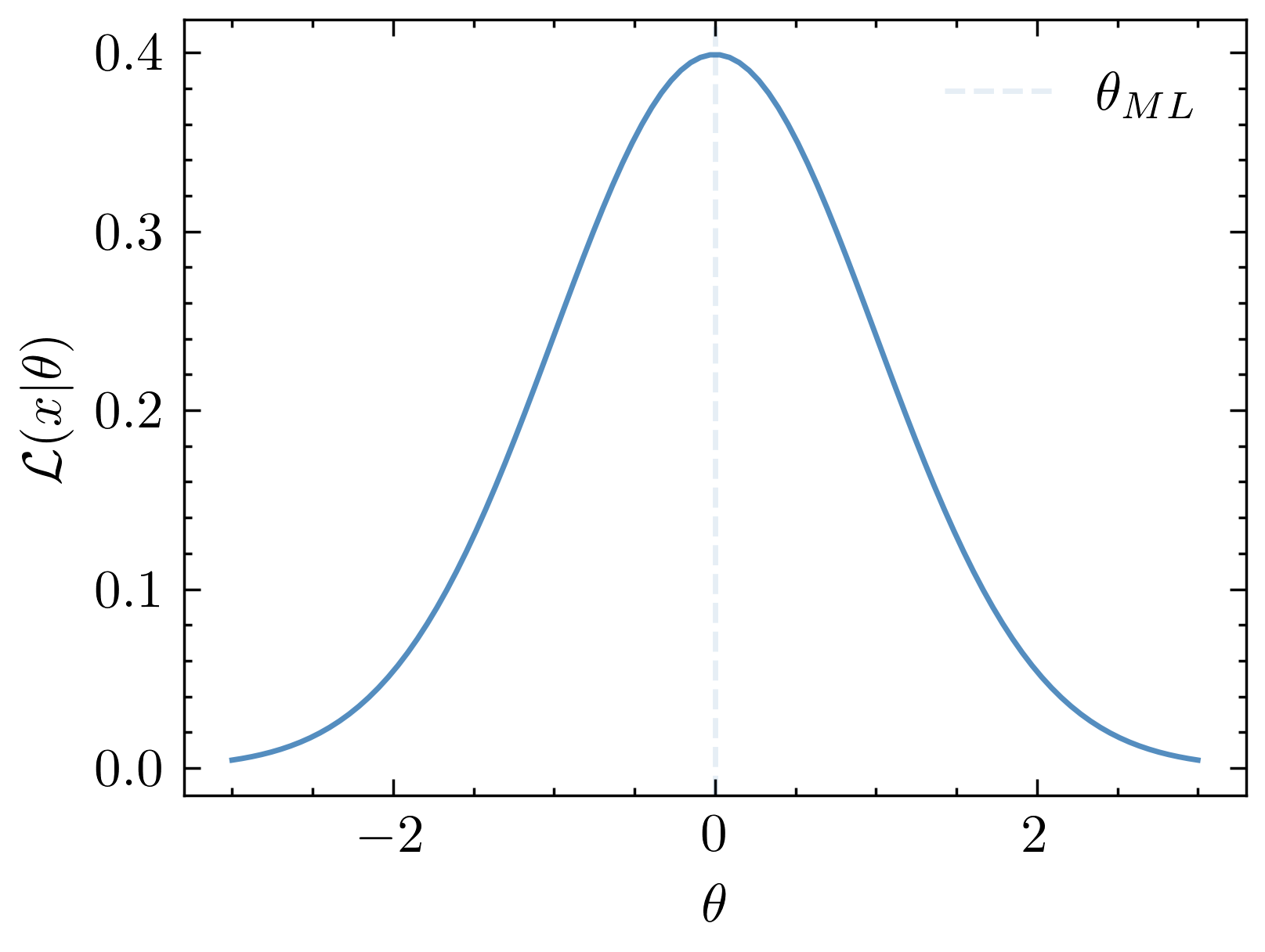
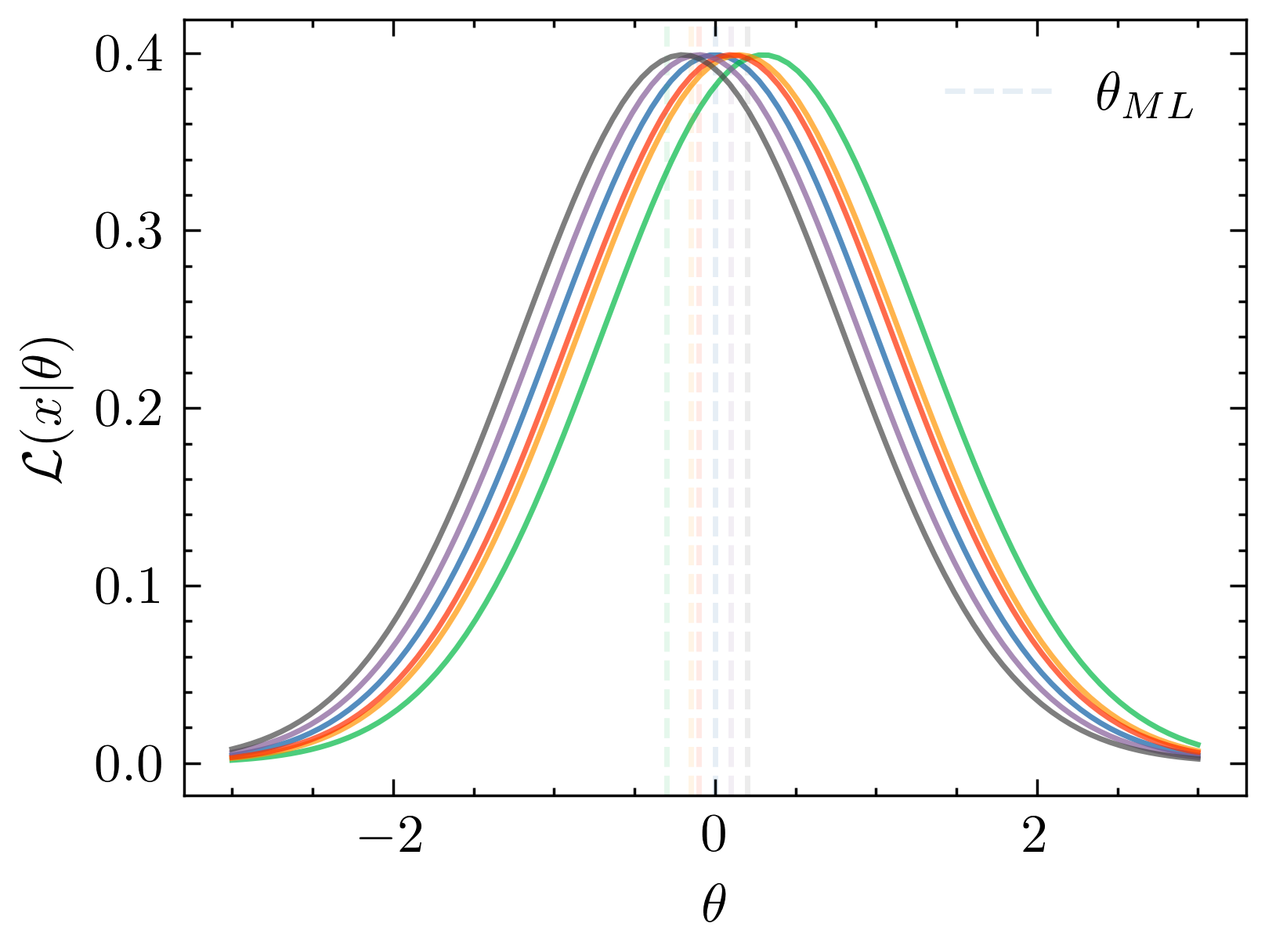
0.08
0.05
0.02
0.7
0.4
PRELIMINARY
0.85
0.80
1.1
1.0
0.9
3.5
0.9
3.0
\Omega_m
0.33
0.08
0.28
\Omega_b
h
\sigma_8
n_s
M_\mathrm{min}
0.03
0.07
0.4
0.7
0.8
0.86
0.87
1.06
0.87
3.0
3.5
\mathrm{2PCF}
\mathrm{DS}_{1+2+3+4+5} \, \, \mathrm{(z \, space)}
\mathrm{DS}_{1+2+3+4+5} \, \, \mathrm{(r \, space)}
\Omega_M
\Omega_\Lambda
\sigma_8
Input
x
Neural network
f
Representation
(Summary statistic)
r = f(x)
Output
o = g(r)
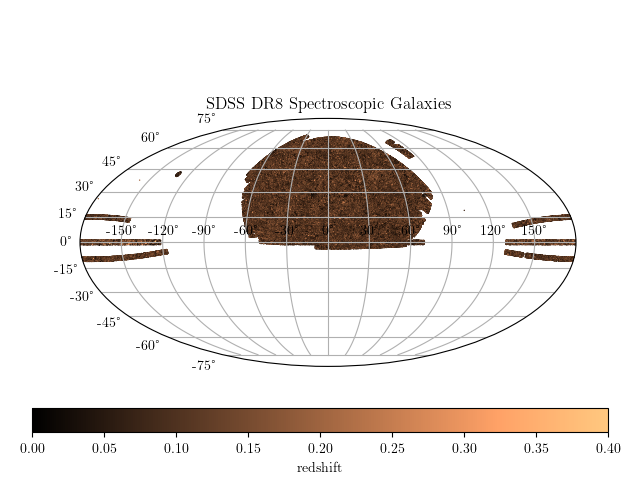
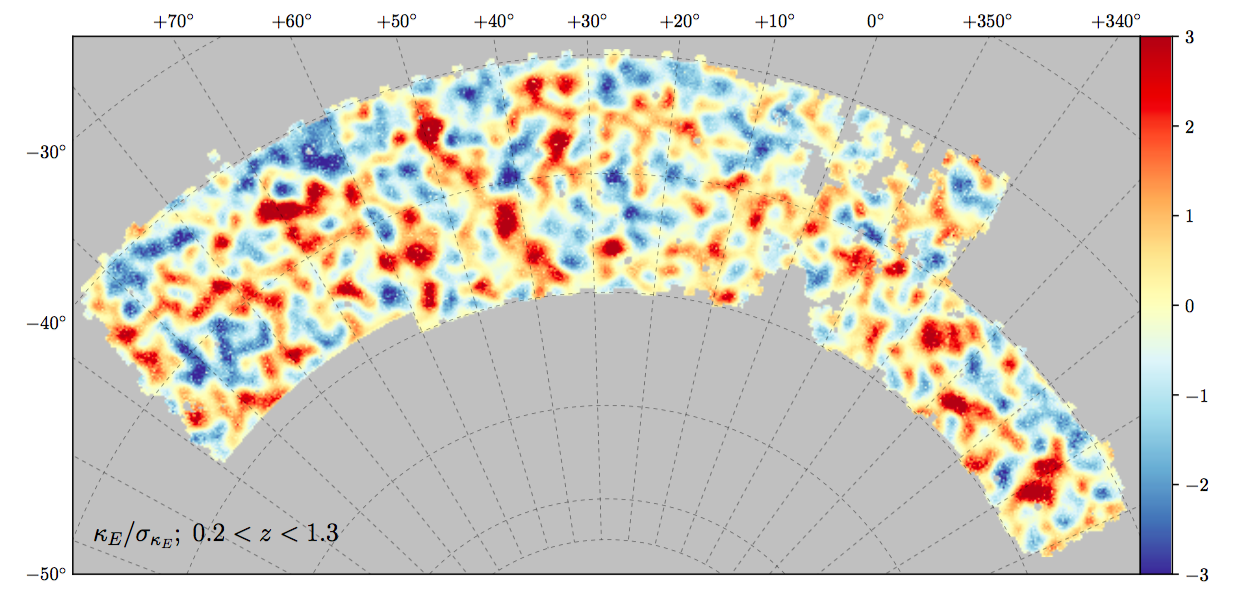
Increased interpretability through structured inputs
Modelling cross-correlations
ML and cosmology
- ML to accelerate non-linear predictions: allow MCMC sampling of non-linear scales
- Precision of future surveys: what and how we emulate will have an impact on cosmological constraints
- Can ML extract **all** the information that there is at the field-level in the non-linear regime?
- Compare data and simulations, point us to the missing pieces?
Copy of deck
By carol cuesta
