Large Deviations statistics of the cosmic log-density field
Cora Uhlemann
The evolution of the density field
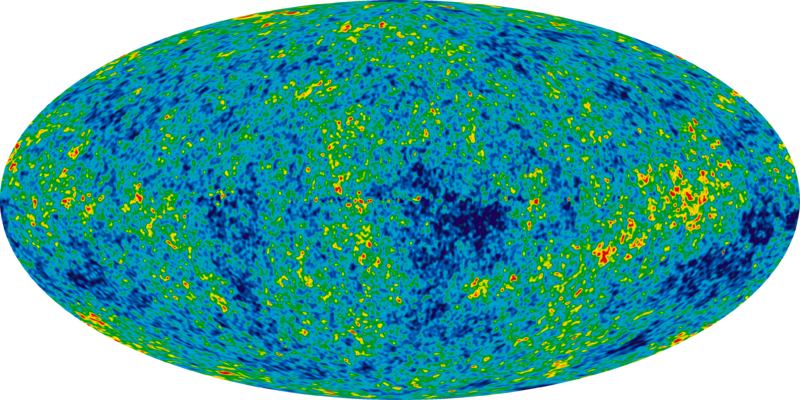
Initial
Gaussian density fluctuations
First two moments
Requires infinite number of moments
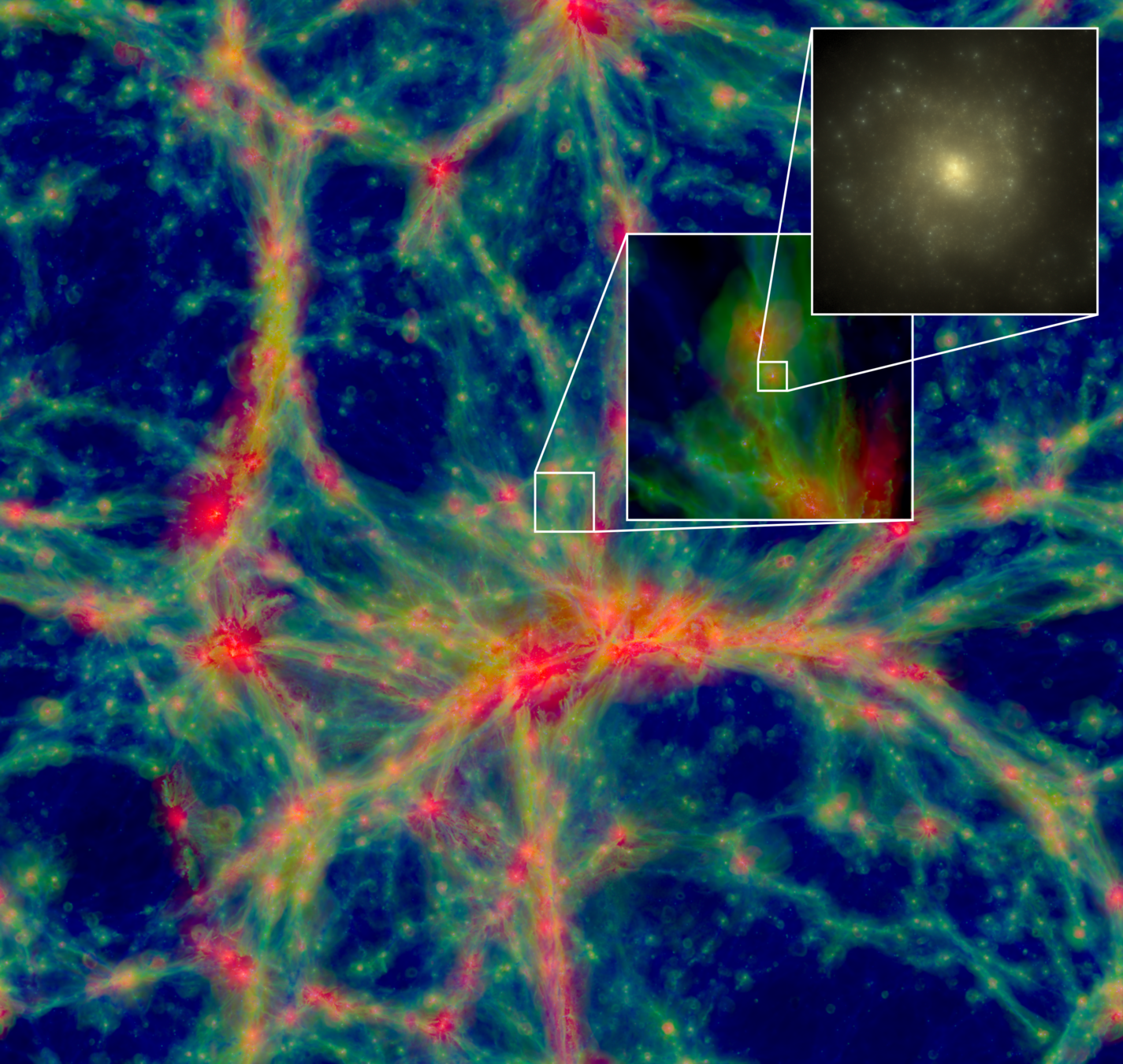
Gravity
Non-Gaussian
Barrier at 0!
Credit: S. Codis+16
Current approaches to describe the non-Gaussian field
- Perturbation theory : Needs perturbations to be small everywhere
- N-body simulations, solve the fully non-linear equations
Can we derive an analytical expression for the fully non-linear field from first principles?
Statistics of density in concentric spheres
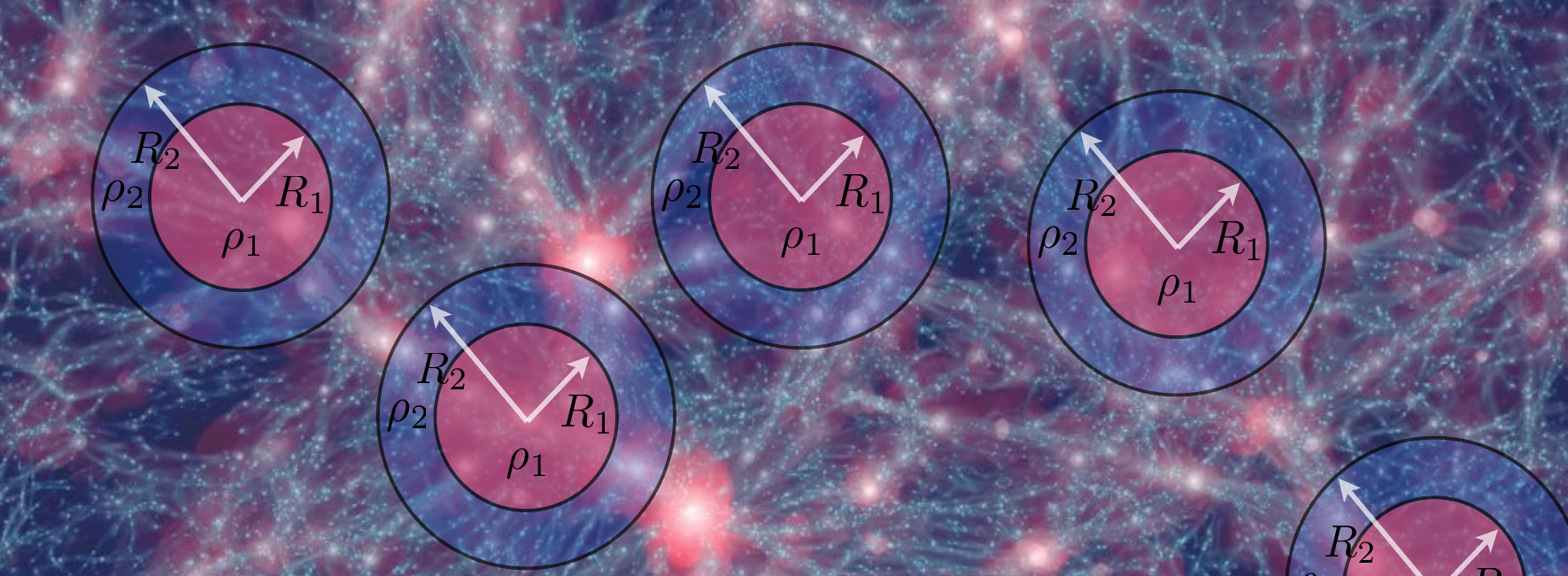
Only assumption : the variance of the field must be small inside the sphere
Large Deviations Principle + Spherical Collapse
Uhlemann '16
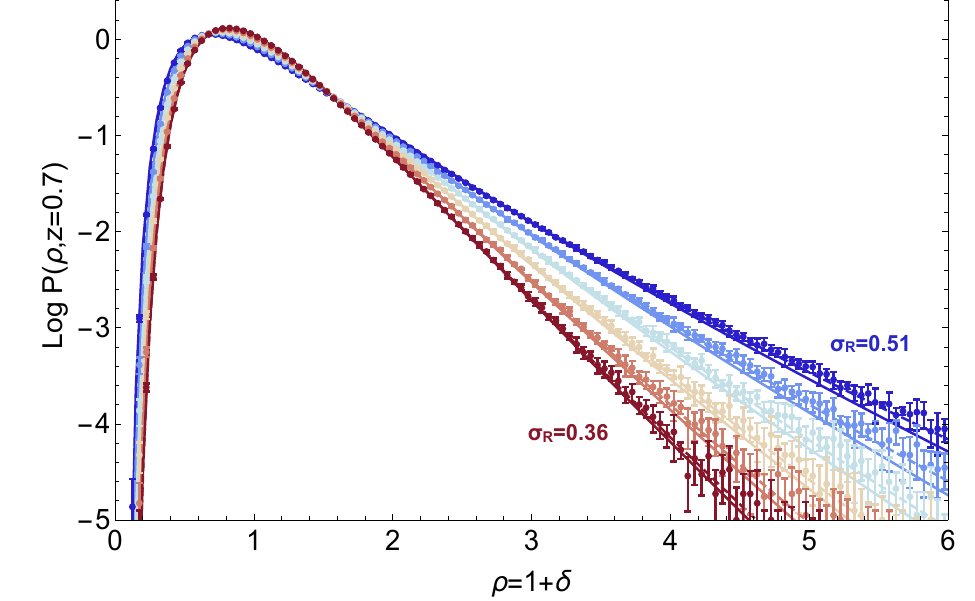
What is the most likely initial configuration the final density originated from?
Assumption: Spherical symmetry ensures the most likely path is given by spherical collapse dynamics
\int D[\tau]
Credit: S. Codis
What is the most likely one?
Valageas 2002
Large Deviations Theory
\lim_{\epsilon^2\to0} \epsilon^2 \log P_\epsilon (\tau) = - \psi (\tau)
Theory around probability families that fulfill:
P(\tau) \propto e^{-\psi(\tau)}
\lim_{\sigma^2\to0} \sigma^2 \log P(\tau) = - \psi (\tau)
Driving parameter
Rate Function
True for a Gaussian PDF
CONTRACTION PRINCIPLE If tau follows LDP:
\rho = F[\tau]
Family of (non-linear) mappings from tau to rho
\lim_{\sigma^2\to0} \sigma^2 \log P(\rho) = - \psi (\zeta ^{-1} (\rho))
Most likely mapping from tau to rho
Large deviations follow the most likely of the unlikely paths
\psi (\tau) = \frac{\tau^2}{\sigma^2}
\tau
\tau_\star = \zeta^{-1} (\rho _\star)
\psi_\star
P(\rho_\star) \propto e^{-\psi_\star}
i) Initial Gaussian random field
\sigma^2(R) = \frac{1}{(2\pi)^3} \int d^3 k P_{linear} (k) W^2(kR)
ii) Map the initial PDF into the final one assuming the most likely path given by spherical collapse dynamics
\rho = \zeta_\nu (\delta)
iii) Final PDF depends on:
P(\rho | \nu, P_{linear}, \sigma_{NL} (R,z))
Modifications of gravity
Growth of structure
Primordial non-Gaussianity
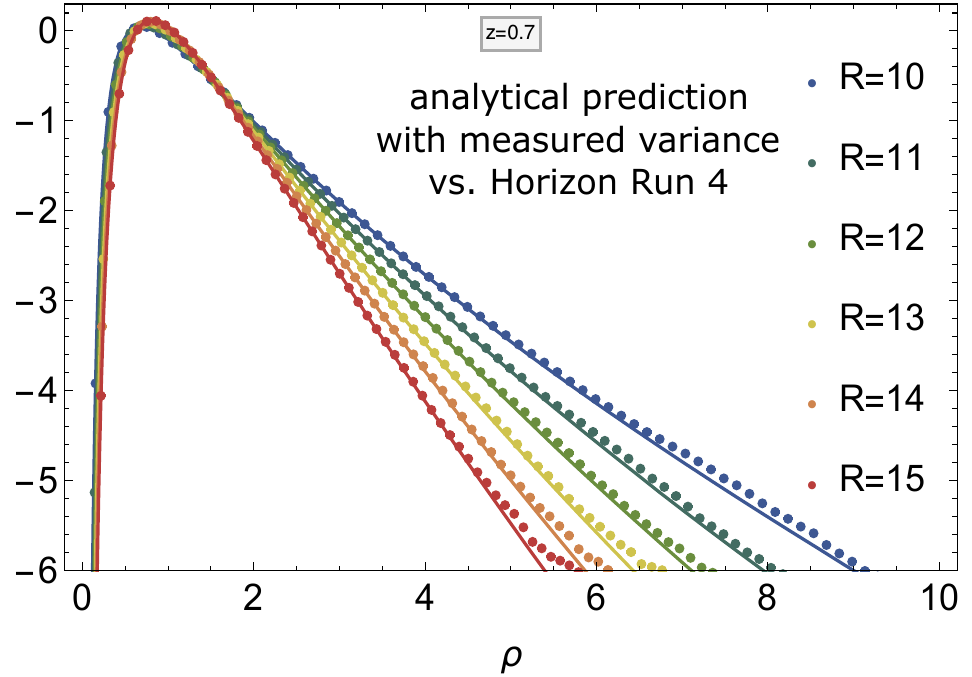
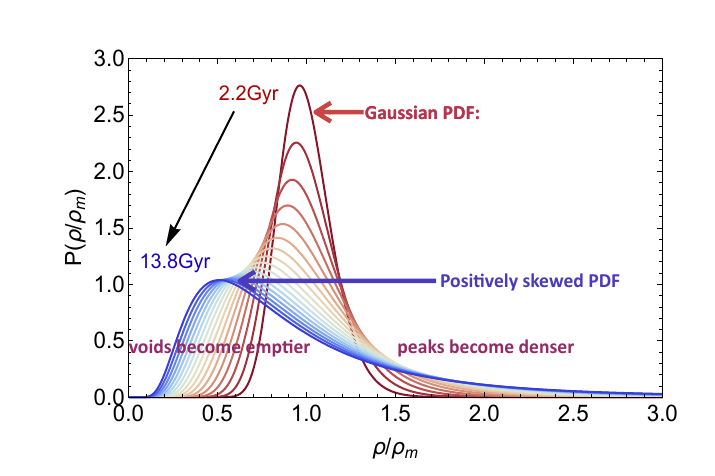
Main result
log(P(\rho))
- Fully analytical predictions for the density PDF in a sphere accurate at the percent level in the non-linear regime (data not used at the moment).
- Use the cosmological dependency to test gravity in the non linear regime.
- For density in spheres, the most likely dynamics is the one respecting the symmetry.
Summary
Group Meeting: large deviations
By carol cuesta
