\Omega_M
\Omega_\Lambda
\sigma_8
Input
x
Neural network
f
Representation
(Summary statistic)
r = f(x)
Output
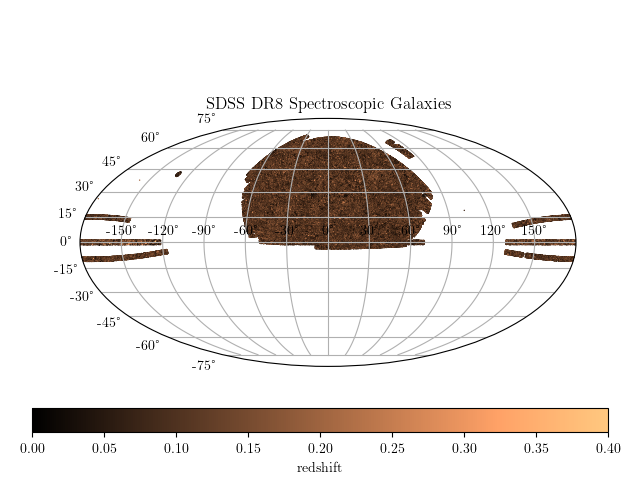
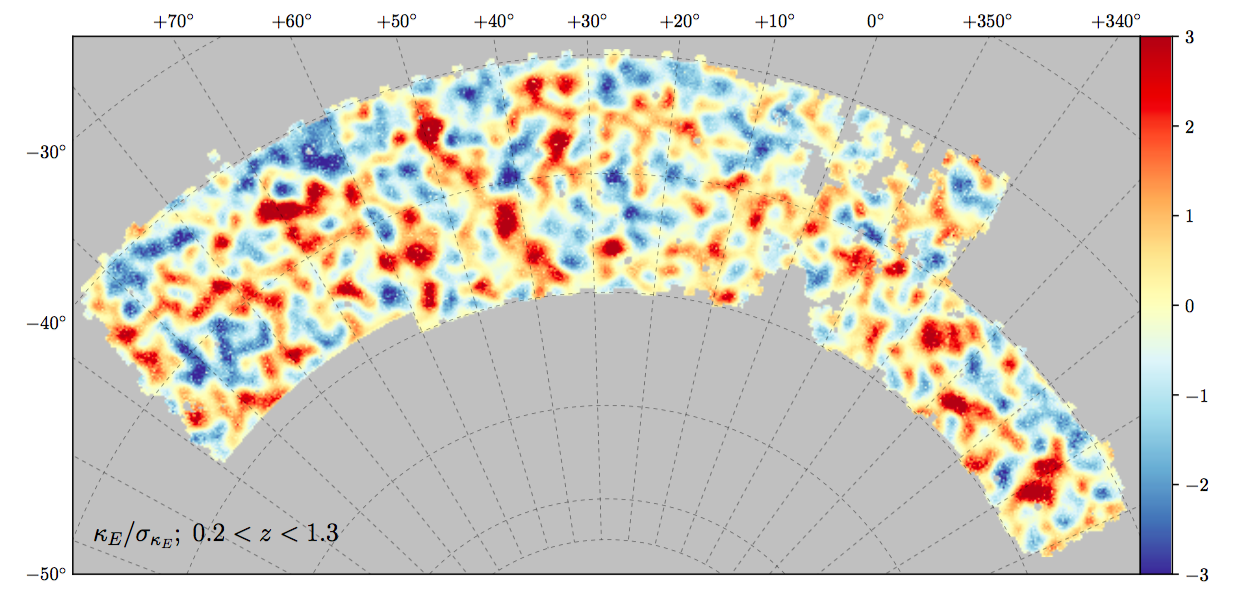
Modelling cross-correlations
P(\theta|x_\mathrm{obs})
Implicit likelihood inference with normalising flows
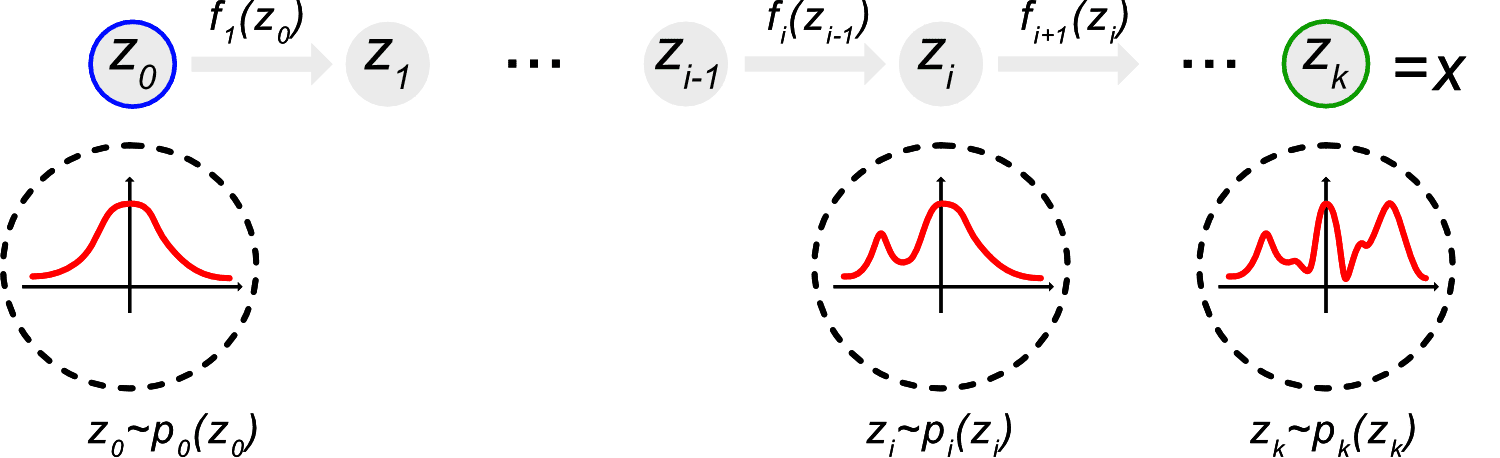
x = f(z), \, z = f^{-1}(x)
p(\mathbf{x}) = p_z(f^{-1}(\mathbf{x})) \left\vert \det J(f^{-1}) \right\vert
No assumptions on the likelihood (likelihoods rarely Gaussian!)
No expensive MCMC chains needed to estimate posterior





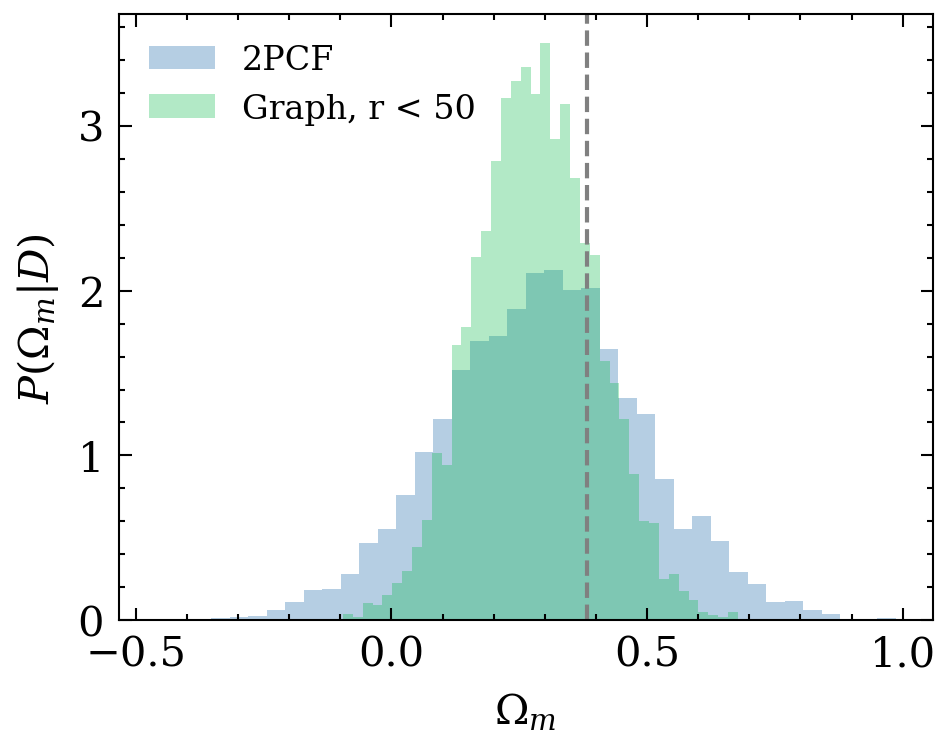
P(\mathcal{C}|\mathrm{GNN}(G))
\mathcal{L} = - \frac{1}{N} \sum_i \log\left(P(\mathcal{C}|\mathrm{GNN}(G))\right)
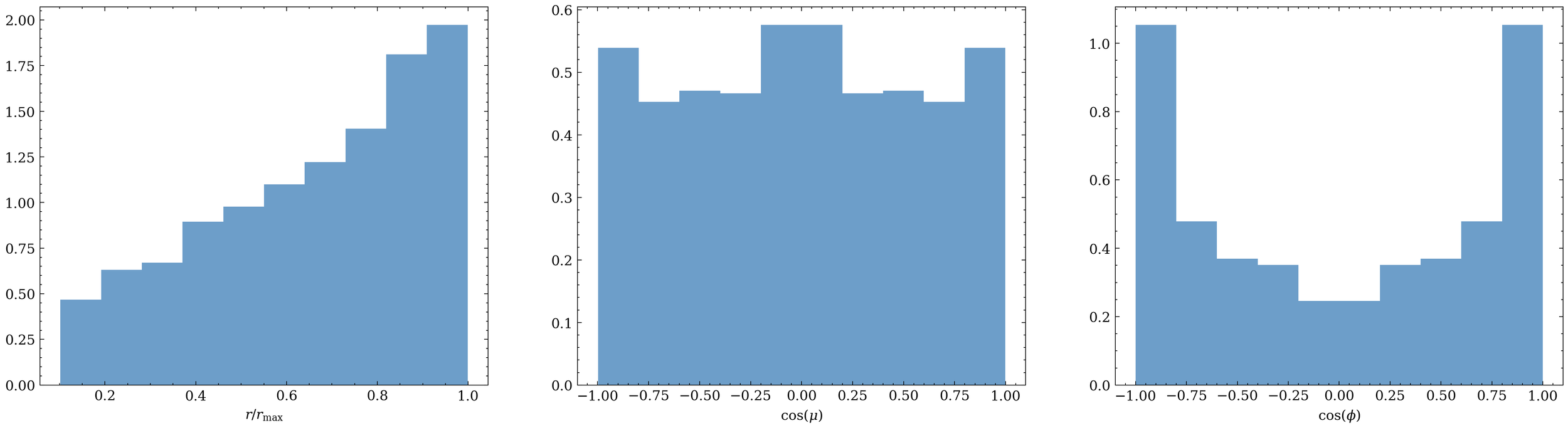
(r_{ij}, \theta_{ij}, \phi_{ij})
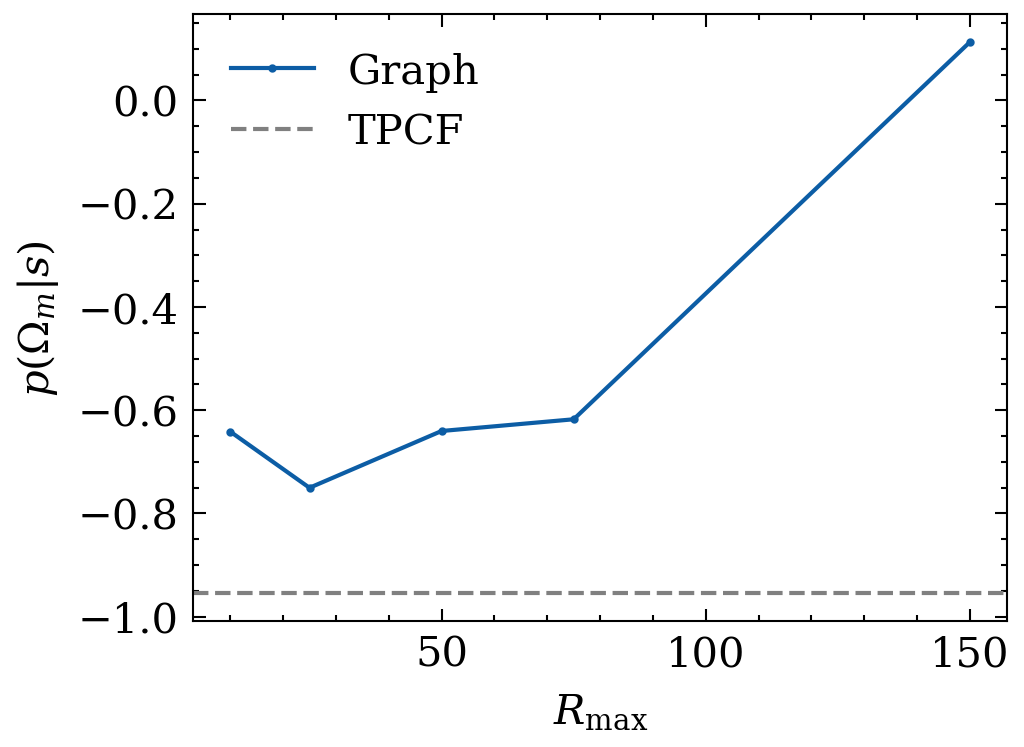
G(r_\mathrm{max})
Input
Output
Rotation and translation Invariant
Summarising with graph neural networks
\mathcal{G} = h^{L}_i, e^{L}_{ij} \rightarrow h^{L+1}_i, e^{L+1}_{ij}
e^{L+1}_{ij} = \phi_e(e^L_{ij}, h^L_i, h^L_j)
h^{L+1}_{i} = \phi_h( h^L_i, \mathcal{A}_j e^{L+1}_{ij})
S = \phi_s( \mathcal{A}_i h^L_i)
edge embedding
node embedding
summary statistic
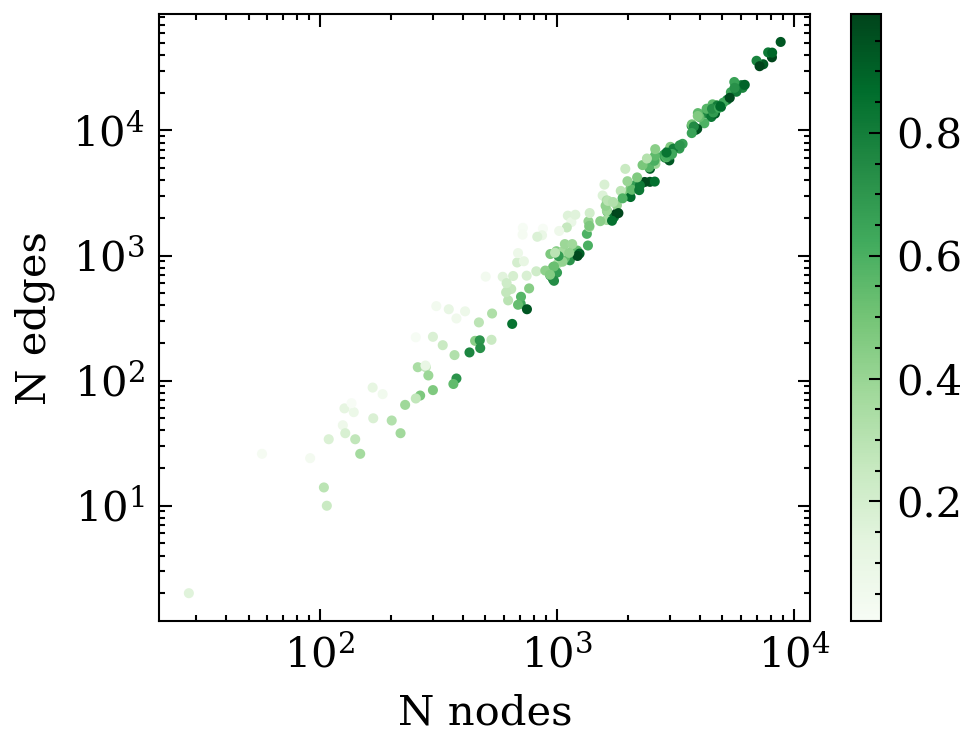
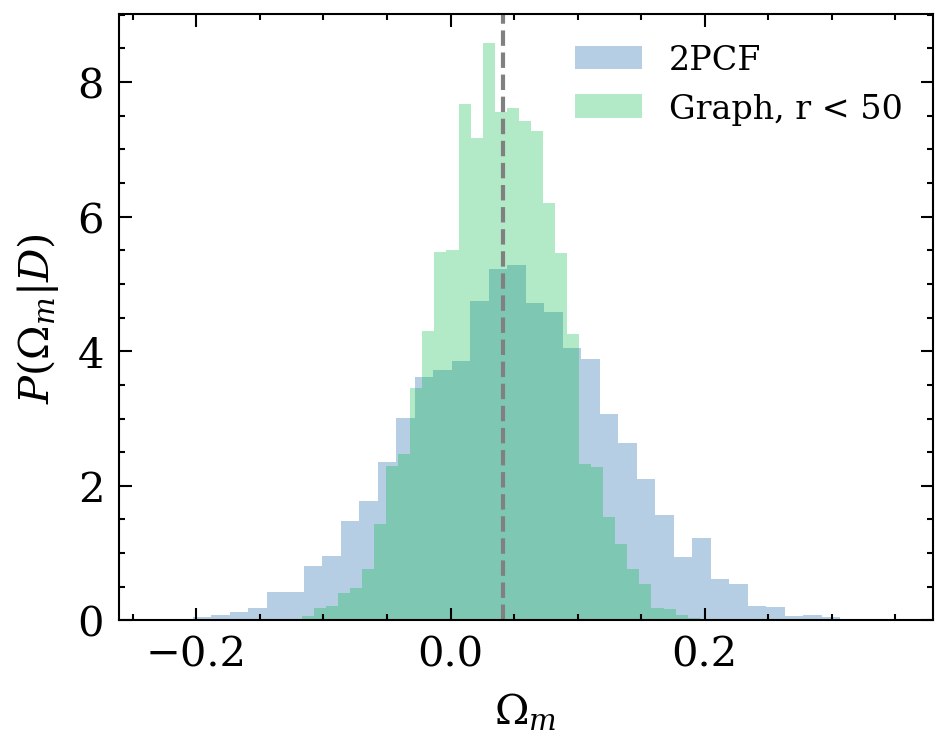
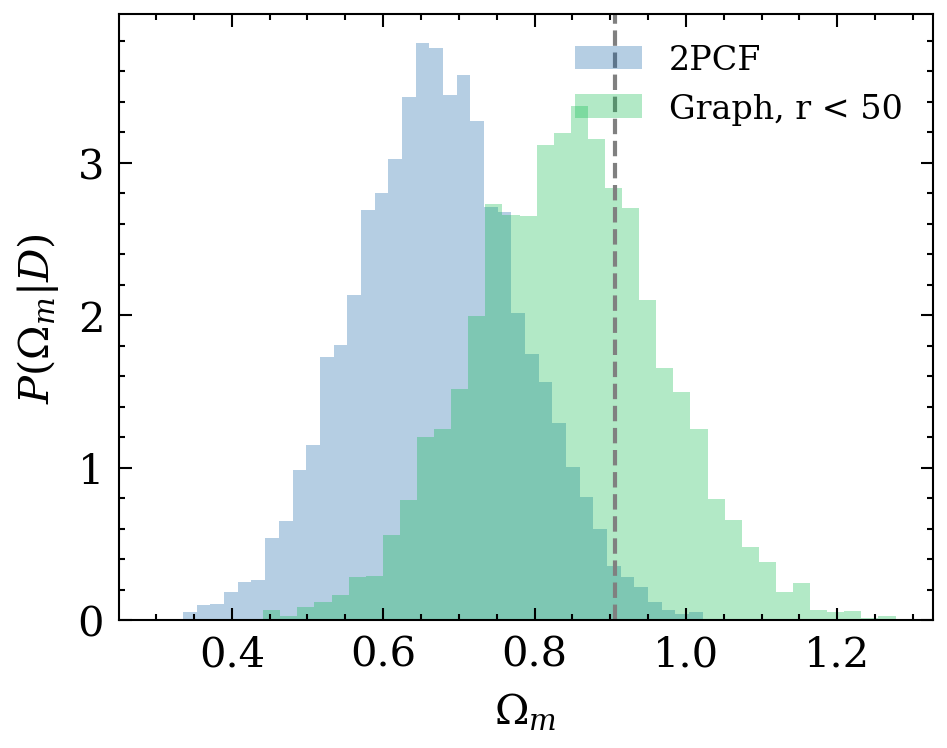
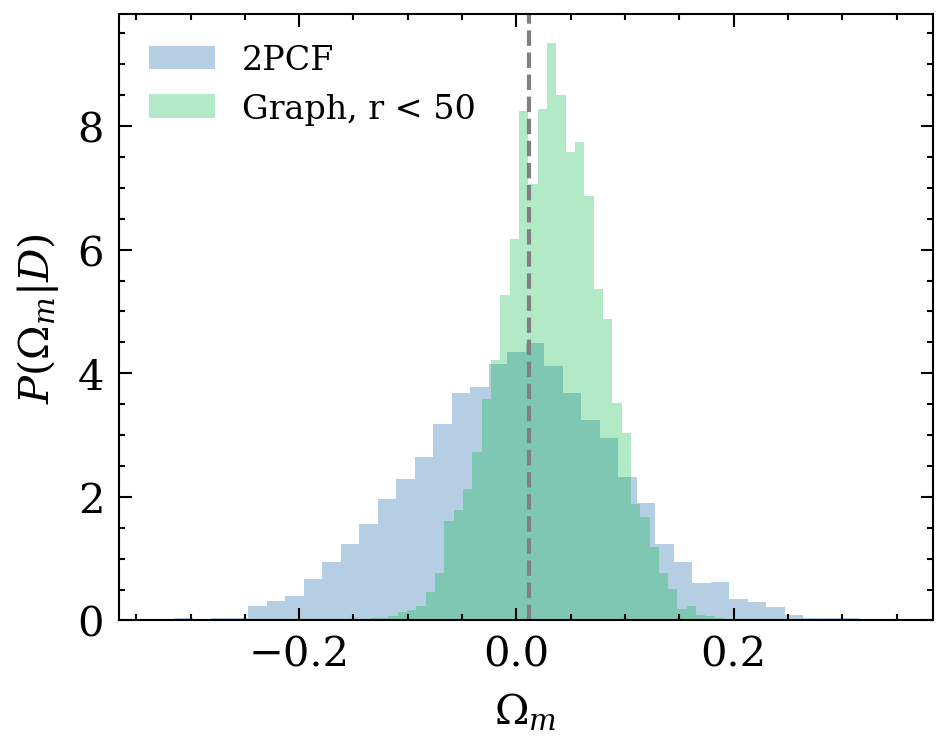
e^{L+1}_{ij} = \phi_e(e^L_{ij}, h^L_i, h^L_j)
h^{L+1}_{i} = \phi_h( h^L_i, \mathcal{A}_j e^{L+1}_{ij})
S = \phi_s( \mathcal{A}_i h^L_i)
edge embedding
node embedding
summary statistic
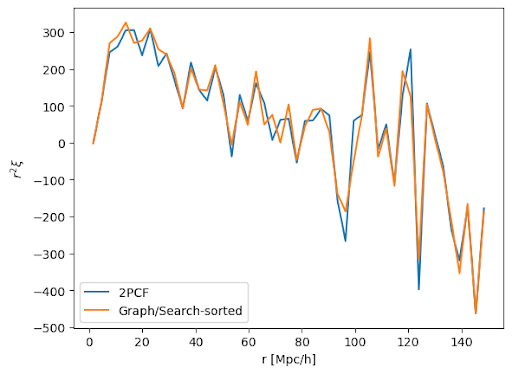
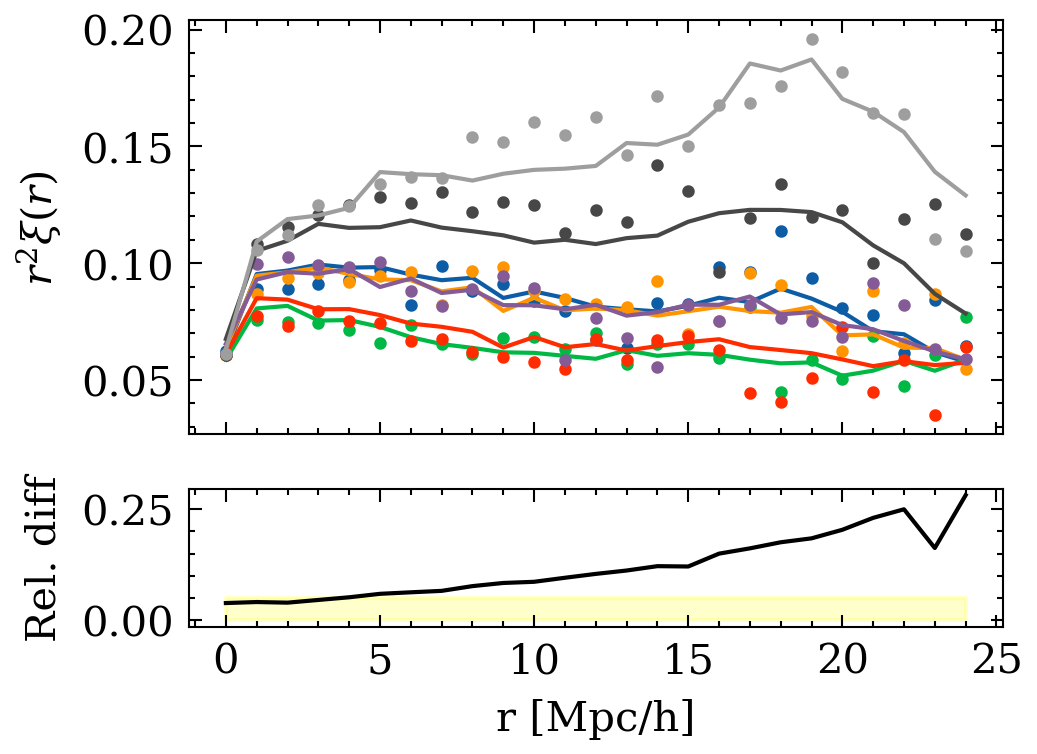
e^{L+1}_{ij} = \mathrm{searchsorted}(r_{ij})
h^{L+1}_{i} = \sum_j e^{L+1}_{ij}
S = \sum_i h^L_i
deck
By carol cuesta
deck
- 421



