Equivariant normalizing flows and their application to cosmology

Carolina Cuesta-Lazaro

 April 2022 - IAIFI JC

θ\theta
\theta

Simulated Data

Data

Prior

Posterior

xobsx_\mathrm{obs}
x_\mathrm{obs}
xx
x
P(θ∣xobs)P(\theta|x_\mathrm{obs})
P(\theta|x_\mathrm{obs})

Forwards

Inverse

θ=ΩM,σ8\theta = {\Omega_M, \sigma_8}
\theta = {\Omega_M, \sigma_8}

Cosmological parameters

EARLY UNIVERSE

LATE UNIVERSE

Normalizing flows: Generative models and  density estimators

xx
x
zz
z
xx
x
zz
z

VAE,GAN ...

Gaussianization

Data space

Latent space

x=fϕ(z)x = \green{f_\phi}(z)
x = \green{f_\phi}(z)

Image Credit: https://lilianweng.github.io/posts/2018-10-13-flow-models/

L(D)=−1∣D∣∑x∈Dlog⁡p(x)\mathcal{L}(\mathcal{D}) = - \frac{1}{\vert\mathcal{D}\vert}\sum_{\mathbf{x} \in \mathcal{D}} \log p(\mathbf{x})
\mathcal{L}(\mathcal{D}) = - \frac{1}{\vert\mathcal{D}\vert}\sum_{\mathbf{x} \in \mathcal{D}} \log p(\mathbf{x})

Maximize the data likelihood

NeuralNet

p(x)=pz(z)∣det⁡dzdx∣=pz(f−1(x))∣det⁡df−1dx∣p(\mathbf{x}) = p_z(\mathbf{z}) \left\vert \det \dfrac{d \mathbf{z}}{d \mathbf{x}} \right\vert = p_z(f^{-1}(\mathbf{x})) \left\vert \det \dfrac{d f^{-1}}{d \mathbf{x}} \right\vert
p(\mathbf{x}) = p_z(\mathbf{z}) \left\vert \det \dfrac{d \mathbf{z}}{d \mathbf{x}} \right\vert = p_z(f^{-1}(\mathbf{x})) \left\vert \det \dfrac{d f^{-1}}{d \mathbf{x}} \right\vert

f must be invertible

J efficient to compute 

1-D

n-D

p(x)=pz(f−1(x))∣det⁡J(f−1)∣p(\mathbf{x}) = p_z(f^{-1}(\mathbf{x})) \left\vert \det J(f^{-1}) \right\vert
p(\mathbf{x}) = p_z(f^{-1}(\mathbf{x})) \left\vert \det J(f^{-1}) \right\vert
x=f(z), z=f−1(x)x = f(z), \, z = f^{-1}(x)
x = f(z), \, z = f^{-1}(x)
p(x)=pz(z)∣det⁡dzdx∣p(\mathbf{x}) = p_z(\mathbf{z}) \left\vert \det \dfrac{d \mathbf{z}}{d \mathbf{x}} \right\vert
p(\mathbf{x}) = p_z(\mathbf{z}) \left\vert \det \dfrac{d \mathbf{z}}{d \mathbf{x}} \right\vert
p(x∣θ)=pz(f−1(x∣θ))∣det⁡J(f−1∣θ)∣p(\mathbf{x}|\theta) = p_z(f^{-1}(\mathbf{x}|\theta)) \left\vert \det J(f^{-1}|\theta) \right\vert
p(\mathbf{x}|\theta) = p_z(f^{-1}(\mathbf{x}|\theta)) \left\vert \det J(f^{-1}|\theta) \right\vert

Equivariance

f(Gx)=Gf(x)f(\mathcal{G} x) = \mathcal{G} f(x)
f(\mathcal{G} x) = \mathcal{G} f(x)
G\mathcal{G}
\mathcal{G}
G\mathcal{G}
\mathcal{G}
ff
f
G\mathcal{G}
\mathcal{G}

Invariance

f(Gx)=f(x)f(\mathcal{G}x) = f(x)
f(\mathcal{G}x) = f(x)
ff
f

Equivariant

pX(Gx)=pZ(f(Gx))∣det⁡Jf(Gx))∣p_X(\mathcal{G}\mathbf{x}) = p_Z(f(\mathcal{G}\mathbf{x})) |\det J_f(\mathcal{G}\mathbf{x}))|
p_X(\mathcal{G}\mathbf{x}) = p_Z(f(\mathcal{G}\mathbf{x})) |\det J_f(\mathcal{G}\mathbf{x}))|

Invariant

ff
f
p(x)p(x)
p(x)
=pZ(Gf(x))∣det⁡GJf(x))∣= p_Z(\mathcal{G}f(\mathbf{x})) |\det \mathcal{G} J_f(\mathbf{x}))|
= p_Z(\mathcal{G}f(\mathbf{x})) |\det \mathcal{G} J_f(\mathbf{x}))|
=pZ(f(x))∣det⁡Jf(x))∣= p_Z(f(\mathbf{x})) |\det J_f(\mathbf{x}))|
= p_Z(f(\mathbf{x})) |\det J_f(\mathbf{x}))|

Equivariant

ff
f

Invariant

pZp_Z
p_Z

Challenge: Expressive + Invertible + Equivariant

1. Continuous time Normalizing flows

ODE solutions are invertible!

z=x+∫01ϕ(x(t))dt\mathbf{z} = \mathbf{x} + \int_0^1 \phi(\mathbf{x}(t)) dt
\mathbf{z} = \mathbf{x} + \int_0^1 \phi(\mathbf{x}(t)) dt
x=z+∫10ϕ(x(t))dt\mathbf{x} = \mathbf{z} + \int_1^0 \phi(\mathbf{x}(t)) dt
\mathbf{x} = \mathbf{z} + \int_1^0 \phi(\mathbf{x}(t)) dt
z = odeint(self.phi, x, [0, 1])

torchdiffeq

log⁡pX(x)=log⁡pZ(z)+∫01Tr Jϕ(x(t))dt\log p_X(\mathbf{x}) = \log p_Z(\mathbf{z}) + \int_0^1 \mathrm{Tr }\, J _{\phi}(\mathbf{x}(t)) dt
\log p_X(\mathbf{x}) = \log p_Z(\mathbf{z}) + \int_0^1 \mathrm{Tr }\, J _{\phi}(\mathbf{x}(t)) dt

solving the ODE might introduce error in estimating p(x)

Image Credit: https://arxiv.org/abs/1810.01367

x=z+∫10ϕ(x(t))dt\mathbf{x} = \mathbf{z} + \int_1^0 \phi(\mathbf{x}(t)) dt
\mathbf{x} = \mathbf{z} + \int_1^0 \phi(\mathbf{x}(t)) dt
z=x+∫01ϕ(x(t))dt\mathbf{z} = \mathbf{x} + \int_0^1 \phi(\mathbf{x}(t)) dt
\mathbf{z} = \mathbf{x} + \int_0^1 \phi(\mathbf{x}(t)) dt

Equivariant? GNNs

mij=ϕe(hil,hjl,∣xil−xjl∣2)\mathbf{m}_{ij} =\phi_{e}\left(\mathbf{h}_{i}^{l}, \mathbf{h}_{j}^{l},\left|\mathbf{x}_{i}^{l}-\mathbf{x}_{j}^{l}\right|^{2}\right)
\mathbf{m}_{ij} =\phi_{e}\left(\mathbf{h}_{i}^{l}, \mathbf{h}_{j}^{l},\left|\mathbf{x}_{i}^{l}-\mathbf{x}_{j}^{l}\right|^{2}\right)
xil+1=xil+∑j≠i(xil−xjl)∣xil−xjl∣+1ϕx(mij)\mathbf{x}_{i}^{l+1} =\mathbf{x}_{i}^{l}+\sum_{j \neq i} \frac{(\mathbf{x}_{i}^{l}-\mathbf{x}_{j}^{l})}{|\mathbf{x}_{i}^{l}-\mathbf{x}_{j}^{l}| + 1} \phi_{x}\left(\mathbf{m}_{ij}\right)
\mathbf{x}_{i}^{l+1} =\mathbf{x}_{i}^{l}+\sum_{j \neq i} \frac{(\mathbf{x}_{i}^{l}-\mathbf{x}_{j}^{l})}{|\mathbf{x}_{i}^{l}-\mathbf{x}_{j}^{l}| + 1} \phi_{x}\left(\mathbf{m}_{ij}\right)
mi=∑j≠ieijmij\mathbf{m}_{i} = \sum_{j \not= i} e_{ij}\mathbf{m}_{ij}
\mathbf{m}_{i} = \sum_{j \not= i} e_{ij}\mathbf{m}_{ij}
hil+1=ϕh(hil,mi)\mathbf{h}_{i}^{l+1} =\phi_{h}\left(\mathbf{h}_{i}^l, \mathbf{m}_{i} \right)
\mathbf{h}_{i}^{l+1} =\phi_{h}\left(\mathbf{h}_{i}^l, \mathbf{m}_{i} \right)

1. Invertible but expressive

2. Equivariant to E(n)

x=z+∫10ϕ(x(t))dt\mathbf{x} = \mathbf{z} + \int_1^0 \phi(\mathbf{x}(t)) dt
\mathbf{x} = \mathbf{z} + \int_1^0 \phi(\mathbf{x}(t)) dt

E(n) equivariant normalizing flows

https://arxiv.org/abs/2105.09016

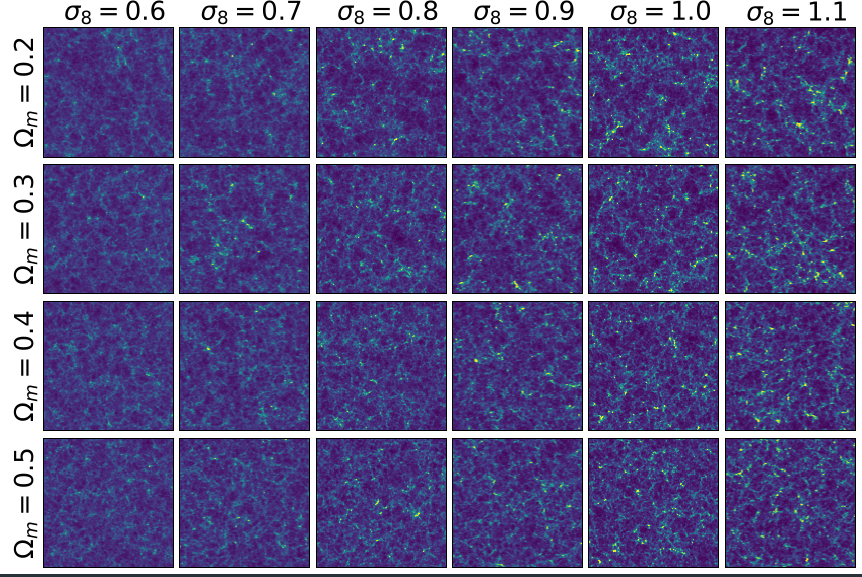
Cosmological simulations -> Millions of particles!

Solution: Density on mesh + Convolutions in Fourier space

https://arxiv.org/abs/2202.05282

∫T(r−r′)x(r′)dr′=F^−1(T^(k)x^(k))\int T(\mathbf{r} - \mathbf{r}^\prime) x(\mathbf{r}^\prime) d \mathbf{r}^\prime = \hat{F}^{-1} (\hat{T}(k) \hat{x}(\mathbf{k}))
\int T(\mathbf{r} - \mathbf{r}^\prime) x(\mathbf{r}^\prime) d \mathbf{r}^\prime = \hat{F}^{-1} (\hat{T}(k) \hat{x}(\mathbf{k}))
f=ψ(F^−1T^(k)F^x)f = \green{\psi} \left(\hat{F}^{-1} \red{\hat{T}(k)} \hat{F} x \right)
f = \green{\psi} \left(\hat{F}^{-1} \red{\hat{T}(k)} \hat{F} x \right)

1-D functions learned from data

https://arxiv.org/pdf/1906.04032.pdf

T^(k)\red{\hat{T}(k)}
\red{\hat{T}(k)}

Cubic splines (8 spline points)

ψ(x)\green{\psi(x)}
\green{\psi(x)}

Monotonic rational quadratic splines

(8 spline points)

Loss Function

Generative: Maximize likelihood

Discriminative: target the posterior

L=−1N∑ilog⁡p(xi∣θ)\mathcal{L} = -\frac{1}{N} \sum_i \log p(x_i|\theta)
\mathcal{L} = -\frac{1}{N} \sum_i \log p(x_i|\theta)
L=−1N∑ilog⁡p(θ∣xi)\mathcal{L} = -\frac{1}{N} \sum_i \log p(\theta|x_i)
\mathcal{L} = -\frac{1}{N} \sum_i \log p(\theta|x_i)
L=−1N∑i(log⁡p(xi∣θ)+log⁡p(θ)−log(p(θ))\mathcal{L} = -\frac{1}{N} \sum_i \left( \log p(x_i|\theta) + \log p(\theta) - log(p(\theta) \right)
\mathcal{L} = -\frac{1}{N} \sum_i \left( \log p(x_i|\theta) + \log p(\theta) - log(p(\theta) \right)
p(θ∣x)=p(x∣θ)p(θ)p(x)p(\theta|\mathbf{x}) = \frac{p(\mathbf{x}|\theta)p(\theta)}{p(\mathbf{x})}
p(\theta|\mathbf{x}) = \frac{p(\mathbf{x}|\theta)p(\theta)}{p(\mathbf{x})}

Gaussian Random Field:

The Power spectrum is an optimal summary statistic

Analytical likelihood

Flow likelihood

T^(k)=1aP(k)\hat{T}(k) = \frac{1}{a\sqrt{P(k)}}
\hat{T}(k) = \frac{1}{a\sqrt{P(k)}}
ψ(x)=ax\psi(x) = a x
\psi(x) = a x

Non-Gaussian N-body simulations

1. Inference

Non-Gaussian N-body simulations

2. Sampling

  • Can we quantify the full information content? Can normalizing flows extract all the information there is about cosmology?

 

  • Can the latent space be the initial conditions for the N-body sim?

 

  • Are current models to embed symmetries too constraining?

 

  • Model misspecification? 

 

  • Does dimensionality reduction help with interpretability?

 

 

deck

By carol cuesta

deck

  • 418

More from carol cuesta