Robust Simulation-Based Inference
Flatiron Institute
Institute for Advanced Studies
Carol(ina) Cuesta-Lazaro
We need to talk about your forward model...
\delta_\mathrm{ICs}
\delta_\mathrm{Obs}
Reconstructed
True
p(\delta_\mathrm{ICs}, \theta|\delta_\mathrm{Obs})
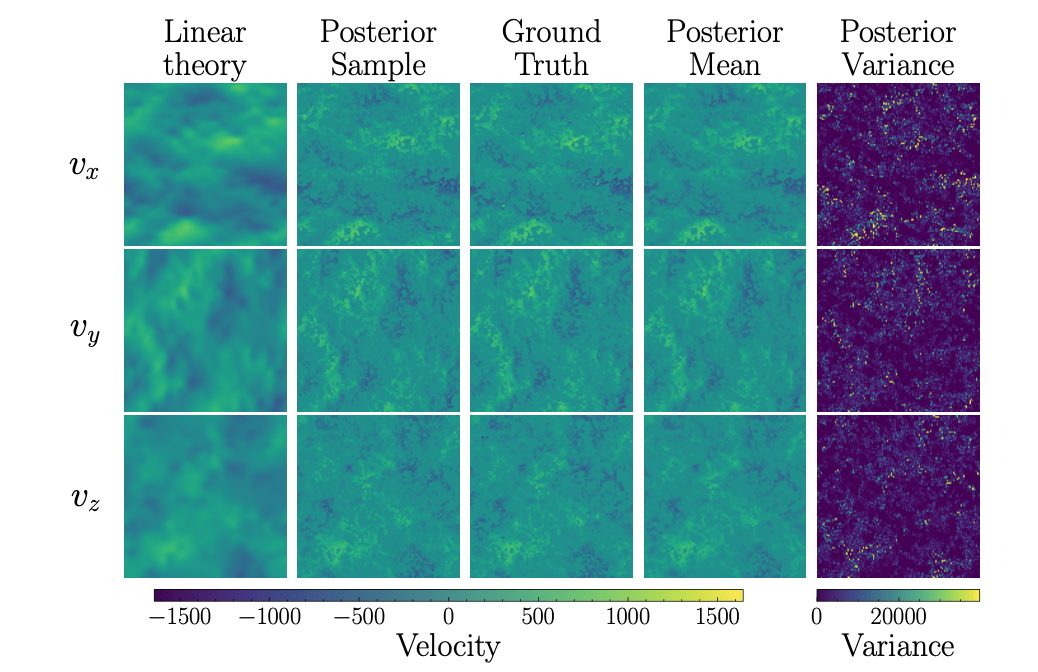
Galaxy Peculiar Velocity Reconstruction
Field-Level Inference
Cross-Correlations: FRBs x Galaxies
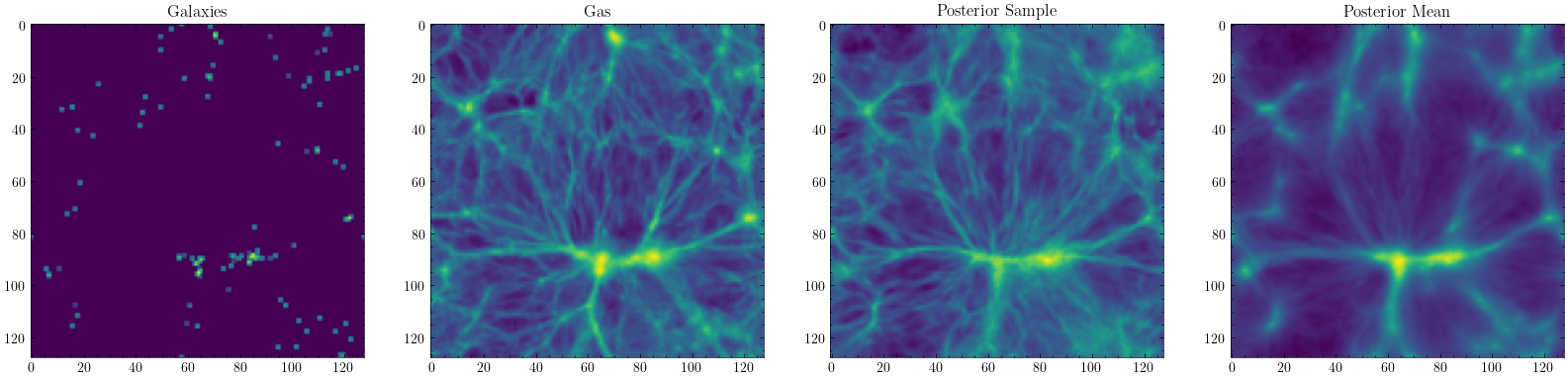
Galaxies
Linear
Galaxy Velocity
Reconstructed
Gas
Reconstructed
Carolina Cuesta-Lazaro Flatiron/IAS
Astrophysics proliferates Simulation-based Inference
on Simulations
Carolina Cuesta-Lazaro Flatiron/IAS
x^\mathcal{O}
x^\mathcal{S}
Simulated Data
Observed Data
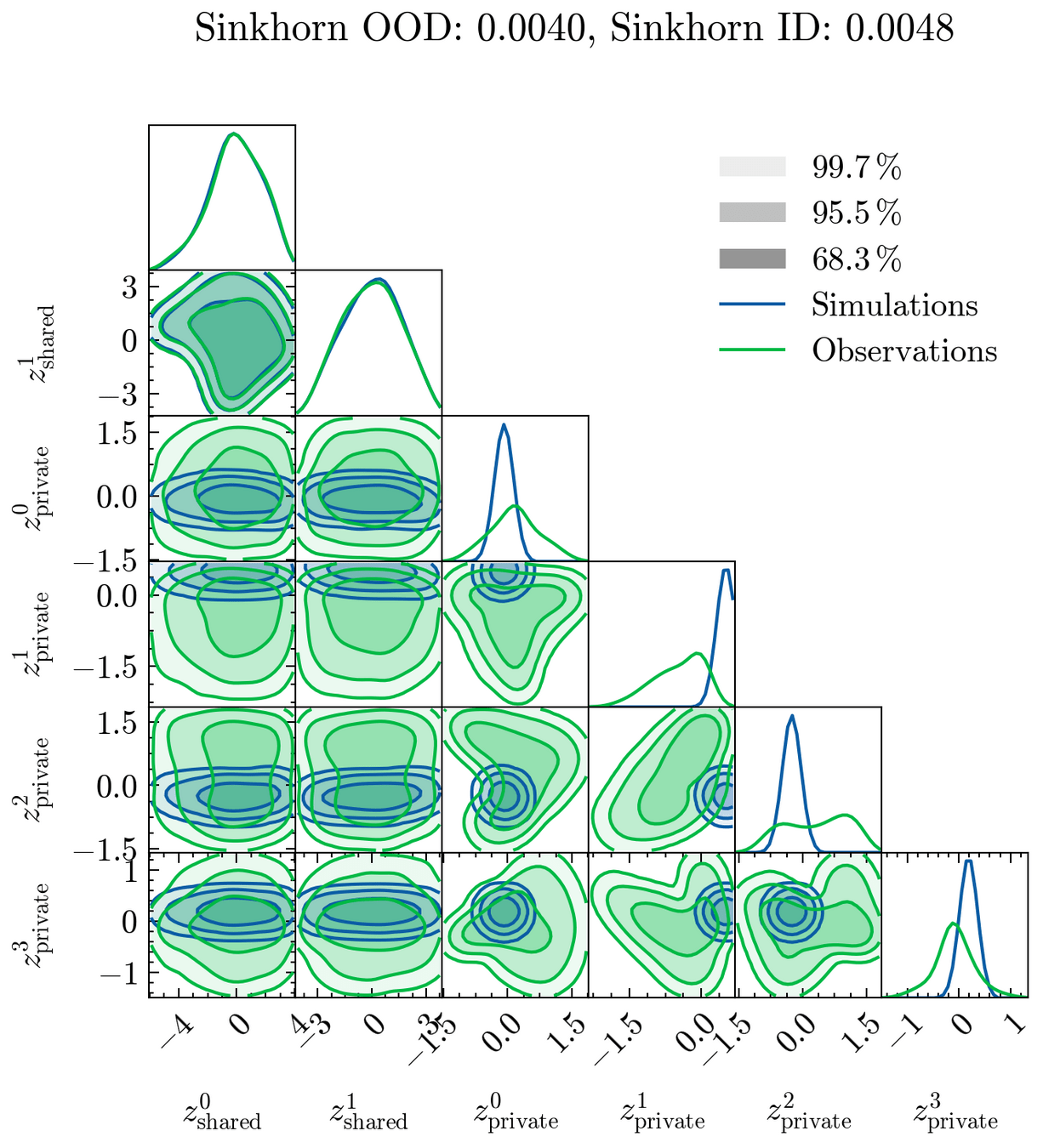
z^\mathcal{O}_p
z^\mathcal{O}_s
z^\mathcal{S}_s
z^\mathcal{S}_p
Alignment Loss
\mathcal{L} = \sum_{\mathcal{D} \in (\mathcal{S}, \mathcal{O})} p(x^\mathcal{D}|z^\mathcal{D}_s, z^\mathcal{D}_p) + \lambda d(z^\mathcal{O}_s,z^\mathcal{S}_s)
Reconstruction
Statistical Alignment
50\%
(OT / Adversarial)
Encoder
Obs
Encoder
Sims
Private Domain Information
Shared Information
\hat{x}^\mathcal{O}
\hat{x}^\mathcal{S}
Observed Reconstructed
Simulated Reconstructed
Shared Decoder
Shared Decoder
Carolina Cuesta-Lazaro Flatiron/IAS
A Toy Model Example
Idealized Simulations
Observations
+ Scale Dependent Noise
+ Bump
x^\mathcal{O}
x^\mathcal{S}
Carolina Cuesta-Lazaro Flatiron/IAS
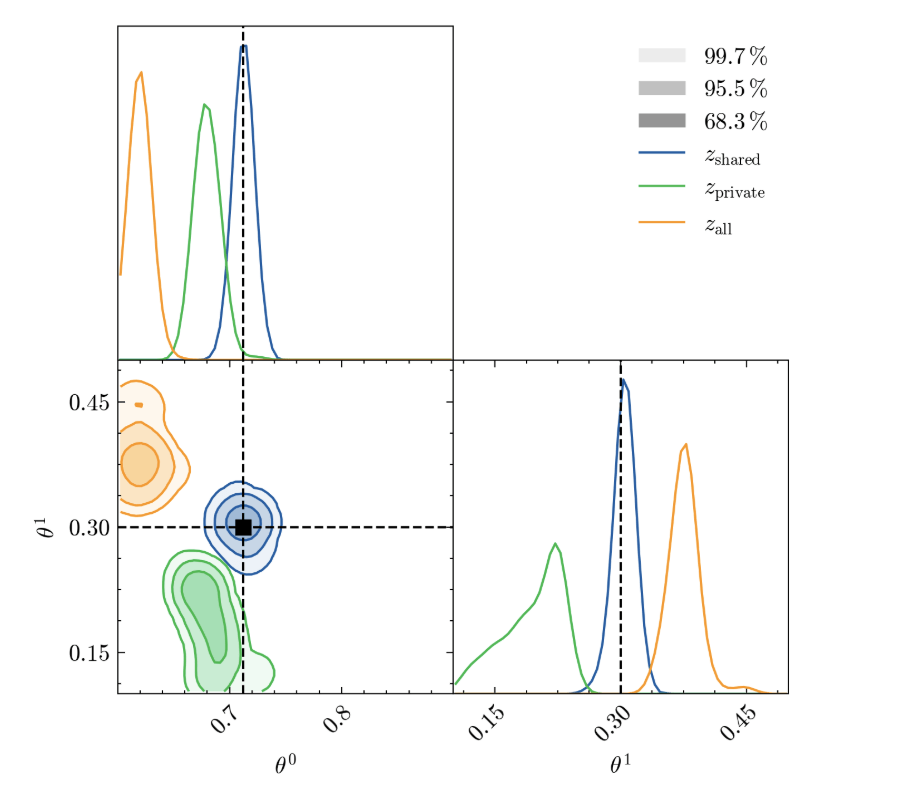
Amplitude
Tilt
Tilt
p(\theta|z^\mathcal{O}_s)
p(\theta|z^\mathcal{O}_p)
p(\theta|z^\mathcal{O}_p,z^\mathcal{O}_s)
p(\theta|z^\mathcal{O}_p)
Robust SBI from Shared
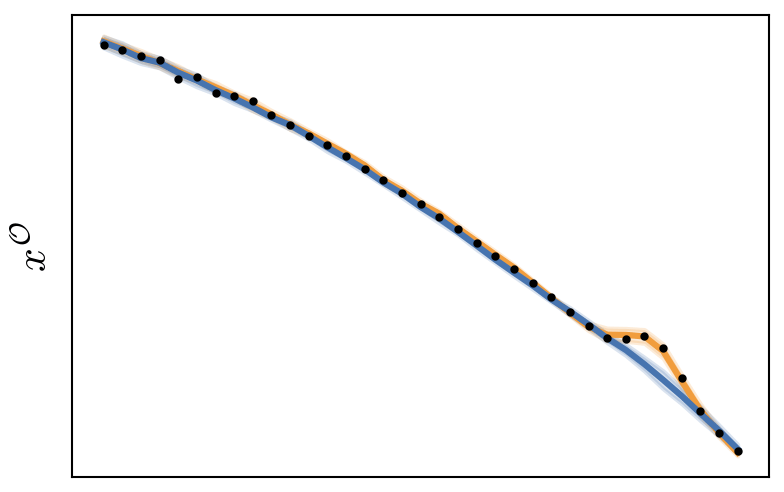
p(x^\mathcal{O}|z^\mathcal{O}_p,z^\mathcal{O}_s)
p(x^\mathcal{O}|z^\mathcal{O}_s)
Visualizing Information Split
Carolina Cuesta-Lazaro Flatiron/IAS
Princeton-BahcallLunch-2025
By carol cuesta
