MLizing cosmology
florpi
The What? How? And Why?
And really, Why?
https://florpi.github.io/
IAIFI Fellow
Carol Cuesta-Lazaro
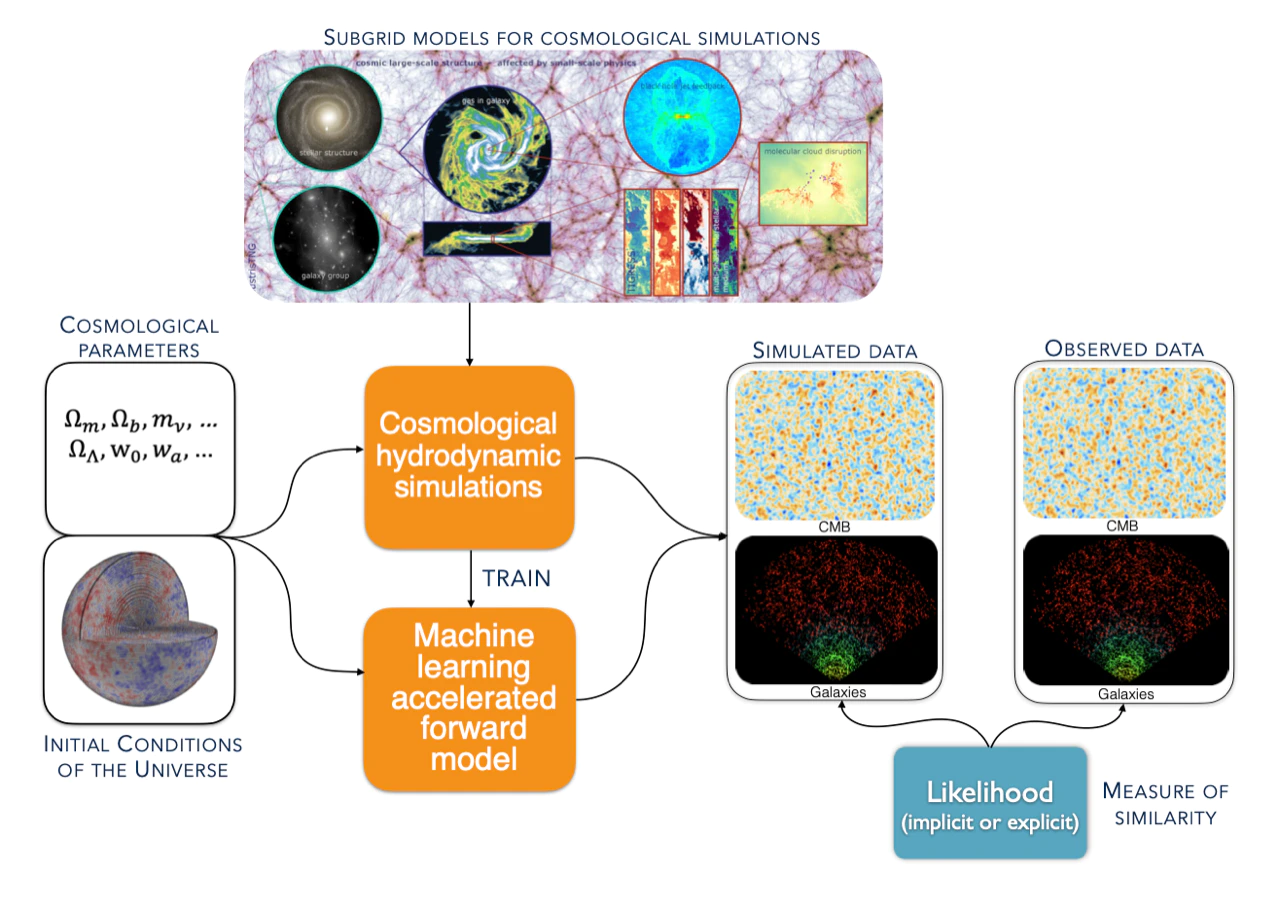
Initial Conditions of the Universe
Laws of gravity
3-D distribution of galaxies
Which are the ICs of OUR Universe?
Primordial non-Gaussianity?
Probe Inflation
Galaxy formation
3-D distribution of dark matter
Is GR modified on large scales?
How do galaxies form?
Neutrino mass hierarchy?
The Why: The limits of analytical models
But... Access to tones of data!
simulated data
Complex non-Gaussian distributions
Non-linear forward models
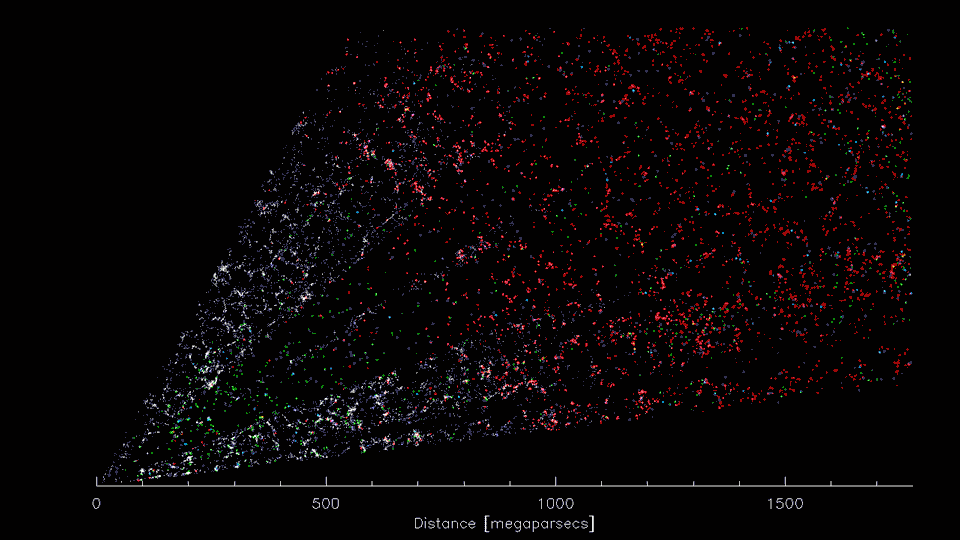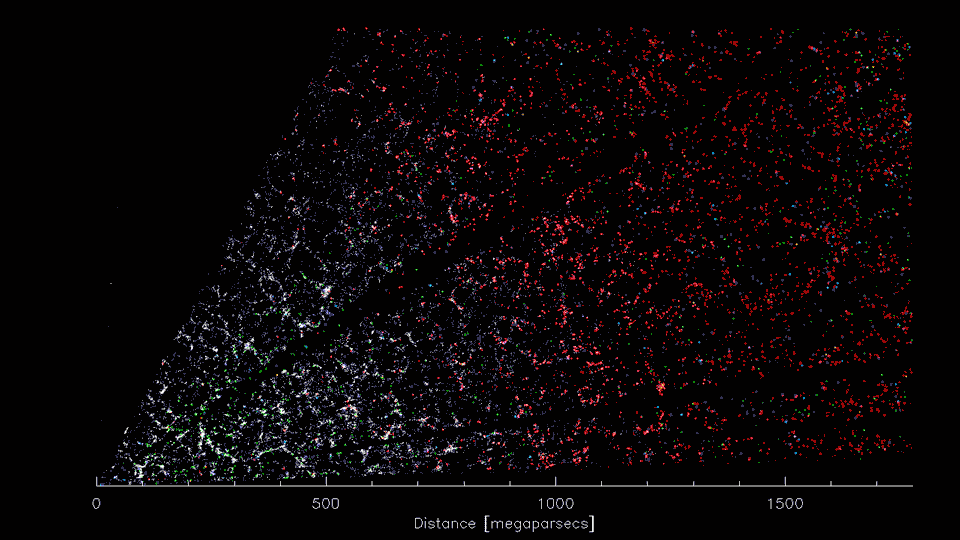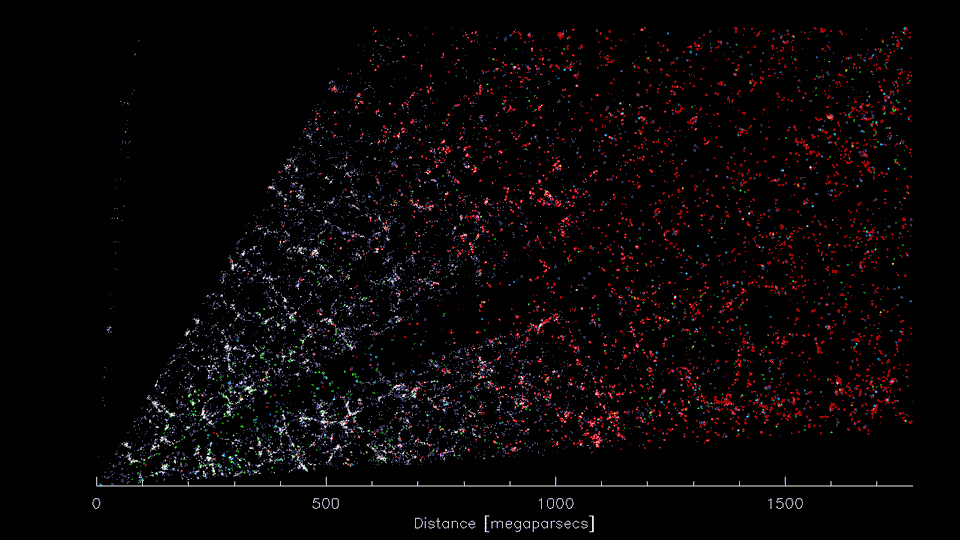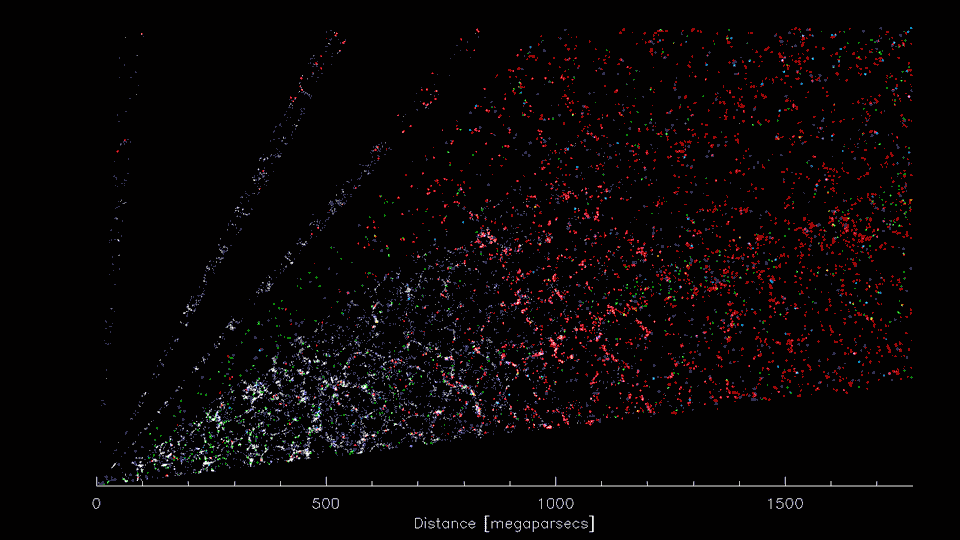
(Image Credit: D. Schlegel/Berkeley Lab using data from DESI)
A 2D animation of a folk music band composed of anthropomorphic autumn leaves, each playing traditional bluegrass instruments, amidst a rustic forest setting dappled with the soft light of a harvest moon
ML has solved high-dimensional inference
#1 Field-level likelihoods for galaxy surveys
Siddharth Mishra-Sharma
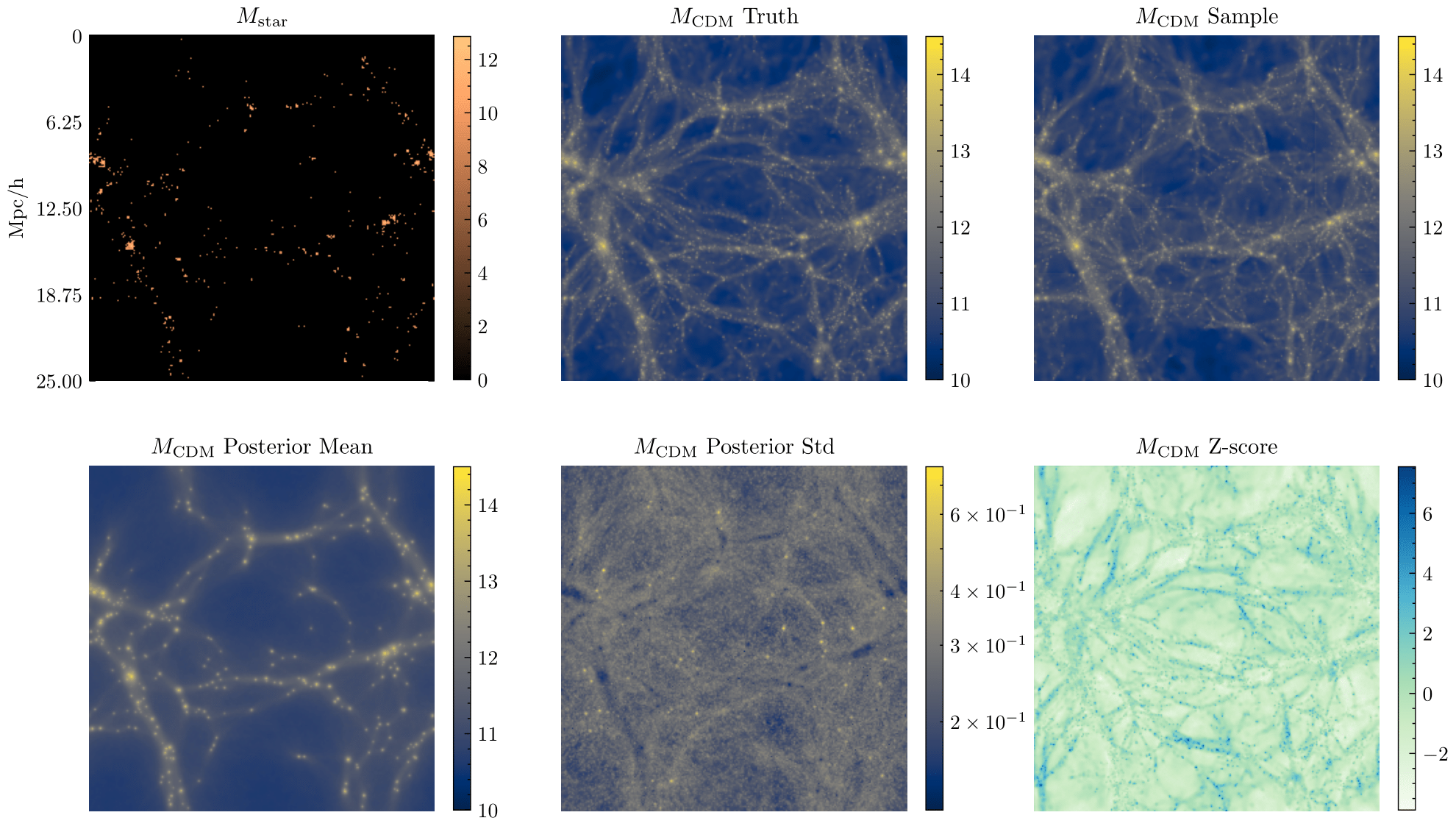
#2 Probabilistic reconstruction of the cosmic web
Core Park
Nayantara Mudur
Victoria Ono
Yueying Ni
#3 Faster, invertible and more accurate simulators
Sarah Jeffreson
Chirag Modi
Generative Models 101
p(x)
x_1
x_2
Samples
Parametric PDF
Maximize the likelihood of the training samples
\hat \theta = \argmax \left[ \log p_\theta (x_\mathrm{train}) \right]
p_\theta(x)
x
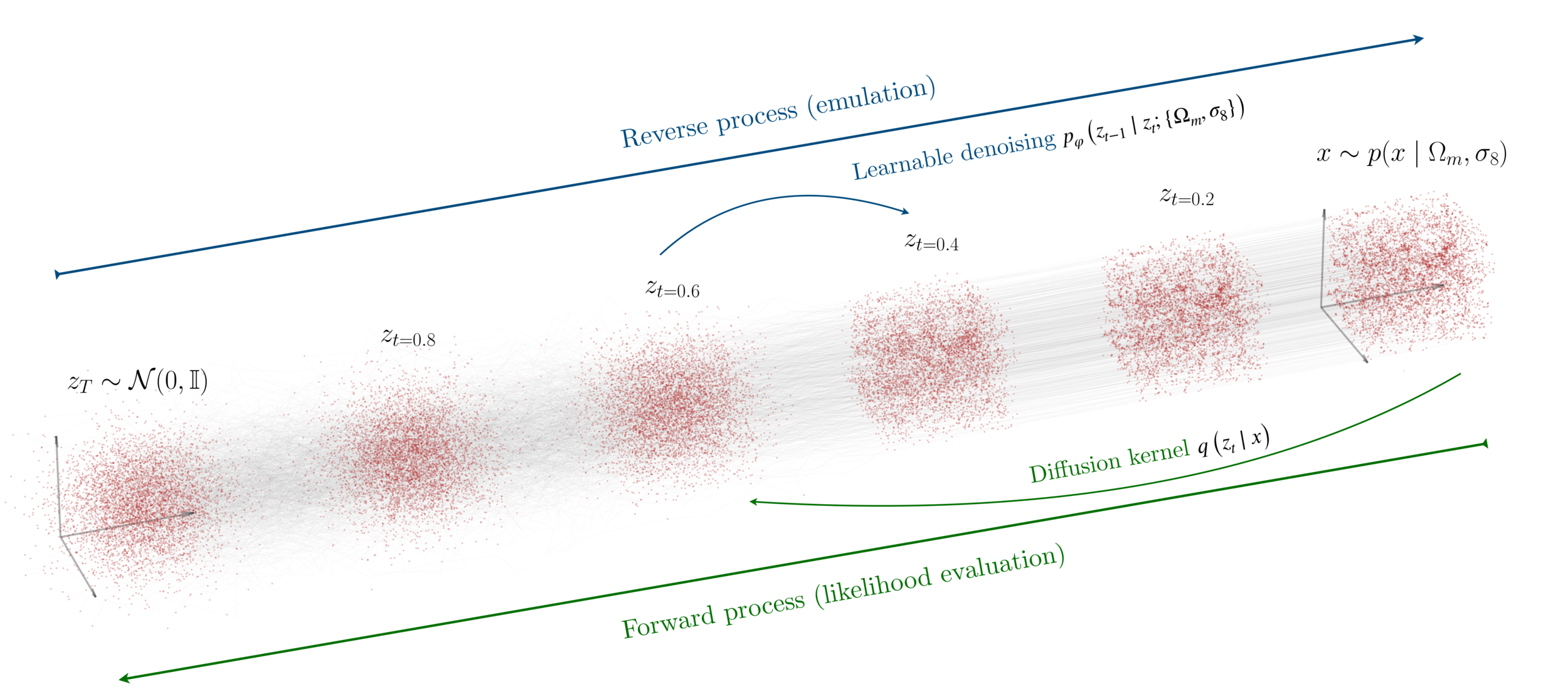
Reverse diffusion: Denoise previous step
Forward diffusion: Add Gaussian noise (fixed)
A person half Yoda half Gandalf
q_\theta(z_0|z_1)
p(z_1|z_0)
Diffusion generative models
p(z_0)
p(z_T)
p(z_2)
p(z_1)
p(z_2|z_1)
p(z_T|z_2)
q_\theta(z_1|z_2)
q_\theta(z_2|z_T)
s_\theta(x,t) = \nabla_x \log p_t(x)
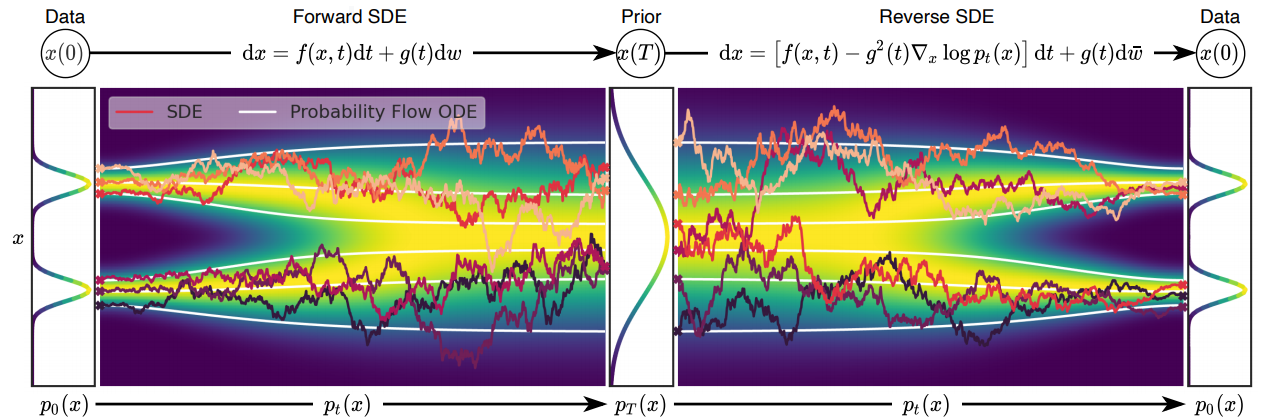
Score
#1 Modelling galaxy surveys
"A point cloud approach to generative modeling for galaxy surveys at the field level"
arXiv:2311.17141
Carolina Cuesta-Lazaro and Siddharth Mishra-Sharma
2PCF
Mean pairwise
velocity
kNN
Emulating cosmic variance
2PCF
kNN
Diffusion models approximate the likelihood
\log p(z_0) = \log \int p(z_{0:T}) dz_{1:T} \approx
\approx \sum_{i=1}^T \mathbb{E}_{q(z_{i}|z_0)} D_{KL} \left[p(z_i | z_{i-1}, z_0) || q_\theta(z_{i-1} | z_{i}) \right]
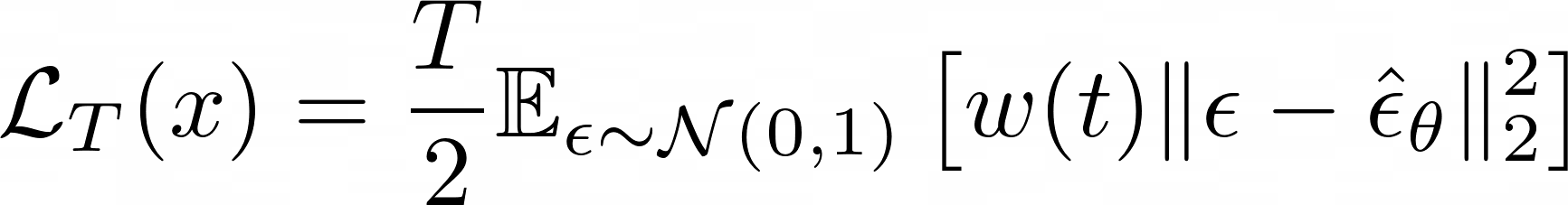
arxiv:2107.00630
arxiv:2208.11970
Maximum Likelihood = Denoising
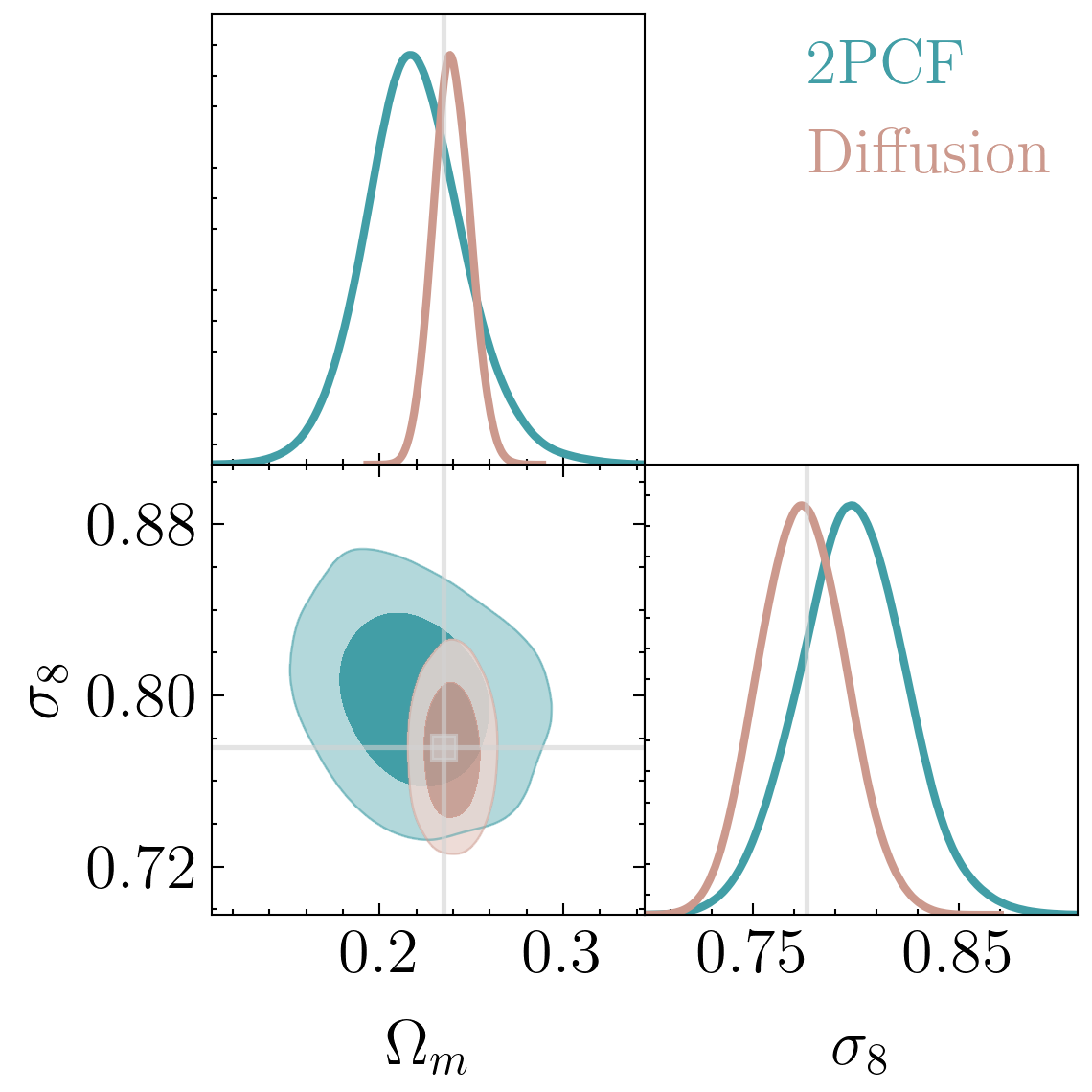
Tight constraints with only 5000 positions!
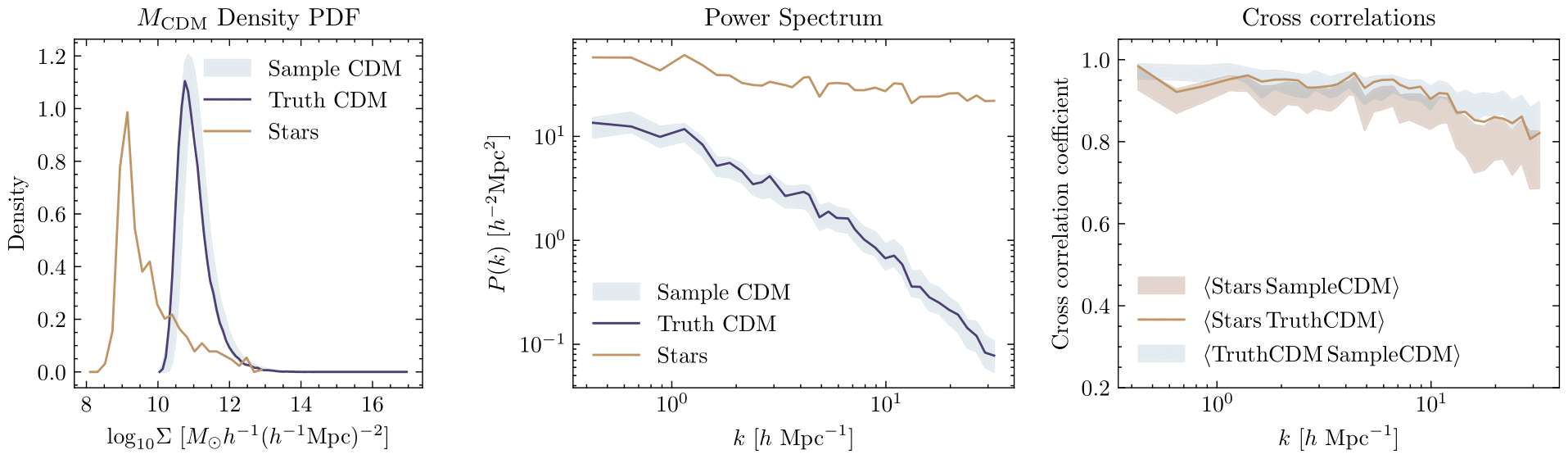
"Probabilistic Reconstruction of Dark Matter fields from galaxies using diffusion models"
arXiv:2311.08558
Core Francisco Park, Victoria Ono, Nayantara Mudur, Yueying Ni, Carolina Cuesta-Lazaro p_\phi(x_\mathrm{DM}|x_\mathrm{Stars})
#2 Solving inverse problems:
Probabilistic reconstruction of the cosmic web
1 to Many:
25 \, h^{-1}\mathrm{Mpc}
#3 AI Powered simulators
Fast and differentiable N-body sims
Inverting dynamics
More accurate hydro sims: Resolving star formation rates
z=120
z=0.2
~10-100 pc
Molecular clouds
where stars form
Hydro sims:
A matrioska of scales
~10-50 kpc
Galaxies
where clouds form
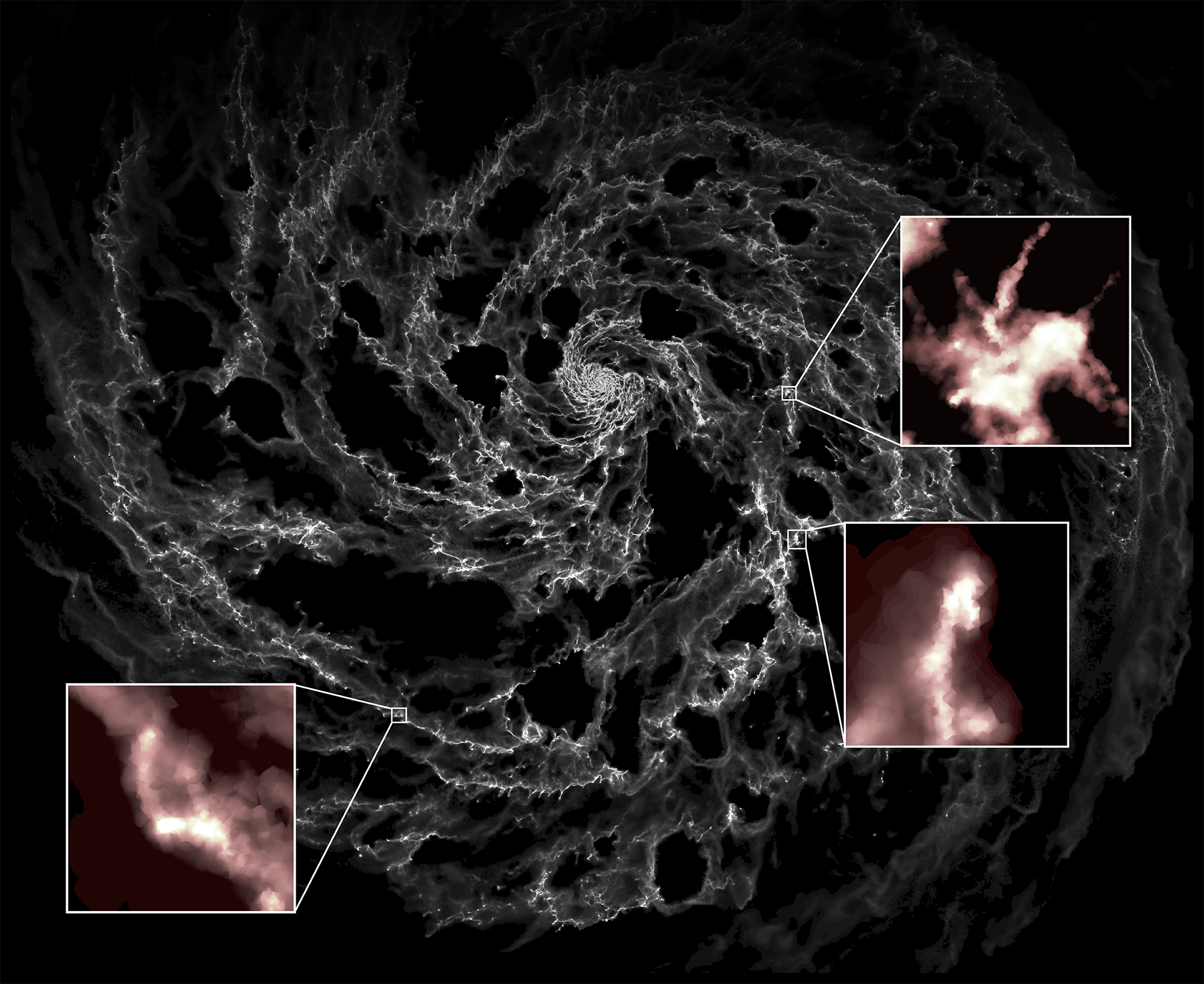
TNG50 ~50 Mpc
Cosmic web
(where galaxies form)
MXXL ~ 4 Gpc
Adapted from: "Learning the learning the Universe" by Jake BennetCurrent subgrid models of the ISM
High Res Sim
Springel and Hernquist 03
Learning subgrid models from high resolution isolated galaxies
Gas Surface Density
SFR Surface Density
Hybrid simulators
Nbody
Slow
Non-differentiable
Particle mesh
Accurate
Fast
Differentiable
Missing small scales
Nbodyify
Fast
Differentiable
Accurate
"Nbodyify: adaptive mesh corrections for PM simulations"
Carolina Cuesta-Lazaro and Chirag Modi (in prep)\frac{\mathrm{d} \mathbf{x}}{\mathrm{d} a } = \frac{1}{a^3 E(a)}\mathbf{v}
\frac{\mathrm{d} \mathbf{v}}{\mathrm{d} a } = \frac{1}{a^2 E(a)}\mathbf{F}(\mathbf{x},a)
\mathbf{F}_\theta(\mathbf{x},a) = \frac{3 \Omega_m}{2} \nabla \left[\phi^\mathrm{PM}(\mathbf{x}) + \phi^\mathrm{corr}_\theta(\mathbf{x}, a, \phi^\mathrm{PM}, \delta^\mathrm{PM}) \right]
\mathbf{F}(\mathbf{x},a) = \frac{3 \Omega_m}{2} \nabla \phi^\mathrm{PM}(\mathbf{x})
Gravitational evolution ODE
Particle-mesh
Hybrid Simulator
#2 Probabilistic reconstruction of the cosmic web
#1 Field-level likelihoods for galaxy surveys
#3 Faster, invertible and more accurate simulators
cuestalz@mit.edu
MLizing cosmology
By carol cuesta
