Simulation-based inference
Boomers Quantified Uncertainty. We Simulate It
[Video Credit: N-body simulation Francisco Villaescusa-Navarro]
IAIFI Fellow
Carolina Cuesta-Lazaro
IAIFI Summer School
Why should I care?
Decision making
Decision making in science
Carolina Cuesta-Lazaro IAIFI/MIT - Simulation-Based Inference
Is the current Standard Model ruled out by data?
Mass density
Vacuum Energy Density
0
CMB
Supernovae
\Omega_m
\Omega_\Lambda
Observation
Ground truth
Prediction
Uncertainty
Is it safe to drive there?
Carolina Cuesta-Lazaro IAIFI/MIT - Simulation-Based Inference
Better data needs better models
p(\mathrm{theory} | \mathrm{data})
Interpretable Simulators
Carolina Cuesta-Lazaro IAIFI/MIT - Simulation-Based Inference
\mathrm{data}
\mathrm{theory}
Uncertainties are everywhere
x^i_1
x^i_2
Noise in features
+ correlations
Noise in finite data realization
\{x^1, x^2,...,x^N \}
\theta
p(\theta|x)
\phi
Uncertain parameters
Limited model architecture
Imperfect optimization
N \gg 1
Carolina Cuesta-Lazaro IAIFI/MIT - Simulation-Based Inference
Ensembling / Bayesian NNs
\theta
Forward Model
Observable
x
\color{darkgray}{\Omega_m}, \color{darkgreen}{w_0, w_a},\color{purple}{f_\mathrm{NL}}\, ...
Dark matter
Dark energy
Inflation
Predict
Infer
Parameters
Carolina Cuesta-Lazaro IAIFI/MIT - Simulation-Based Inference
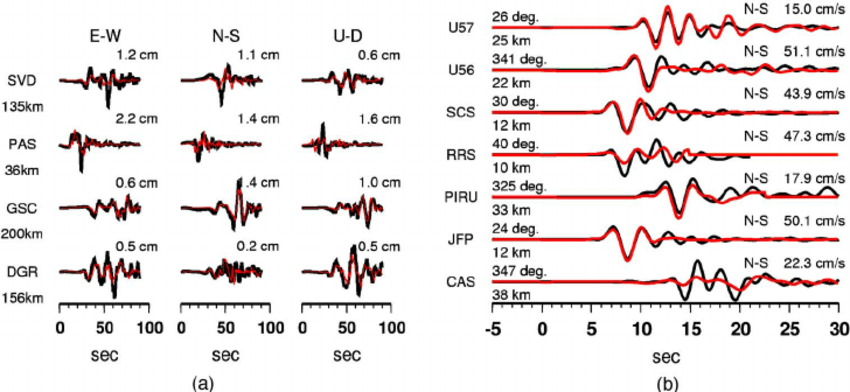
Inverse mapping
\color{darkgray}{\sigma}, \color{darkgreen}{v}, ...
Fault line stress
Plate velocity
q_\phi(\theta|x) \approx
Variational
Posterior
\color{white}{p(\theta|x)} \color{black}{=} \frac{\color{white}{p(x|\theta)} \color{white}{p(\theta)}}{\color{white}{p(x)}}
Likelihood
Posterior
Prior
Evidence
p(\theta|x)
p(x|\theta)
p(\theta)
p(x)
Markov Chain Monte Carlo MCMC
Hamiltonian Monte Carlo HMC
Variational Inference VI
Carolina Cuesta-Lazaro IAIFI/MIT - Simulation-Based Inference
p(x) = \int p(x|\theta) p(\theta) d\theta
If can evaluate posterior (up to normalization), but not sample
Intractable
Unknown likelihoods
Amortized inference
Scaling high-dimensional
Marginalization nuisance
Carolina Cuesta-Lazaro IAIFI/MIT - Simulation-Based Inference
Image Credit: Chi Feng mcmc demo
Carolina Cuesta-Lazaro IAIFI/MIT - Simulation-Based Inference
["Polychord: nested sampling for cosmology" Handley et al]
["Fluctuation without dissipation: Microcanonical Langevin Monte Carlo" Robnik and Seljak]
The price of sampling
Higher Effective Sample Size (ESS) = less correlated samples
Number of Simulator Calls
Known likelihood
Differentiable simulators
The simulator samples the likelihood
Carolina Cuesta-Lazaro IAIFI/MIT - Simulation-Based Inference
x_\mathrm{final}, y_\mathrm{final} \sim \mathrm{Simulator}(f, \theta) = p(x_\mathrm{final}, y_\mathrm{final} \mid f, \theta)
p(x_\mathrm{final}, y_\mathrm{final}|f, \theta) = \int dz p(x_\mathrm{final}, y_\mathrm{final},z|f, \theta)
z: All possible trajectories
Maximize the likelihood of the training samples
\hat \phi = \argmax \left[ \log p_\phi (x_\mathrm{train}|\theta_\mathrm{train}) \right]
Model
p_\phi(x)
Training Samples
x_\mathrm{train}
Carolina Cuesta-Lazaro IAIFI/MIT - Simulation-Based Inference
Neural Likelihood Estimation NLE
x_\mathrm{final}, y_\mathrm{final} \sim p(x_\mathrm{final}, y_\mathrm{final} \mid f, \theta) p(f, \theta)
NLE
No implicit prior
Not amortized
Goodness-of-fit
Scaling with dimensionality of x
p(x|\theta)
Implicit marginalization
\mathcal{L}(\phi) \approx -\frac{1}{N} \sum_{i=1}^N \log q_\phi(x_i \mid \theta_i )
Neural Posterior Estimation NPE
D_{\text{KL}}(p(\theta \mid x) \parallel q_\phi(\theta \mid x)) = \mathbb{E}_{\theta \sim p(\theta \mid x)} \log \frac{p(\theta \mid x)}{q_\phi(\theta \mid x)}
Loss Approximate variational posterior, q, to true posterior, p
q_\phi(\theta \mid x)
p(\theta \mid x)
Image Credit: "Bayesian inference; How we are able to chase the Posterior" Ritchie Vink
Carolina Cuesta-Lazaro IAIFI/MIT - Simulation-Based Inference
KL Divergence
\mathcal{L}(\phi) = -\mathbb{E}_{\theta \sim p(\theta \mid x)} \left[ \log q_\phi(\theta \mid x) \right]
\mathcal{L}(\phi) = -\int p(\theta \mid x) \log q_\phi(\theta \mid x) \, d\theta
= -\int \frac{p(x \mid \theta) p(\theta)}{p(x)} \log q_\phi(\theta \mid x) \, d\theta.
\propto -\int p(x \mid \theta) p(\theta) \log q_\phi(\theta \mid x) \, d\theta.
D_{\text{KL}}(p(\theta \mid x) \parallel q_\phi(\theta \mid x)) = \mathbb{E}_{\theta \sim p(\theta \mid x)} \log \frac{p(\theta \mid x)}{q_\phi(\theta \mid x)}
Need samples from true posterior
Run simulator
Carolina Cuesta-Lazaro IAIFI/MIT - Simulation-Based Inference
p(x,\theta)
\phi^* = \argmin_{\phi}
Minimize KL
\mathbb{E}_{p(\theta, x)}
\mathcal{L}(\phi) \approx -\frac{1}{N} \sum_{i=1}^N \log q_\phi(\theta_i \mid x_i)
\mathcal{L}(\phi) = -\mathbb{E}_{(\theta, x) \sim p(\theta, x)} \left[ \log q_\phi(\theta \mid x) \right]
(\theta_i, x_i) \sim p(\theta, x)
Amortized Inference!
Carolina Cuesta-Lazaro IAIFI/MIT - Simulation-Based Inference
Run simulator
Neural Posterior Estimation NPE
Neural Compression
x
s = F_\eta(x)
High-Dimensional
Low-Dimensional
Carolina Cuesta-Lazaro IAIFI/MIT - Simulation-Based Inference
p(\theta|x) = p(\theta|s)
s is sufficient iif
Neural Compression: MI
I(s(x), \theta)
Maximise
Mutual Information
I(\theta, s(x)) = D_{\text{KL}}(p(\theta, s(x)) \parallel p(\theta)p(s(x)))
\theta, s(x) \, \, \mathrm{independent} \rightarrow p(\theta, s(x)) = p(\theta)p(s(x))
s(x)
\theta
I(s(x), \theta)
\theta, s(x)
Carolina Cuesta-Lazaro IAIFI/MIT - Simulation-Based Inference
I(\theta, s(x)) = \mathbb{E}_{p(\theta, s(x))} \left[ \log \frac{p(\theta, s(x))}{p(\theta)p(s(x))} \right]
= \mathbb{E}_{p(\theta, s(x))} \left[ \log \frac{p(\theta \mid s(x))p(s(x))}{p(\theta) p(s(x))} \right]
p(\theta, s(x)) = p(\theta \mid s(x)) p(s(x))
Need true posterior!
I(\theta, s(x)) \approx \mathbb{E}_{p(\theta, s(x))} \left[ \log \frac{q_\phi(\theta \mid s(x))}{p(\theta)} \right]
\mathcal{L}(\phi, \eta) \approx -\frac{1}{N} \sum_{i=1}^N \log q_\phi(\theta_i \mid s_\eta(x_i))
Carolina Cuesta-Lazaro IAIFI/MIT - Simulation-Based Inference
NLE
No implicit prior
Not amortized
Goodness-of-fit
Scaling with dimensionality of x
p(x|\theta)
NPE
p(\theta|x)
Amortized
Scales well to high dimensional x
Goodness-of-fit
Fixed prior
Implicit marginalization
\mathcal{L}(\phi) \approx -\frac{1}{N} \sum_{i=1}^N \log q_\phi(\theta_i \mid x_i)
\mathcal{L}(\phi) \approx -\frac{1}{N} \sum_{i=1}^N \log q_\phi(x_i \mid \theta_i )
Implicit marginalization
Do we actually need Density Estimation?
Just use binary classifiers!
x, \theta \sim p(x,\theta)
x, \theta \sim p(x)p(\theta)
y = 1
y = 0
\theta
x
Binary cross-entropy
Sample from simulator
Mix-up
Carolina Cuesta-Lazaro IAIFI/MIT - Simulation-Based Inference
Likelihood-to-evidence ratio
r(x,\theta) = \frac{p(x\mid \theta)}{p(x)}
Likelihood-to-evidence ratio
p(x,\theta|y) = p(x,\theta) \, \, \mathrm{if} \, \, y=1
p(x,\theta|y) = p(x)p(\theta) \, \, \mathrm{if} \, \, y=0
p(y=1 \mid x,\theta) = \frac{p(x,\theta|y=1)p(y)}{p(x,\theta)}
\left(p(x,\theta \mid y=0) + p(x,\theta \mid y=1) \right)p(y)
p(y=1 \mid x,\theta) = \frac{p(x,\theta)}{p(x)p(\theta) + p(x,\theta)}
= \frac{p(x,\theta)}{p(x)p(\theta)}
= \frac{r(x,\theta)}{r(x,\theta) + 1}
Carolina Cuesta-Lazaro IAIFI/MIT - Simulation-Based Inference
\frac{p(y=1 \mid x,\theta)}{p(y=0 \mid x,\theta)} = \frac{p(y=1 \mid x,\theta)}{1 - p(y=0 \mid x,\theta)}
p(y=1 \mid x,\theta) = \sigma(s(x,\theta)) = \frac{1}{1 + \exp^{-s(x,\theta)}}
\frac{p(y=1 \mid x,\theta)}{p(y=0 \mid x,\theta)} = \exp^{s(x,\theta)}
s(x,\theta) = \log \left( \frac{p(y=1 \mid x,\theta)}{p(y=0 \mid x,\theta)} \right) = \log(r(x,\theta))
Carolina Cuesta-Lazaro IAIFI/MIT - Simulation-Based Inference
Classifier logits
Classifier logits
=
log(Likelihood-to-evidence ratio)
NLE
No implicit prior
Not amortized
Goodness-of-fit
Scaling with dimensionality of x
p(x|\theta)
NPE
p(\theta|x)
NRE
\frac{p(x|\theta)}{p(x)}
Amortized
Scales well to high dimensional x
Goodness-of-fit
Fixed prior
Implicit marginalization
\mathcal{L}(\phi) \approx -\frac{1}{N} \sum_{i=1}^N \log q_\phi(\theta_i \mid x_i)
\mathcal{L}(\phi) \approx -\frac{1}{N} \sum_{i=1}^N \log q_\phi(x_i \mid \theta_i )
No need variational distribution
No implicit prior
Implicit marginalization
Approximately normalised
\begin{split}
L &= - \frac{1}{N} \sum_{i=1}^N \left[ y_i \log(p_i) \right. \\
&\left. + (1 - y_i) \log(1 - p_i) \right]
\end{split}
Not amortized
Implicit marginalization
Density Estimation 101
Maximize the likelihood of the training samples
\hat \phi = \argmax \left[ \log p_\phi (x_\mathrm{train}) \right]
x_1
x_2
Model
p_\phi(x)
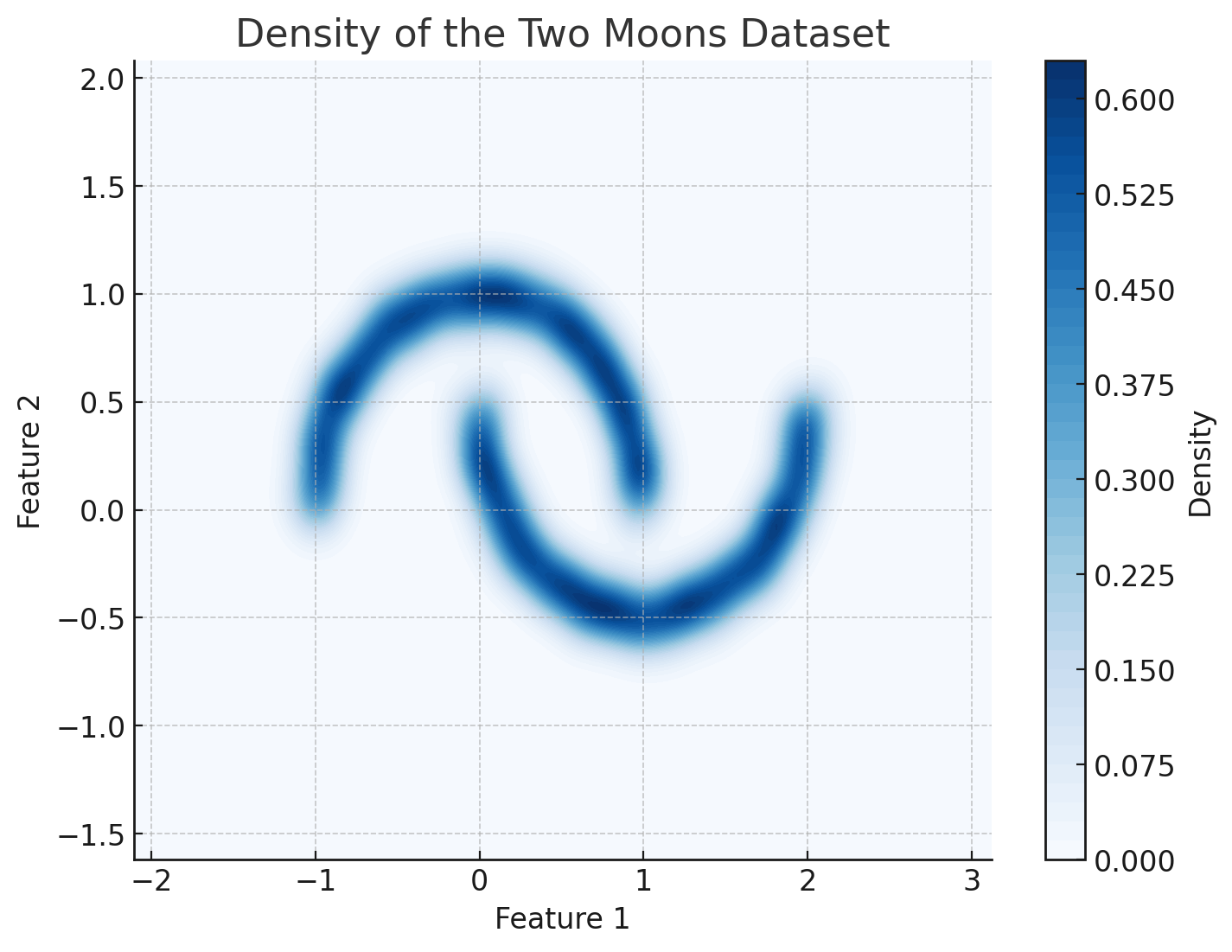
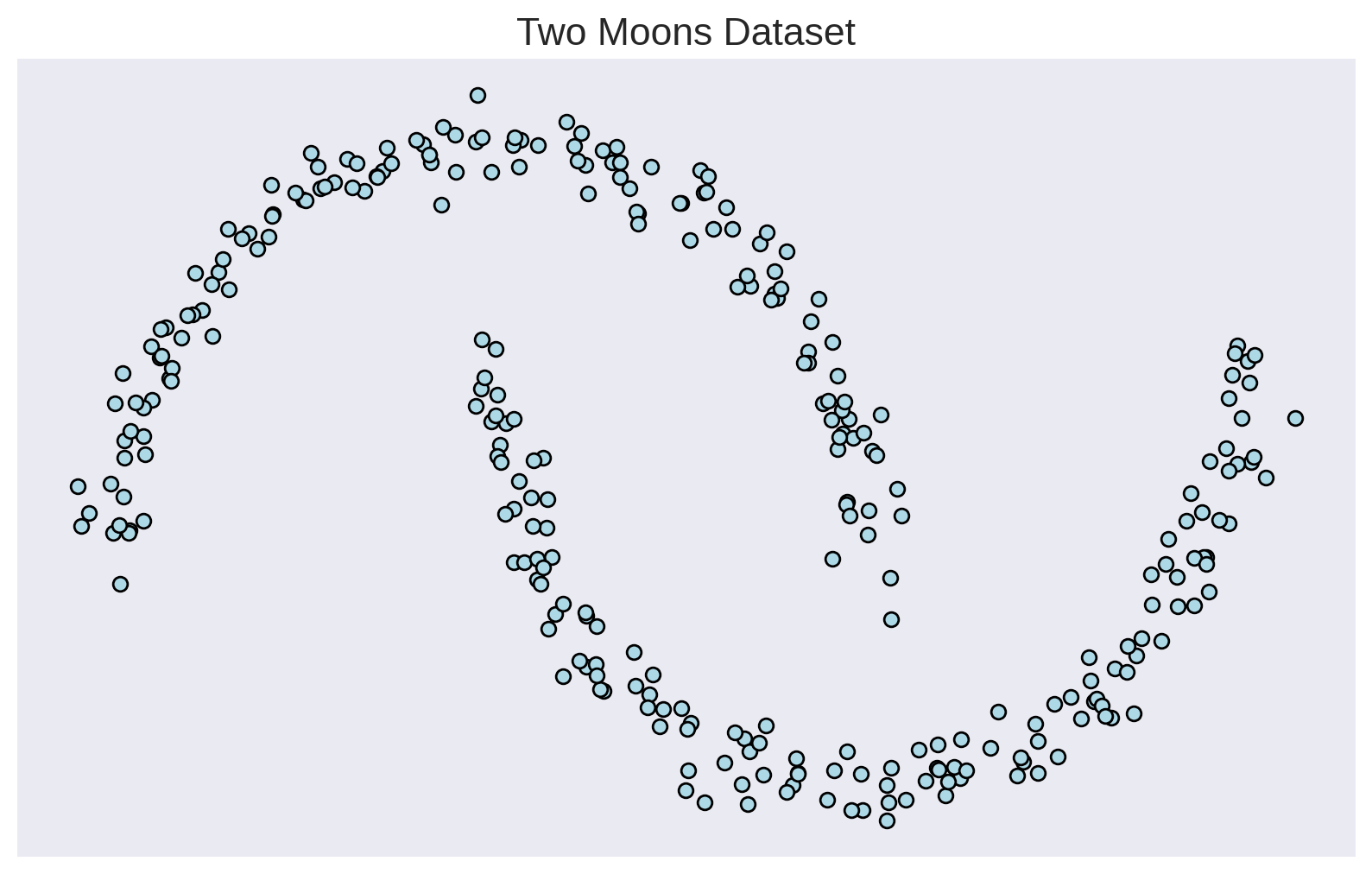
Training Samples
x_\mathrm{train}
Carolina Cuesta-Lazaro IAIFI/MIT - Simulation-Based Inference
x_1
x_2
Trained Model
p_\phi(x)
Evaluate probabilities
Low Probability
High Probability
Generate Novel Samples
Simulator
Simulator
Carolina Cuesta-Lazaro IAIFI/MIT - Simulation-Based Inference
Normalizing flows
[Image Credit: "Understanding Deep Learning" Simon J.D. Prince]
z \sim p(z)
x \sim p(x)
x = f(z)
p(x) = p(z = f^{-1}(x)) \left| \det J_{f^{-1}}(x) \right|
Carolina Cuesta-Lazaro IAIFI/MIT - Simulation-Based Inference
Bijective
Sample
Evaluate probabilities
Probability mass conserved locally
z_0 \sim p(z)
z_k = f_k(z_{k-1})
\log p(x) = \log p(z_0) - \sum_{k=1}^{K} \log \left| \det J_{f_k} (z_{k-1}) \right|
Image Credit: "Understanding Deep Learning" Simon J.D. Prince
Carolina Cuesta-Lazaro IAIFI/MIT - Simulation-Based Inference
Carolina Cuesta-Lazaro IAIFI/MIT - Simulation-Based Inference
Masked Autoregressive Flows
p(x) = \prod_i{p(x_i \,|\, x_{1:i-1})}
p(x_i \,|\, x_{1:i-1}) = \mathcal{N}(x_i \,|\,\mu_i, (\exp\alpha_i)^2)
\mu_i, \alpha_i = f_{\phi_i}(x_{1:i-1})
Neural Network
x_i = z_i \exp(\alpha_i) + \mu_i
z_i = (x_i - \mu_i) \exp(-\alpha_i)
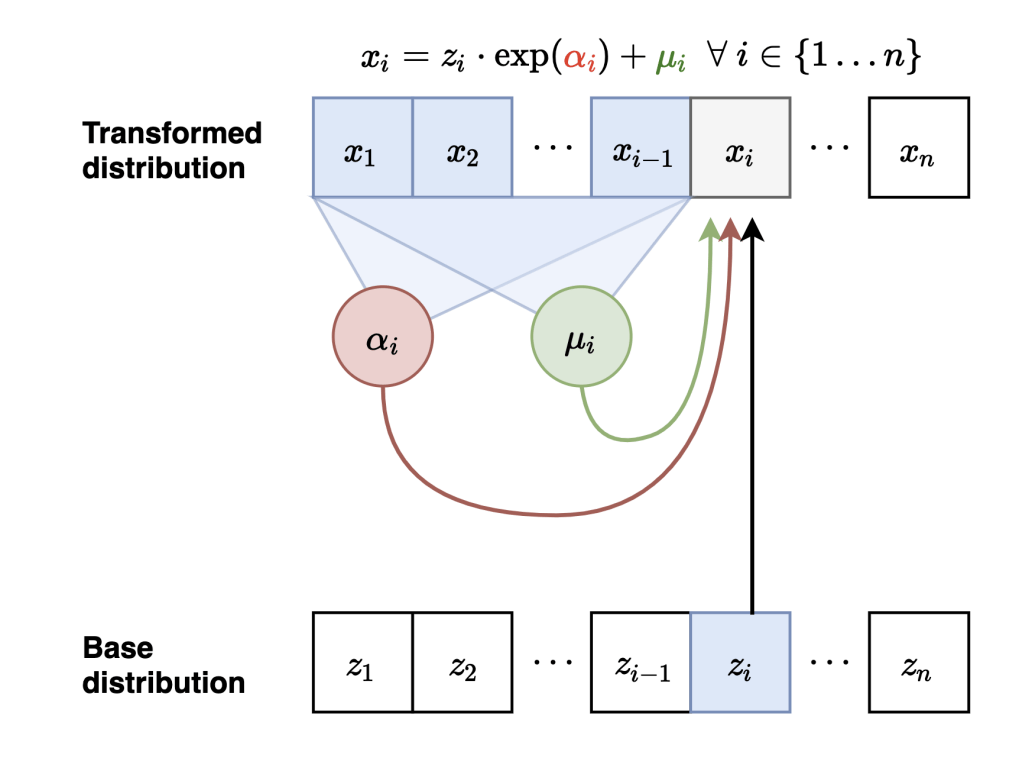
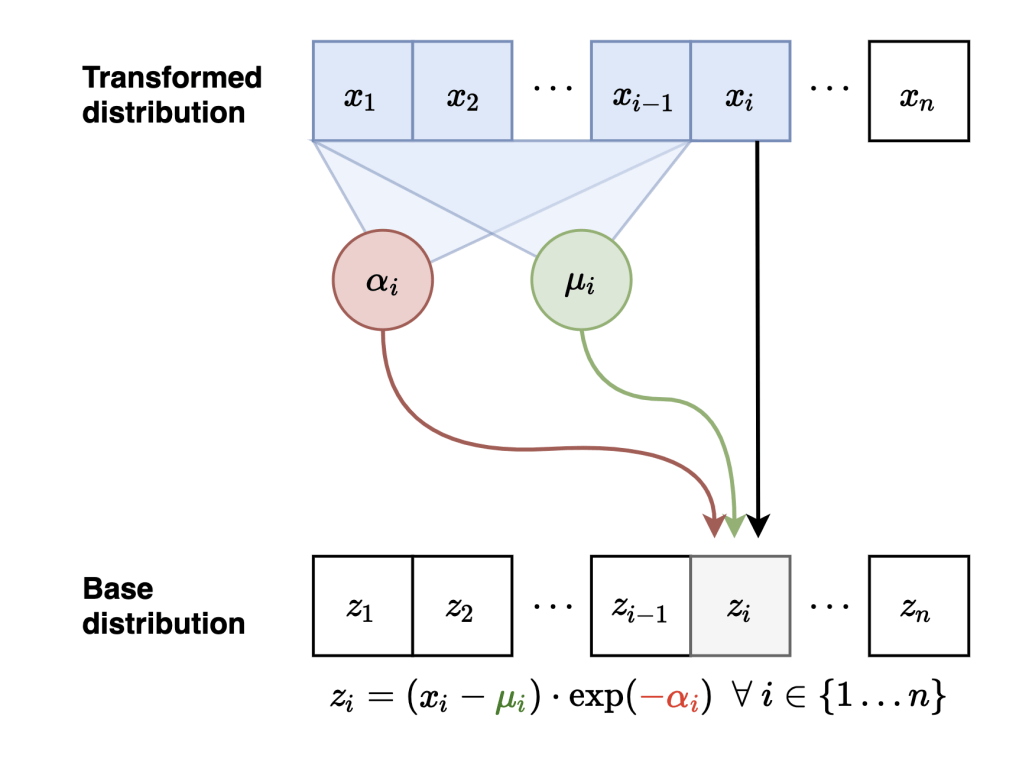
Sample
Evaluate probabilities
\frac{dz_t}{dt} = u^\phi_t(z_t)
x = z_0 + \int_0^1 u^\phi_t(z_t) dt
Continuity equation
\frac{d p(z_t)}{dt} = - \nabla \left( u^\phi_t(z_t) p(z_t) \right)
[Image Credit: "Understanding Deep Learning" Simon J.D. Prince]
Carolina Cuesta-Lazaro IAIFI/MIT - Simulation-Based Inference
Continuous time Normalizing flows
\log p(x) = \log p(z_0) + \int_0^1 \mathrm{Tr} J_{u^\phi_t} (z_t) dt
Need to solve this expensive integral at each step during training to maximise likelihood!
Very slow -> Difficult to scale to high dims
Can we avoid it?
\frac{d p(z_t)}{dt} = - \nabla \left( u^\phi_t(z_t) p(z_t) \right)
Restricted trajectories: flow matching / diffusion
Carolina Cuesta-Lazaro IAIFI/MIT - Simulation-Based Inference
Flow matching
\mathcal{L} = \mathbb{E}_{t \sim \mathcal{U}[0, 1]} \mathbb{E}_{x_t \sim p_t}\left[\|
u_t^\phi(x_t) - u_t(x_t) \|^2 \right]
Regress the velocity field directly!
[Image Credit: "An Introduction to flow matchig" Tor Fjelde et al]
Carolina Cuesta-Lazaro IAIFI/MIT - Simulation-Based Inference
["Flow Matching for Generative Modeling" Lipman et al]
["Stochastic Interpolants: A Unifying framework for Flows and Diffusions" Albergo et al]
Conditional Flow matching
x_t = (1-t) x_0 + t x_1
\mathcal{L}_\mathrm{conditional} = \mathbb{E}_{t,x_0,x_1}\left[\|
u_t^\phi(x_t) - u_t(x_0,x_1) \|^2 \right]
Assume a conditional vector field (known at training time)
The loss that we can compute
The gradients of the losses are the same!
\nabla_\phi \mathcal{L}_\mathrm{conditional} = \nabla_\phi \mathcal{L}
x_0
x_1
Carolina Cuesta-Lazaro IAIFI/MIT - Simulation-Based Inference
["Flow Matching for Generative Modeling" Lipman et al]
["Stochastic Interpolants: A Unifying framework for Flows and Diffusions" Albergo et al]
u_t(x) = \int u_t(x|x_1) \frac{p_t(x|x_1) p_1(x_1)}{p_t(x)} \, dx_1
p_t(x) = \int p_t(x|x_1) q(x_1) \, dx_1
Intractable
Flow Matching
\frac{dz_t}{dt} = u^\phi_t(z_t)
x = z_0 + \int_0^1 u^\phi_t(z_t) dt
Continuity equation
\frac{d p(z_t)}{dt} = - \nabla \left( u^\phi_t(z_t) p(z_t) \right)
[Image Credit: "Understanding Deep Learning" Simon J.D. Prince]
Carolina Cuesta-Lazaro IAIFI/MIT - Simulation-Based Inference
Sample
Evaluate probabilities
Diffusion models
Carolina Cuesta-Lazaro IAIFI/MIT - Simulation-Based Inference
p(z_1|z_0)
p(z_0)
p(z_T)
p(z_2)
p(z_1)
p(z_2|z_1)
p(z_T|z_2)
Reverse diffusion: Denoise previous step
Forward diffusion: Add Gaussian noise (fixed)
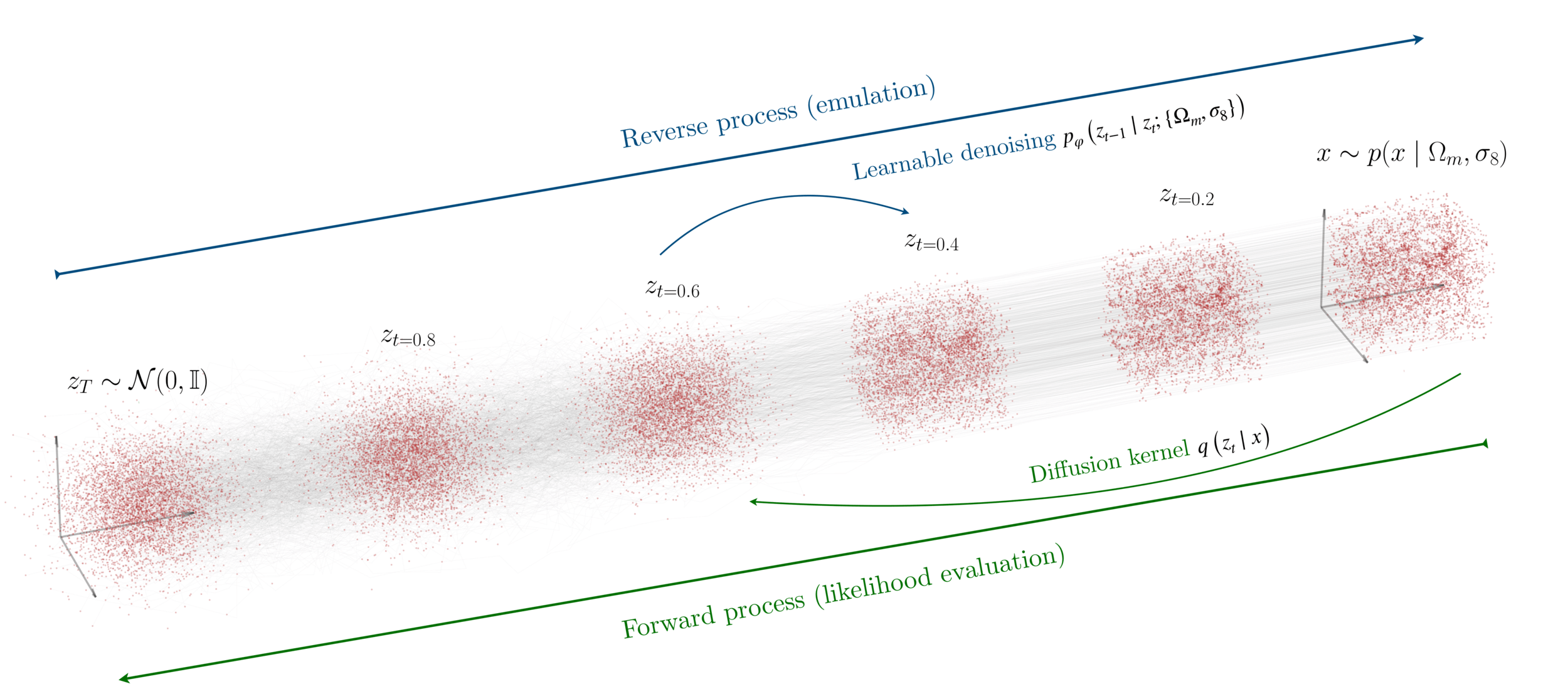
["A point cloud approach to generative modeling for galaxy surveys at the field level"
Cuesta-Lazaro and Mishra-Sharma
arXiv:2311.17141]
Siddharth Mishra-Sharma
Carolina Cuesta-Lazaro IAIFI/MIT - Simulation-Based Inference
Galaxies as point clouds
NLE
No implicit prior
Not amortized
Goodness-of-fit
Scaling with dimensionality of x
p(x|\theta)
NPE
p(\theta|x)
NRE
\frac{p(x|\theta)}{p(x)}
Amortized
Scales well to high dimensional x
Goodness-of-fit
Fixed prior
Implicit marginalization
\mathcal{L}(\phi) \approx -\frac{1}{N} \sum_{i=1}^N \log q_\phi(\theta_i \mid x_i)
\mathcal{L}(\phi) \approx -\frac{1}{N} \sum_{i=1}^N \log q_\phi(x_i \mid \theta_i )
No need variational distribution
No implicit prior
Implicit marginalization
Approximately normalised
\begin{split}
L &= - \frac{1}{N} \sum_{i=1}^N \left[ y_i \log(p_i) \right. \\
&\left. + (1 - y_i) \log(1 - p_i) \right]
\end{split}
Not amortized
Implicit marginalization
How good is your posterior?
Carolina Cuesta-Lazaro IAIFI/MIT - Simulation-Based Inference
Test log likelihood
["Benchmarking simulation-based inference"
Lueckmann et al
arXiv:2101.04653]
\mathbb{E}_{p(x,\theta)} \log \hat{p}(\theta \mid x)
Posterior predictive checks
Observed
Re-simulated posterior samples
Carolina Cuesta-Lazaro IAIFI/MIT - Simulation-Based Inference
Classifier 2 Sample Test (C2ST)
\mathrm{R} \sim p(\theta|x)
\mathrm{F} \sim \hat{p}(\theta|x)
Real or Fake?
Benchmarking SBI
Carolina Cuesta-Lazaro IAIFI/MIT - Simulation-Based Inference
["Benchmarking simulation-based inference"
Lueckmann et al
arXiv:2101.04653]
Classifier 2 Sample Test (C2ST)
Carolina Cuesta-Lazaro IAIFI/MIT - Simulation-Based Inference
["A Trust Crisis In Simulation-Based Inference? Your Posterior Approximations Can Be Unfaithful" Hermans et al
arXiv:2110.06581]
Much better than overconfident!
Coverage: assessing uncertainties
\int_\Theta \hat{p}(\theta \mid x = x_0) d\theta = 1 - \alpha
Carolina Cuesta-Lazaro IAIFI/MIT - Simulation-Based Inference
["A Trust Crisis In Simulation-Based Inference? Your Posterior Approximations Can Be Unfaithful" Hermans et al
arXiv:2110.06581]
Credible region (CR)
Not unique
High Posterior Density region (HPD)
Smallest "volume"
True value in CR with
1 - \alpha
probability
\theta^*
\mathcal{H}
Empirical Coverage Probability (ECP)
\mathrm{ECP} = \mathbb{E}_{p(x,\theta)} \left[ \mathbb{1} \left[ \theta \in \mathcal{H}_{\hat{p}(\theta|x)}(1-\alpha)\right] \right]
Carolina Cuesta-Lazaro IAIFI/MIT - Simulation-Based Inference
["Investigating the Impact of Model Misspecification in Neural Simulation-based Inference" Cannon et al arXiv:2209.01845 ]
Underconfident
Overconfident
Expected Coverage Probability (ECP)
\mathrm{ECP} = \mathbb{E}_{p(x,\theta)} \left[ \mathbb{1} \left[ \theta \in \mathcal{H}_{\hat{p}(\theta|x)}(1-\alpha)\right] \right]
Hard to find in high dimensions!
(x^*, \theta^*) \rightarrow
\left \{ \theta \in U \mid \hat{p}(\theta|x^*) \geq \hat{p}(\theta^*|x^*) \right \}
\theta^*
U
\mathcal{H}
\mathrm{ECP} = \mathbb{E}_{p(x,\theta)} \left[ \mathbb{1} \left[ \alpha_\mathrm{U}(\hat{p}, \theta^*, x^*) \geq \alpha \right]\right]
Carolina Cuesta-Lazaro IAIFI/MIT - Simulation-Based Inference
1-\alpha_\mathrm{U}
\leq 1-\alpha
Underconfident
Overconfident
["Sampling-Based Accuracy Testing of Posterior Estimators for General Inference" Lemos et al arXiv:2302.03026]
["Investigating the Impact of Model Misspecification in Neural Simulation-based Inference" Cannon et al arXiv:2209.01845 ]
Carolina Cuesta-Lazaro IAIFI/MIT - Simulation-Based Inference
Calibrated doesn't mean informative!
Always look at information gain too
\mathrm{ECP} = \mathbb{E}_{p(x,\theta)} \left[ \mathbb{1} \left[ \theta \in \mathcal{H}(\hat{p}, \alpha) \right] \right]
= \mathbb{E}_{p(\theta)} \left[ \mathbb{1} \left[ \theta \in \mathcal{H}(\hat{p}, \alpha) \right] \right]
\hat{p}(\theta \mid x) = p(\theta)
= \int_{\mathcal{H}(\hat{p}),\alpha} d\theta p(\theta)
\mathbb{E}_{p(x,\theta)} \left[ \log \hat{p}(\theta \mid x) - \log p(\theta) \right]
Carolina Cuesta-Lazaro IAIFI/MIT - Simulation-Based Inference
= 1 - \alpha
Carolina Cuesta-Lazaro IAIFI/MIT - Simulation-Based Inference
["A Trust Crisis In Simulation-Based Inference? Your Posterior Approximations Can Be Unfaithful" Hermans et al
arXiv:2110.06581]
["Calibrating Neural Simulation-Based Inference with Differentiable Coverage Probability" Falkiewicz et al
arXiv:2310.13402]
["A Trust Crisis In Simulation-Based Inference? Your Posterior Approximations Can Be Unfaithful" Hermans et al
arXiv:2110.06581]
Sequential SBI
Carolina Cuesta-Lazaro IAIFI/MIT - Simulation-Based Inference
["Benchmarking simulation-based inference"
Lueckmann et al
arXiv:2101.04653]
[Image credit: https://www.mackelab.org/delfi/]Carolina Cuesta-Lazaro IAIFI/MIT - Simulation-Based Inference
Sequential SBI
Sequential Neural Likelihood Estimation
["Sequential Neural Likelihood: Fast Likelihood-free Inference with Autoregressive Flows" Papamakarios et al
arXiv:1805.07226]
\theta \sim \overset{\sim}{p} (\theta)
Proposal (different from prior)
\overset{\sim}{p} (x,\theta) = p(x|\theta)\overset{\sim}{p}(\theta)
\mathbb{E}_{\overset{\sim}{p}(x,\theta)} \log q_\phi (x|\theta) =
\mathrm{D}_\mathrm{KL}(P(x) \mid \mid Q(x)) = \mathbb{E}_{P(x)} \left(\frac{\log P(x)}{\log Q(x)} \right)
= - \mathbb{E}_{\overset{\sim}{p} (\theta) } \left(\mathrm{D}_\mathrm{KL}(p(x|\theta) \mid \mid q_\phi(x|\theta) \right) + \mathrm{C}
Carolina Cuesta-Lazaro IAIFI/MIT - Simulation-Based Inference
SNLE
\overset{\sim}{p}(\theta \mid x_0) \propto p(\theta \mid x_0)\frac{\overset{\sim}{p}(\theta)}{p(\theta)}
["Fast -free Inference of Simulation Models with Bayesian Conditional Density Estimation" Papamakarios et al
arXiv:1605.06376]
["Flexible statistical inference for mechanistic models of neural dynamics." Lueckmann et al
arXiv:1711.01861]
Carolina Cuesta-Lazaro IAIFI/MIT - Simulation-Based Inference
Sequential can't be amortized!
Sequential Neural Posterior Estimation
SNPE
\theta \sim \overset{\sim}{p} (\theta)
Proposal (different from prior)
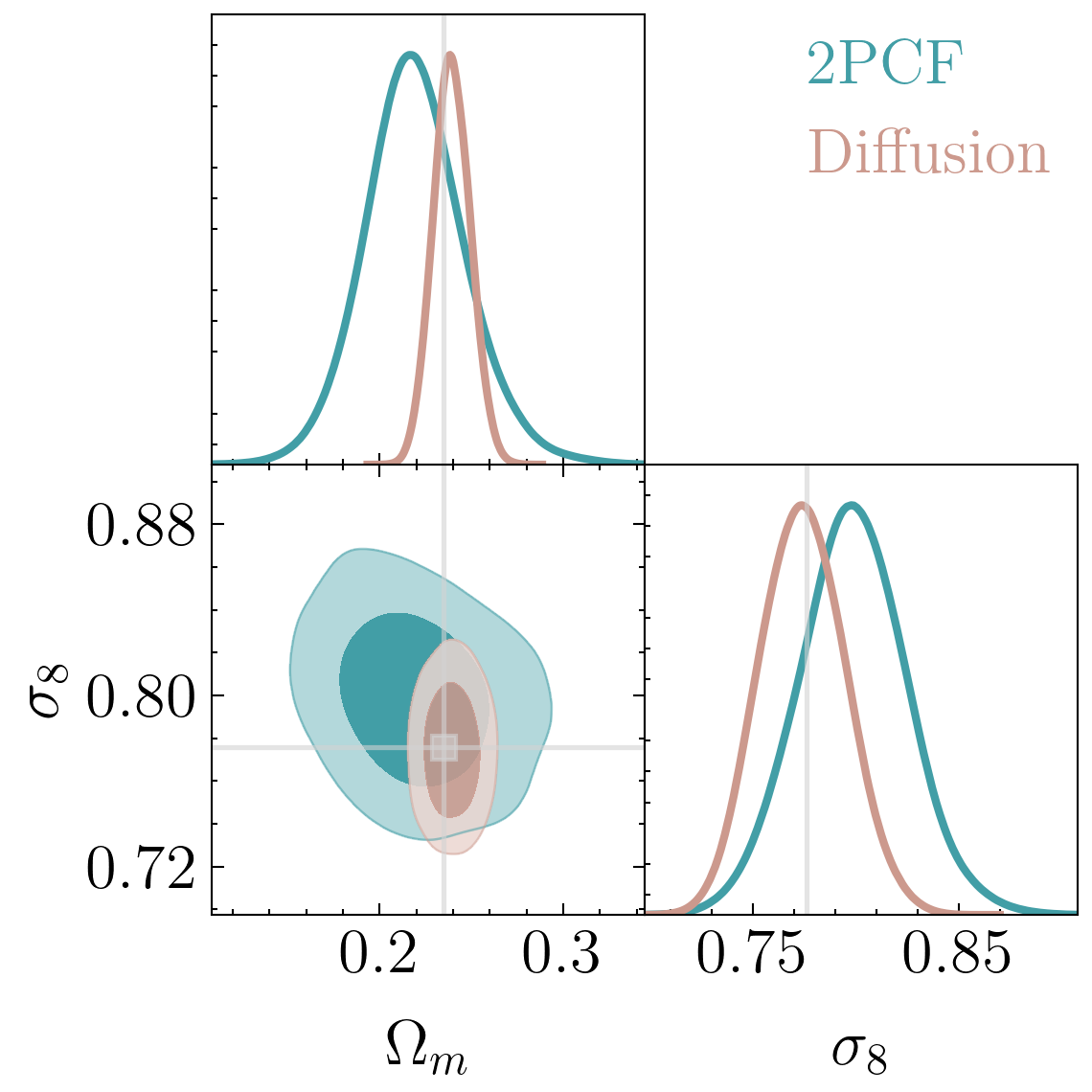
Real life scaling: Gravitational lensing
["A Strong Gravitational Lens Is Worth a Thousand Dark Matter Halos: Inference on Small-Scale Structure Using Sequential Methods" Wagner-Carena et al arXiv:2404.14487]
Carolina Cuesta-Lazaro IAIFI/MIT - Simulation-Based Inference
Current SBI limitations
Carolina Cuesta-Lazaro IAIFI/MIT - Simulation-Based Inference
["All-in-one simulation-based inference" Gloeckler et al arXiv:2404.09636]
Model all conditionals at once!
All-in-one: The Simformer
Carolina Cuesta-Lazaro IAIFI/MIT - Simulation-Based Inference
["All-in-one simulation-based inference" Gloeckler et al arXiv:2404.09636]
Score based diffusion model with sampled conditional masks
Carolina Cuesta-Lazaro IAIFI/MIT - Simulation-Based Inference
Model mispecification
Carolina Cuesta-Lazaro IAIFI/MIT - Simulation-Based Inference
["Investigating the Impact of Model Misspecification in Neural Simulation-based Inference" Cannon et al arXiv:2209.01845]
More misspecified
SBI Resources
Carolina Cuesta-Lazaro IAIFI/MIT - Simulation-Based Inference
"The frontier of simulation-based inference" Kyle Cranmer, Johann Brehmer, and Gilles Louppe
Github repos
Review
cuestalz@mit.edu
Book
"Probabilistic Machine Learning: Advanced Topics" Kevin P. Murphey
SBI-IAIFI2024-SummerSchool
By carol cuesta
