Will ML shape the future of cosmology?
A journey through obstacles and potential approaches to overcoming them
Carolina Cuesta-Lazaro
IAIFI Fellow (MIT/CfA)
The golden days of Cosmology:
A five parameter Universe
\Omega_m
\Omega_b
\Omega_\Lambda
A_s
n_s
Initial Conditions
(Inflation)
Dynamics
Dark energy
Dark matter
Ordinary matter
Amplitude initial density field
Scale dependence
t = 400,000 years
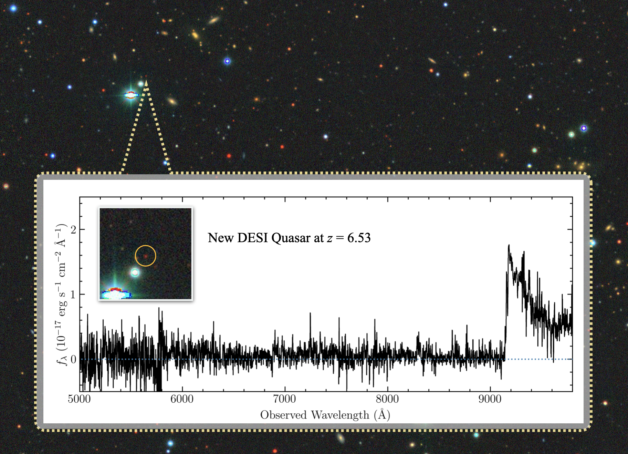
DESI: Dark Energy Spectroscopic Instrument
~35 Million spectra!
(Image Credit: Jinyi Yang, Steward Observatory/University of Arizona)
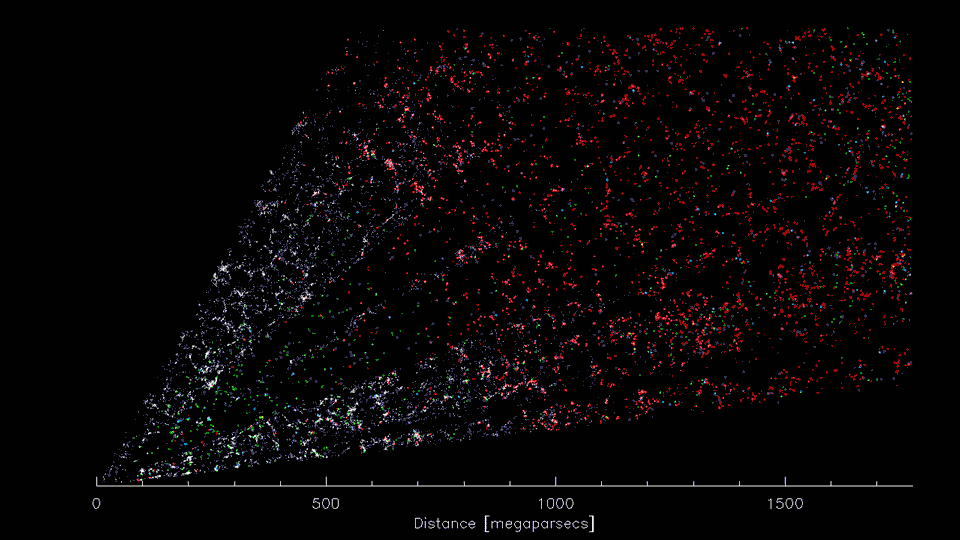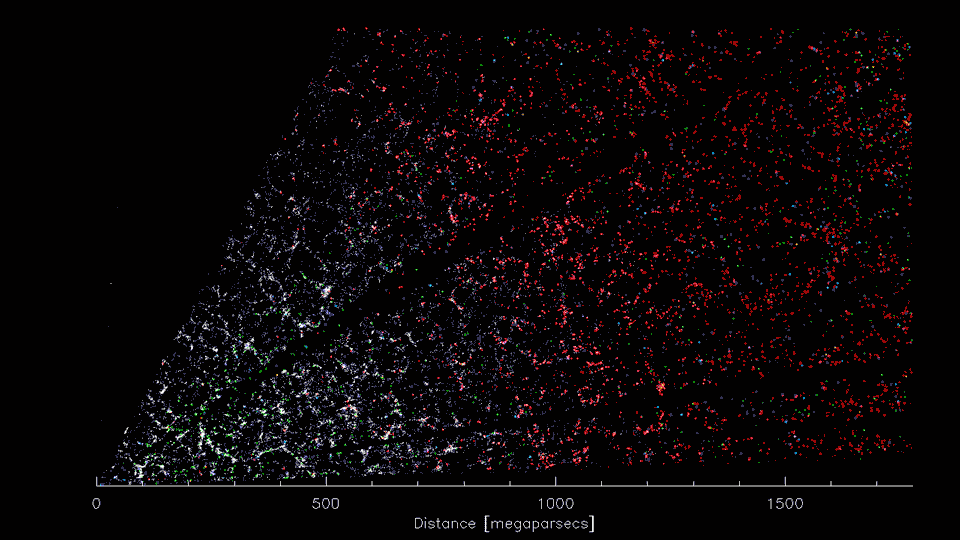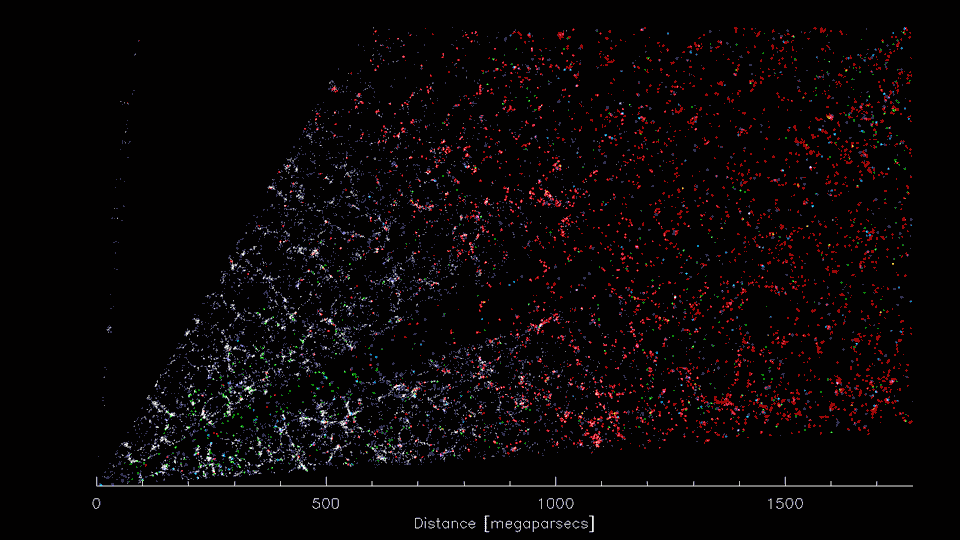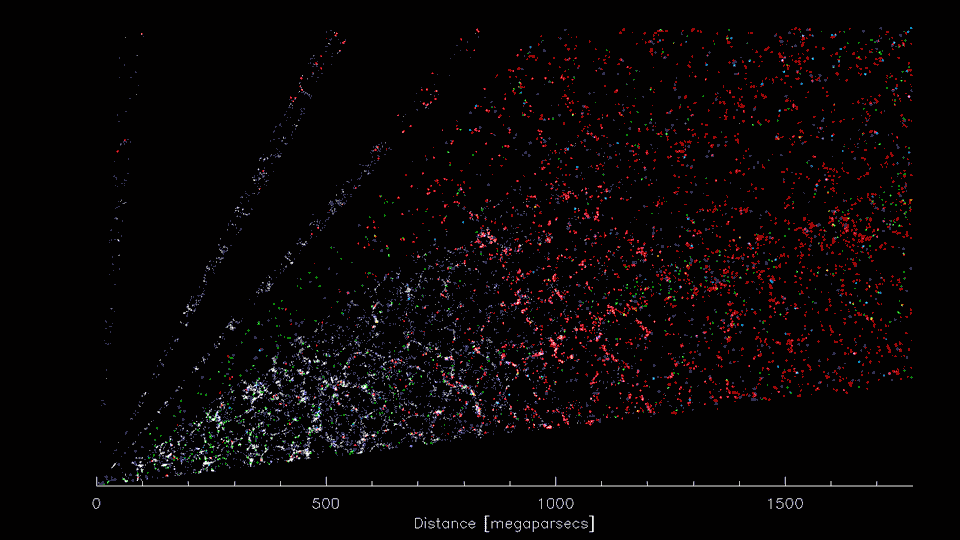
(Image Credit: D. Schlegel/Berkeley Lab using data from DESI)
Neutrino mass hierarchy
Primordial Non-gaussianity
Galaxy formation
Large scale modifications of gravity
using growth to detect the existence of fifth forces
LSS might provide the most accurate measurement
to probe the physics of inflation (single/multi field, particle content)
not only a nuisance to margnilize over!
1
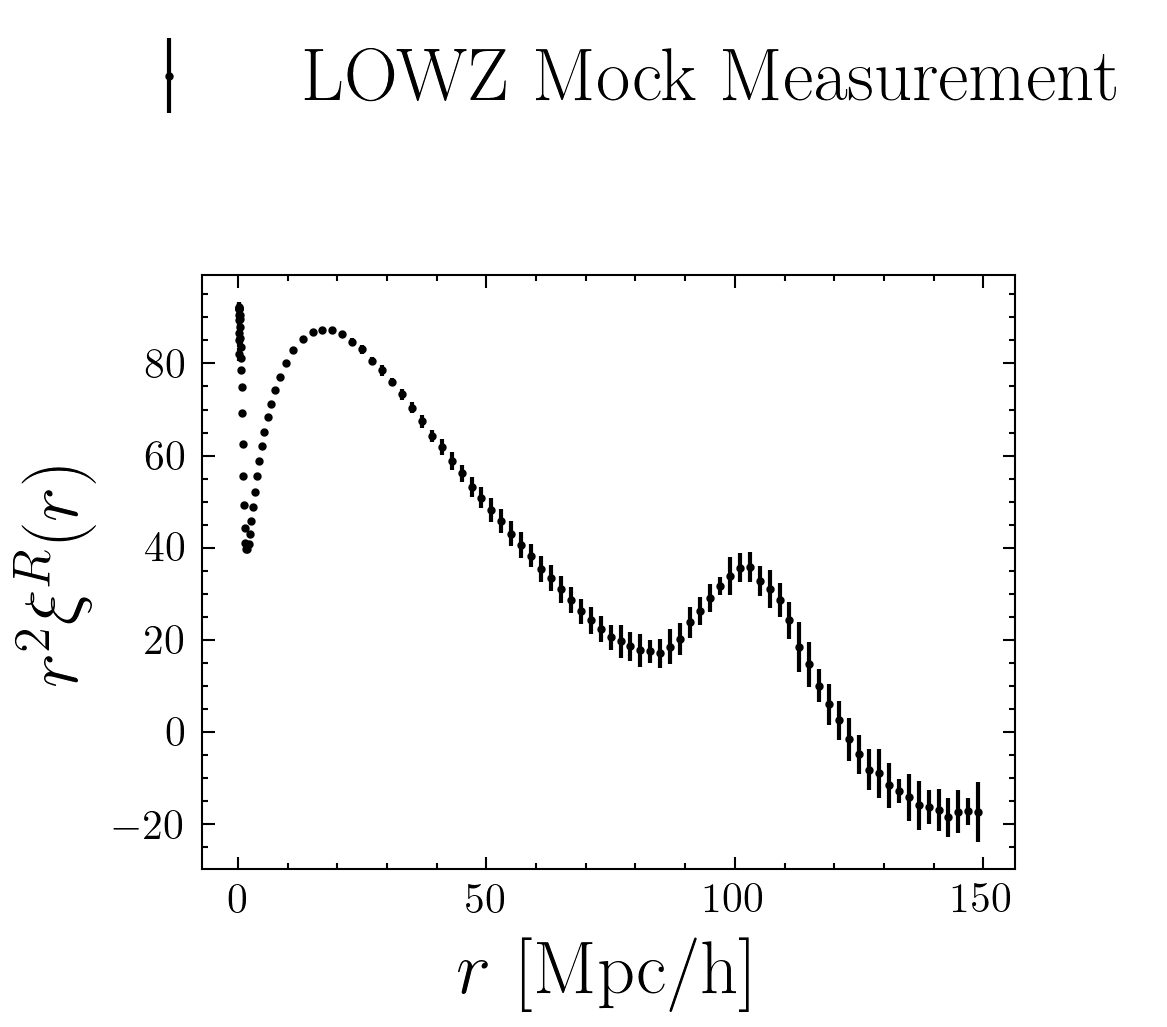
Observe galaxies
4
Pick your favourite analytical likelihood (Gaussian!)
5
Compute ~1Million times to get posterior
Constrain cosmology 101
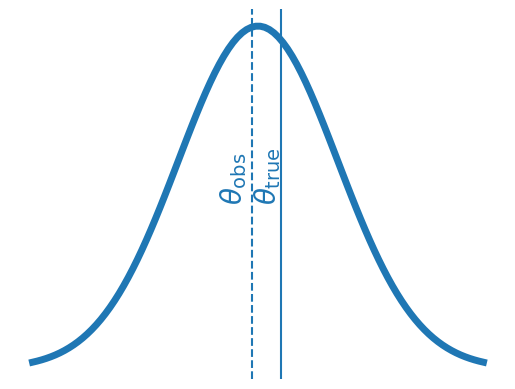
Missing Information!
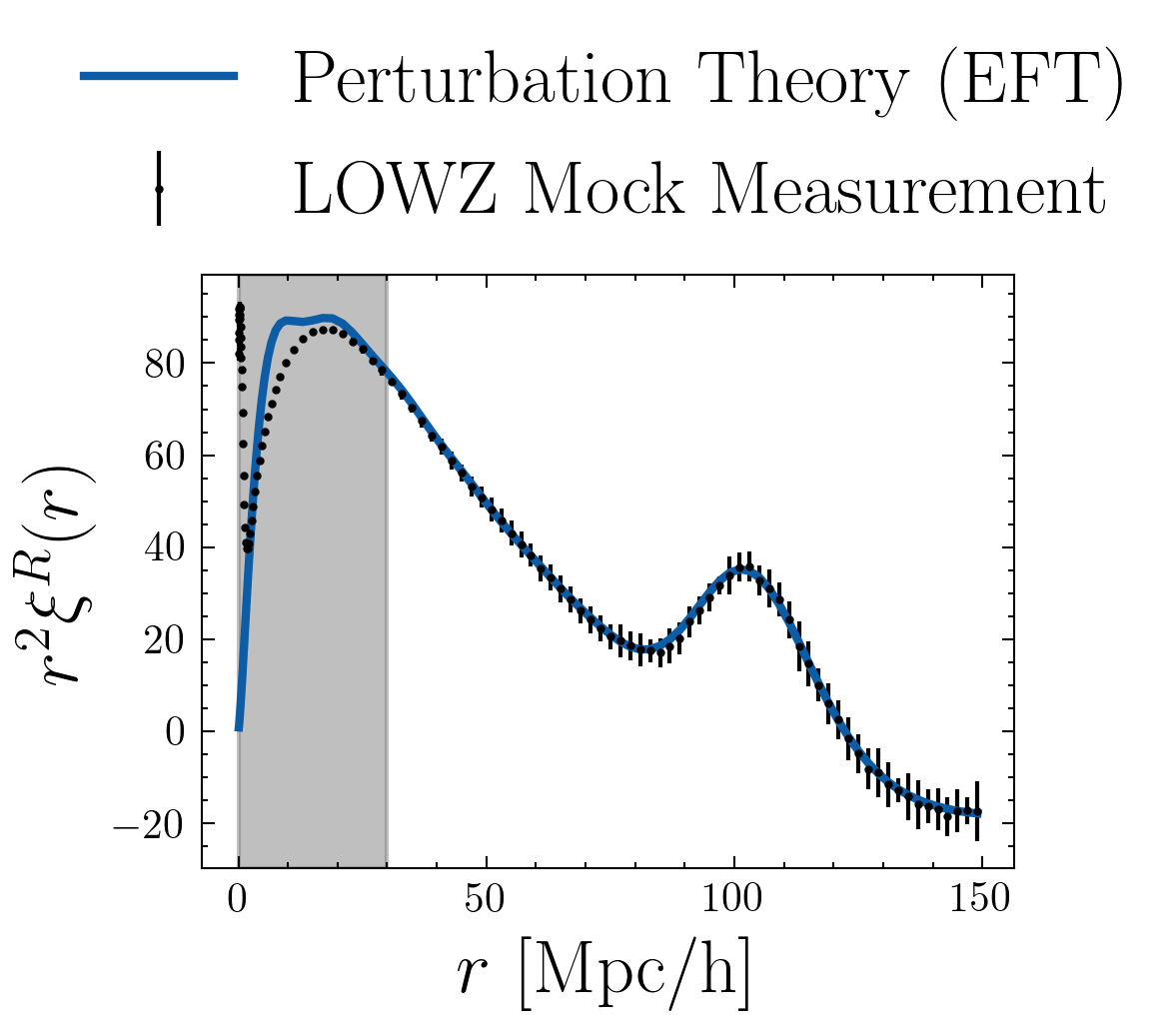
Perturbation Theory inaccurate / hard to compute
Is it always true?
3
Work on your analytical theory
2
Count pairs as a function of distance
\bar{\xi}(R_s)
R_s
1
1
1
2
2
4
5
5
5
3
Enrique Paillas
Waterloo
arXiv:2209.04310
How much information do we lose?
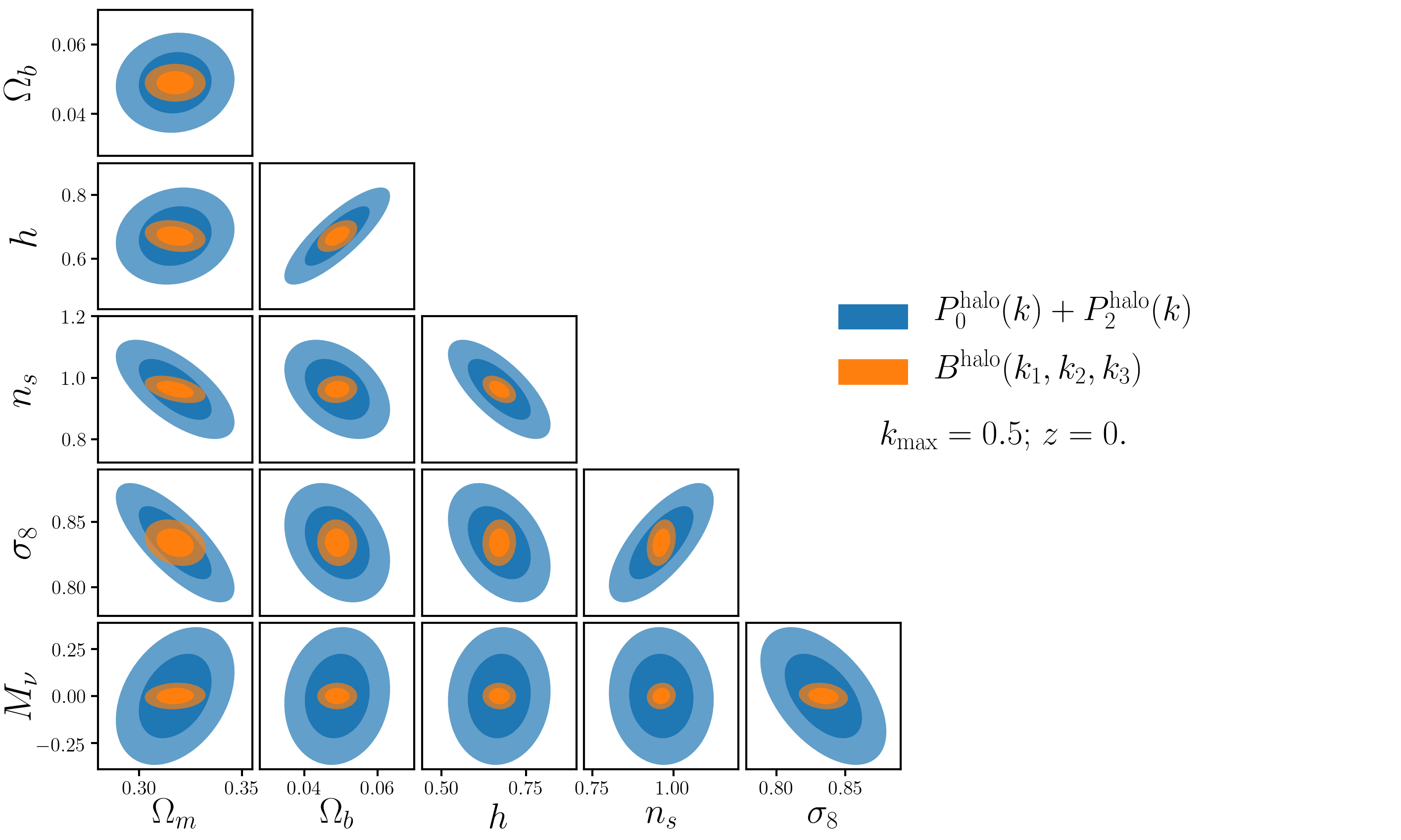
Bispectrum
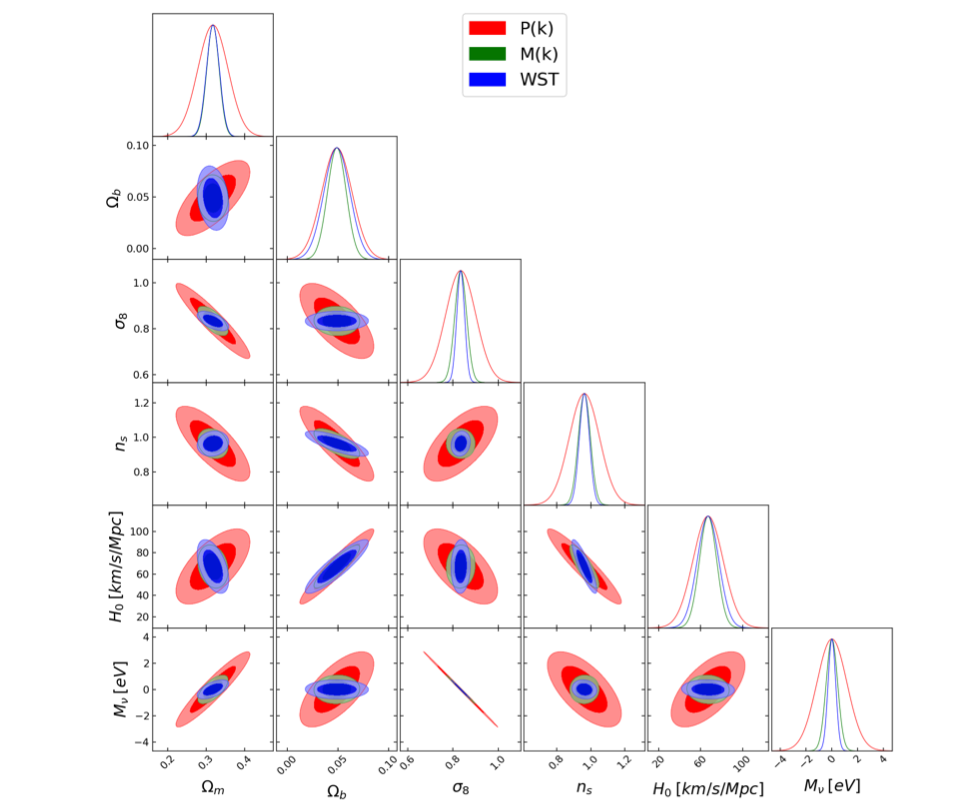
Wavelet Scattering Transform
arXiv:1909.11107
arXiv:2204.13717
Marked Power Spectrum
arXiv:2206.01709
ML for Large Scale Structure:
A wish list
Generative models
Learn p(x)
Sample simulations with different parameter values quickly
1
Evaluate their likelihood the field level
2
Do not make assumptions on the likelihood's form
3
Latent Generative Models: Normalising flows
x = f(z), \, z = f^{-1}(x)
p(\mathbf{x}) = p_z(f^{-1}(\mathbf{x})) \left\vert \det J(f^{-1}) \right\vert
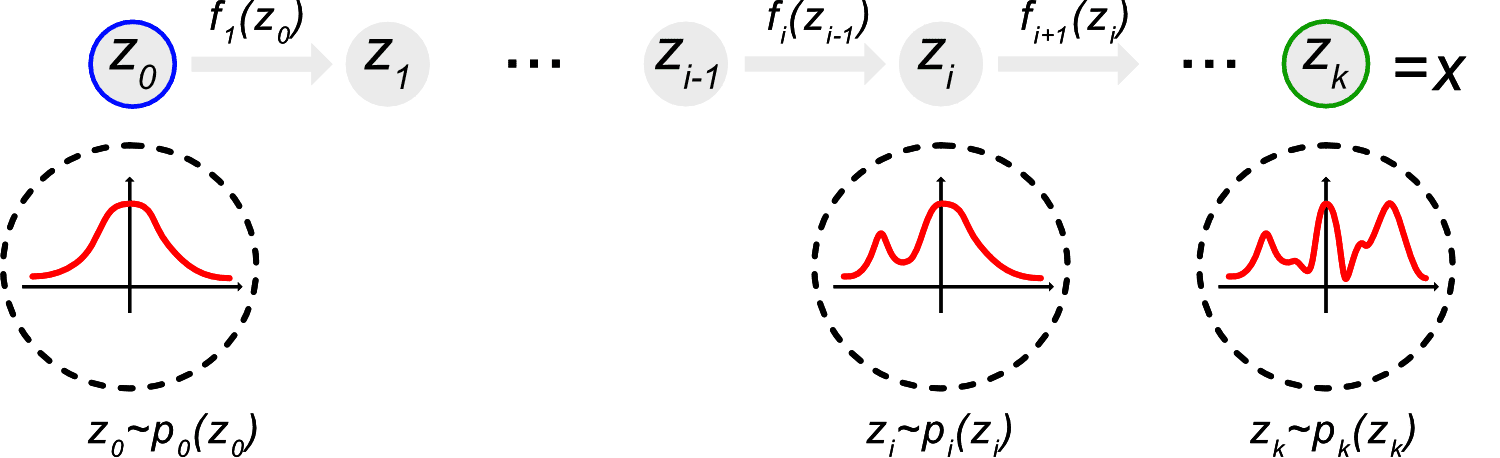
(Image Credit: Phillip Lippe)
p(x) = \int dz \, p(x|z)
z_T
z_{0}
z_{1}
Diffusion Models
Reverse diffusion: Denoise previous step
Forward diffusion: Add Gaussian noise (fixed)
z_{2}
p_\theta(z_{t-1}|z_t)
q(z_t|z_{t-1})
Siddharth Mishra-Sharma
Should we be using CNNs?
Galaxy positions
+ Magnitudes, velocities ...
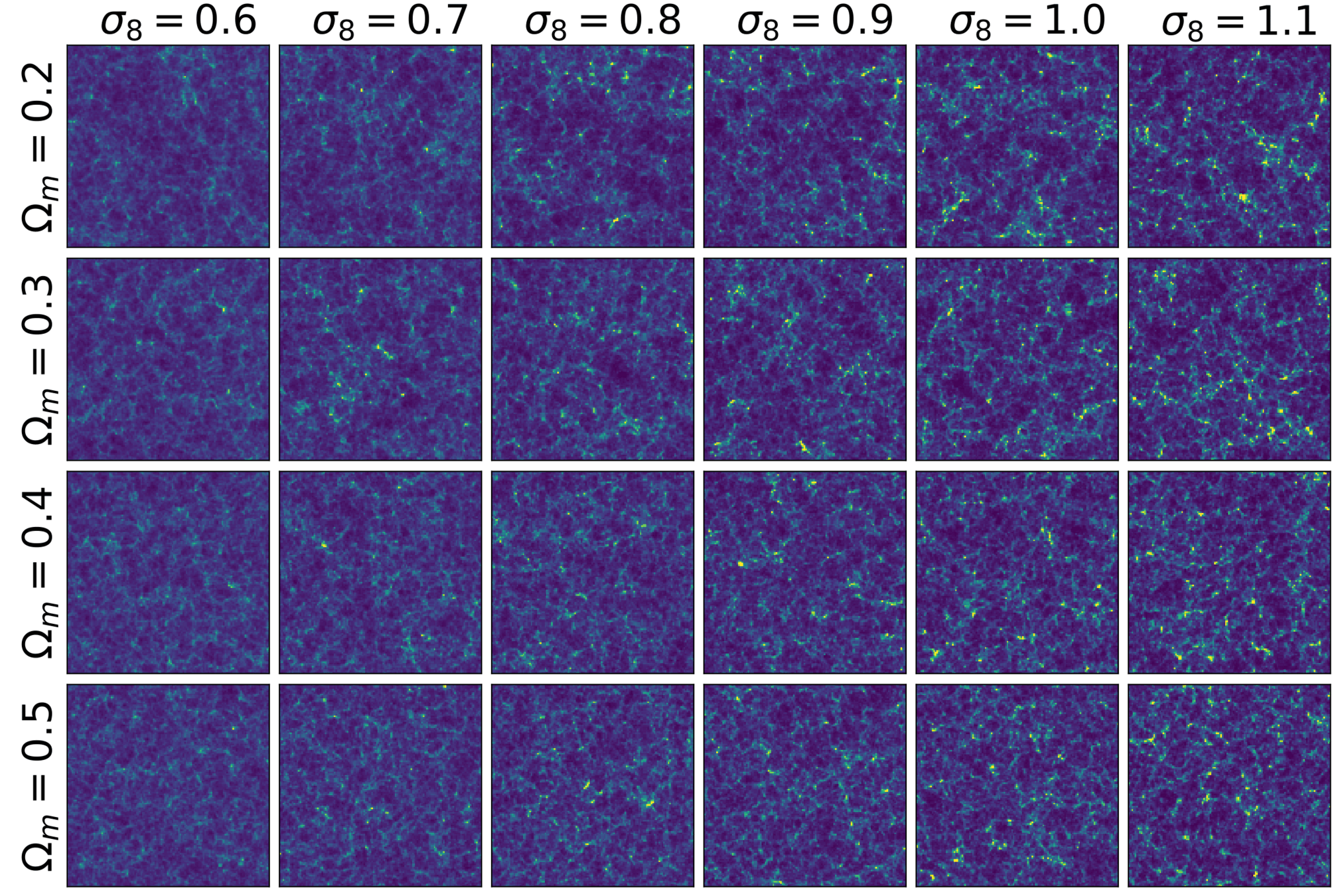
Dark matter density field
(Image Credit: SIMBIG)
z_T
z_{0}
z_{1}
Diffusion on sets
z_{2}
p_\theta(z_{t-1}|z_t)
q(z_t|z_{t-1})
Reverse diffusion: Denoise previous step
Forward diffusion: Add Gaussian noise (fixed)
p_\theta(z_{t-1}|z_t) = \mathcal{N}(z_{t-1}|\mu_\theta(z_t, t), \sigma_t^2 \mathcal{I})
Set
Set
\mu_\theta
Neural network
z_{t-1}
z_{t}
Credit: Siddharth Mishra-Sharma
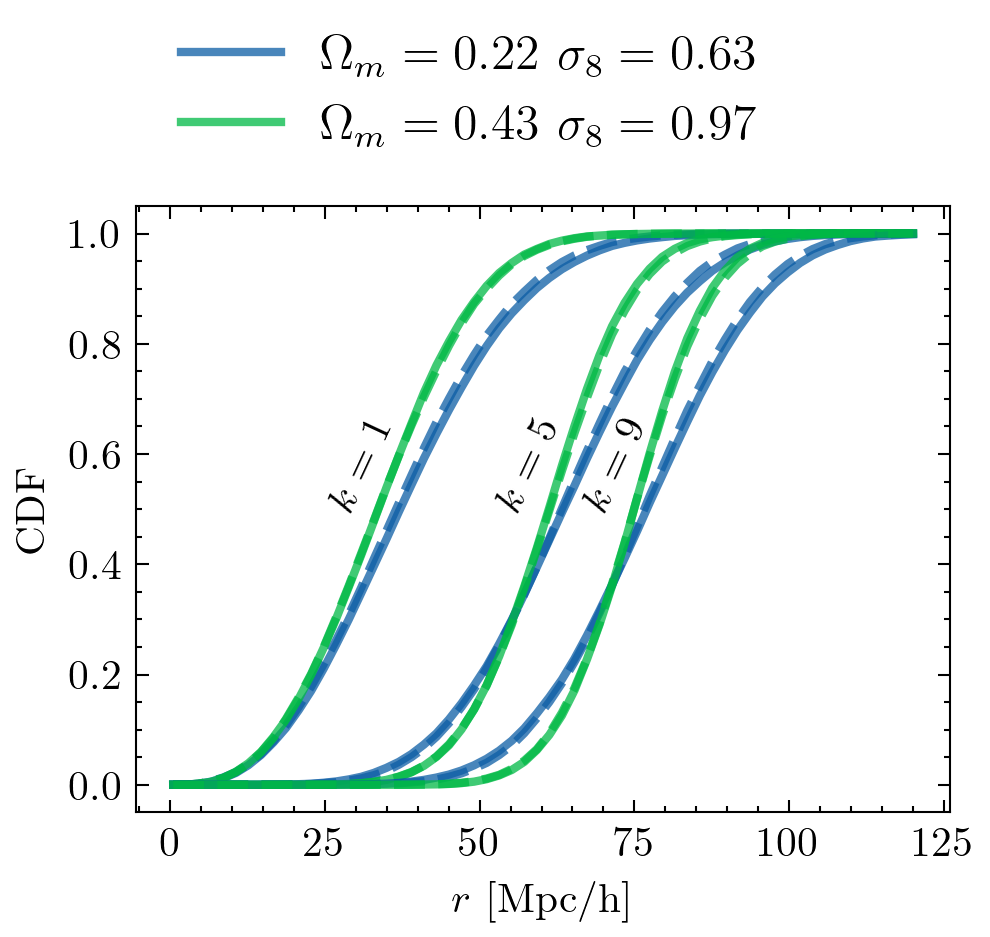
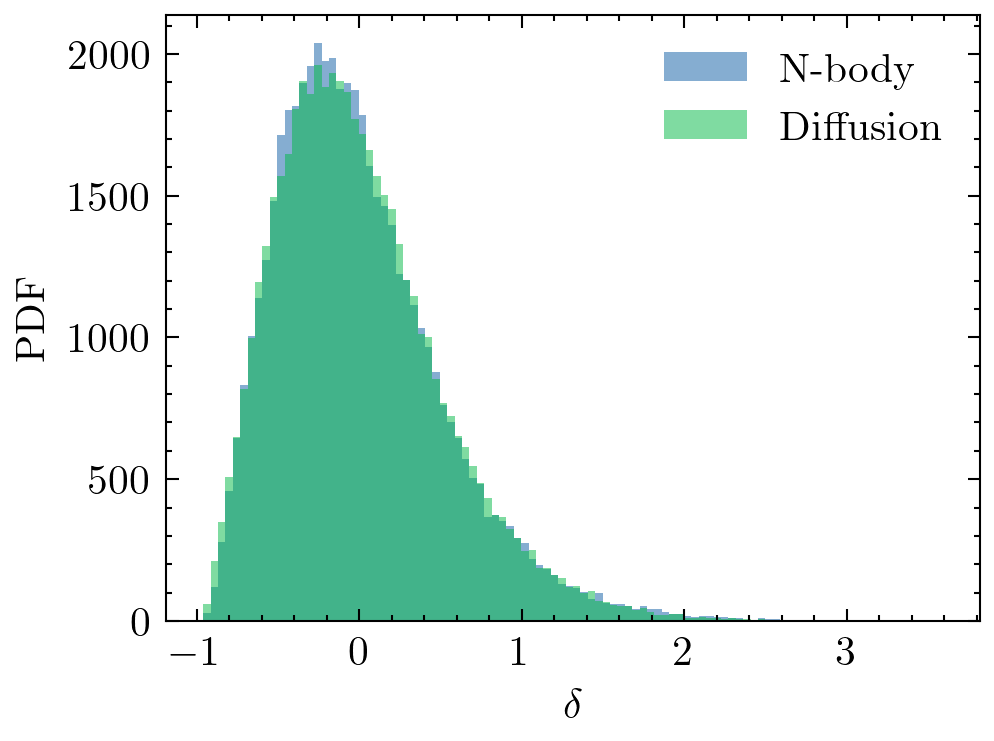
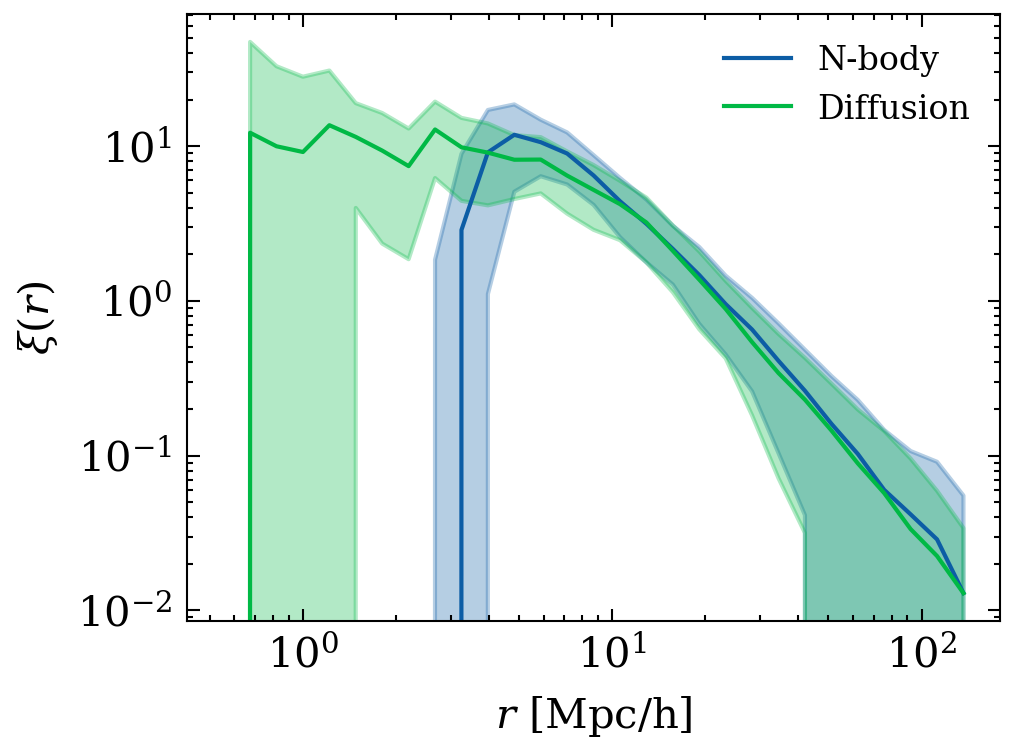
+ Galaxy formation
+ Observational systematics (Cut-sky, Fiber collisions)
+ Lightcone, Redshift Space Distortions....
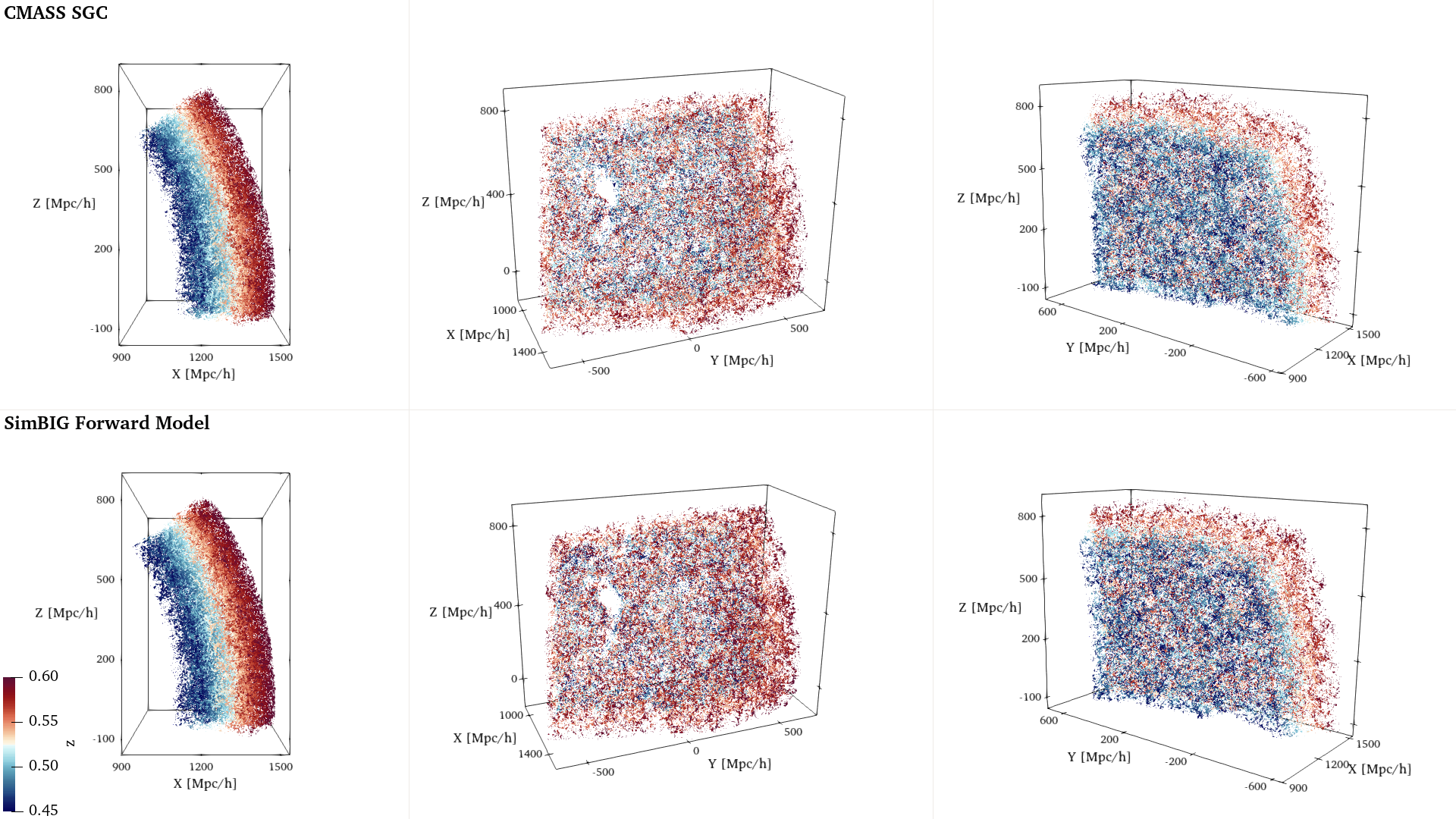
Forward Model
N-body simulations
Observations
SIMBIG arXiv:2211.00723
We can simulate the observable Universe, we just need hydrodynamical simulations
25 \, h^{-1}\mathrm{Mpc}
What are subresolution models?
10^{10} - 10^{11} M_\odot
Super massive black hole seeding in dark matter halos
BH feedback impacts galactic scales
Black holes can also growth through mergers
Effective models of astrophysical processes needed due to limited numerical resolutions or limited physical models
they can even teleport!
We can't model galaxy formation, how do we make our models robust?
Robust Summarisation
\mathcal{L} = I(S(x_\mathrm{sims})|\theta_\mathrm{sims}) + \blue{\lambda p_\mathrm{sims}(S(x_\mathrm{obs}))}
S:
Summariser (neural net)
(\theta_\mathrm{sims}, x_\mathrm{sims})
x_\mathrm{obs}
\mathcal{L} = I(S(x_\mathrm{sims})|\theta_\mathrm{sims})
Increase the evidence of the observations
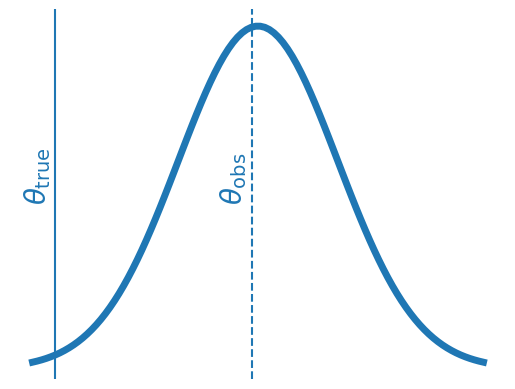
Sims misspecified
What ML can do for cosmology
- ML to accelerate non-linear predictions and density estimation
- Can ML extract **all** the information that there is at the field-level in the non-linear regime?
- Compare data and simulations, point us to the missing pieces?
cuestalz@mit.edu
Graph Neural Networks in a nutshell
\mathcal{G} = h^{L}_i, e^{L}_{ij} \rightarrow h^{L+1}_i, e^{L+1}_{ij}
e^{L+1}_{ij} = \phi_e(e^L_{ij}, h^L_i, h^L_j)
h^{L+1}_{i} = \phi_h( h^L_i, \mathcal{A}_j e^{L+1}_{ij})
edge embedding
node embedding
e_{ij}
h_i = \{\mathrm{positions}, \mathrm{velocities}...\}
h_j
Introducing homogeneity and isotropy
Redshift Space Distortions break isotropy
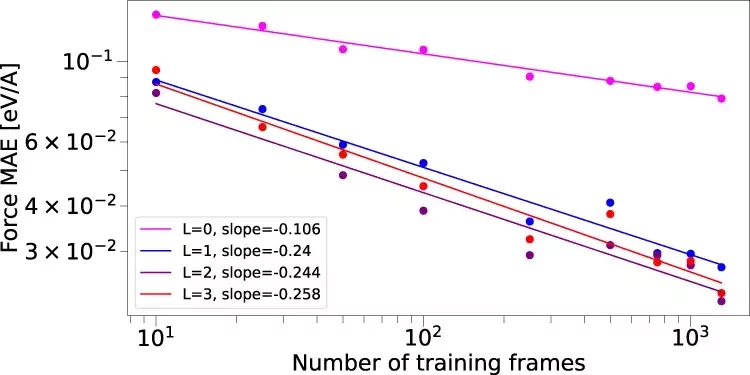
(Credit: E(3)-equivariant graph neural networks for data-efficient and accurate interatomic potentials)
arXiv:2202.05282
Normalising flows as generative models
arXiv:2202.05282
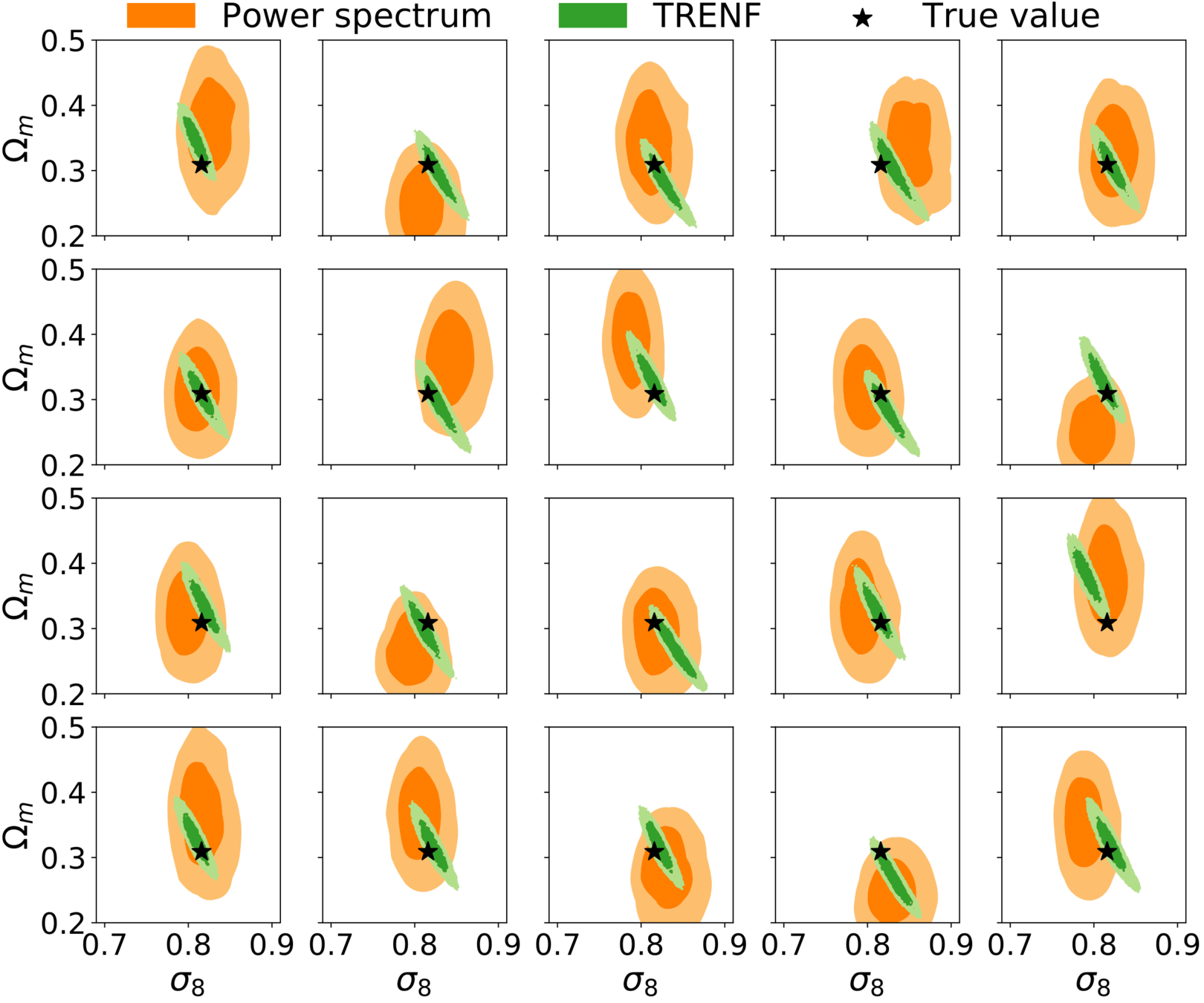
- Fast theory models
- Do all these summaries combined get all info?
- Optimal information extraction
- Density estimation
- Improving current simulations?
- How can we deal with model mispecification?
ML to the rescue for
arXiv:2107.00630
- \log p(x) \leq -\mathrm{VLB}(x) =
\purple{\mathrm{Prior Loss}} + \gray{\mathrm{Recon Loss}} + \blue{\mathrm{Diffusion Loss}}
\purple{\mathrm{Prior Loss} = D_\mathrm{KL} (q(z_T|x)|p(z_T))}
\gray{\mathrm{Recon Loss} = \mathbb{E}_{q(z_0|x)} [ -\log p(x|z_0)]}
\blue{\mathrm{Diffusion Loss} = }
\blue{\sum_{t} D_\mathrm{KL} \left[ q(z_{t-1}|z_{t},x) || p_\theta (z_{t-1}|z_{t}) \right]}
Gaussian,
fully known
Also Gaussian,
but learned mean
Invariance vs Equivariance
r
\theta
\phi
Invariance
Scalar interactions
r
Equivariance
What can we do with vectors?
Tensor products
v_i
v_j
Mario Geiger
Siddharth Mishra-Sharma
Making homogeneous and isotropic universes
p(x)
\mu_\theta(z_t,t)
p(z_T)
Invariant
to rotations and translations
Equivariant
Invariant
=
p(
)
p(
p(
)
Invariant
=
p(
)
p(
=
p(
)
p(
(\vec{\theta}_i, z_i)
z_i = z_{\mathrm{Cosmological} }
+ z_{\mathrm{Doppler}}
\chi(z) = \int_0^z \frac{dz'}{H(z')}
+ \frac{v_{\mathrm{pec}}}{aH(a)}
\chi_i
Copy of deck
By carol cuesta
