Carol Cuesta-Lazaro

IAIFI Fellow - Institute for Artificial Intelligence and Fundamental Interactions (MIT)
Deep Generative AI:
Inteligencia Artificial y sus aplicaciones en Física
Latam
Summer School
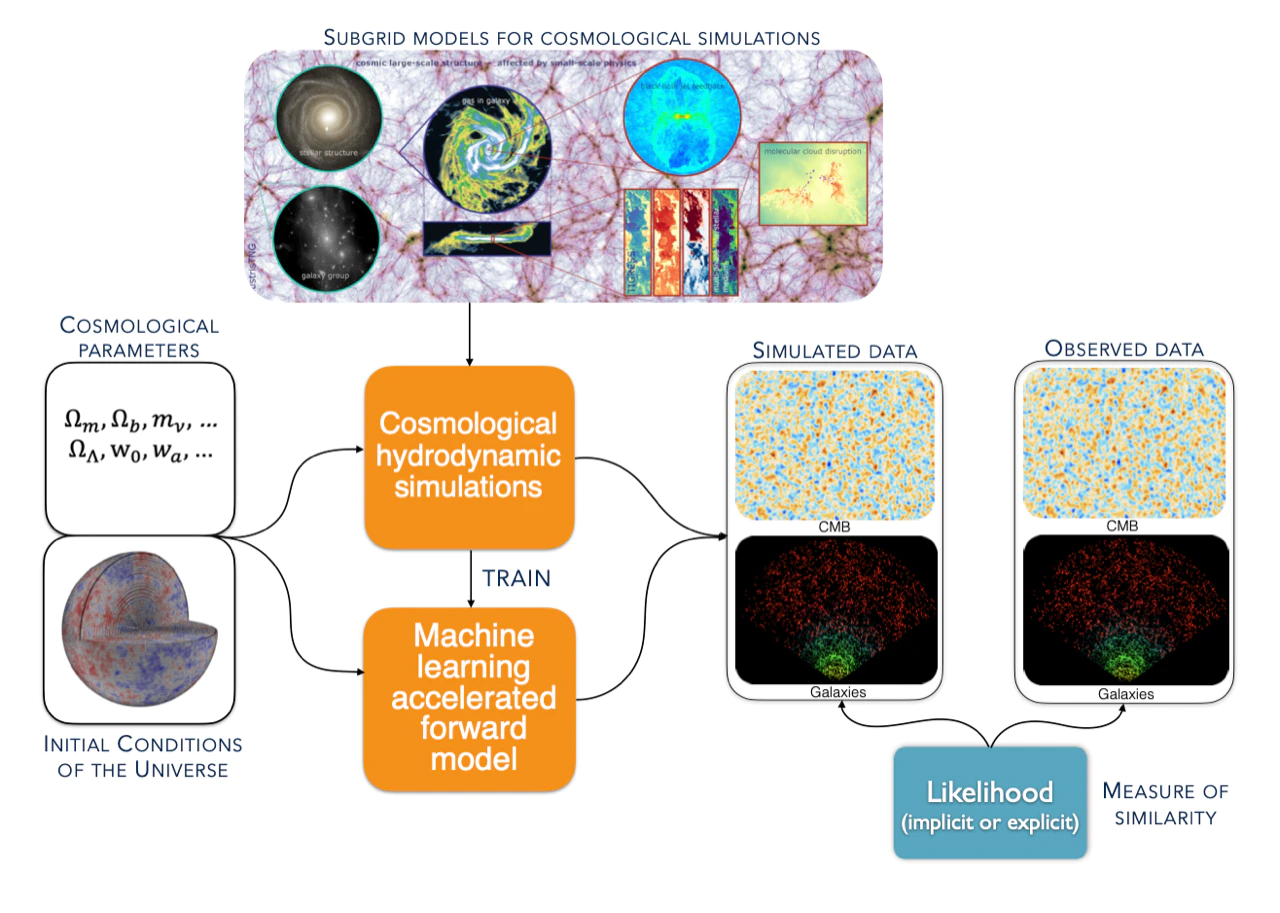
Las condiciones iniciales del Universo
Laws of gravity
Distribucion 3D de galaxias
Cuales son las CIs de NUESTRO Universo?
non-Gaussianidad primordial?
Inflacion
Galaxy formation

Distribucion 3D de materia oscura
Modificar GR en escalas grandes?
Como se forman las galaxias?














jerarquia de las masas de neutrinos?
AI y Fisica
- Que son los modelos generativos?
- Mis favoritos: likelihood-based
- Normalising flows
- Variational Autoencoders
- Variational Inference
- Diffusion models
Generar vs Discriminar
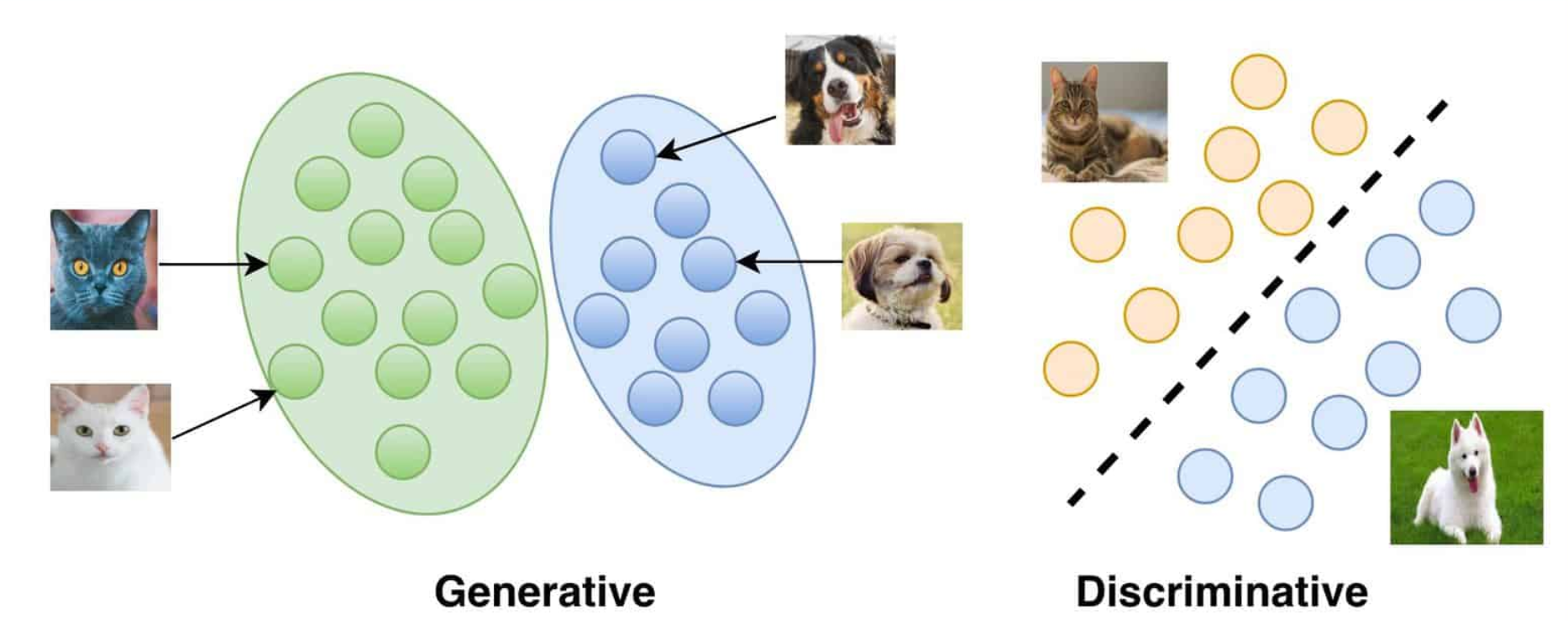
https://vitalflux.com/generative-vs-discriminative-models-examples/
El salón de la Fama

A teddy bear wearing a motorcycle helmet and cape is standing in front of Loch Awe with Kilchurn Castle behind him driving a speed boat near the Golden Gate Bridge

https://parti.research.google

Modelos generativos en Fisica
Emular procesos complejos en dimensiones altas

arXiv:2206.04594
Super resolución
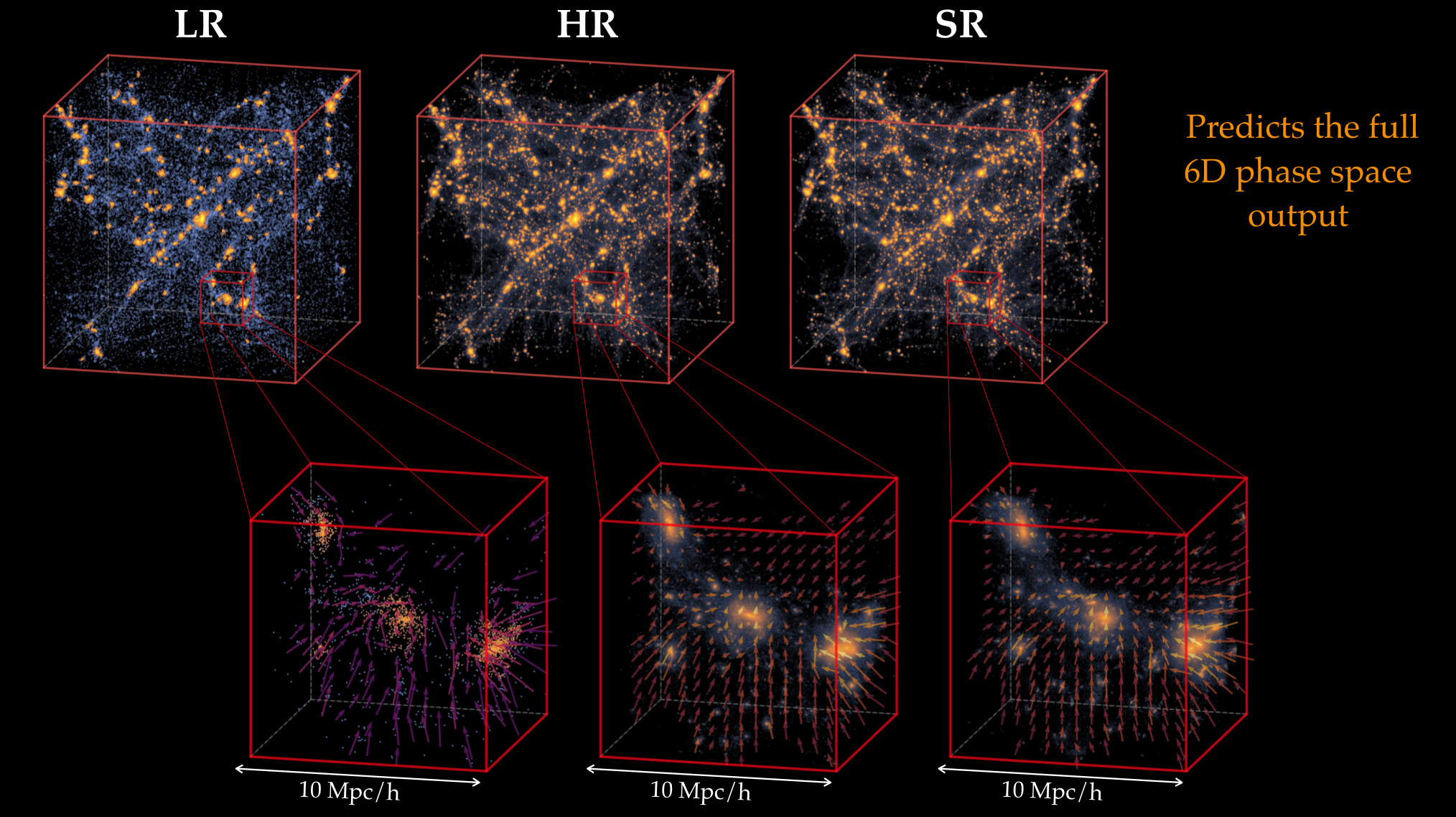
arxiv:2010.06608
Modelos generativos en Fisica
Detectar anomalias

arxiv:2010.14554
Modelos generativos en Fisica
Comparar datos y simulaciones de forma optima:
Simulation-based Inference
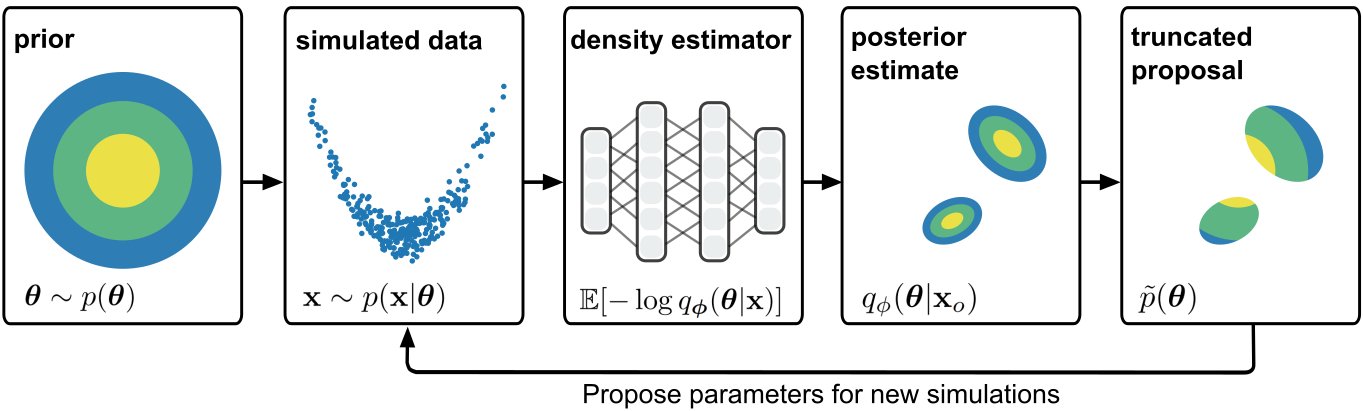
Modelos generativos en Fisica
arXiv:1911.01429
Modelar incertidumbres


arxiv:2010.14554
Modelos generativos en Fisica
Universo actual
Condiciones Iniciales
Representar priors complejos
arxiv:2206.14820
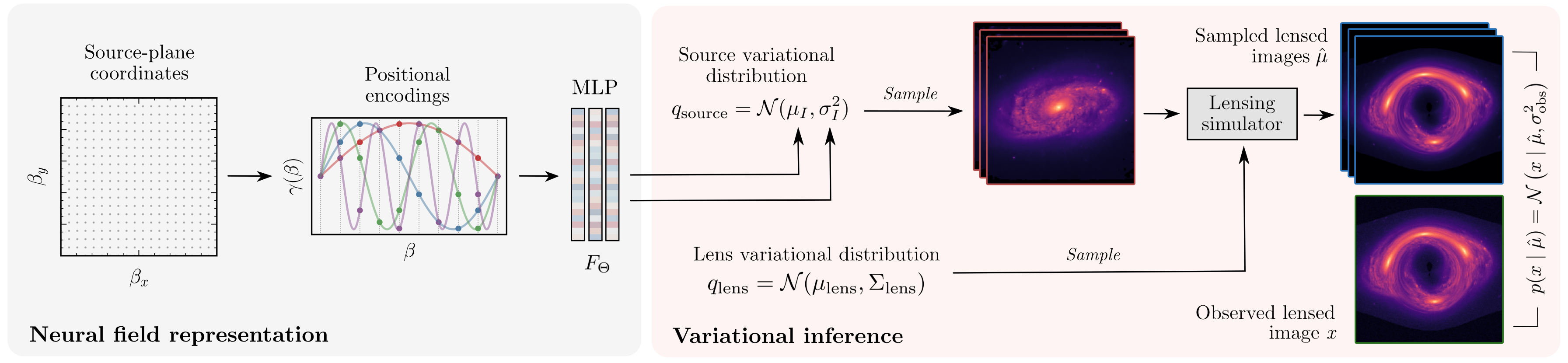
Modelos generativos en Fisica

prior en galaxies?
Lente
gravitacional
Modelos Generativos

Datos
Una PDF que podamos parametrizar
Maximizar el likelihood!
(o algo que se le parece)
2. Generar muestras


1. Estimar densidades
Maximizar el likelihood (o algo que se le parezca)
Posterior
Likelihood
Prior
Evidence

Distribucion base
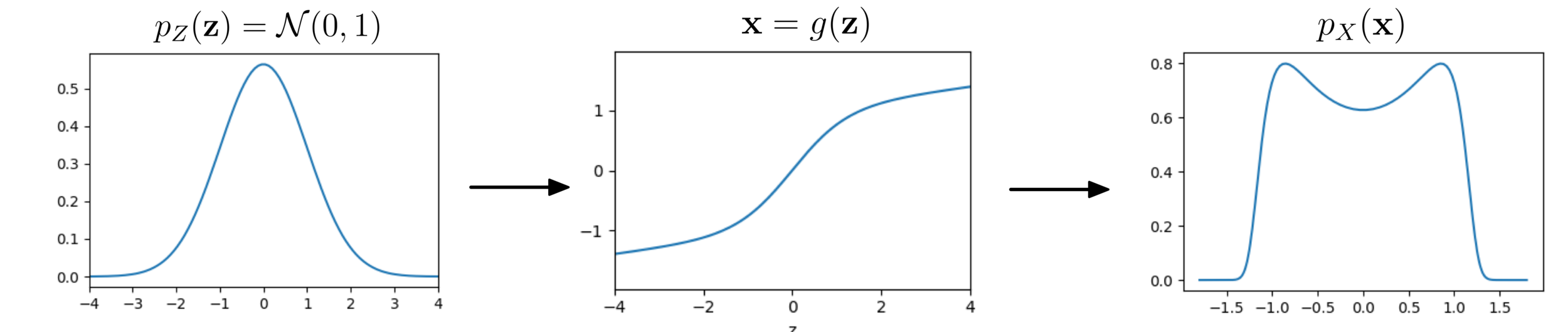
Distribucion destino (target)


Normalising flows: Cambio de variables
Transformacion Invertible


Transformacion Box-Muller: Normalising flows en 1934
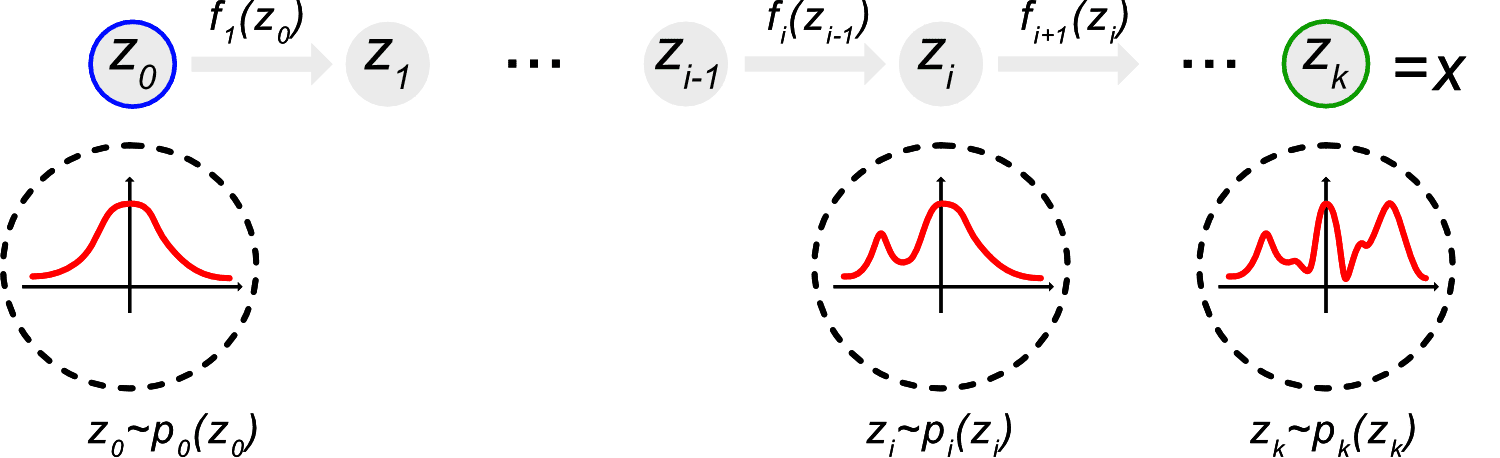
(Image Credit: Phillip Lippe)
z: Variables latentes
Normalising flows
Normalising flows
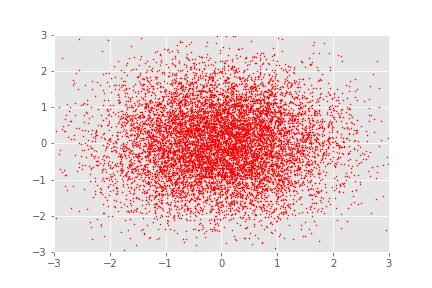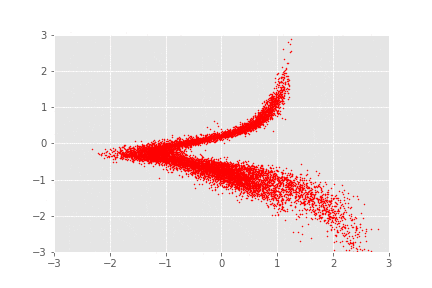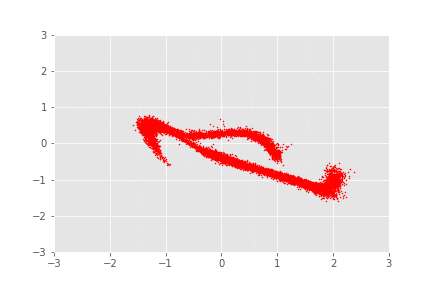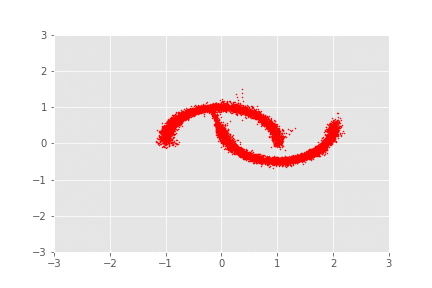
No es tan fácil encontrar funciones invertibles!
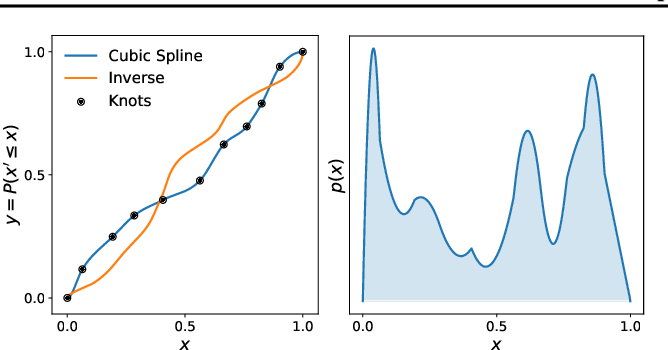
Splines
arXiv:2202.05282
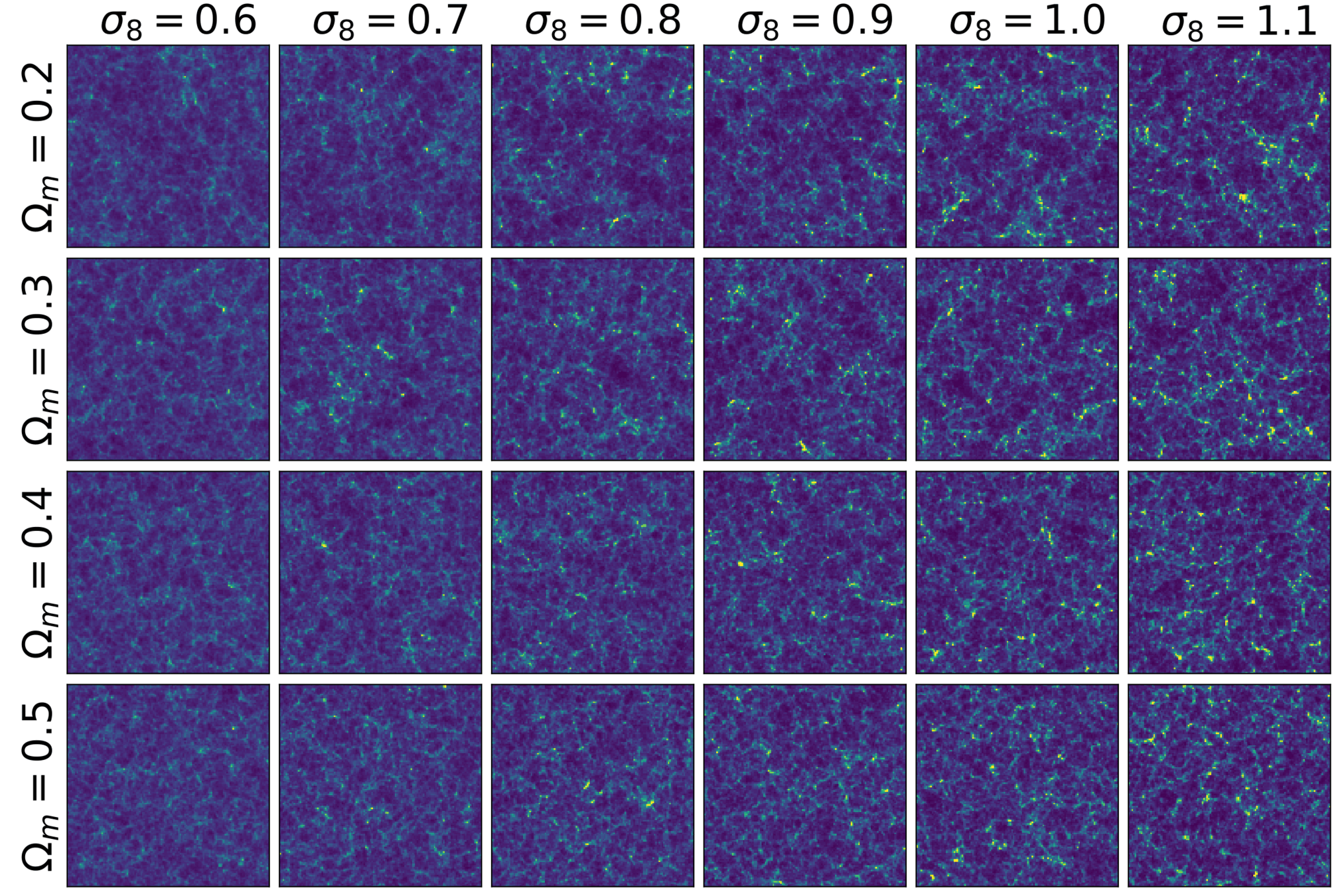
Normalising flows en cosmologia

Normalising flows en cosmologia
arXiv:2202.05282
arXiv:2202.05282
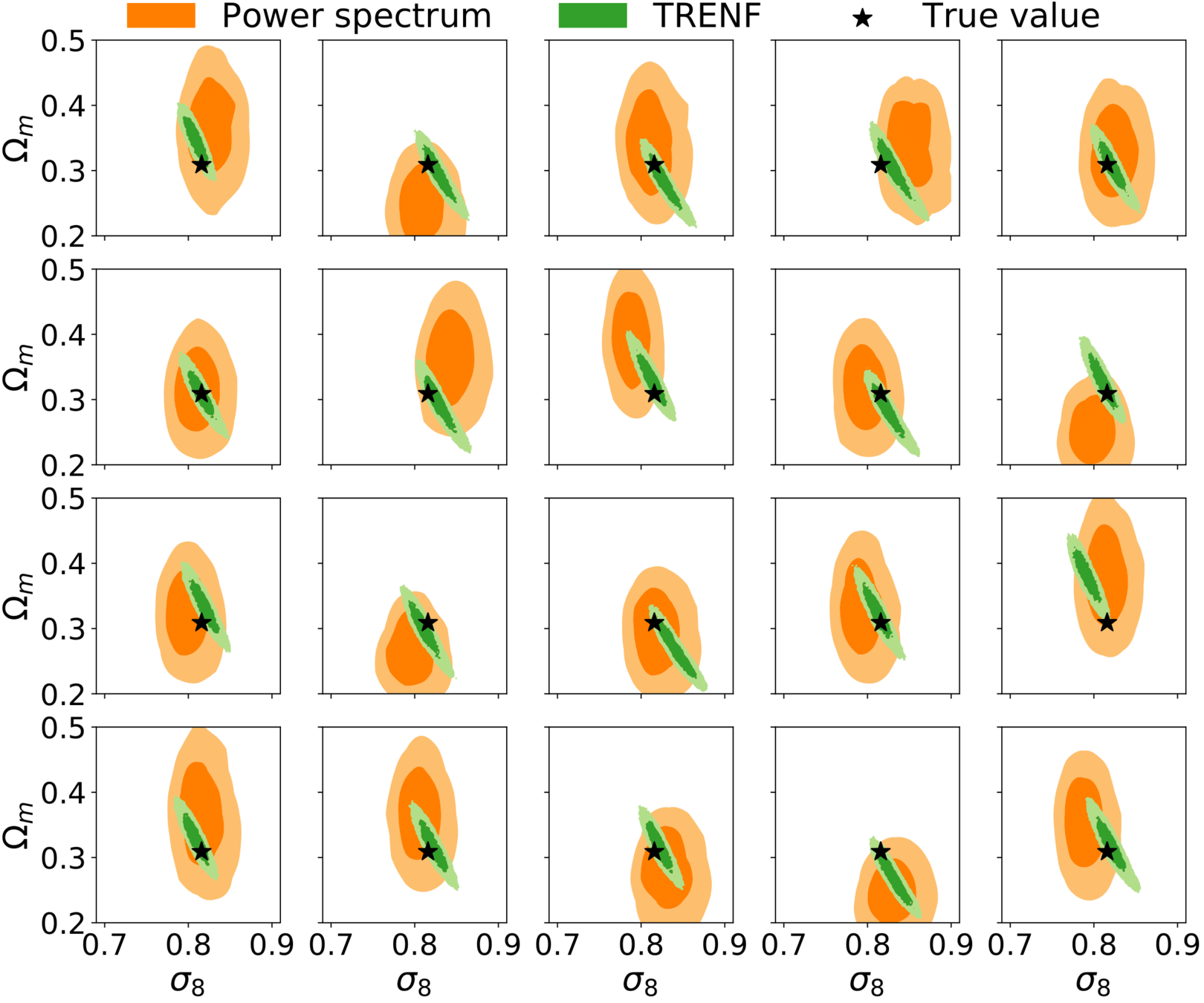
Normalising flows en cosmologia
Simulation-based Inference

arXiv:1911.01429

arxiv:2211.00723
Simulation-based Inference en cosmology

Las soluciones de ecuaciones diferenciales ordinarias (ODEs) son siempre invertibles!
Problemas NFs: Falta expresividad
- Function invertible
- Jacobiano tratable
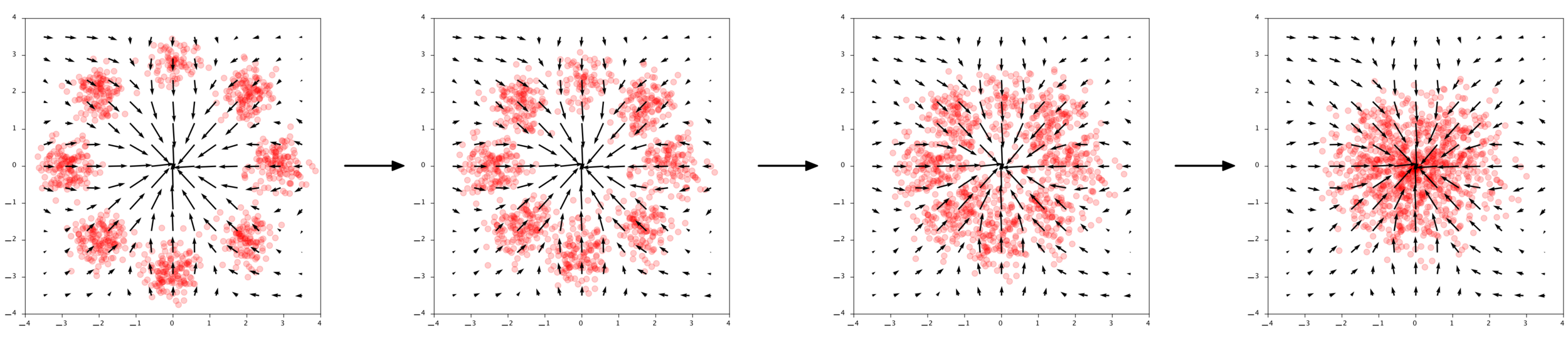
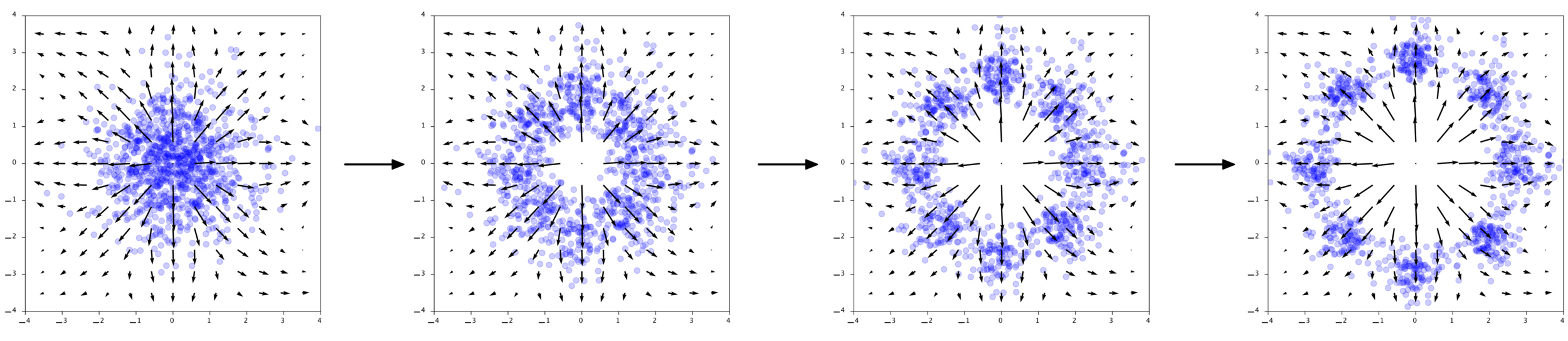
Chen et al. (2018), Grathwohl et al. (2018)
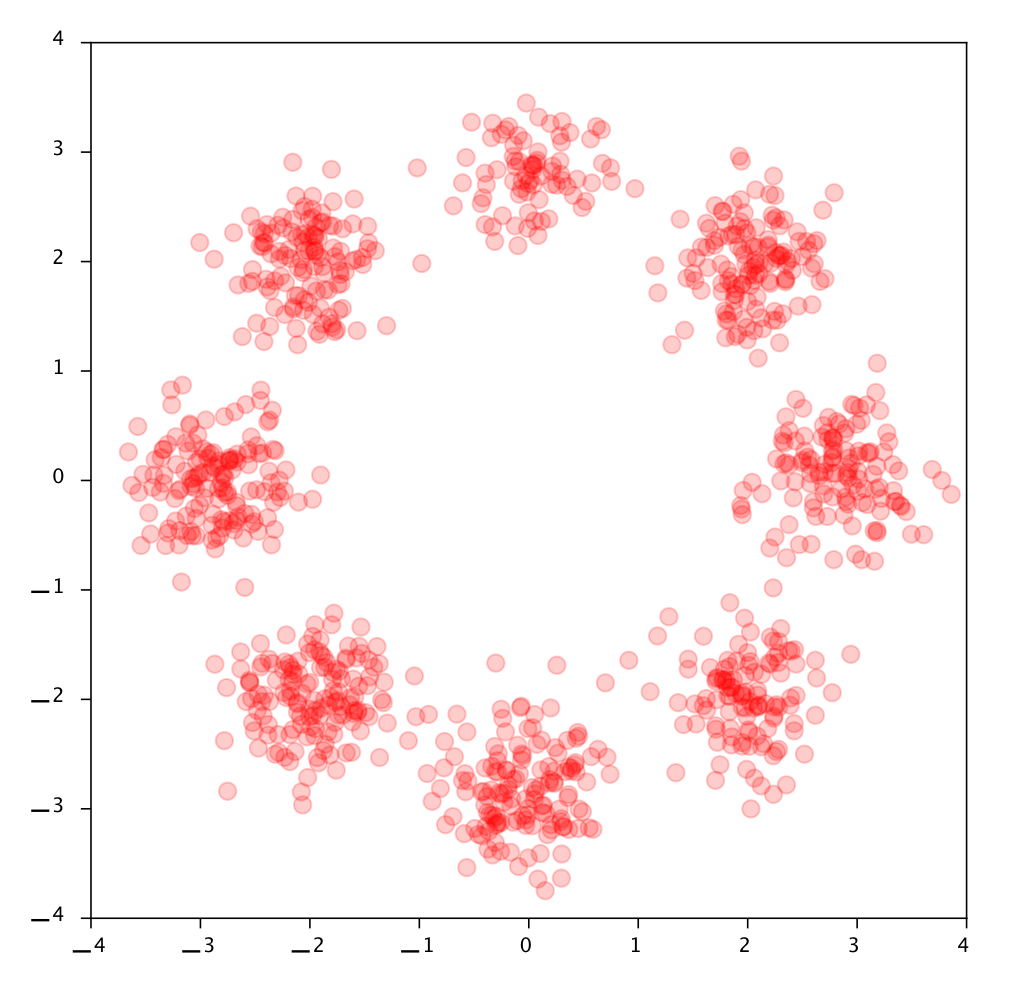
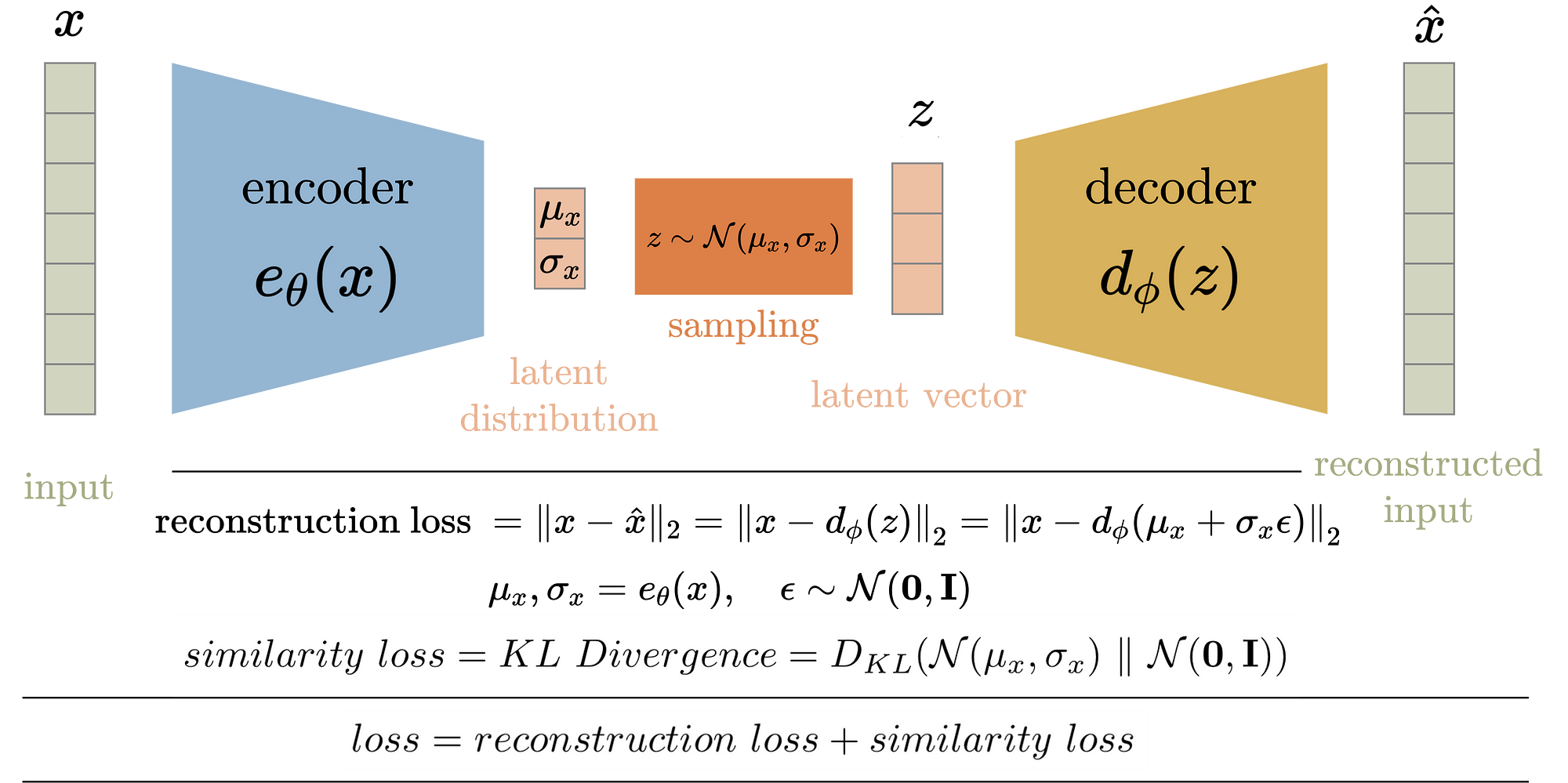
Variational Auto Encoders






Complex
Simple
Variational Auto Encoders




Maximizar el likelihood o algo que se le parezca: Variational Inference
No es simetrica!
La divergencia de Kullback-Leibler (KL):
Distancia entre dos distribuciones de probabilidad

Forward KL
Backward KL
Evidence Lower Bound
(ELBO)
Distancia al posterior real
Encontrar
1. ELBO es un lower bound del likelihood
2. Maximizar ELBO = Minimizar KL
Maximizar ELBO maximiza ev/likelihood
Maximizar ELBO para aproximar el posterior
Tutorial 1: Maximizar ELBO para aproximar posteriors en cosmologia


Variational Auto Encoders




Reconstruccion (MSE)
Regularizacion
- Continuo puntos cercanos en espacio latente deberian ser cercanos en el espacio de los datos
- Completo cualquier punto sampleado del espacio latente debe llevar a un ejemplo sensible de los datos


arxiv:2008.03833
Variational Auto Encoders en Astro
Tutorial 2: Generar galaxias con VAEs


Reverse diffusion: Quitar ruido al paso previo
Forward diffusion: Ruido Gaussian (fijo)



Una persona medio Yoda medio Gandalf
Diffusion models
+ dimensiones(z) = dimensiones(x)
+ encoder fijo: ruido gaussiano
Deep VAE
Diffusion =






Encoder
Ruido Gaussiano
Decoder
(neural network)
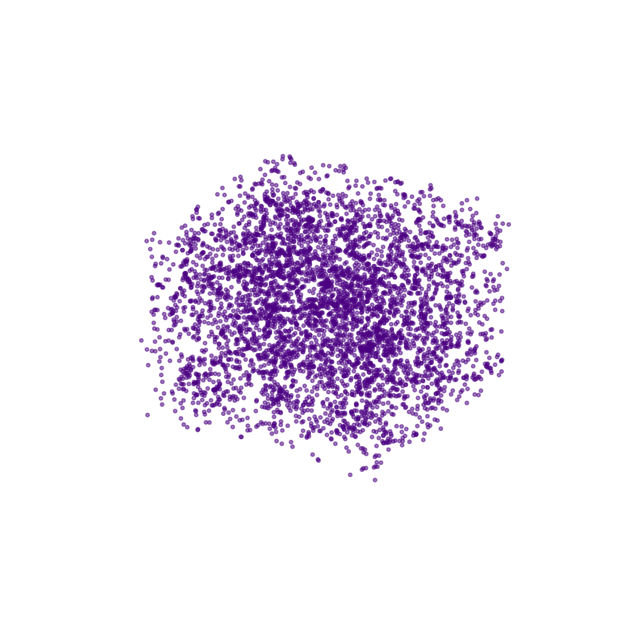
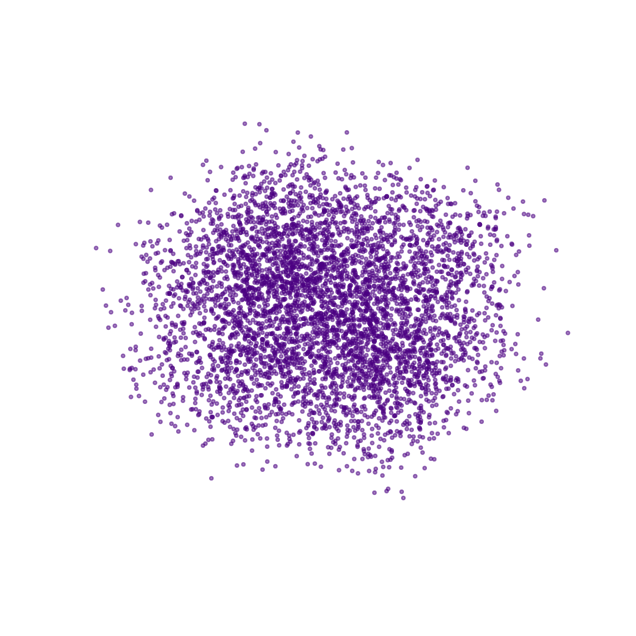
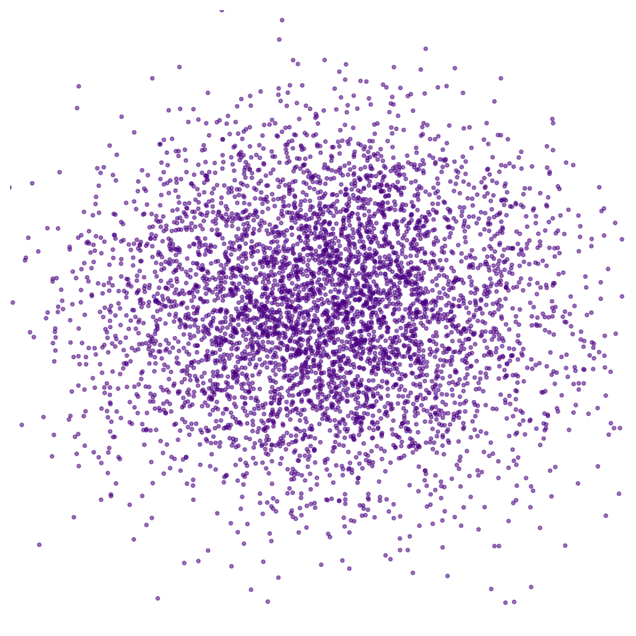

Cosmologia
Diffusion models en cosmologia
Reverse diffusion: Quitar ruido al paso previo
Forward diffusion: Ruido Gaussian (fijo)

arxiv:2104.13478
El zoo de arquitecturas:
déjate llevar por las simetrias
Propiedades de los nodos (posiciones, velocidades...)
Input
Propiedades galaxias ruidosas
Output
Prediccion del ruido
kNN (~20)
Graph neural networks para predecir el ruido
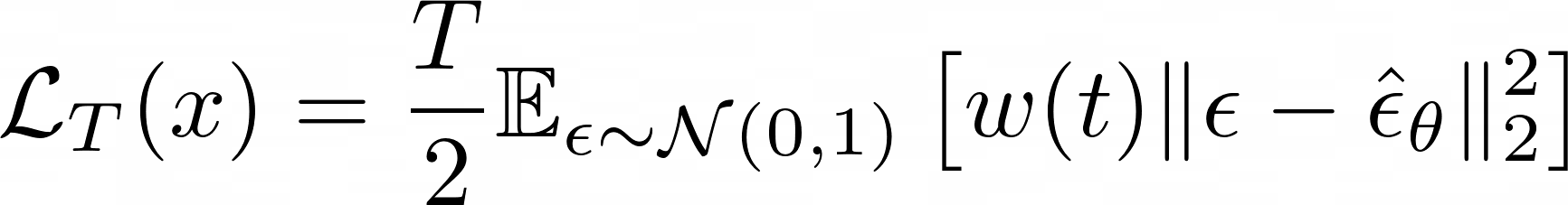
Prior
Diffusion
Reconstruction
Se un Bayesian de verdad: siempre maximiza el likelihood
arxiv:2107.00630
arxiv:2303.00848
Maximum Likelihood = Denoising
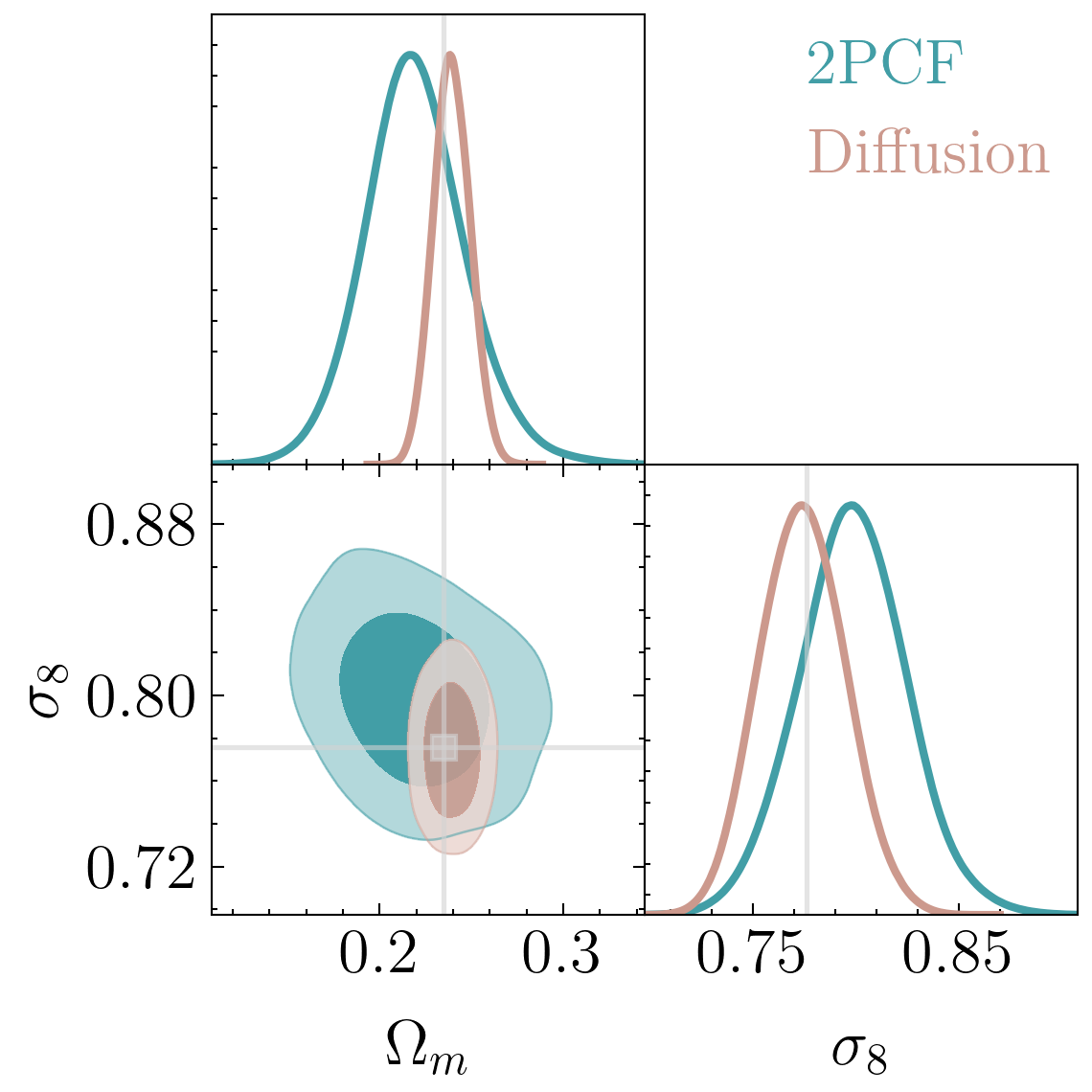
Tutorial 3: Generar jets de partículas con diffusion models

-
Books by Kevin P. Murphy
- Machine learning, a probabilistic perspective
- Probabilistic Machine Learning: advanced topics
- ML4Astro workshop https://ml4astro.github.io/icml2023/
- ProbAI summer school https://github.com/probabilisticai/probai-2023
- IAIFI Summer school
- Blogposts
cuestalz@mit.edu

Modelos Generativos Summer School Latam
By carol cuesta
Modelos Generativos Summer School Latam
- 1,122



