Carol Cuesta-Lazaro (IAIFI Fellow)
in collaboration with Siddarth Mishra-Sharma
Diffusion Models for Cosmology
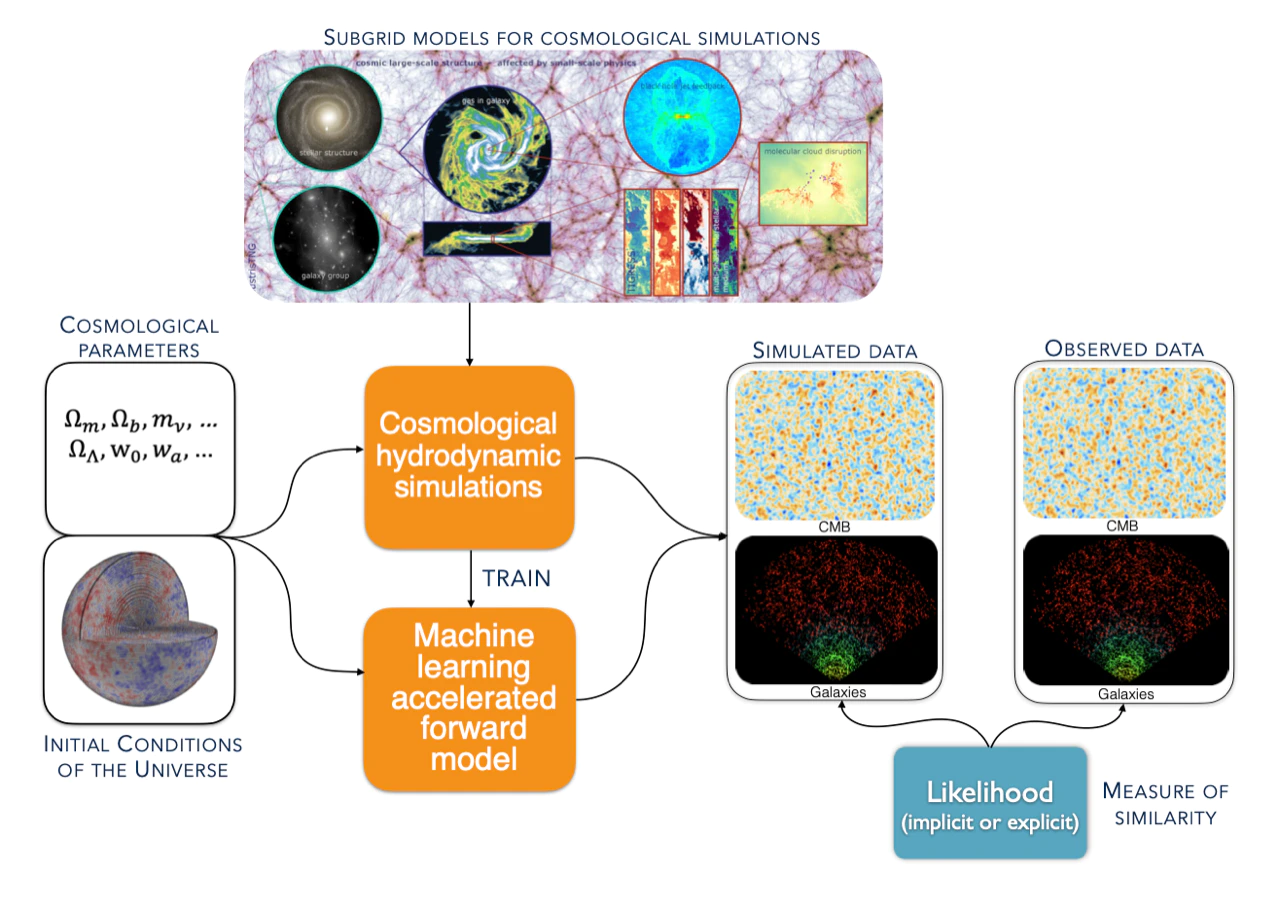
Initial Conditions of the Universe
Laws of gravity
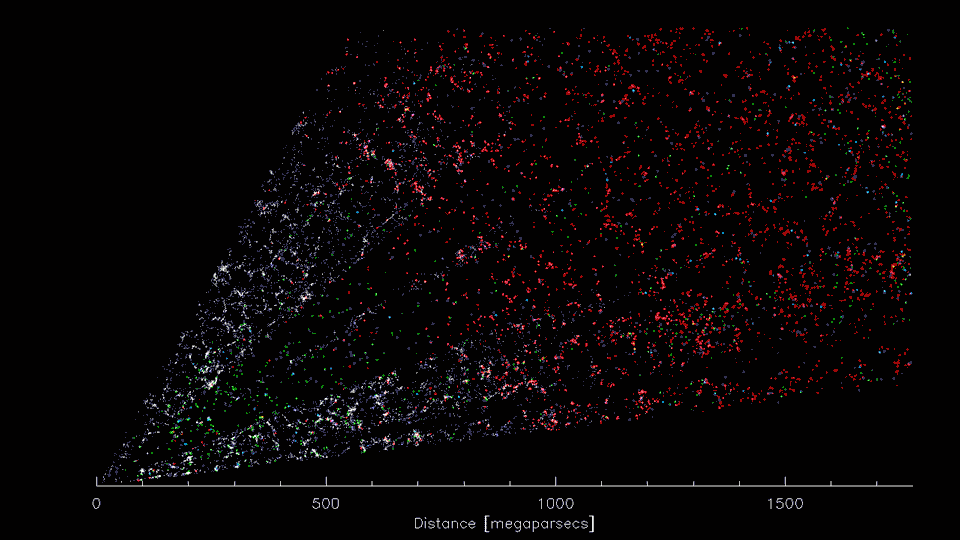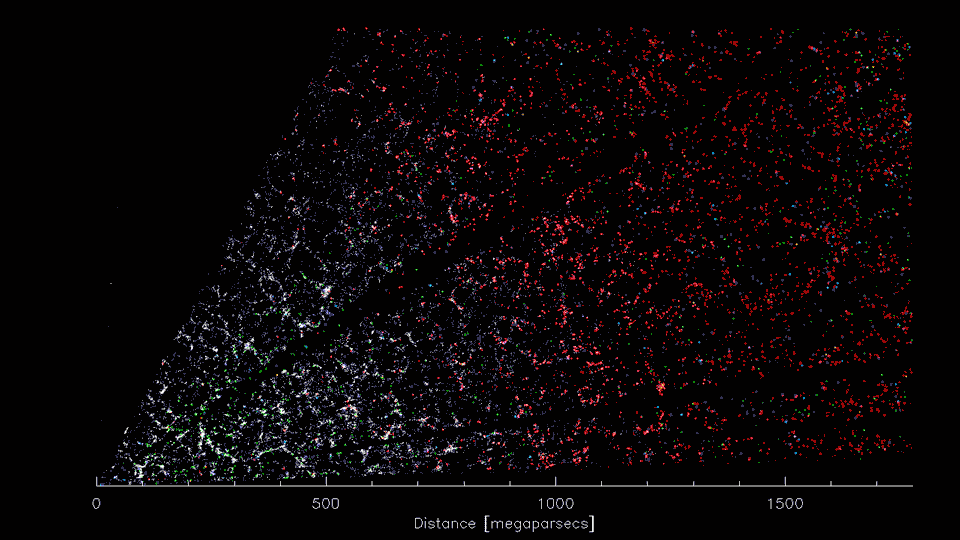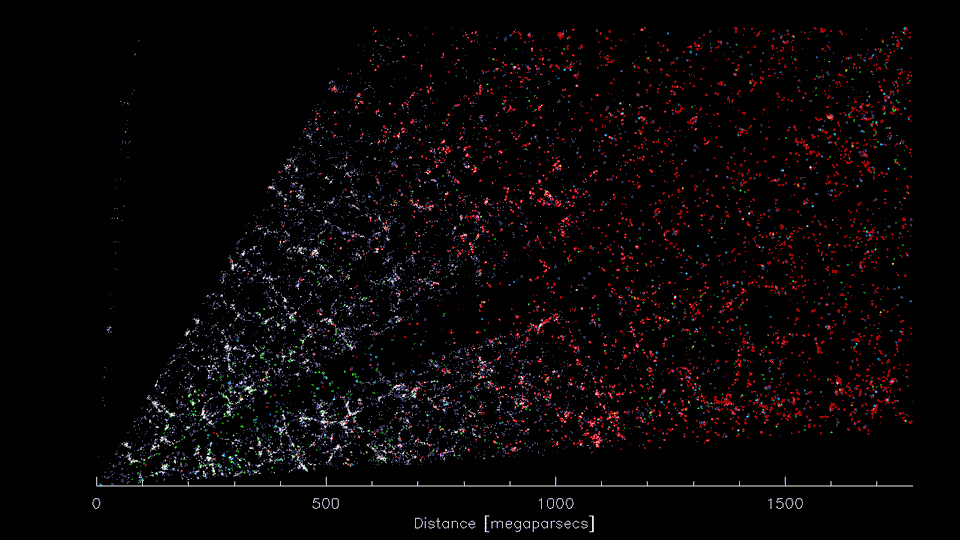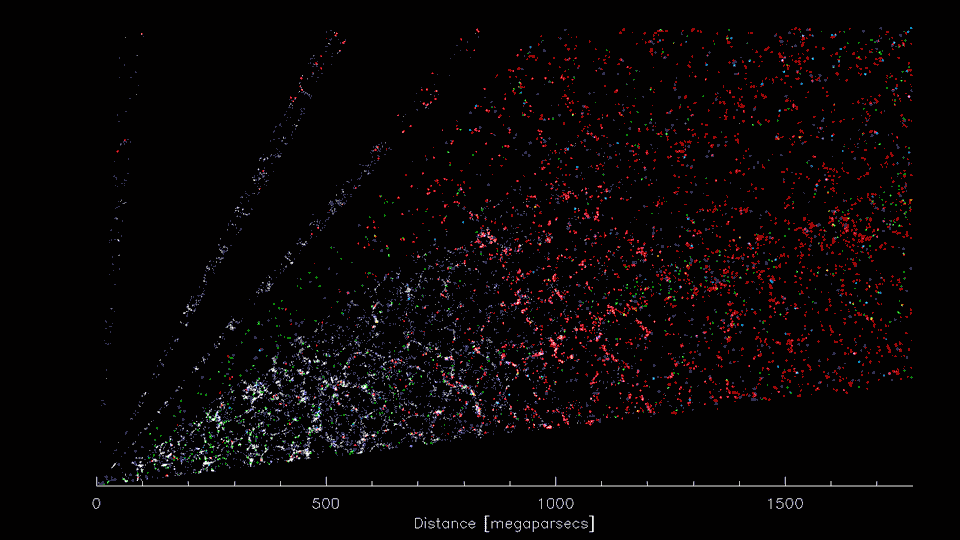
3-D distribution of galaxies
Which are the ICs of OUR Universe?
Primordial non-Gaussianity?
Probe Inflation
Galaxy formation
3-D distribution of dark matter
Is GR modified on large scales?
How do galaxies form?
Neutrino mass hierarchy?
ML for Large Scale Structure:
A wish list
Generative models
Learn p(x)
Evaluate the likelihood of a 3D map, as a function of the parameters of interest
1
Combine different galaxy properties (such as velocities and positions)
2
Sample 3D maps from the posterior distribution
3
p(
)
|
\mathrm{Cosmology}
Explicit Density
Implicit Density
Tractable Density
Approximate Density
Normalising flows
Variational Autoencoders
Diffusion models
Generative Adversarial Networks
The zoo of generative models
z_T
z_{0}
z_{1}
z_{2}
p_\theta(z_{t-1}|z_t)
q(z_t|z_{t-1})
Reverse diffusion: Denoise previous step
Forward diffusion: Add Gaussian noise (fixed)
Diffusion models
A person half Yoda half Gandalf
z_T
z_{0}
z_{1}
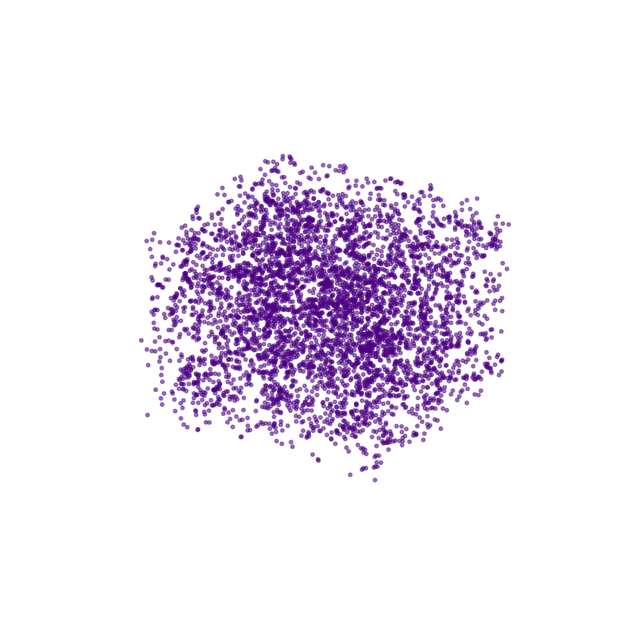
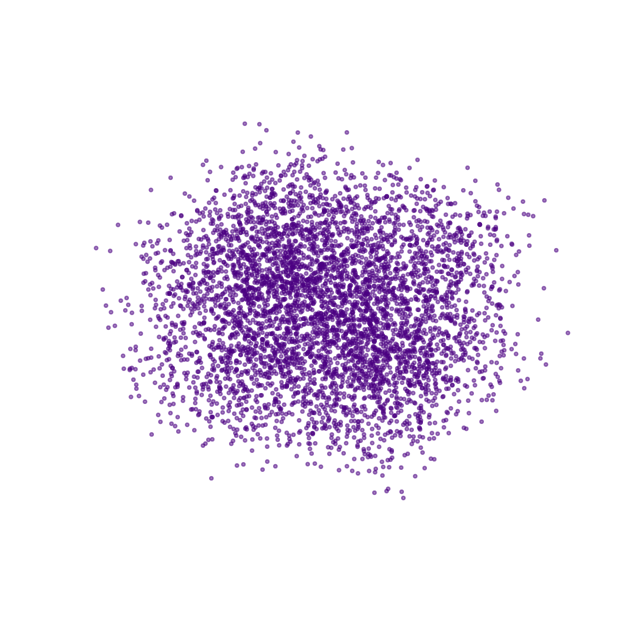
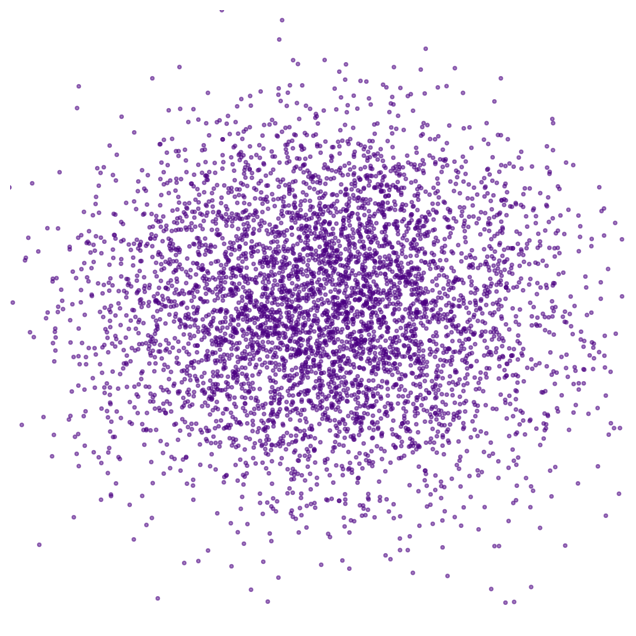
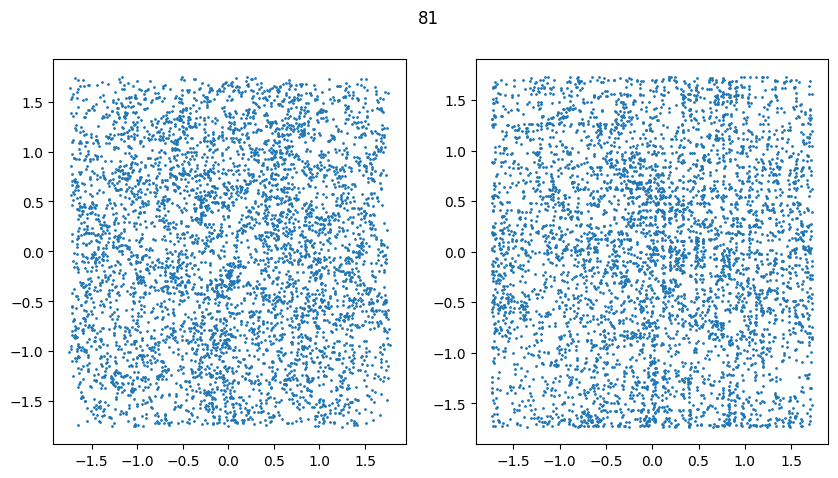
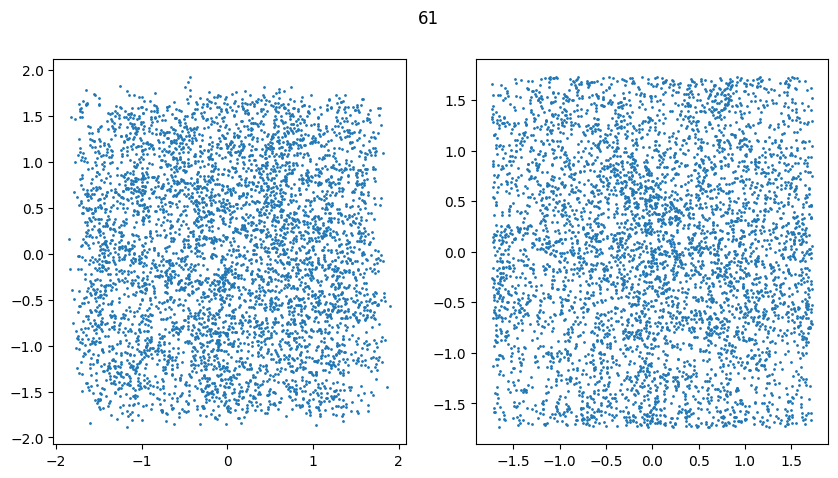
Diffusion on 3D coordinates
z_{2}
p_\theta(z_{t-1}|z_t)
q(z_t|z_{t-1})
Reverse diffusion: Denoise previous step
Forward diffusion: Add Gaussian noise (fixed)
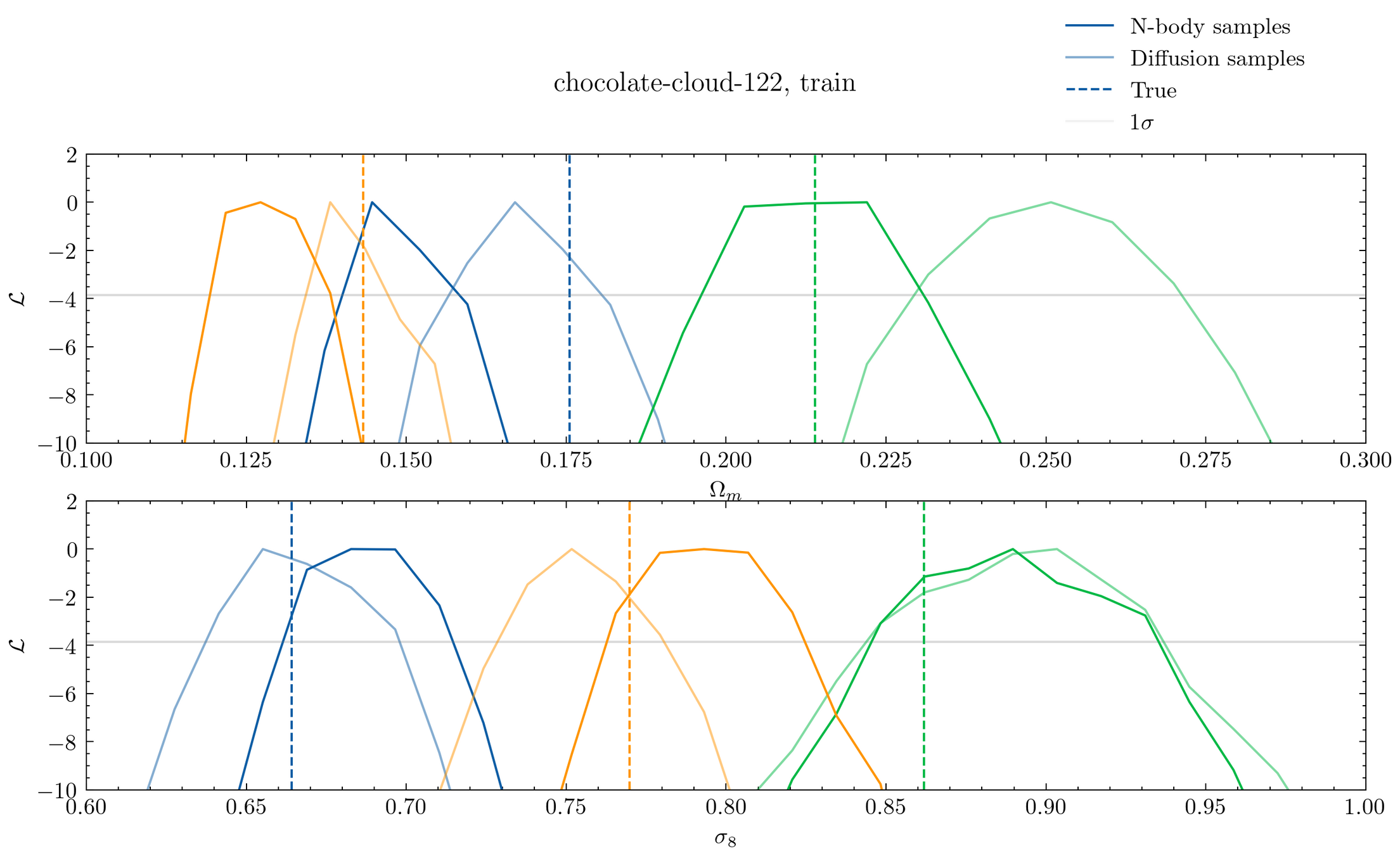
Cosmology
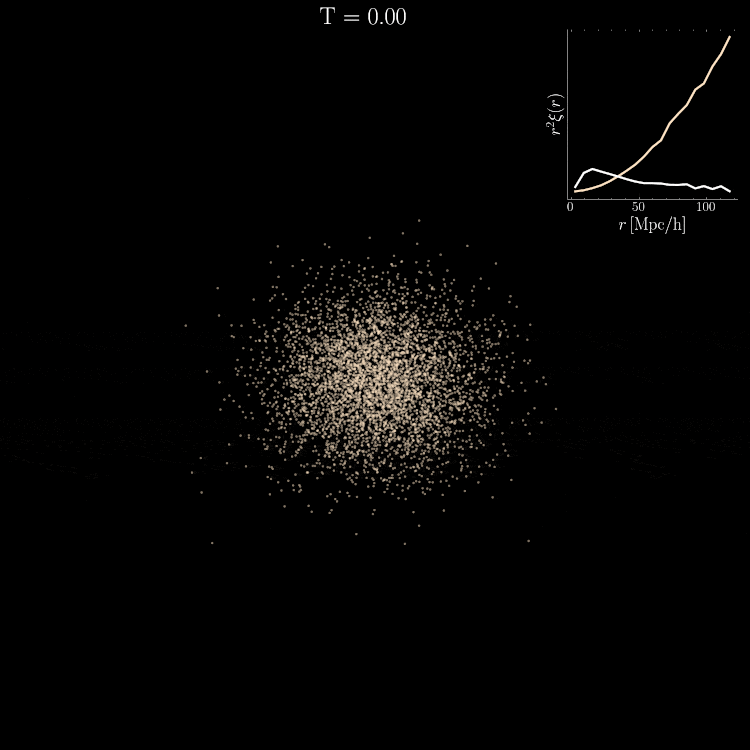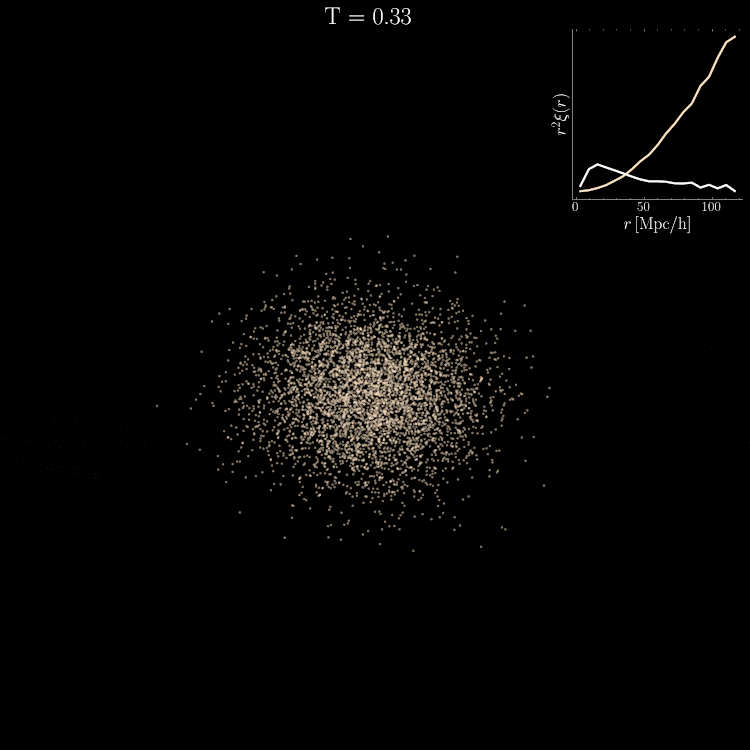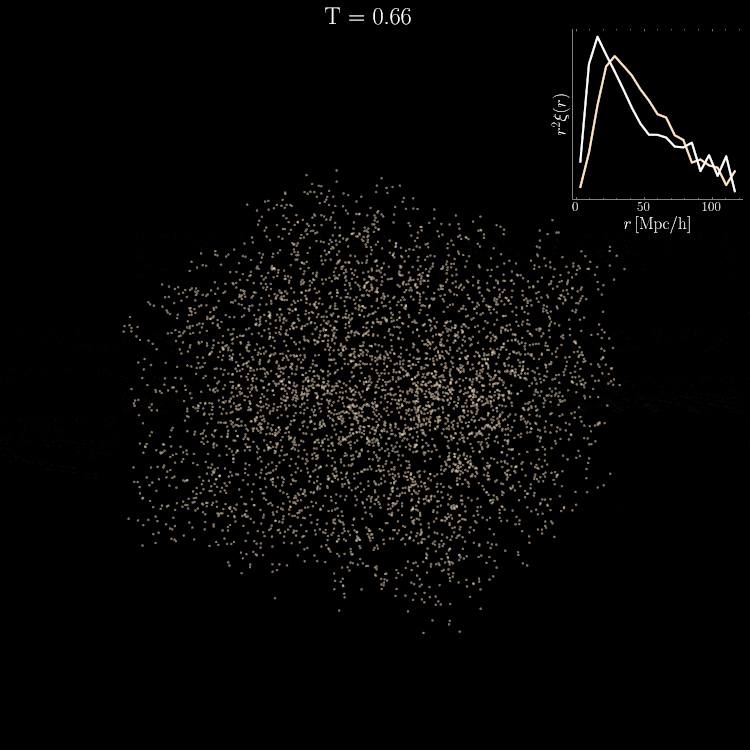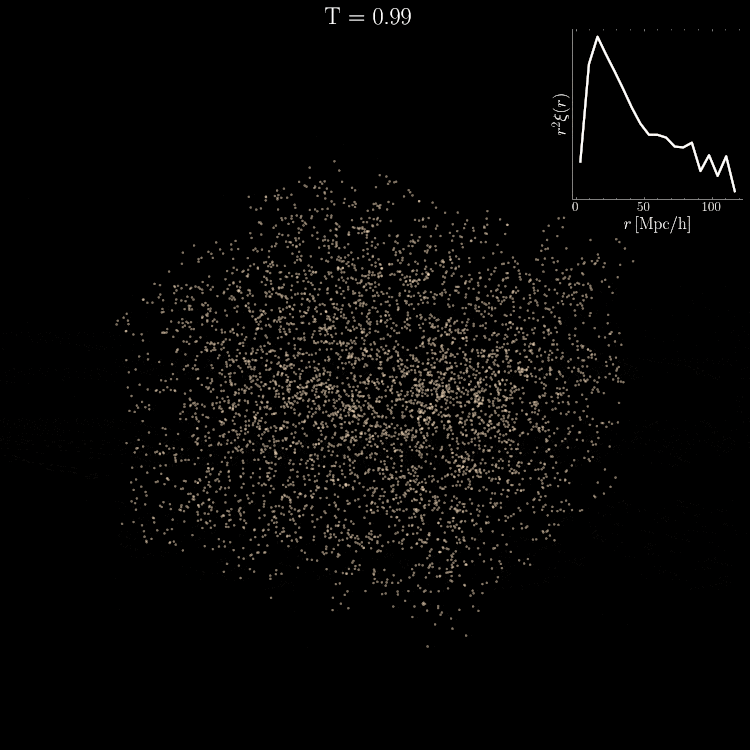
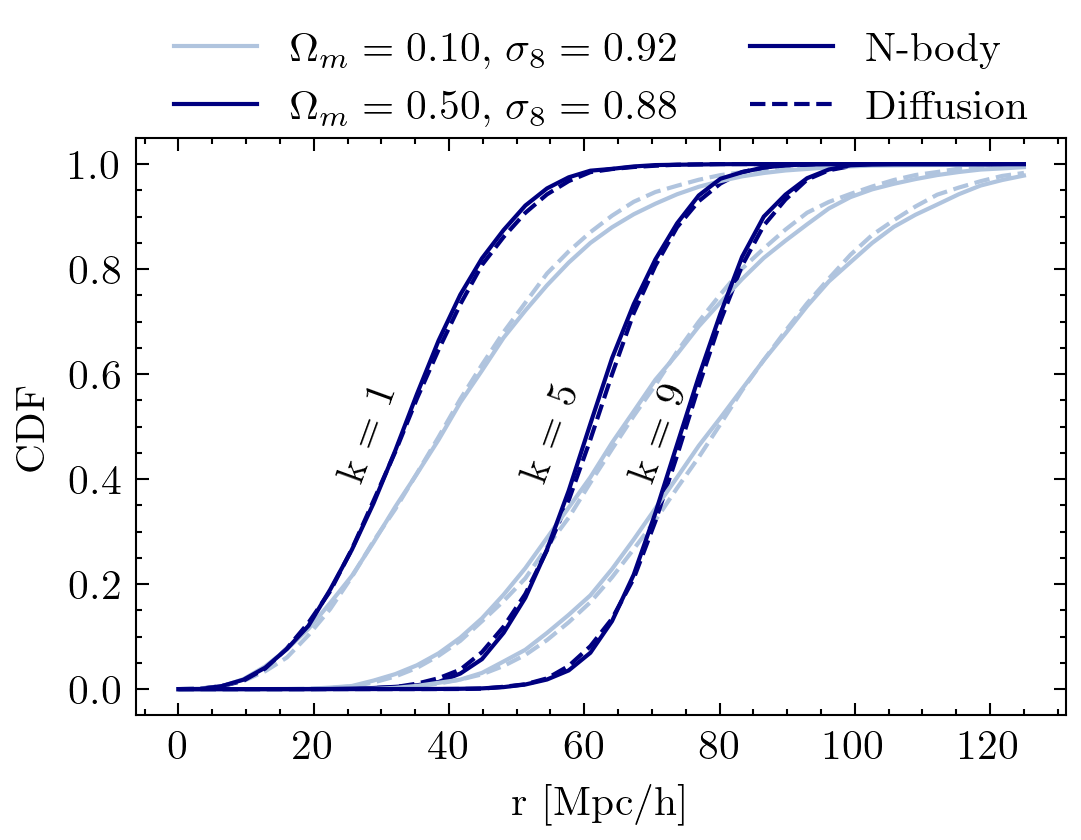
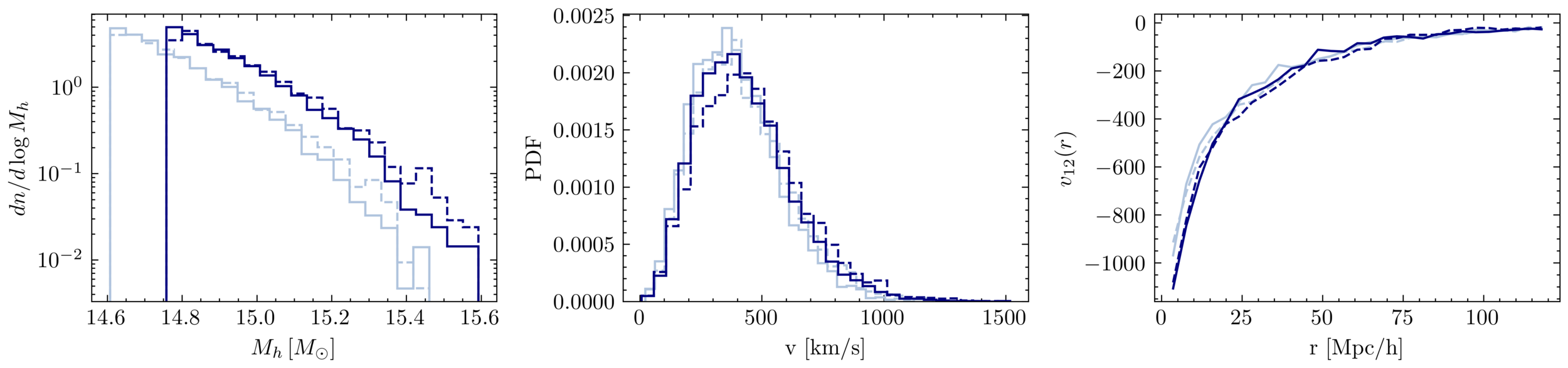
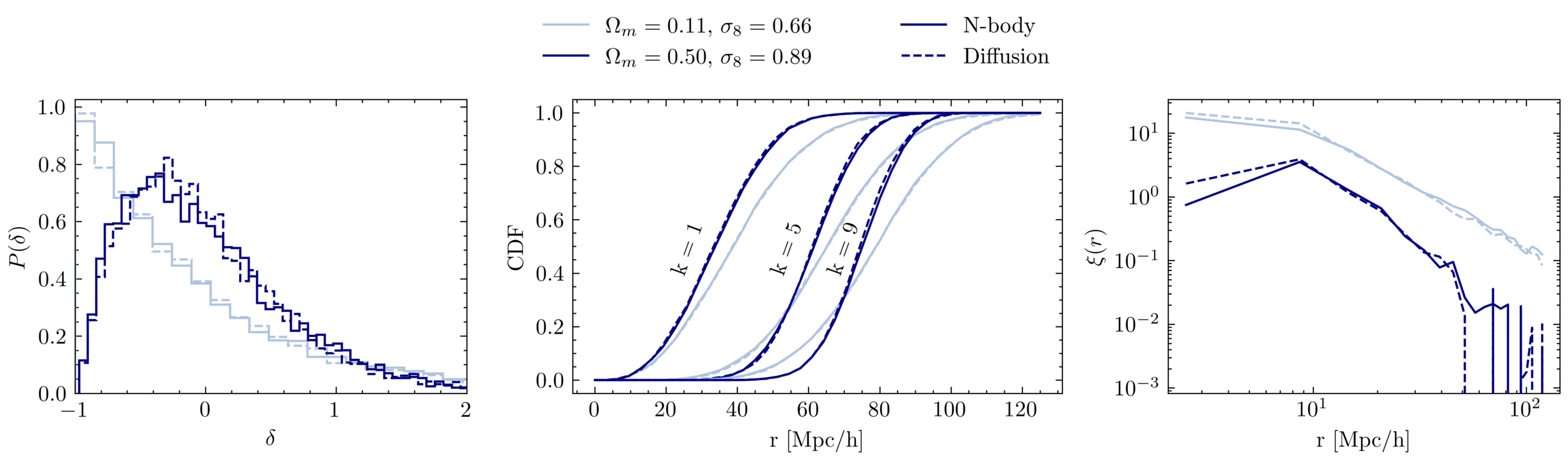
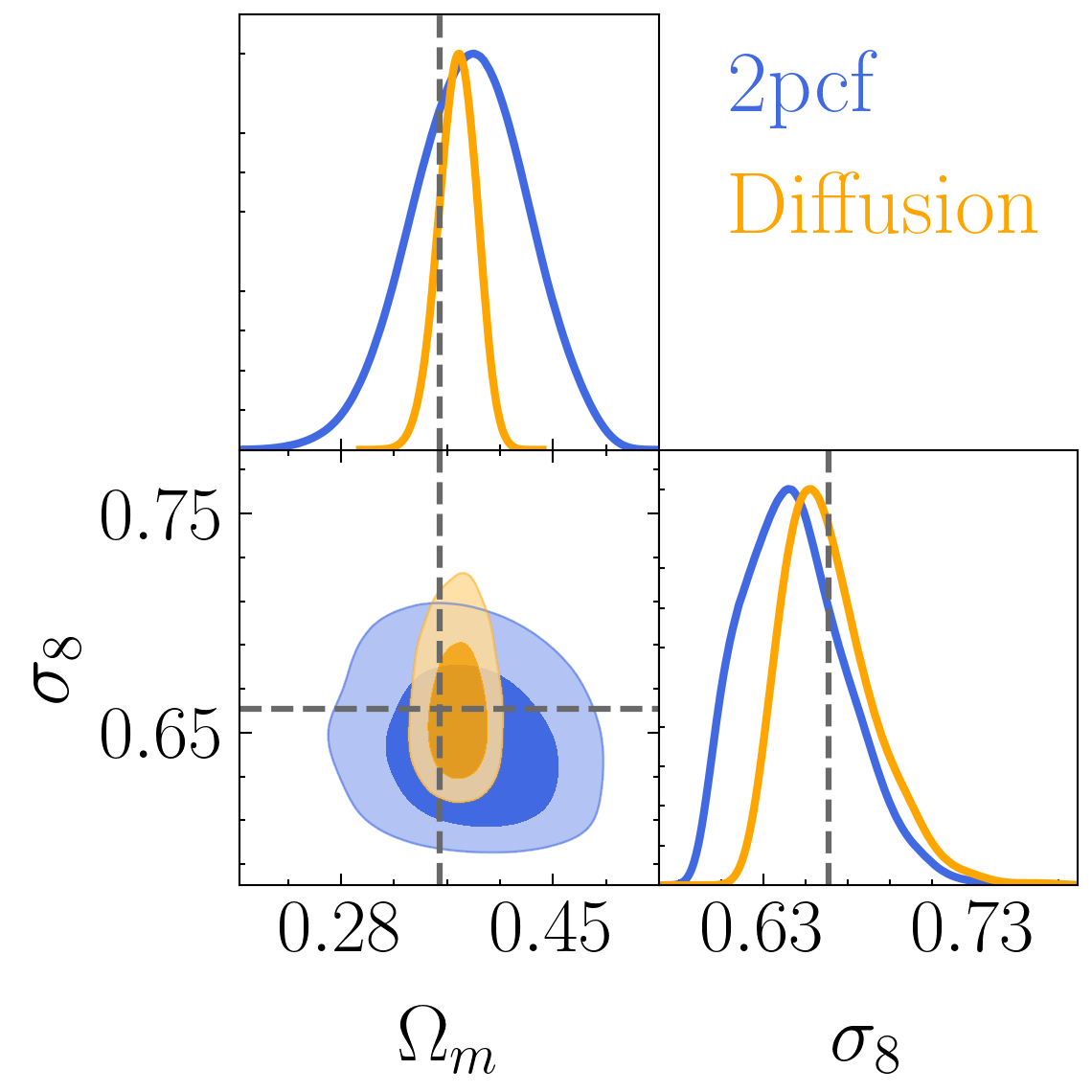
Setting tight constraints with only 5000 halos
h_0
h_1
h_5
h_4
h_2
h_3
h_6
e_{01}
e_{12}
Node features
Edge features
\mathcal{G} = h^{L}_i, e^{L}_{ij} \rightarrow h^{L+1}_i, e^{L+1}_{ij}
e^{L+1}_{ij} = \phi_e(e^L_{ij}, h^L_i, h^L_j)
edge embedding
h^{L+1}_{i} = \phi_h( h^L_i, \mathcal{A}_j e^{L+1}_{ij})
node embedding
Input
noisy halo properties
Output
noise prediction
A variational Lower Bound
p(Z|X) = \frac{p(X|Z)p(Z)}{p(X)}
q(Z) \approx p(Z|X)
Inference is hard....
known PDF with some free parameters
Kullback-Leibler divergence
distance between two distributions
D_\mathrm{KL}(p(x)||q(x)) = \int p(x) \ln \frac{p(x)}{q(x)} dx
Not symmetric!
D_\mathrm{KL}(p(x)||q(x)) \geq 0
D_\mathrm{KL}(p(x)||q(x)) = 0 \Leftrightarrow p = q
A variational Lower Bound
\begin{aligned}
& KL\left[q(Z) \| p(Z|X)\right] = \\
&= \int_Z q(Z) \log \frac{q(Z)}{p(Z|X)} \\
\end{aligned}
\begin{aligned}
& KL\left[q(Z) \| p(Z|X)\right] = \\
&= \int_Z q(Z) \log \frac{q(Z)}{p(Z|X)} \\
&= -\int_Z q(Z) \log \frac{p(Z|X)}{q(Z)} \\
&= - \left(\int_Z q(Z) \log \frac{p(X,Z)}{q(Z)} - \int_Z q(Z) \log p(X)\right) \\
&= -\int_Z q(Z) \log \frac{p(X,Z)}{q(Z)} + \log p(X) \int_Z q(Z) \\
&= -\mathrm{VLB} + \log p(X)
\end{aligned}
\begin{aligned}
& KL\left[q(Z) \| p(Z|X)\right] = \\
&= \int_Z q(Z) \log \frac{q(Z)}{p(Z|X)} \\
&= -\int_Z q(Z) \log \frac{p(Z|X)}{q(Z)} \\
&= - \left(\int_Z q(Z) \log \frac{p(X,Z)}{q(Z)} - \int_Z q(Z) \log p(X)\right) \\
\end{aligned}
p(Z|X) = \frac{p(X|Z)p(Z)}{p(X)}
Inference = Optimisation
q(Z) \approx p(Z|X)
\mathrm{VLB} = \log p(X) - KL\left[q(Z) \| p(Z|X)\right]
\mathrm{VLB} \leq \log p(X)
\mathrm{VLB} = \log p(X)
only if q perfectly describes p!
\log p(X)
\mathrm{VLB} = \log E_{q(z)} \frac{p(X,Z)}{q(Z)}
KL\left[q(Z) \| p(Z|X)\right]
- \log p(x) \leq -\mathrm{VLB}(x) =
\gray{\mathrm{Prior Loss}} + \blue{\mathrm{Diffusion Loss}}
\gray{\mathrm{Prior Loss} = \mathrm{KL}(q(z_T|x)|p(z_T))}
\blue{\mathrm{Diffusion Loss} = }
\blue{\sum_{t} D_\mathrm{KL} \left[ q(z_{t-1}|z_{t},x) || p_\theta (z_{t-1}|z_{t}) \right]}
Ensure consistency forward/reverse
Challenge Learning a well calibrated likelihood from only 2000 N-body simulations
All learnable functions
Equivariant functions
Data constraints
Credit: Adapted from Tess Smidt
Equivariant diffusion
Implications for robustness and interpretability?
+ Galaxy formation
+ Observational systematics (Cut-sky, Fiber collisions)
+ Lightcone, Redshift Space Distortions....
Forward Model
N-body simulations
Observations
SIMBIG arXiv:2211.00723
Copy of deck
By carol cuesta
