Generative Models in Astrophysics
Carol Cuesta-Lazaro
IAIFI Fellow - Yale Data Science Seminar
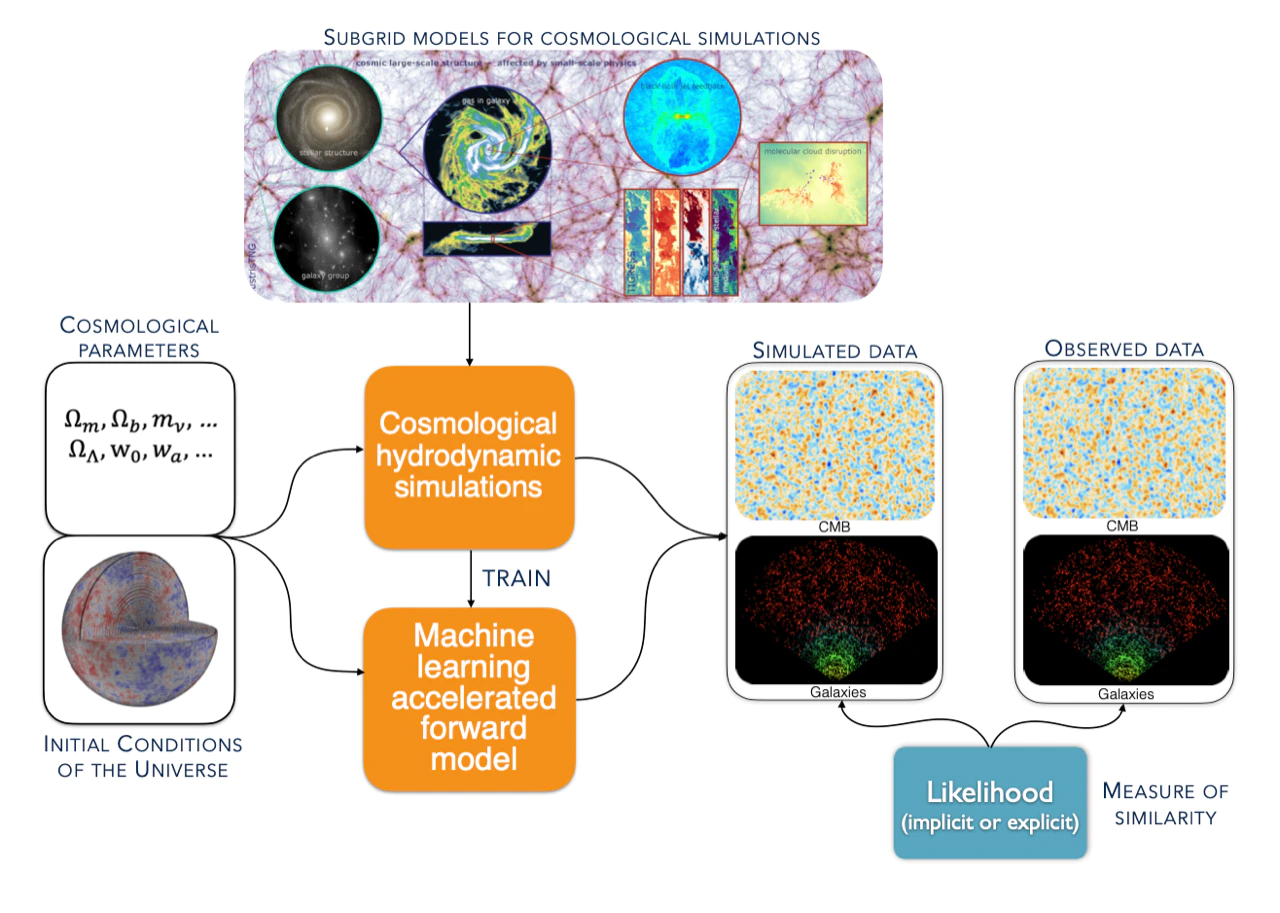
Initial Conditions of the Universe
Laws of gravity
3-D distribution of galaxies
Which are the ICs of OUR Universe?
Primordial non-Gaussianity?
Probe Inflation
Galaxy formation
3-D distribution of dark matter
Is GR modified on large scales?
How do galaxies form?
Neutrino mass hierarchy?
Dall-E 3
A 2D animation of a folk music band composed of anthropomorphic autumn leaves, each playing traditional bluegrass instruments, amidst a rustic forest setting dappled with the soft light of a harvest moon
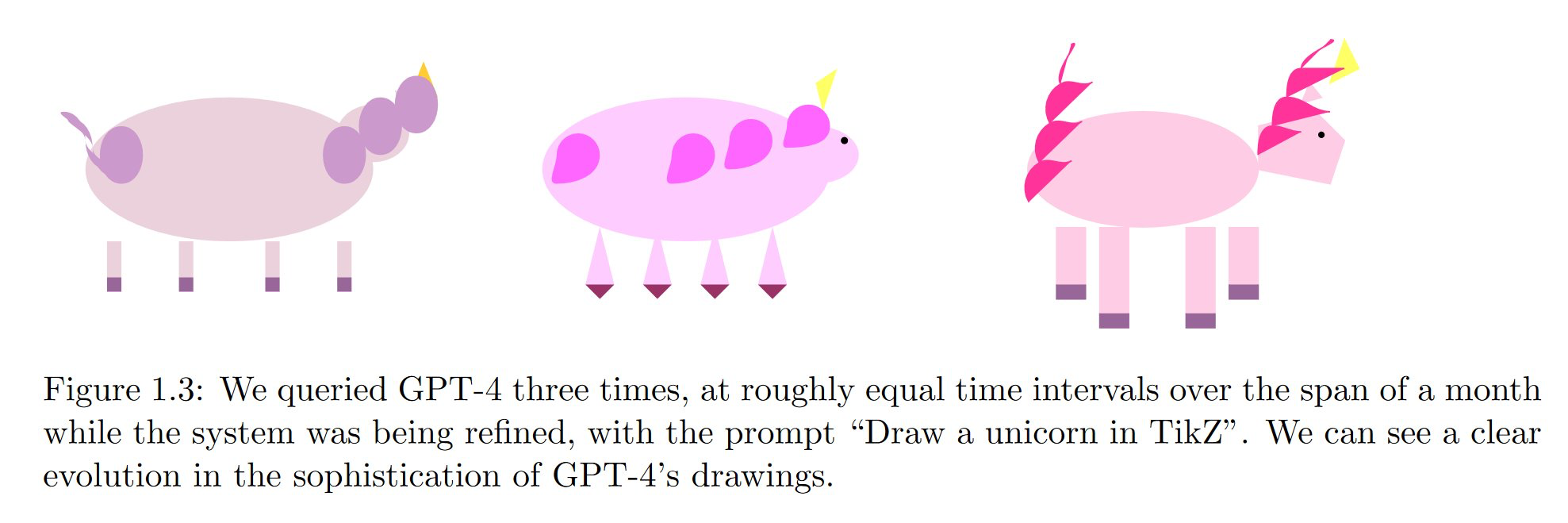
"Sparks of Artificial General Intelligence: Early experiments with GPT-4" Bubeck et al
Produce Javascript code that creates a random graphical image that looks like a painting of Kandinsky
Draw a unicorn in TikZ
ChatGPT
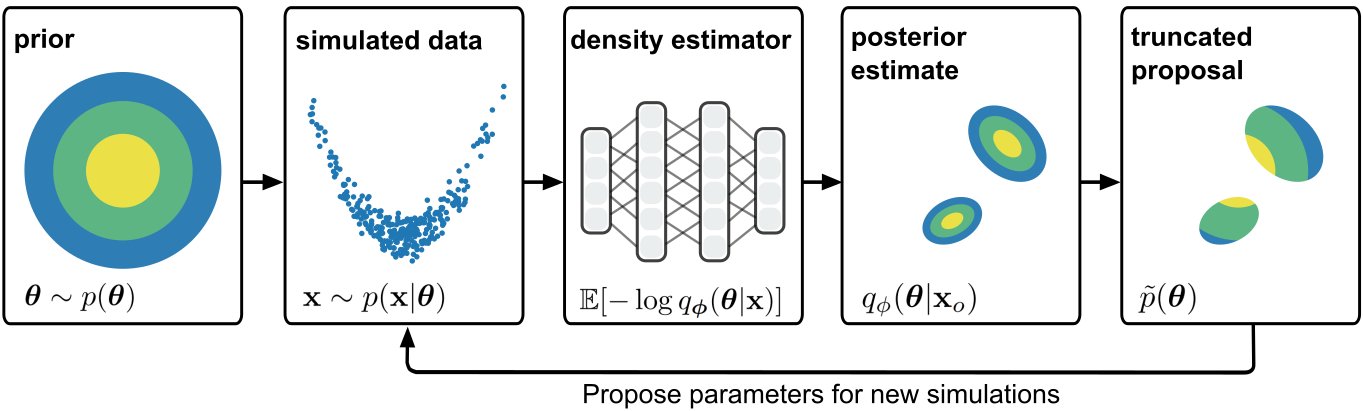
Emulation
x∼p(x∣y)
x \sim p(x|y)
Model uncertainties
Likelihood estimation
p(θ∣xobs)
p(\theta|x_\mathrm{obs})
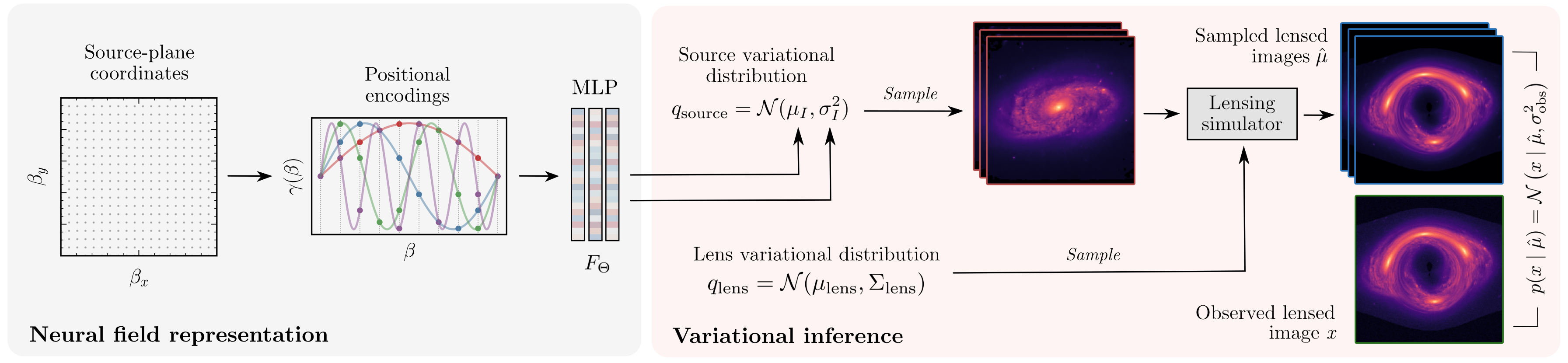
Complex priors
lensing
arxiv:2206.14820
pϕ(x)
p_\phi(x)
Data
A parametric PDF
Maximise the likelihood
(or something similar)
Explicit Density
Implicit Density
Tractable Density
Approximate Density
Normalising flows
Variational Autoencoders
Diffusion models
Generative Adversarial Networks
The zoo of generative models
The backbone of vision generative models
Reverse diffusion: Denoise previous step
Forward diffusion: Add Gaussian noise (fixed)
A person half Yoda half Gandalf
Diffusion Models
zT
z_T
z0
z_{0}
z1
z_{1}
z2
z_{2}
qθ(zt−1∣zt)
q_\theta(z_{t-1}|z_t)
p(zt∣zt−1)
p(z_t|z_{t-1})
Reverse diffusion: Denoise previous step
Forward diffusion: Add Gaussian noise (fixed)
Cosmology
Diffusion on point clouds
"Diffusion generative modeling for galaxy surveys: emulating clustering for inference at the field level" Carolina Cuesta-Lazaro, Siddarth Mishra-Sharma
Modelling galaxy surveys
p(x,y,z,vx,vy,vz,Mh∣Ωm,σ8)
p(x,y,z, v_x, v_y, v_z, M_h|\Omega_m, \sigma_8)
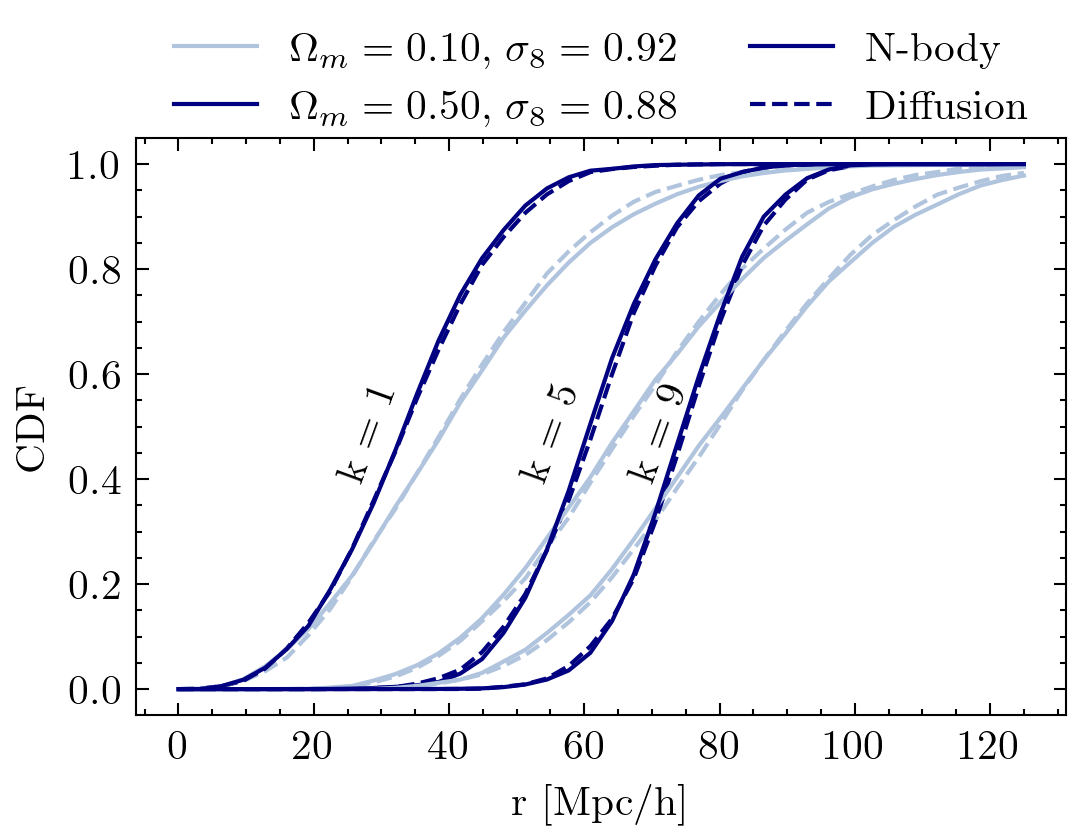
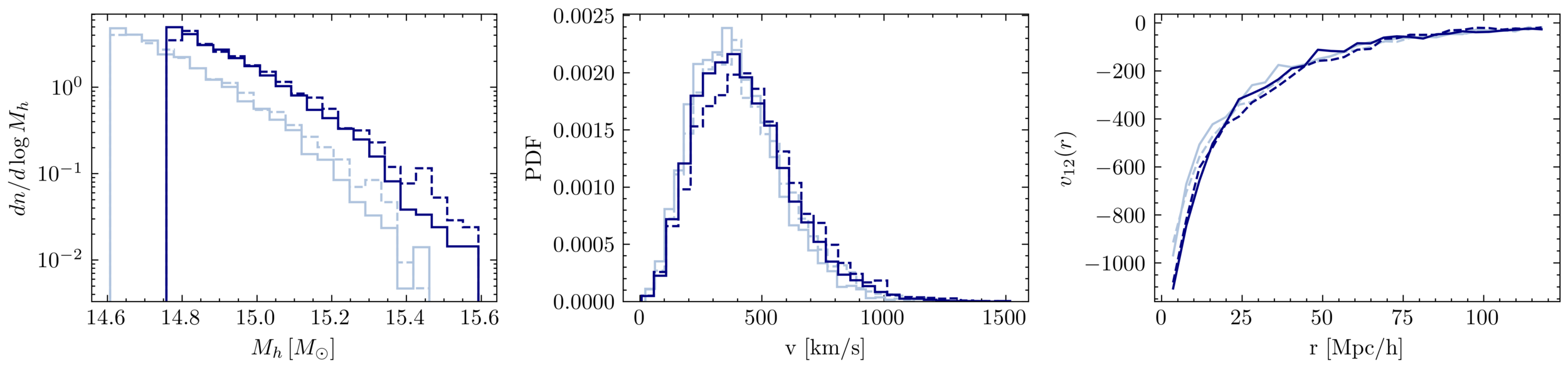
Halo Mass Function
Velocity
Mean pairwise velocity
h0
h_0
h1
h_1
h5
h_5
h4
h_4
h2
h_2
h3
h_3
h6
h_6
e01
e_{01}
e12
e_{12}
Node features
Edge features
G=hiL,eijL→hiL+1,eijL+1
\mathcal{G} = h^{L}_i, e^{L}_{ij} \rightarrow h^{L+1}_i, e^{L+1}_{ij}
eijL+1=ϕe(eijL,hiL,hjL)
e^{L+1}_{ij} = \phi_e(e^L_{ij}, h^L_i, h^L_j)
edge embedding
hiL+1=ϕh(hiL,AjeijL+1)
h^{L+1}_{i} = \phi_h( h^L_i, \mathcal{A}_j e^{L+1}_{ij})
node embedding
Input
noisy halo properties
Output
noise prediction
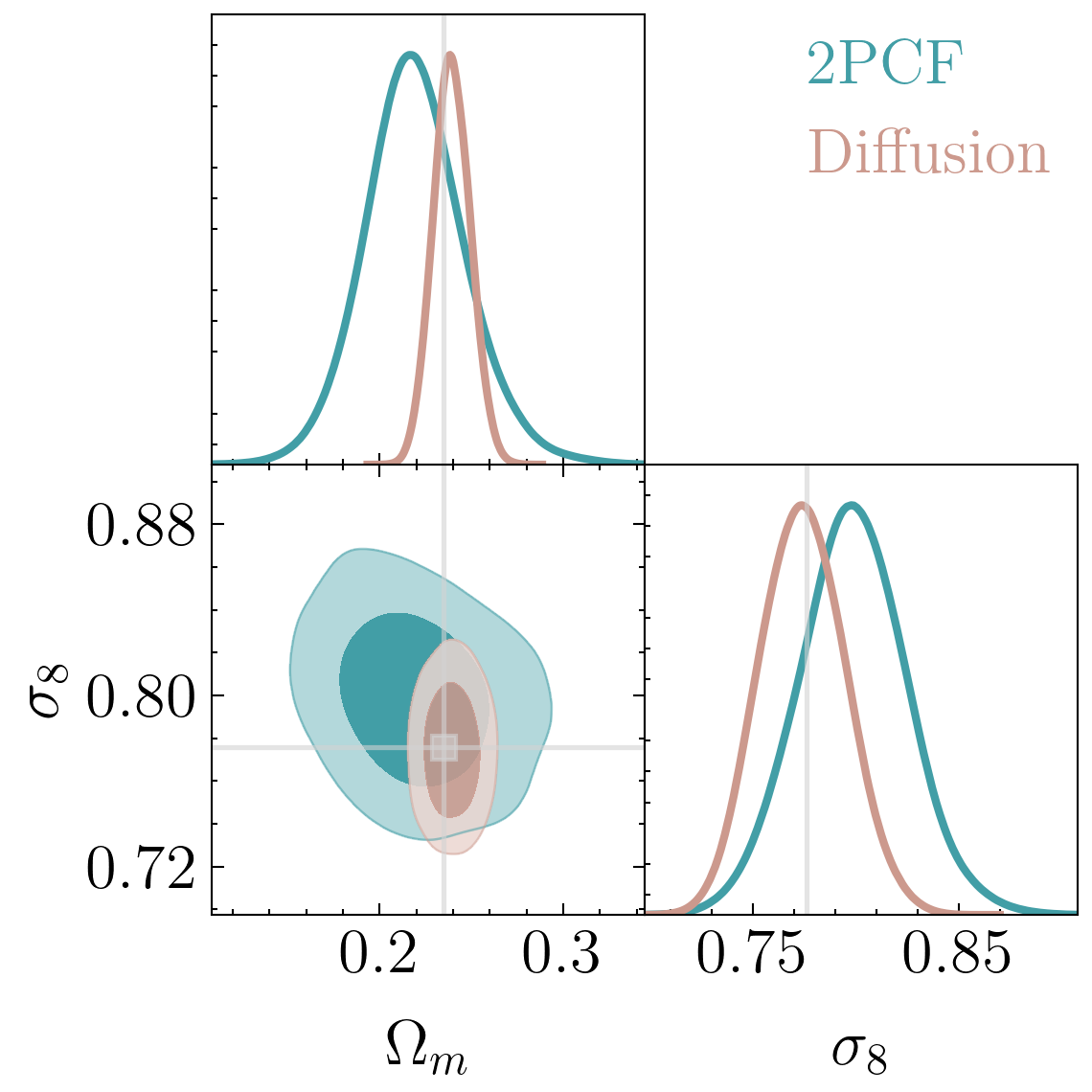
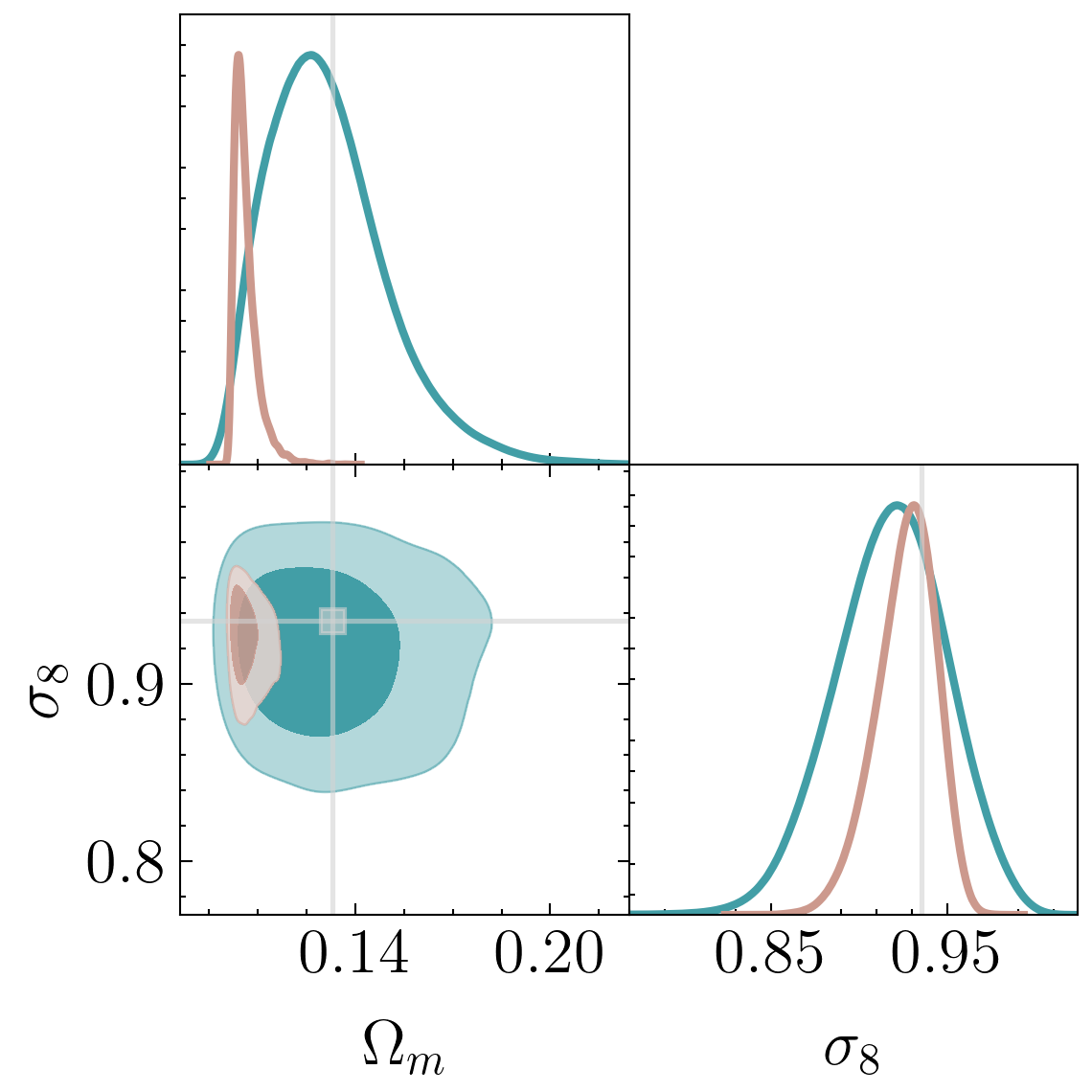
Tight constraints with only 5000 positions!
LT(x)=∑i=1TEq(zi∣x)DKL[q(zi−1∣zi,x)∣∣pθ(zi−1∣zi)]
\mathcal{L}_T(x) = \sum_{i=1}^T \mathbb{E}_{q(z_{i}|x)} D_{KL} \left[q(z_{i-1} | z_{i}, x) || p_\theta(z_{i-1} | z_{i}) \right]
−logp(x)≤−VLB(x)
-\log p(x) \leq -\mathrm{VLB}(x)
DKL(q(zT∣x)∣∣p(zT))+Eq(z0∣x)[−logp(x∣z0)]+LT(x)
D_{KL}(q(z_T|x) || p(z_T)) + \mathbb{E}_{q(z_0|x)} \left[-\log p(x|z_0) \right] + \mathcal{L}_T(x)
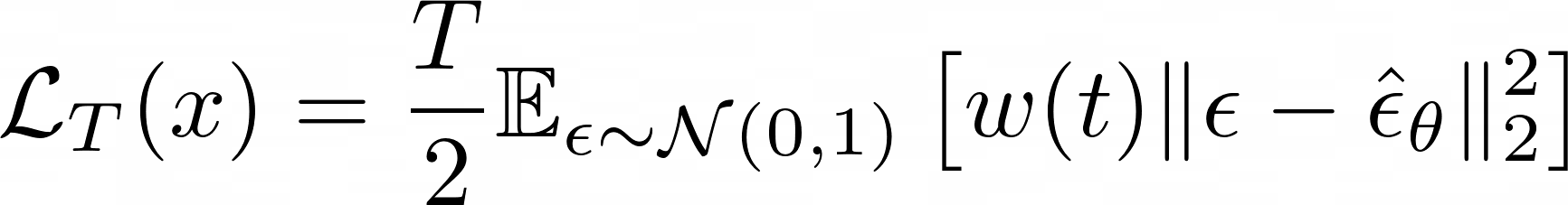
Prior loss
Diffusion loss
Reconstruction loss
Be a true Bayesian: Always maximise the likelihood
arxiv:2107.00630
arxiv:2303.00848
Maximum Likelihood = Denoising
25h−1Mpc
25 \, h^{-1}\mathrm{Mpc}
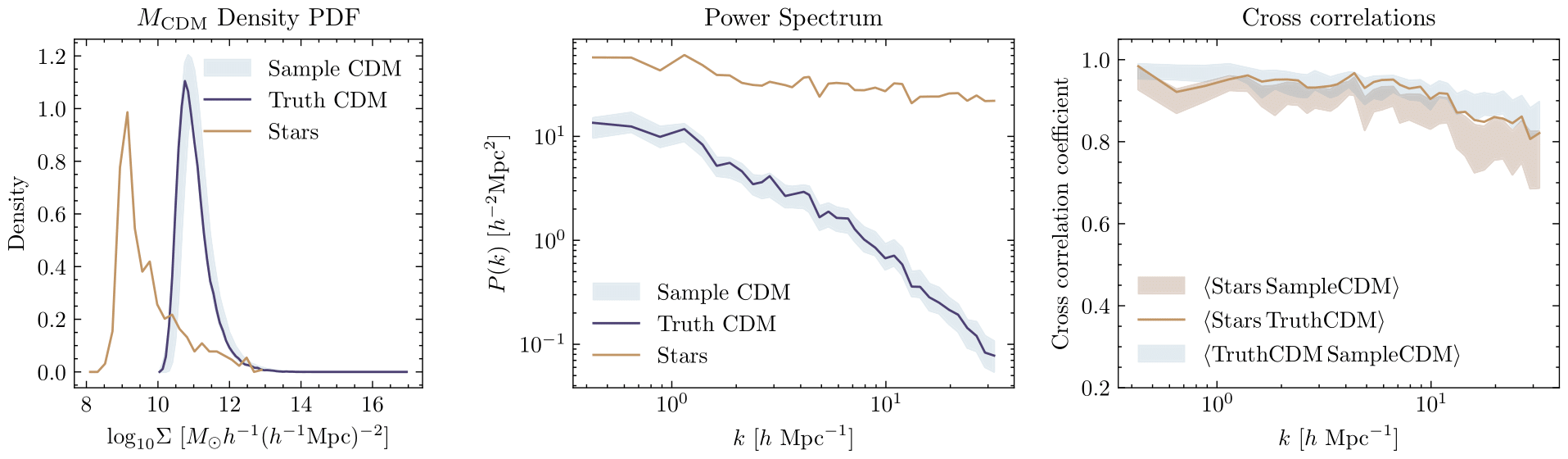
(Probabilistic) reconstruction of Dark Matter
"Probabilistic Reconstruction of Dark Matter fields from galaxies using diffusion models" Victoria Ono, Core Francisco Park, Nayantara Mudur, Yueying Ni, Carolina Cuesta-Lazaro (in prep)
pϕ(xDM∣xStars)
p_\phi(x_\mathrm{DM}|x_\mathrm{Stars})
Hybrid hydro simulators?
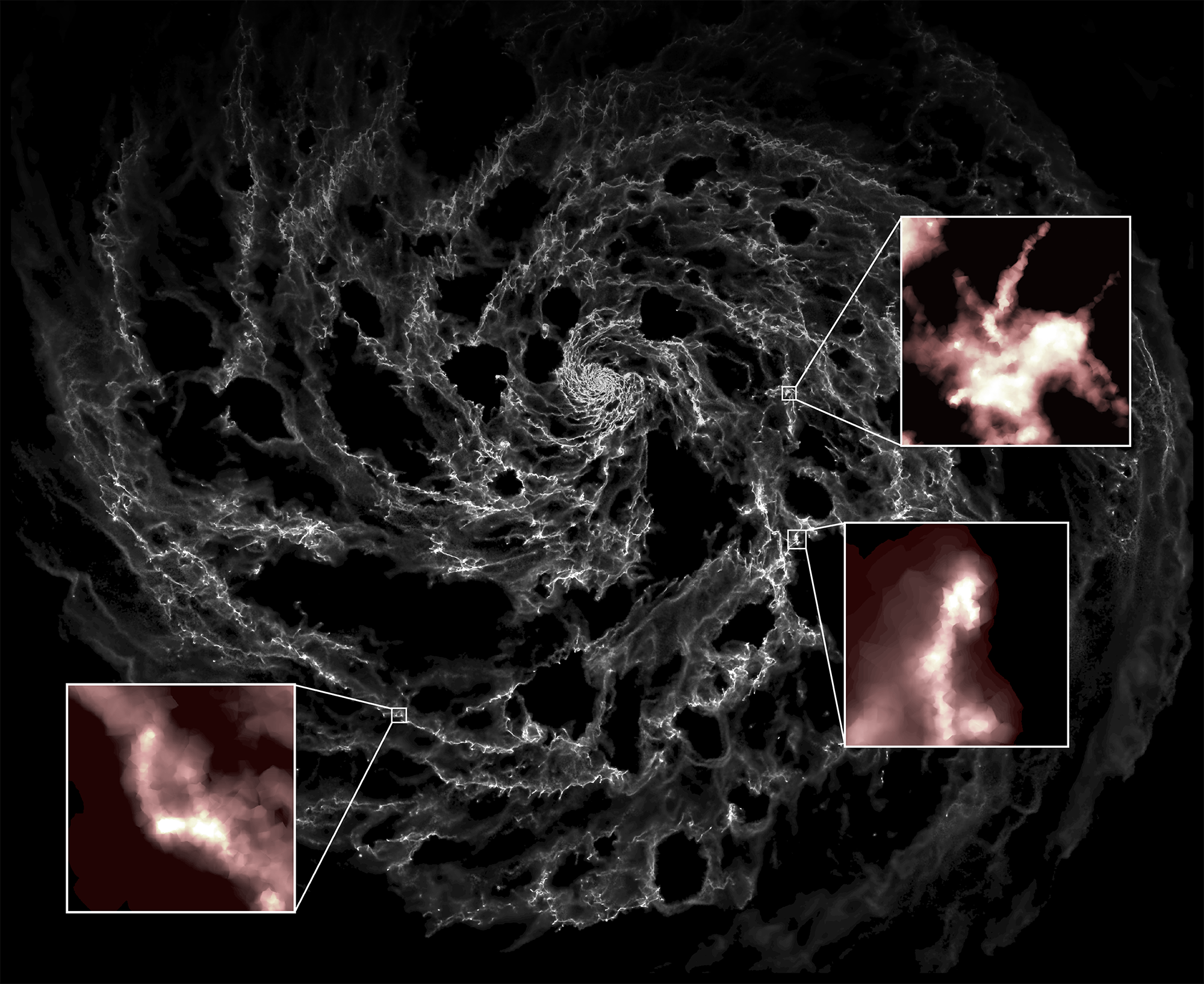
Hybrid simulators
Nbody
Slow
Non-differentiable
Particle mesh
Accurate
Fast
Differentiable
Missing small scales
Nbodyify
Fast
Differentiable
Accurate
"Nbodyify: adaptive mesh corrections for PM simulations" Carolina Cuesta-Lazaro, Chirag Modi (in prep)
dadx=a3E(a)1v
\frac{\mathrm{d} \mathbf{x}}{\mathrm{d} a } = \frac{1}{a^3 E(a)}\mathbf{v}
dadv=a2E(a)1F(x,a)
\frac{\mathrm{d} \mathbf{v}}{\mathrm{d} a } = \frac{1}{a^2 E(a)}\mathbf{F}(\mathbf{x},a)
Fθ(x,a)=23Ωm∇[ϕPM(x)+ϕθcorr(x,a,ϕPM,δPM)]
\mathbf{F}_\theta(\mathbf{x},a) = \frac{3 \Omega_m}{2} \nabla \left[\phi^\mathrm{PM}(\mathbf{x}) + \phi^\mathrm{corr}_\theta(\mathbf{x}, a, \phi^\mathrm{PM}, \delta^\mathrm{PM}) \right]
F(x,a)=23Ωm∇ϕPM(x)
\mathbf{F}(\mathbf{x},a) = \frac{3 \Omega_m}{2} \nabla \phi^\mathrm{PM}(\mathbf{x})
Gravitational evolution ODE
Particle-mesh
Hybrid Simulator
Low Resolution
CNN learned features
ϕcorr(x)=gθ({CiC−1(hθ(x)),fθ(a)})
\phi_\mathrm{corr}(x) = g_\theta \left ( \{ \mathrm{CiC}^{-1}(h_\theta(x)), f_\theta(a) \} \right)
h(16D)
h (16D)
δLR
\delta_\mathrm{LR}
ϕLR
\phi_\mathrm{LR}
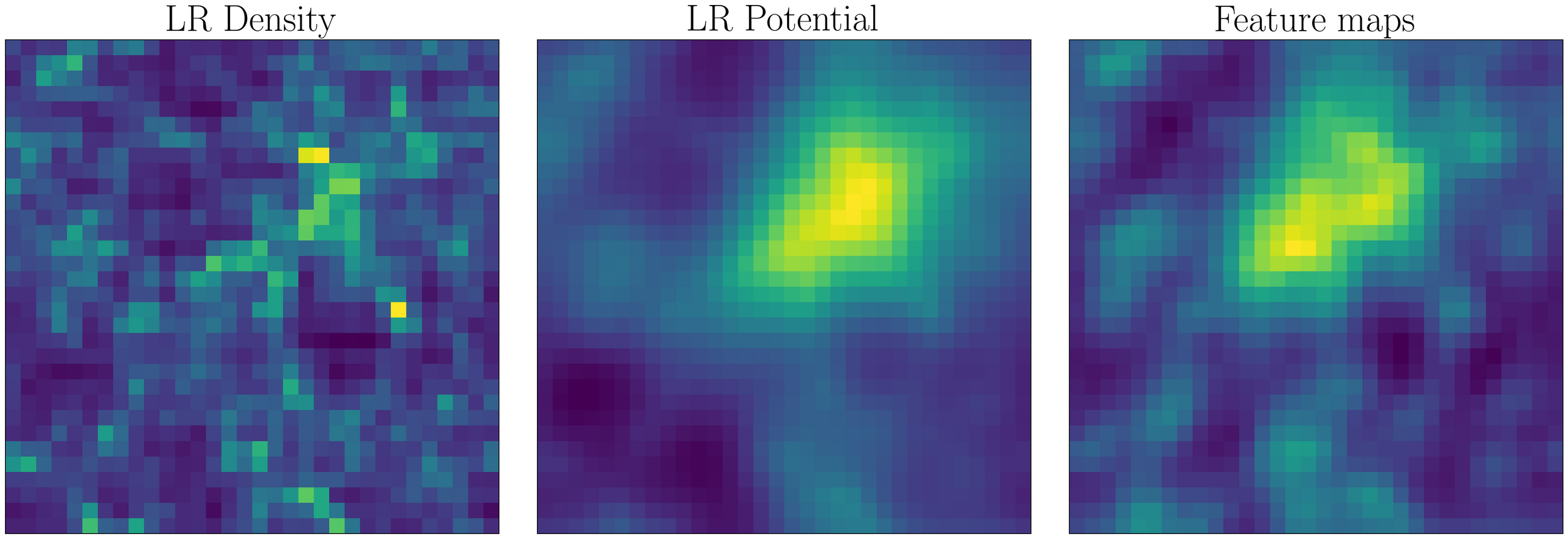
Emulation
x∼p(x∣y)
x \sim p(x|y)
Likelihood estimation
p(θ∣xobs)
p(\theta|x_\mathrm{obs})
Model uncertainties
Hybrid simulators?
logp(x)=
\log p(\boldsymbol{x}) =
≥Eqϕ(z∣x)[logqϕ(z∣x)p(x,z)]
\geq \mathbb{E}_{q_{\boldsymbol{\phi}}(\boldsymbol{z}\mid\boldsymbol{x})}\left[\log\frac{p(\boldsymbol{x}, \boldsymbol{z})}{q_{\boldsymbol{\phi}}(\boldsymbol{z}\mid\boldsymbol{x})}\right]
Eqϕ(z∣x)[logqϕ(z∣x)p(x,z)]+DKL(qϕ(z∣x)∣∣p(z∣x))
\mathbb{E}_{q_{\boldsymbol{\phi}}(\boldsymbol{z}\mid\boldsymbol{x})}\left[\log\frac{p(\boldsymbol{x}, \boldsymbol{z})}{q_{\boldsymbol{\phi}}(\boldsymbol{z}\mid\boldsymbol{x})}\right] + \mathcal{D}_{\text{KL}}(q_{\boldsymbol{\phi}}(\boldsymbol{z}\mid\boldsymbol{x}) \mid\mid p(\boldsymbol{z}\mid\boldsymbol{x}))
Evidence Lower Bound
Distance to true posterior
qθ(z∣x)≈p(z∣x)
q_\theta(z|x) \approx p(z|x)
Find
1. ELBO is a lower bound of the evidence
2. Maximising ELBO = Minimising KL
Maximise ELBO to maximise ev/likelihood
Maximise ELBO to approximate true posterior
Generative Models in Astrophysics Carol Cuesta-Lazaro IAIFI Fellow - Yale Data Science Seminar
deck
By carol cuesta
deck
- 367
