From Zero to Generative

IAIFI Fellow, MIT

Carolina Cuesta-Lazaro

Art: "The art of painting" by Johannes Vermeer

Learning Generative Modelling from scratch

Cuenca

Spain

Heidelberg

Germany

Tokyo

Japan

Durham

England

Boston

US

About Myself

Medical Imaging

Epidemiology: Agent Based simulations

OBSERVED

SIMULATED

Cosmology

Simulations

HPC

Science question

Statistics ML

Natural Language

Carolina Cuesta-Lazaro IAIFI/MIT - From Zero to Generative

BEFORE

Artificial General Intelligence?

AFTER

Carolina Cuesta-Lazaro IAIFI/MIT - From Zero to Generative

https://parti.research.google​​​​​​​

A portrait photo of  a kangaroo wearing an orange hoodie and blue sunglasses standing on the grass in front of the Sydney Opera House holding a sign on the chest that says Welcome Friends!

Carolina Cuesta-Lazaro IAIFI/MIT - From Zero to Generative

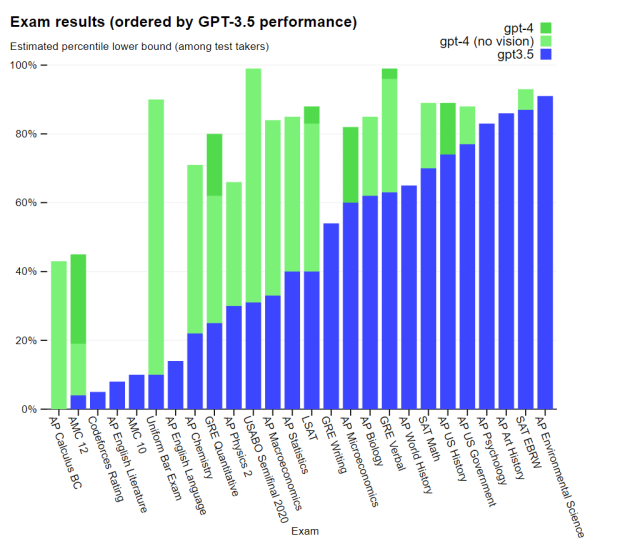
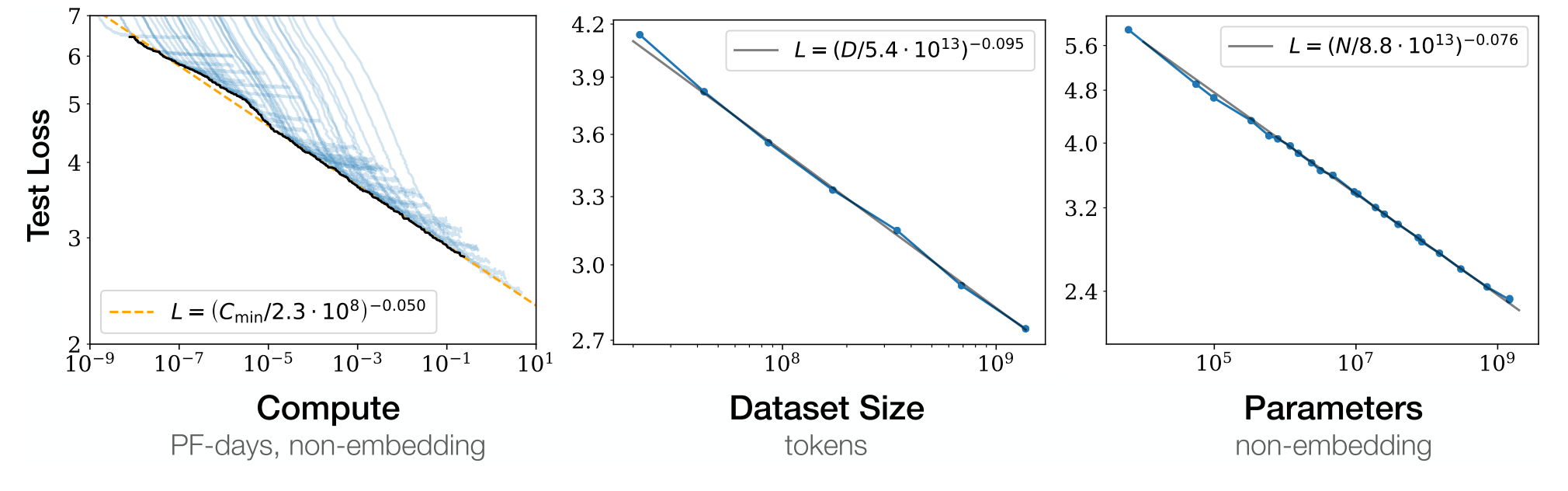
Scaling laws and emergent abilities

"Scaling Laws for Neural Language Models" Kaplan et al

Carolina Cuesta-Lazaro IAIFI/MIT - From Zero to Generative

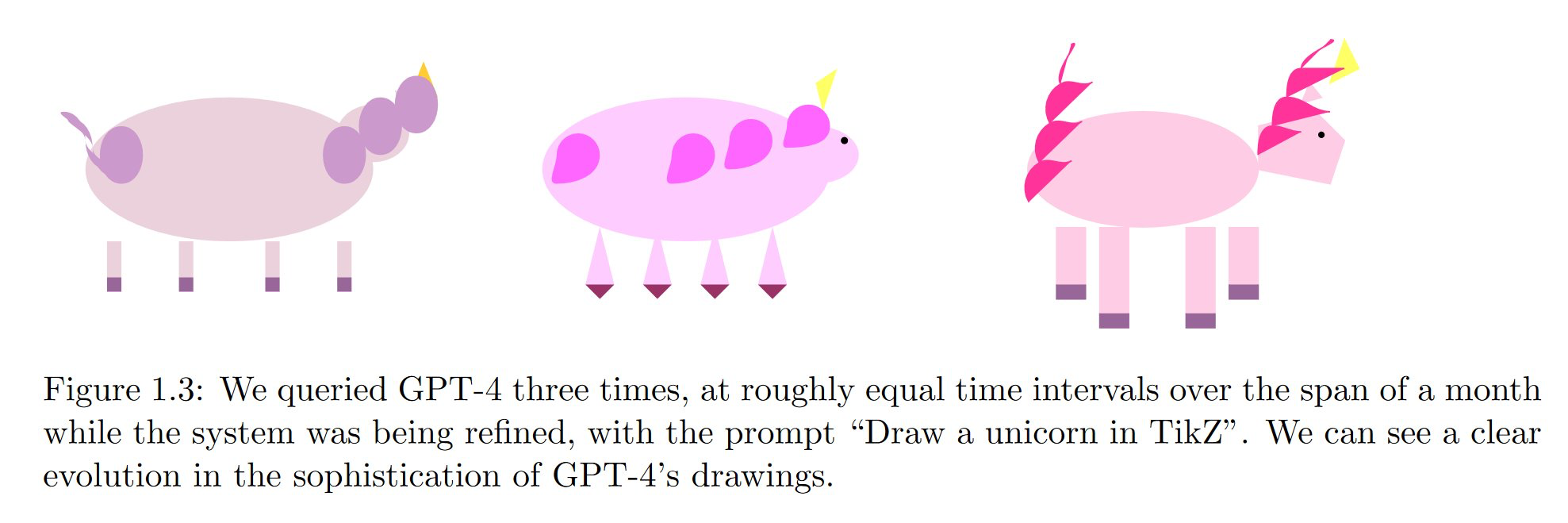
"Sparks of Artificial General Intelligence: Early experiments with GPT-4" Bubeck et al

Produce Javascript code that creates a random graphical image that looks like a painting of Kandinsky

Draw a unicorn in TikZ

Carolina Cuesta-Lazaro IAIFI/MIT - From Zero to Generative

Abstraction and Reasoning Corpus for Artificial General Intelligence (ARC-AGI)

Carolina Cuesta-Lazaro IAIFI/MIT - From Zero to Generative

Today's Plan

1. Recap of the Machine Learning building blocks

2. Learning to classify

BREAK

3. Tutorial: Build your first classifier

4. Introduction to Generative Models

5. Tutorial: Build your first generative model

(if time permits)

BREAK

Carolina Cuesta-Lazaro IAIFI/MIT - From Zero to Generative

The building blocks: 1. Data

Cosmic Cartography

(Pointclouds)

MNIST

(Images)

Wikipedia

(Text)

Carolina Cuesta-Lazaro IAIFI/MIT - From Zero to Generative

1024x1024

The curse of dimensionality

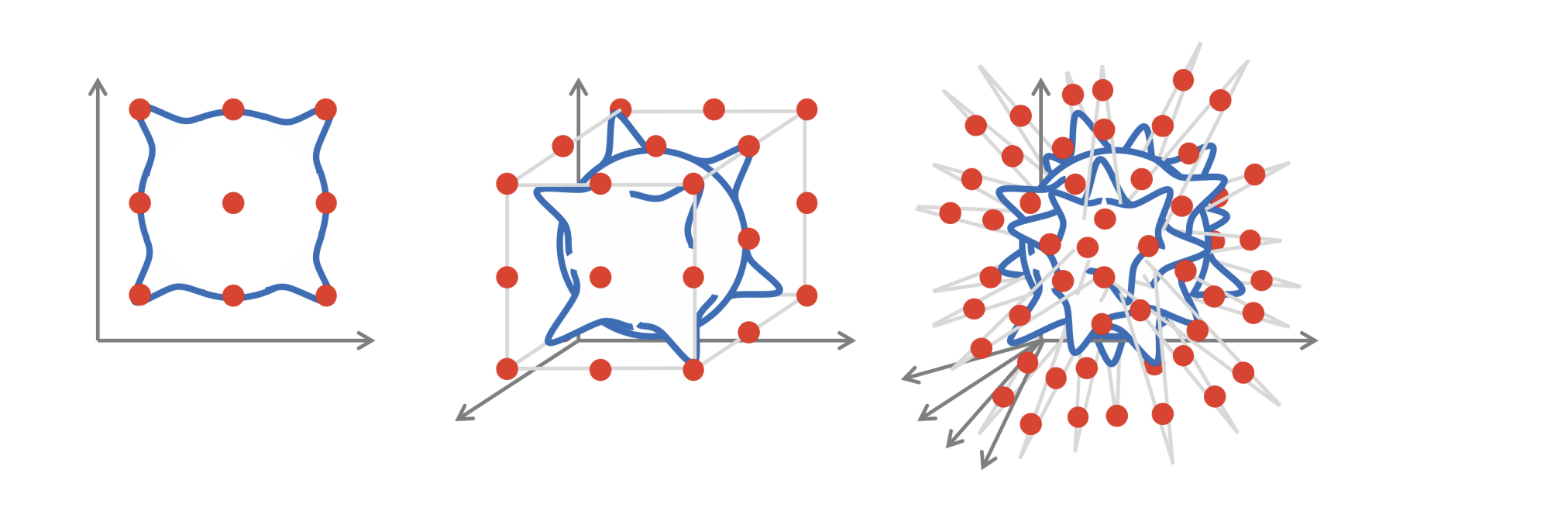
Inductive biases!

Carolina Cuesta-Lazaro IAIFI/MIT - From Zero to Generative

The building blocks: 2. Architectures

"Geometric Deep Learning Grids, Groups, Graphs, Geodesics, and Gauges" Bronstein et al

Carolina Cuesta-Lazaro IAIFI/MIT - From Zero to Generative

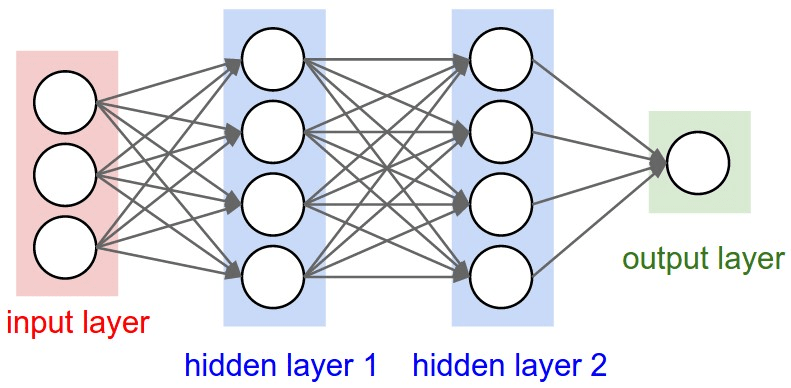
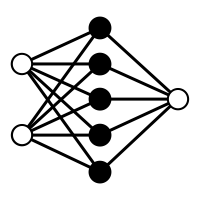
Multilayer Perceptron

Image Credit: CS231n Convolutional Neural Networks for Visual Recognition
4

Pixel 1

Pixel 2

Pixel N

Carolina Cuesta-Lazaro IAIFI/MIT - From Zero to Generative

Convolutional Neural Networks

Inductive bias: Translation Invariance

Data Representation: Images

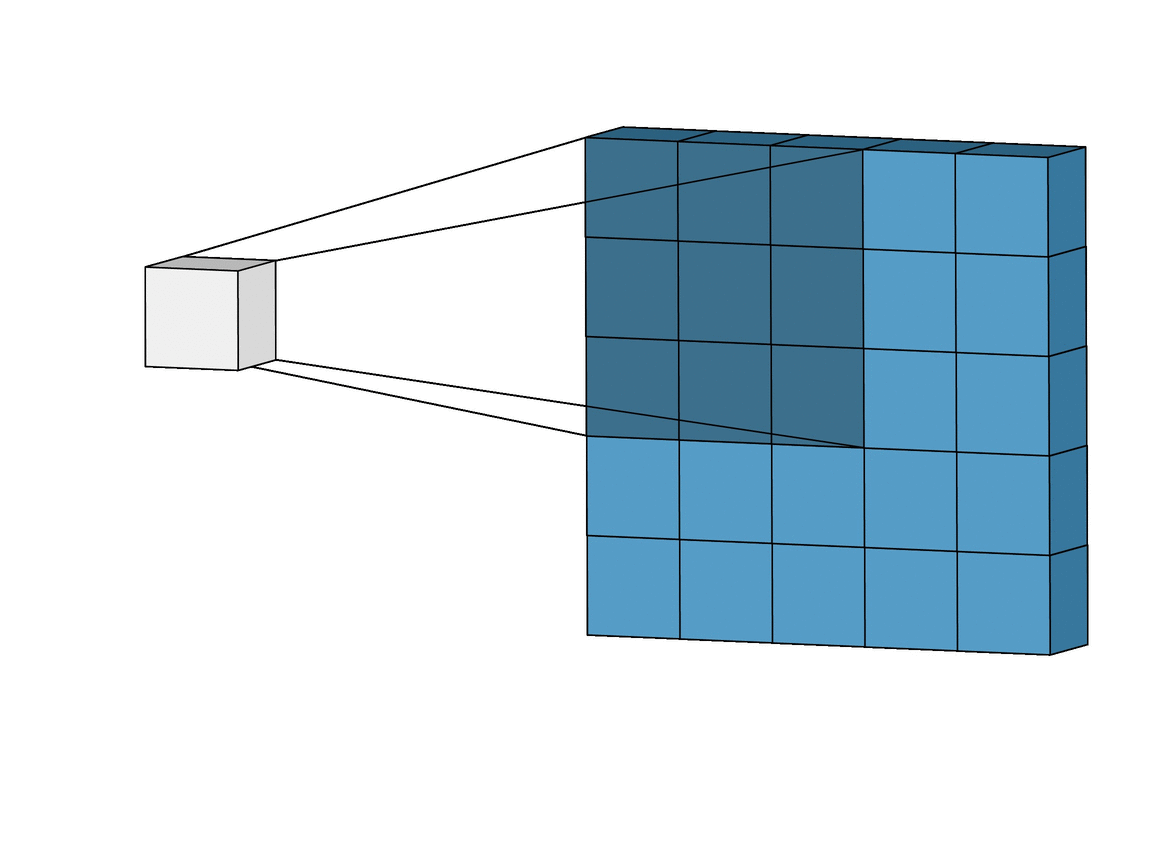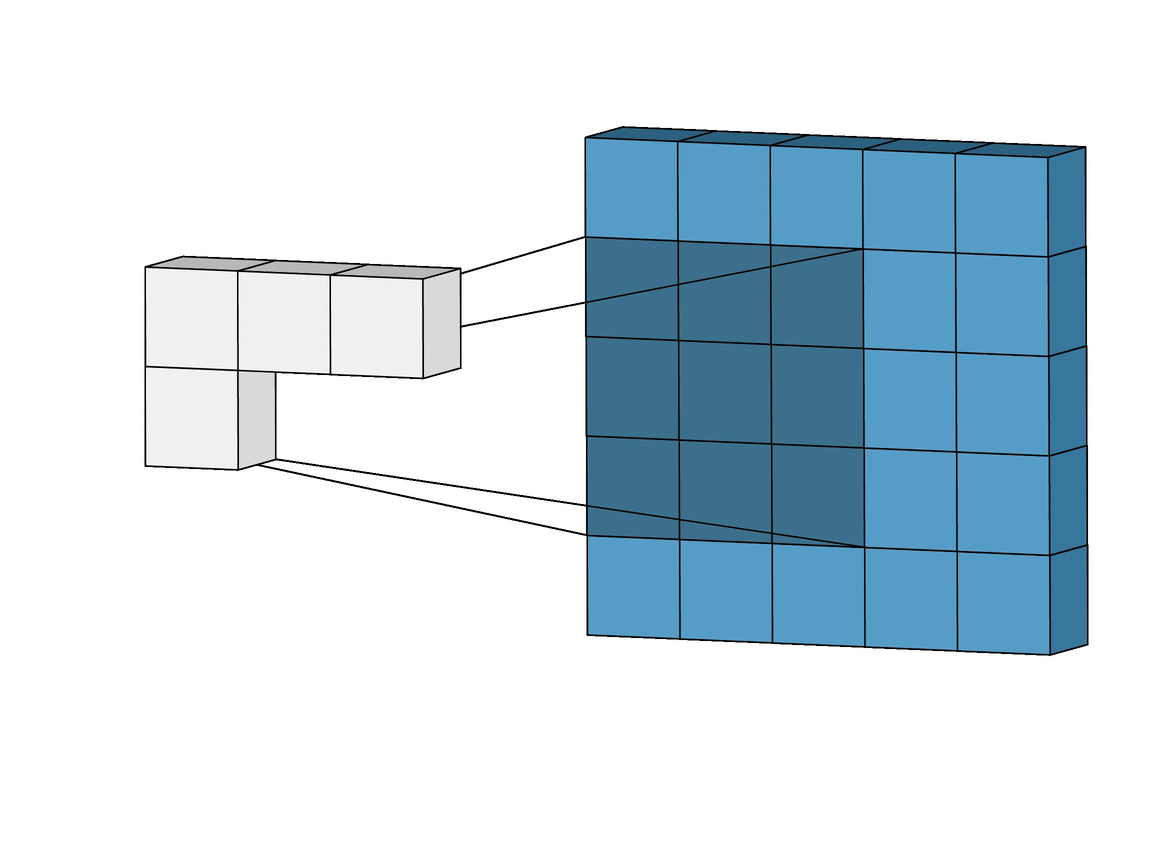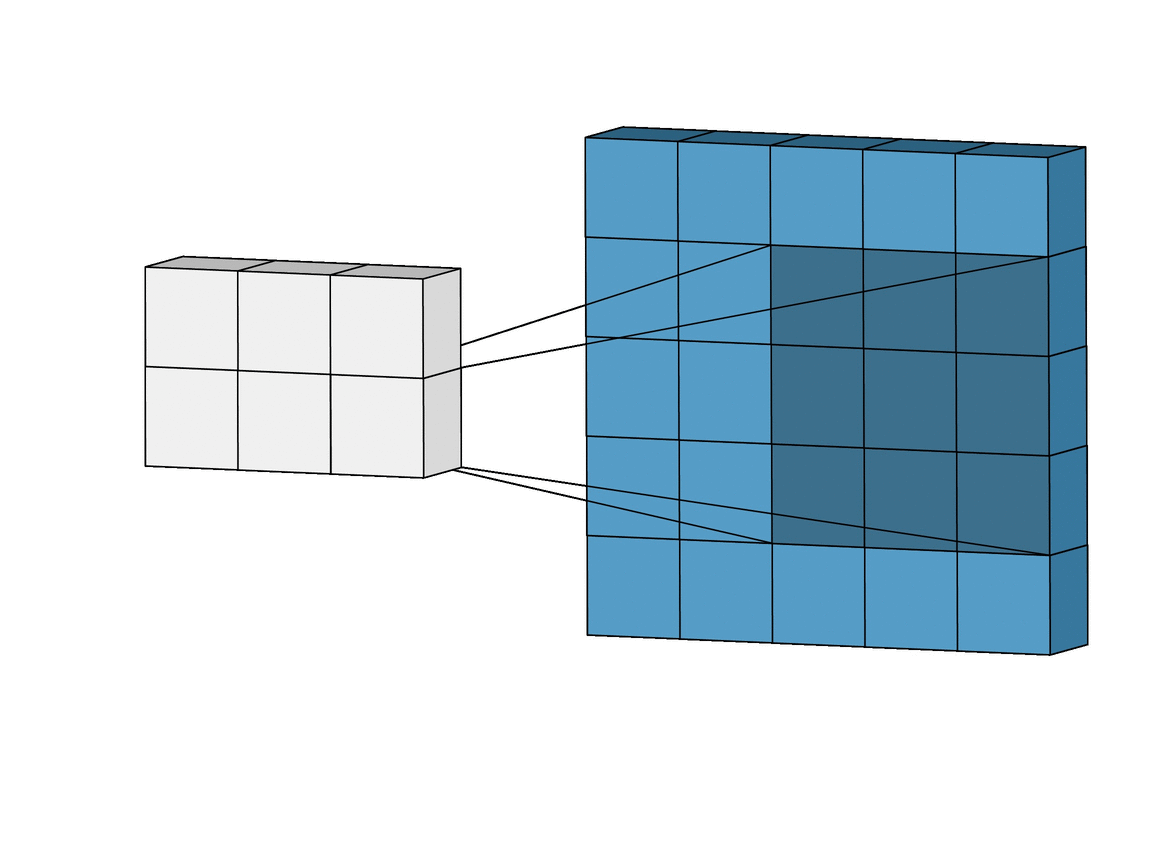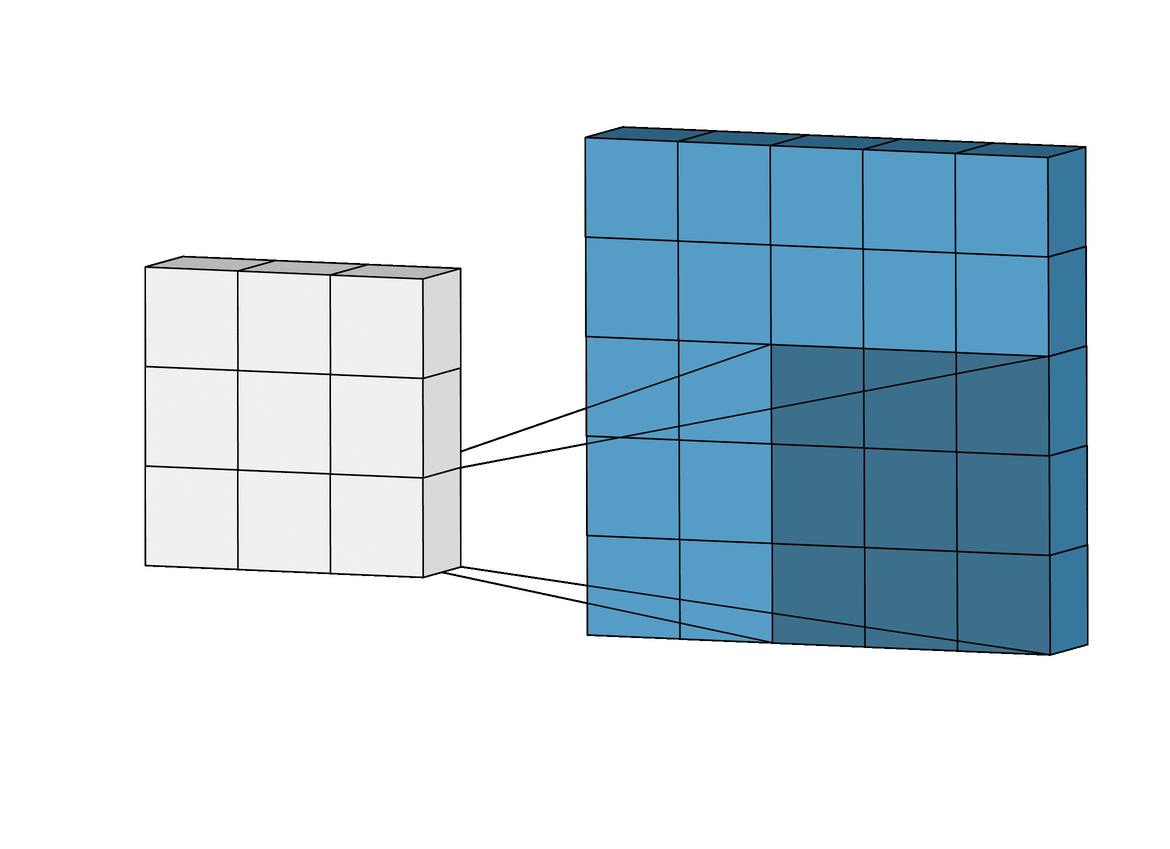
Image Credit: Irhum Shakfat "Intuitively Understanding Convolutions for Deep Learning"

Carolina Cuesta-Lazaro IAIFI/MIT - From Zero to Generative

Inductive bias: Permutation Invariance

Data Representation: Sets, Pointclouds

Deep sets

+
+
= 4
f(x) = f(P(x))
f(x) = \oplus_{i=0}^N h_\theta(x_i)

Carolina Cuesta-Lazaro IAIFI/MIT - From Zero to Generative

+
+
= 4

Transformers might be the unifying architecture!

 

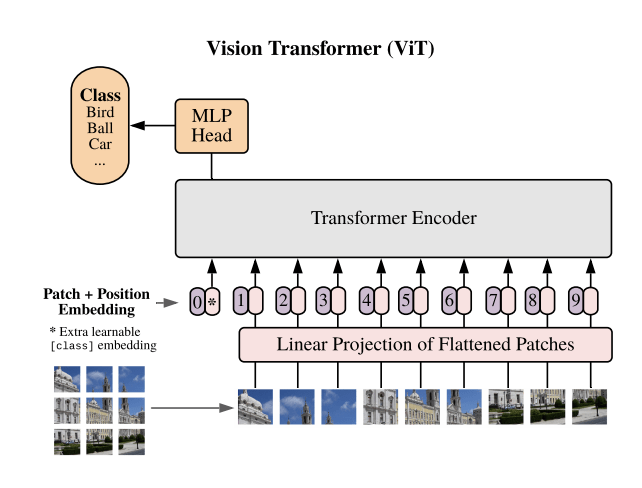
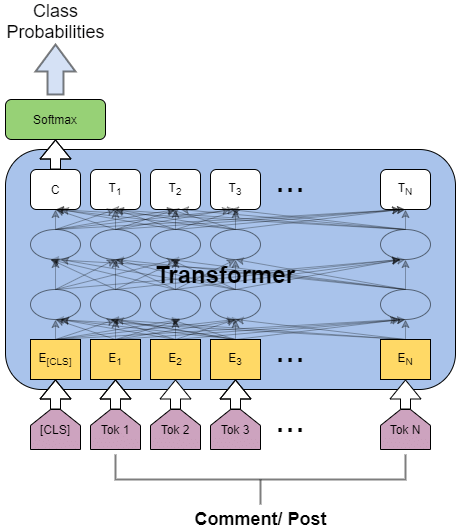
Text

Images

Carolina Cuesta-Lazaro IAIFI/MIT - From Zero to Generative

The building blocks: 3. Loss function

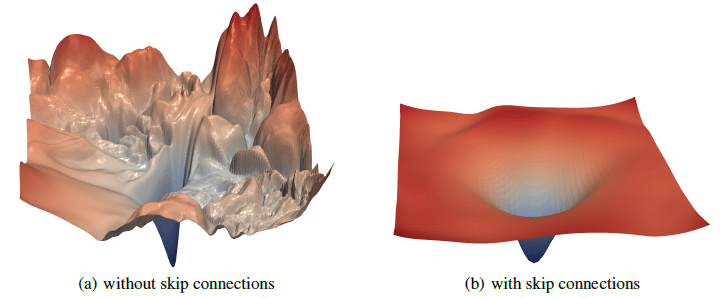
Image Credit: "Visualizing the loss landscape of neural networks" Hao Li et al

Carolina Cuesta-Lazaro IAIFI/MIT - From Zero to Generative

The building blocks: 4. The Optimizer

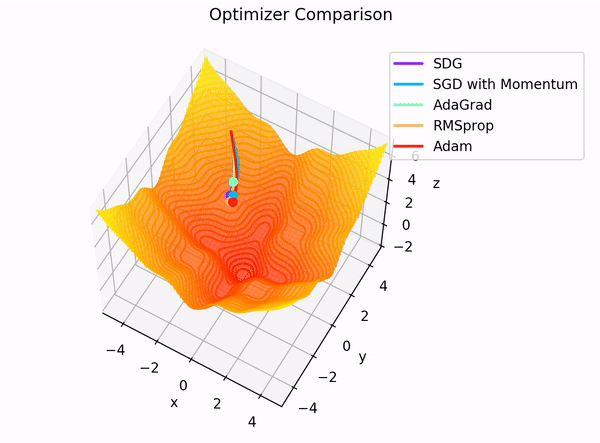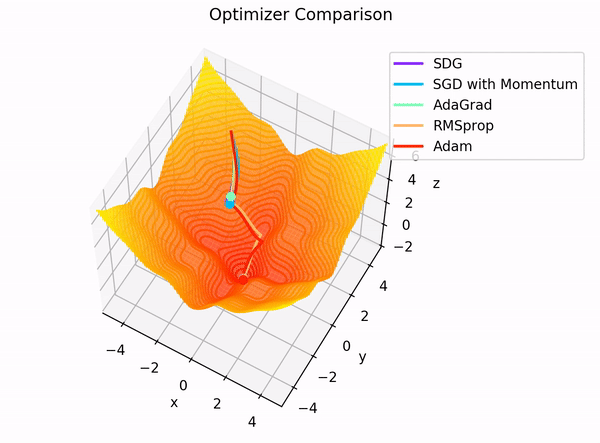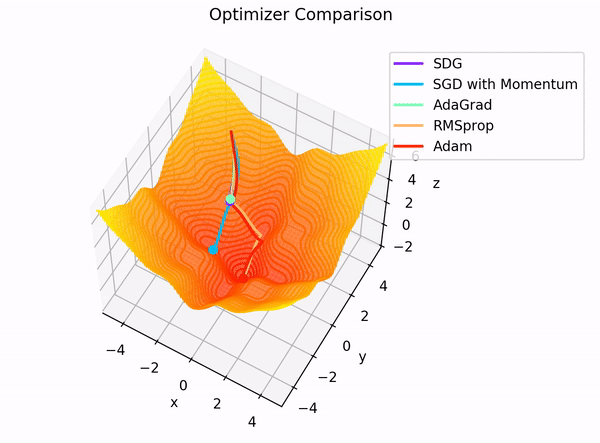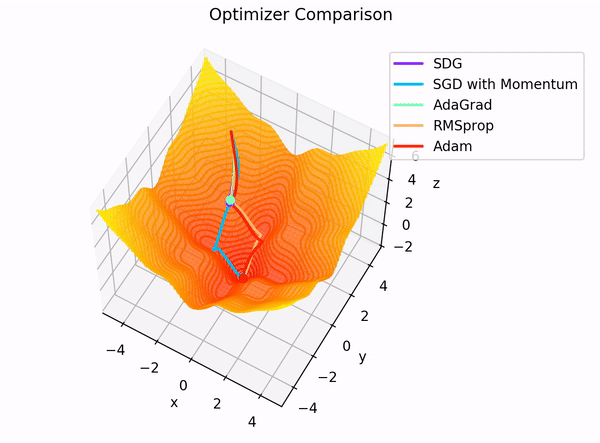
Image Credit: "Complete guide to Adam optimization" Hao Li et al

Carolina Cuesta-Lazaro IAIFI/MIT - From Zero to Generative

Tutorial 1: Learning to classify

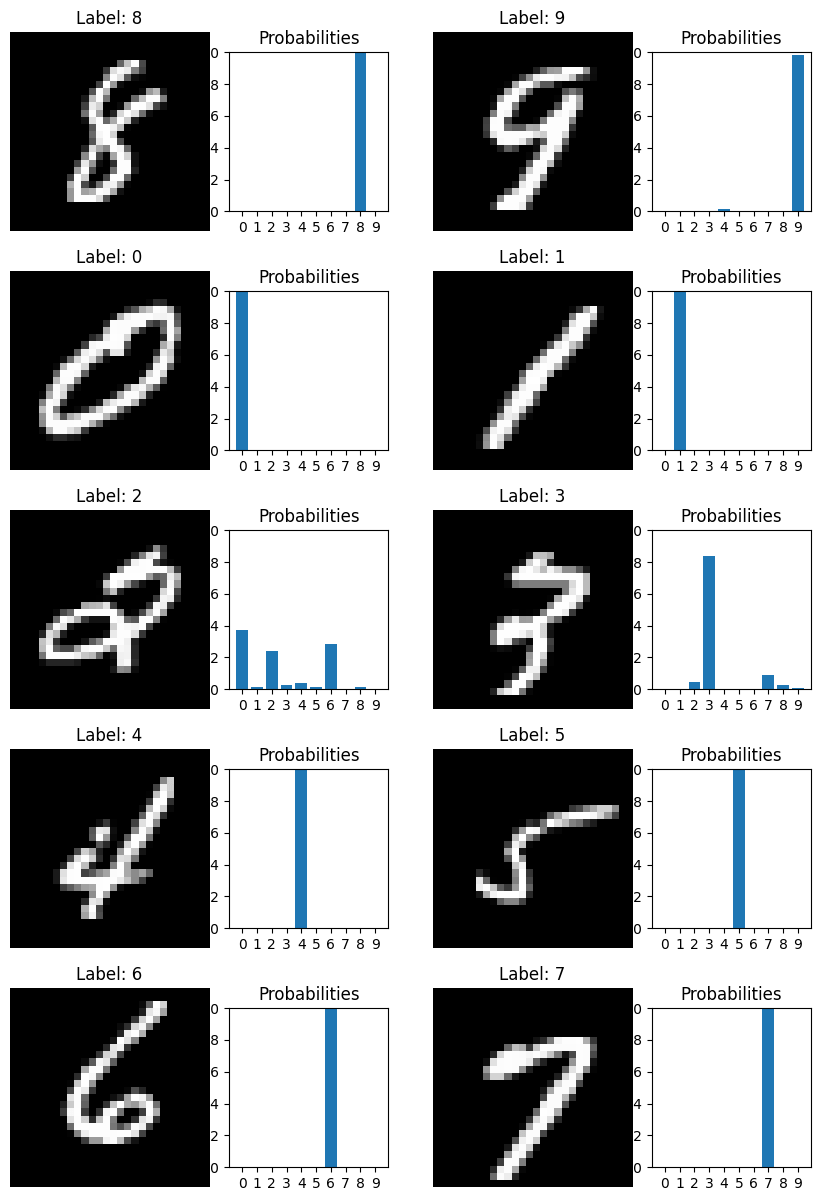
Carolina Cuesta-Lazaro IAIFI/MIT - From Zero to Generative

How do we output a probability?

0 \leq p_i(x) \leq 1
\sum_i^C p(x_i) = 1
\text{softmax}(z_i) = \frac{e^{z_i}}{\sum_{j=1}^K e^{z_j}}

Carolina Cuesta-Lazaro IAIFI/MIT - From Zero to Generative

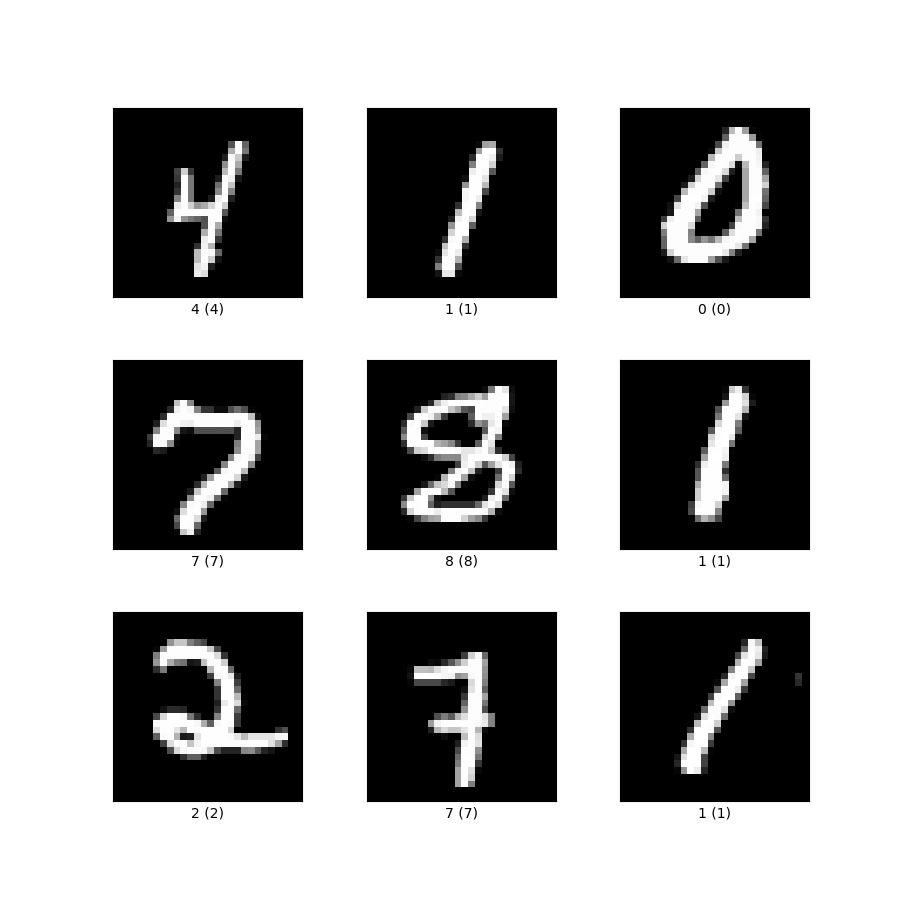
Pixel 1

Pixel 2

Pixel N

p Class 1

p Class 2

p Class 10

Loss function: Cross entropy

How different are two probability distributions?

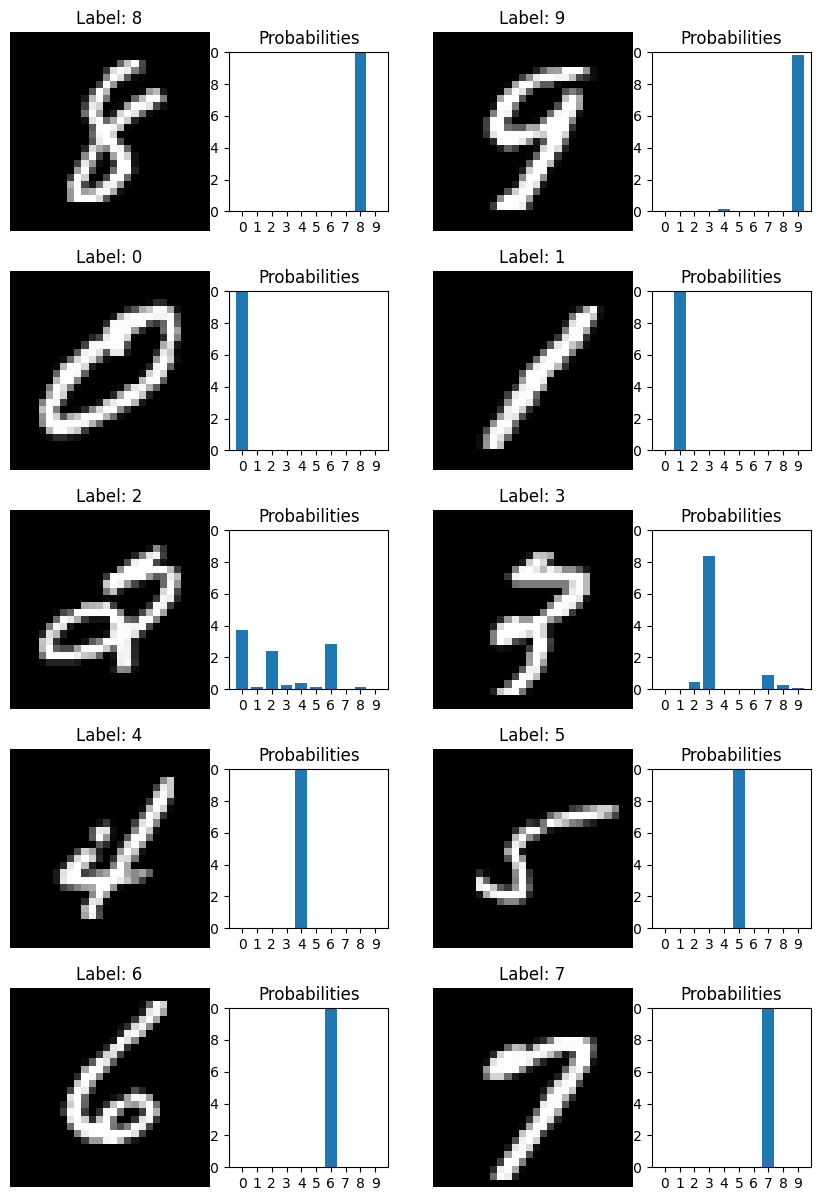
Model Prediction

if True class is for i

y_{i} = 1
y_{i} = 0

otherwise

L = - \sum_{i=1}^{C} y_{i} \log(p(\hat{y}_{i}))

Carolina Cuesta-Lazaro IAIFI/MIT - From Zero to Generative

Truth: Class = 0

True class

Predicted probability

Loss function: Cross entropy

How different are two probability distributions?

Model Prediction

Truth: Class = 0

L = - \sum_{i=1}^{C} y_{i} \log(p(\hat{y}_{i}))

Carolina Cuesta-Lazaro IAIFI/MIT - From Zero to Generative

Predicted probability

True class

p = \left[0.4, 0.01, 0.25, 0.02,0.01,0.02, 0.25, 0., 0.04, 0. \right]

Loss function: Cross entropy

How different are two probability distributions?

Model Prediction

Truth: Class = 0

L = - \sum_{i=1}^{C} y_{i} \log(p(\hat{y}_{i}))

Carolina Cuesta-Lazaro IAIFI/MIT - From Zero to Generative

0.4 \times 1
0.4 \times 1 + 0.01 \times 0
0.4 \times 1 + 0.01 \times 0 + 0.25 \times 0
i = 0
i = 1
i = 2
+ ... = 0.4
import flax.linen as nn

class MLP(nn.Module):
    @nn.compact
    def __call__(self, x):
      	# Linear
        x = nn.Dense(features=64)(x)
        # Non-linearity
        x = nn.silu(x)
        # Linear
        x = nn.Dense(features=64)(x)
        # Non-linearity
        x = nn.silu(x)
        # Linear
        x = nn.Dense(features=2)(x)
        return x

model = MLP()

Jax Models

import jax.numpy as jnp

example_input = jnp.ones((1,4))
params = model.init(jax.random.PRNGKey(0), example_input) 
y = model.apply(params, example_input)

Architecture

Parameters

Call

A 2D animation of a folk music band composed of anthropomorphic autumn leaves, each playing traditional bluegrass instruments, amidst a rustic forest setting dappled with the soft light of a harvest moon

Image credit: DALL·E 3

 

1024x1024

Carolina Cuesta-Lazaro IAIFI/MIT - From Zero to Generative

p(x)
p(y|x)
p(x|y) = \frac{p(y|x)p(x)}{p(y)}
p(x|y)

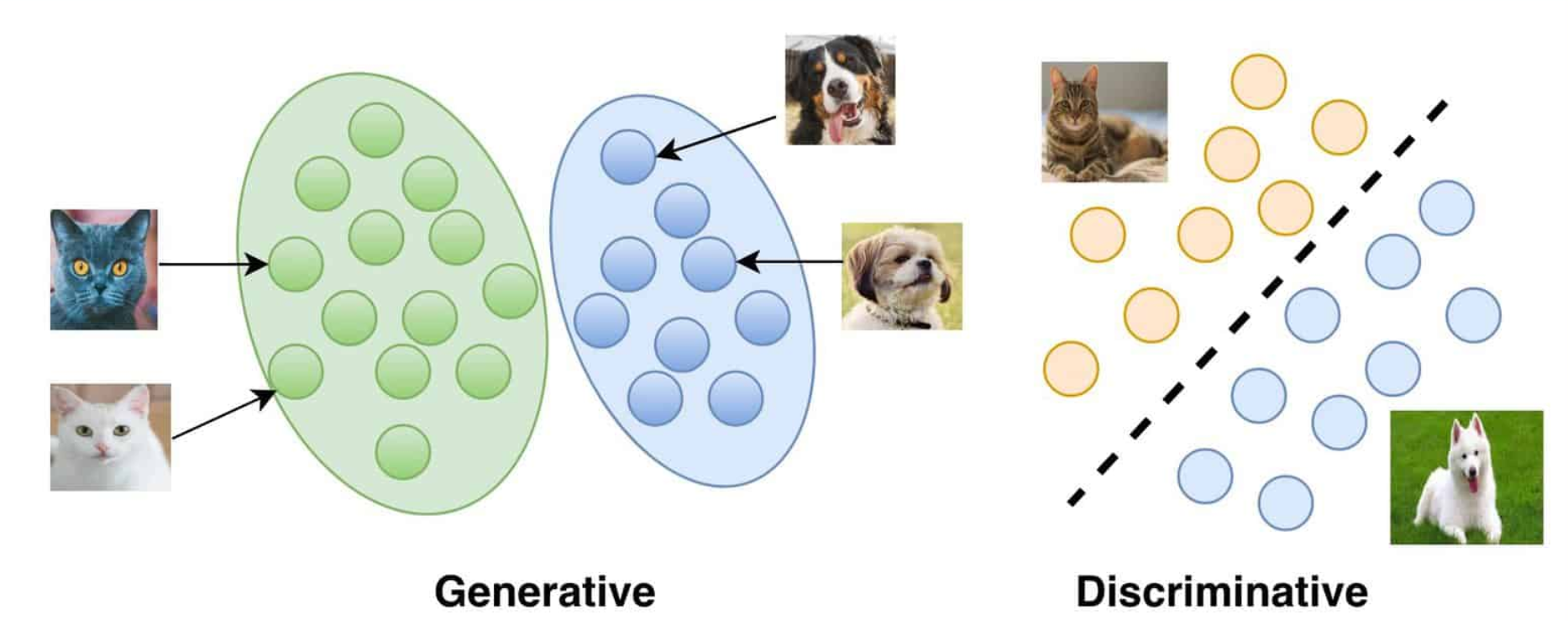
Generation vs Discrimination

Carolina Cuesta-Lazaro IAIFI/MIT - From Zero to Generative

p_\phi(x)

Data

A PDF that we can optimize

Maximize the likelihood of the data

Generative Models

Carolina Cuesta-Lazaro IAIFI/MIT - From Zero to Generative

Maximize the likelihood of the training samples

\hat \theta = \argmax \left[ \log p_\theta (x_\mathrm{train}) \right]
x_1
x_2

Model

p_\theta(x)

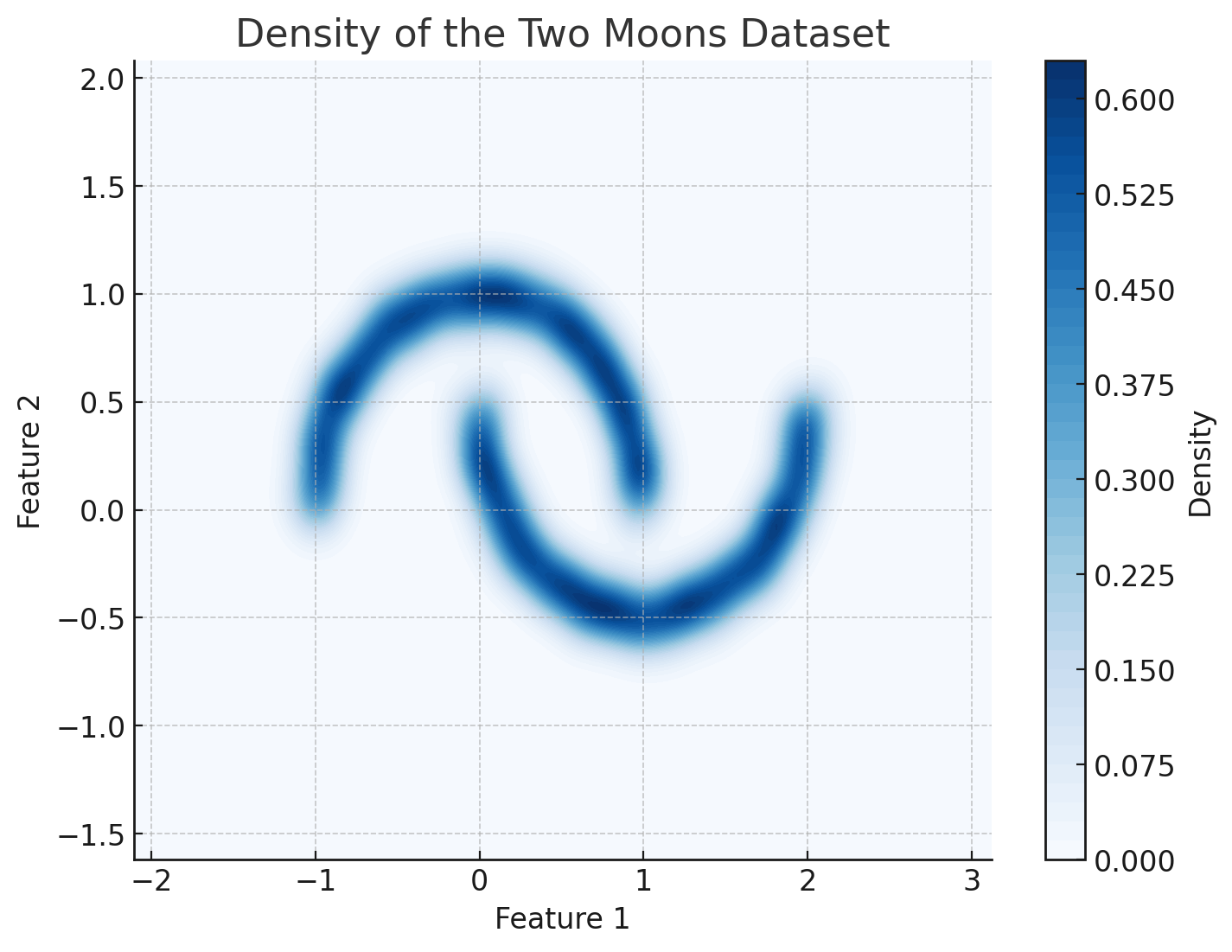
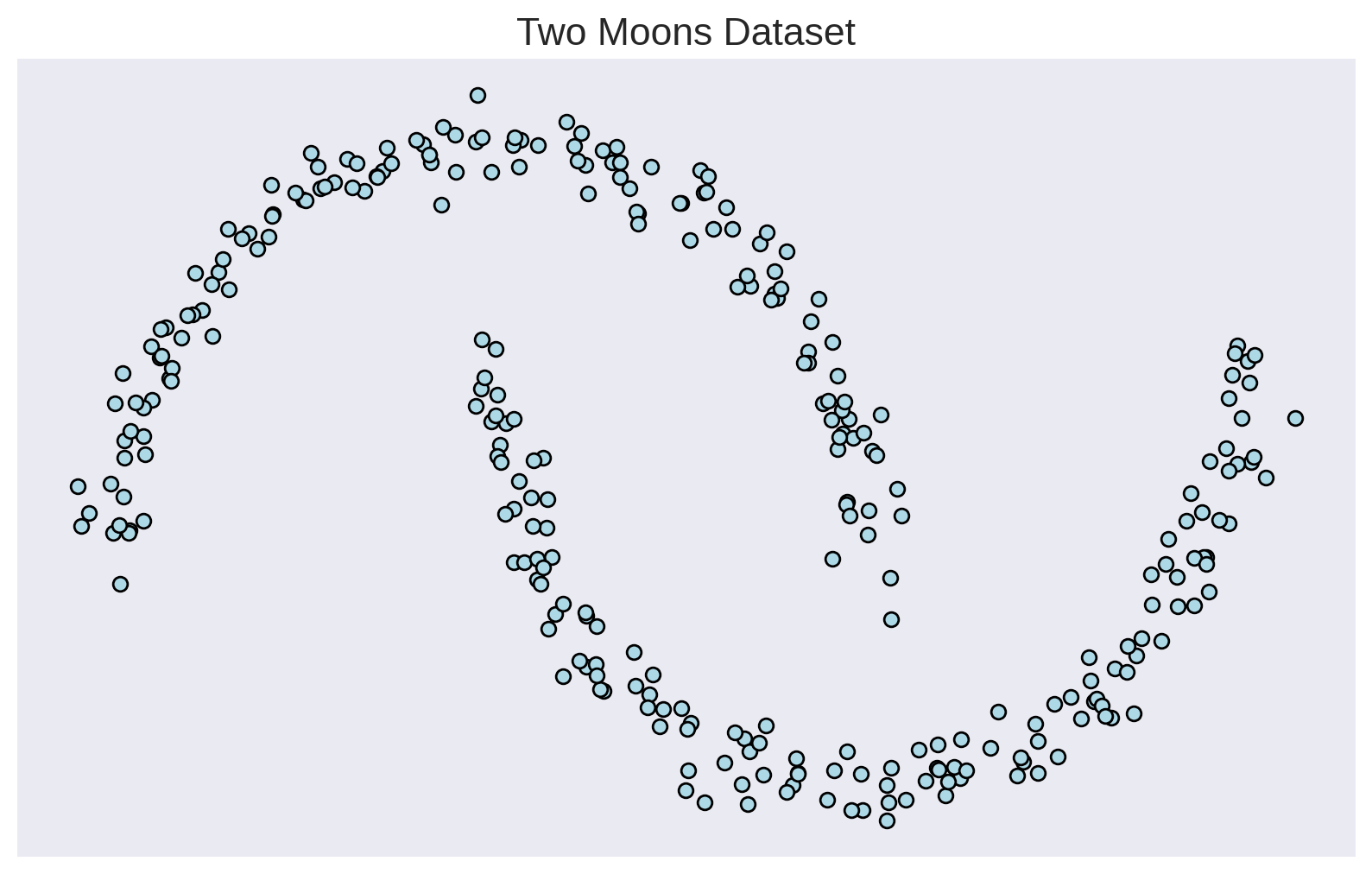
Training Samples

x_\mathrm{train}

Generative Models 101

Carolina Cuesta-Lazaro IAIFI/MIT - From Zero to Generative

x_1
x_2

Trained Model

p_\theta(x)

Evaluate probabilities

Low Probability

High Probability

Generate Novel Samples

Carolina Cuesta-Lazaro IAIFI/MIT - From Zero to Generative

Change of variables

X \sim \mathcal{N}(0,1)

sampled from a Gaussian distribution with mean 0 and variance 1

Y = g(X) = a X + b

How is 

Y

distributed?

p_Y(y) = p_X(g^{-1}(y)) \left| \frac{dg^{-1}(y)}{dy}\right|
P(Y\le y) = P(g(X)\le y) = P(X\le g^{-1}(y))
\mathrm{CDF}_Y = \mathrm{CDF}_{X}(g^{-1}(y))

Base distribution

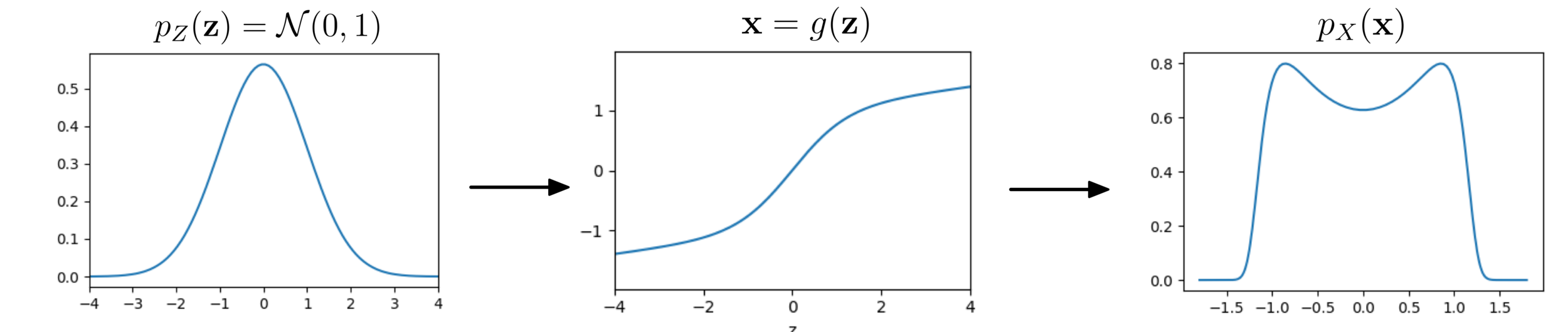
Target distribution

p_X(x) = p_Z(z) \left| \frac{dz}{dx}\right|
Z \sim \mathcal{N} (0,1) \rightarrow g(z) \rightarrow X

Invertible transformation

z \sim p_Z(z)
p_Z(z)

Normalizing flows

Carolina Cuesta-Lazaro IAIFI/MIT - From Zero to Generative

\mathrm{Uniform(0,1)} \rightarrow U_1, U_2
Z_0 = \sqrt{-2 \ln U_1} \cos(2 \pi U_2)
Z_1 = \sqrt{-2 \ln U_1} \sin(2 \pi U_2)
Z_0, Z_2 \leftarrow N(0,1)

Box-Muller transform

Normalizing flows in 1934

Carolina Cuesta-Lazaro IAIFI/MIT - From Zero to Generative

x = f(z), \, z = f^{-1}(x)
p(\mathbf{x}) = p_z(f^{-1}(\mathbf{x})) \left\vert \det J(f^{-1}) \right\vert

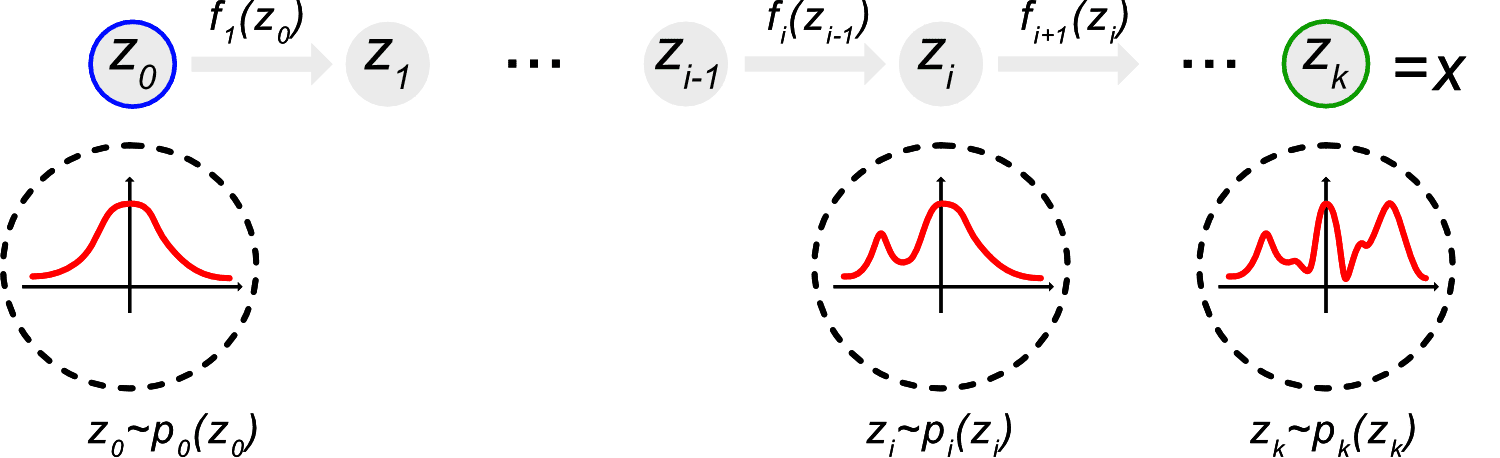
(Image Credit: Phillip Lippe)

p(x) = \int dz \, p(x|z)

z: Latent variables

Carolina Cuesta-Lazaro IAIFI/MIT - From Zero to Generative

Invertible functions aren't that common!

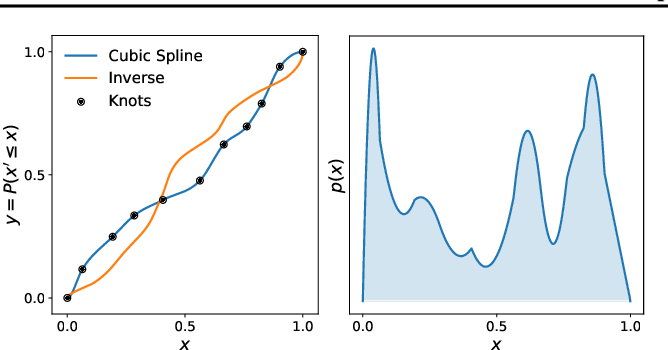
Splines

Carolina Cuesta-Lazaro IAIFI/MIT - From Zero to Generative

But ODE solutions are always invertible!

Continuous time

x_1 = x_0 + \int_0^1 v_\theta (x(t)) dt
x_0 = x_1 + \int_1^0 v_\theta (x(t)) dt

Issues NFs: Lack of flexibility

  • Invertible functions
  • Tractable Jacobians

 

\frac{dx}{dt} = v_\theta(t, x_t)

Carolina Cuesta-Lazaro IAIFI/MIT - From Zero to Generative

\frac{d x_t}{dt} = u_t(x_t)

Flow ODE

x_0
p(x_0)
p(x_1)
x_1
u_t

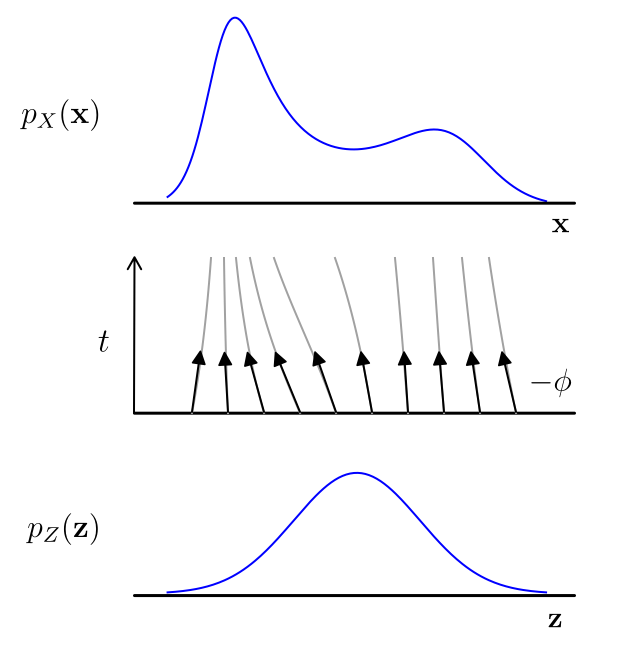
Carolina Cuesta-Lazaro IAIFI/MIT - From Zero to Generative

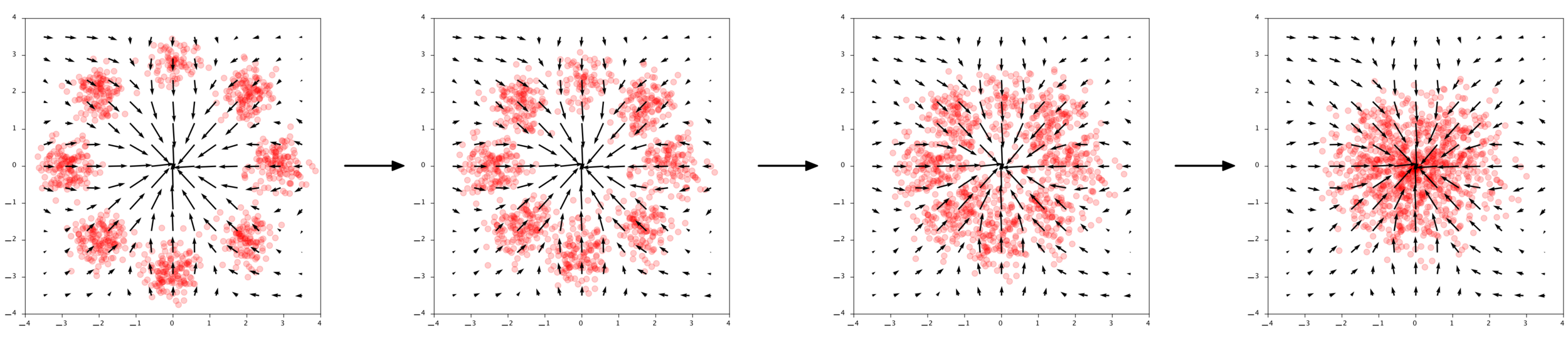
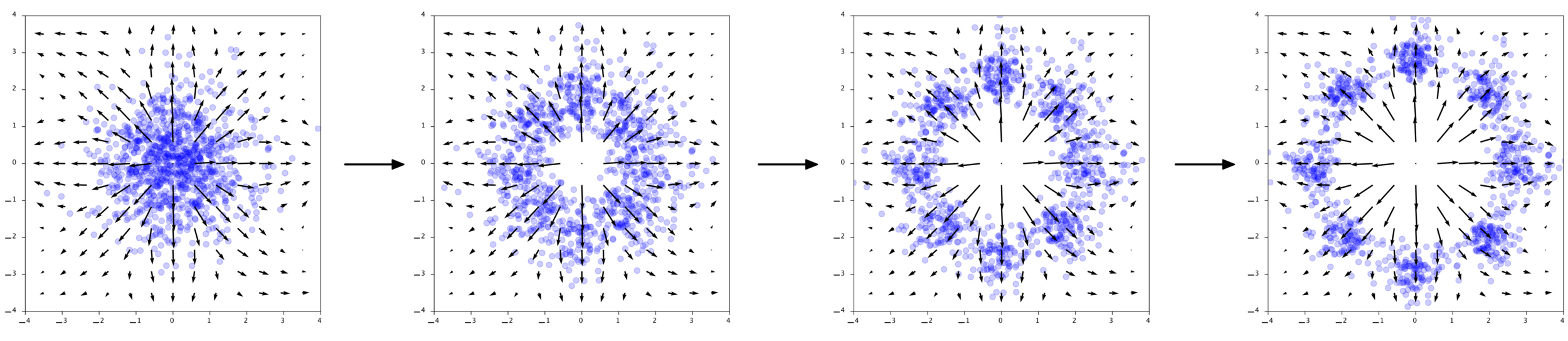
Chen et al. (2018), Grathwohl et al. (2018)
x_1 = x_0 + \int_0^1 v_\theta (x(t),t) dt

Generate

x_0
x_1

Carolina Cuesta-Lazaro IAIFI/MIT - From Zero to Generative

t

Evaluate Probability

\log p_X(x) = \log p_Z(z) + \int_0^1 \mathrm{Tr} J_v (x(t)) dt

Need to solve this expensive integral at each step during training! 

Very slow

Can we avoid it?

Carolina Cuesta-Lazaro IAIFI/MIT - From Zero to Generative

Flow matching

\mathcal{L} = \mathbb{E}_{t \sim \mathcal{U}[0, 1]} \mathbb{E}_{x \sim p_t}\left[\| u_\theta(t, x) - u(t, x) \|^2 \right]

Regress the velocity field directly!

But we need to know u. If we know u, then why learn another one?

Image Credit: "An Introduction to flow matchig" Tor Fjelde et al

Carolina Cuesta-Lazaro IAIFI/MIT - From Zero to Generative

Conditional Flow matching

x_t = (1-t) x_0 + t x_1
\mathcal{L}_\mathrm{conditional} = \mathbb{E}_{t,x_0,x_1}\left[\| u_\theta(t, x) - u(t, x_0,x_1) \|^2 \right]

Learn a conditional vector field (known at training time)

Approximate it with an unconditional one

The gradients of the losses are the same!

\nabla_\theta \mathcal{L}_\mathrm{conditional} = \nabla_\theta \mathcal{L}

Carolina Cuesta-Lazaro IAIFI/MIT - From Zero to Generative

x_0
x_1

Tutorial 2

x_0

Gaussian

MNIST 

x_1

Carolina Cuesta-Lazaro IAIFI/MIT - From Zero to Generative

Students at MIT are

Pre-trained on next word prediction

...

OVER-CAFFEINATED

NERDS

SMART

ATHLETIC

Large Language Models

Carolina Cuesta-Lazaro IAIFI/MIT - From Zero to Generative

https://www.astralcodexten.com/p/janus-simulators

How do we encode "helpful" in the loss function?

Carolina Cuesta-Lazaro IAIFI/MIT - From Zero to Generative

Step 1

Human teaches desired output

Explain RLHF

After training the model...

Step 2

Human scores outputs

+ teaches Reward model to score

it is the method by which ...

Explain means to tell someone...

Explain RLHF

Step 3

Tune the Language Model to produce high rewards!

RLHF: Reinforcement Learning from Human Feedback

Carolina Cuesta-Lazaro IAIFI/MIT - From Zero to Generative

BEFORE RLHF

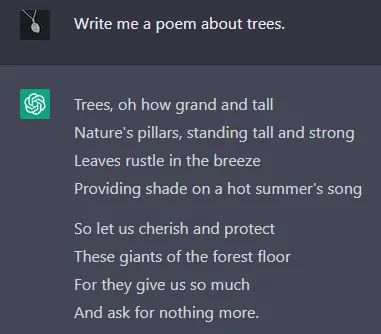
AFTER RLHF

Carolina Cuesta-Lazaro IAIFI/MIT - From Zero to Generative

Carolina Cuesta-Lazaro IAIFI/MIT - From Zero to Generative

References

cuestalz@mit.edu

Carolina Cuesta-Lazaro IAIFI/MIT - From Zero to Generative

From zero to generative - SummerSchool

By carol cuesta

From zero to generative - SummerSchool

  • 208

More from carol cuesta