Generative Solutions for Cosmic Problems
florpi
https://florpi.github.io/
IAIFI Fellow
Carol(ina) Cuesta-Lazaro
1. Observations x Simulations
2. Learning a general parametrisation for feedback
Outline
Constrained Simulations
(IC reconstruction)
3. Compressing simulation snapshots in continuous time
Inverse modelling
Data driven subgrid models
pϕ(ρDM∣ρGalaxies)
p_\phi(\rho_\mathrm{DM}|\rho_\mathrm{Galaxies})
1 to Many:
Distribution of Galaxies
Underlying Dark Matter
["Debiasing with Diffusion: Probabilistic reconstruction of Dark Matter fields from galaxies"
Ono et al (including Cuesta-Lazaro) arXiv:2403.10648]
Victoria Ono
Core Park
1. Reconstructing DM
TNG-300
True DM
Inferred DM
Size of training simulation
Galaxy Cluster
Void
[arXiv:2403.10648]
Model trained on Astrid subgrid model
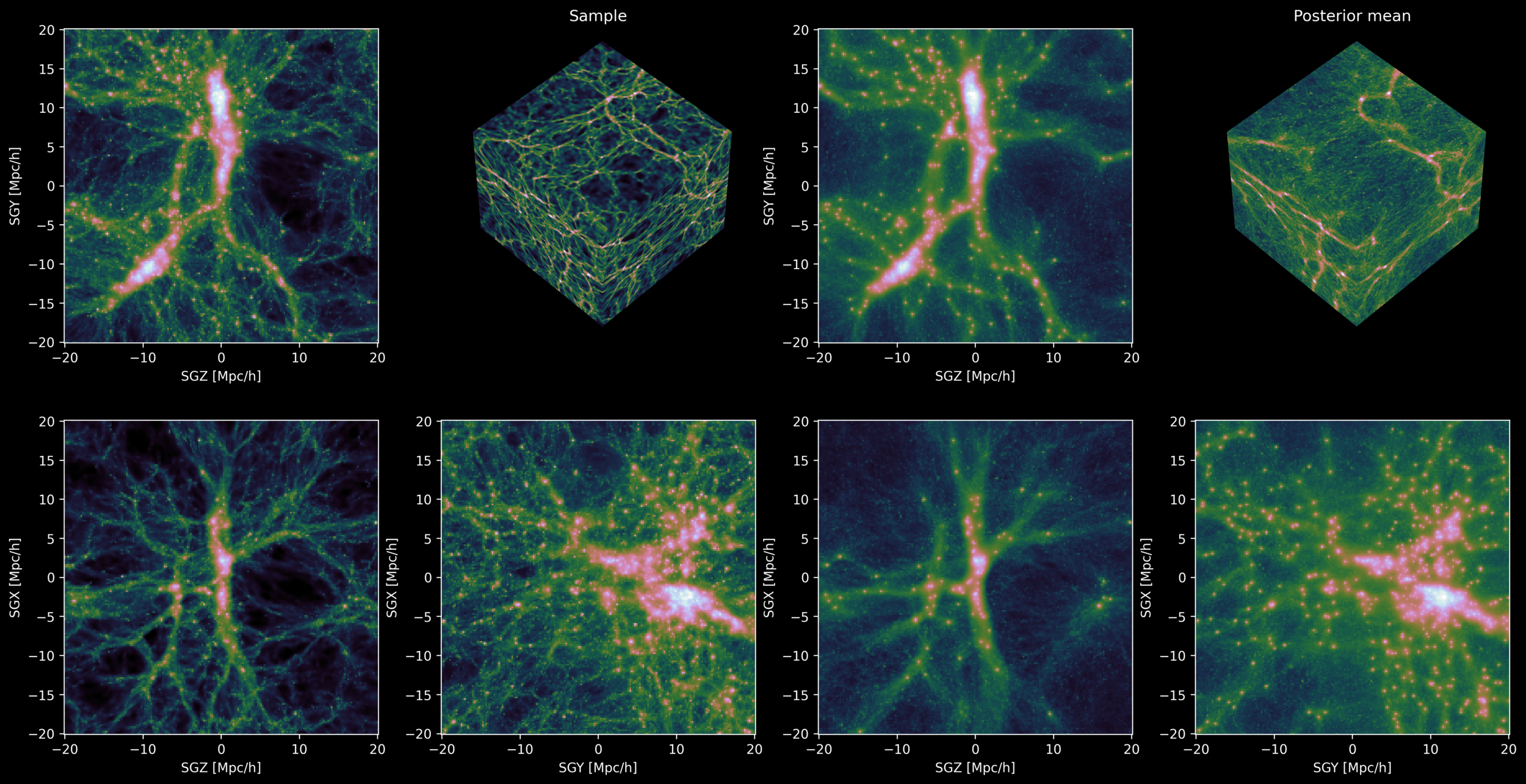
["3D Reconstruction of Dark Matter Fields with Diffusion Models: Towards Application to Galaxy Surveys" Park, Mudur, Cuesta-Lazaro et al (in-prep)]
Posterior Sample
Posterior Mean
Debiasing Cosmic Flows
p(δICs,θ∣δObs)=
p(\delta_\mathrm{ICs}, \theta|\delta_\mathrm{Obs}) =
p(δICs∣δObs)
p(\delta_\mathrm{ICs}|\delta_\mathrm{Obs})
p(θ∣δICs,δObs)
p(\theta|\delta_\mathrm{ICs},\delta_\mathrm{Obs})
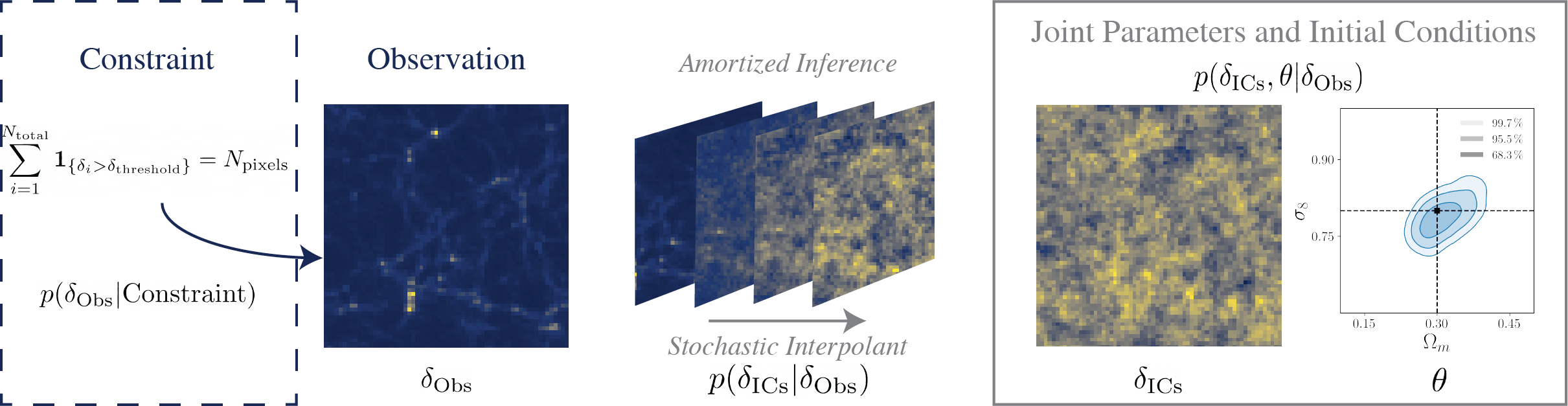
2. Reconstructing DM back in time
3. Simulating what you need (and sometimes what you want)
Guided simulations with fuzzy constraints
4. Machine learned subgrid models
1. Predictive Simulators learned subgrid models from high resolution simulations
∂t∂u=H[x,Rθ(x)]
\frac{\partial \mathbf{u}}{\partial t} = \mathcal{H}[\mathbf{x},\mathbf{R}_{\theta}(\mathbf{x})]
Hydro simulator
Subgrid model
HR:SFRθ(ρgasLR,ρstarsLR,wrotLR)
\mathrm{HR} : \mathrm{SFR}_{\theta}(\rho^\mathrm{LR}_\mathrm{gas},\rho^\mathrm{LR}_\mathrm{stars}, w^\mathrm{LR}_\mathrm{rot})
∂t∂u=HLR[x,SFRθ(ρgasLR,ρstarsLR,wrotLR))
\frac{\partial \mathbf{u}}{\partial t} = \mathcal{H}_\mathrm{LR}[\mathbf{x}, \mathrm{SFR}_{\theta}(\rho^\mathrm{LR}_\mathrm{gas},\rho^\mathrm{LR}_\mathrm{stars}, w^\mathrm{LR}_\mathrm{rot}) )
Solution: train on the fly
∂θ∂L(θ)=∂u∂L⋅∂t∂u⋅∂θ∂H[x,Rθ(x)]
\frac{\partial \mathcal{L}(\theta)}{\partial \theta} = \frac{\partial \mathcal{L}}{\partial \mathbf{u}} \cdot \frac{\partial \mathbf{u}}{\partial t} \cdot \frac{\partial \mathcal{H}[\mathbf{x}, \mathbf{R}_{\theta}(\mathbf{x})]}{\partial \theta}
L(θ)=E[∥SFRpred(θ)−SFRHR∥2]
\mathcal{L}(\theta) = \mathbb{E} \left[ \left\| \mathrm{SFR}_{\text{pred}}(\theta) - \mathrm{SFR}_{\text{HR}} \right\|^2 \right]
2. Data-driven subgrid models learned subgrid models from high dimensional observations
∂t∂u=H[x,Rθ(x)]
\frac{\partial \mathbf{u}}{\partial t} = \mathcal{H}[\mathbf{x},\mathbf{R}_{\theta}(\mathbf{x})]
Hydro simulator
Subgrid model
What is the space of plausible solutions and how do we search it?
Are these models predictive?
4. Machine learned subgrid models
[Image credit: Sarah Jeffreson's beautiful high res sims]
["Multifield Cosmology with Artificial Intelligence" Villaescusa-Navarro et al arXiv:2109.09747]
Out-of-Distribution
In-Distribution
4. Learning the feedback manifold
Representation Learning
Informative abstractions of the data
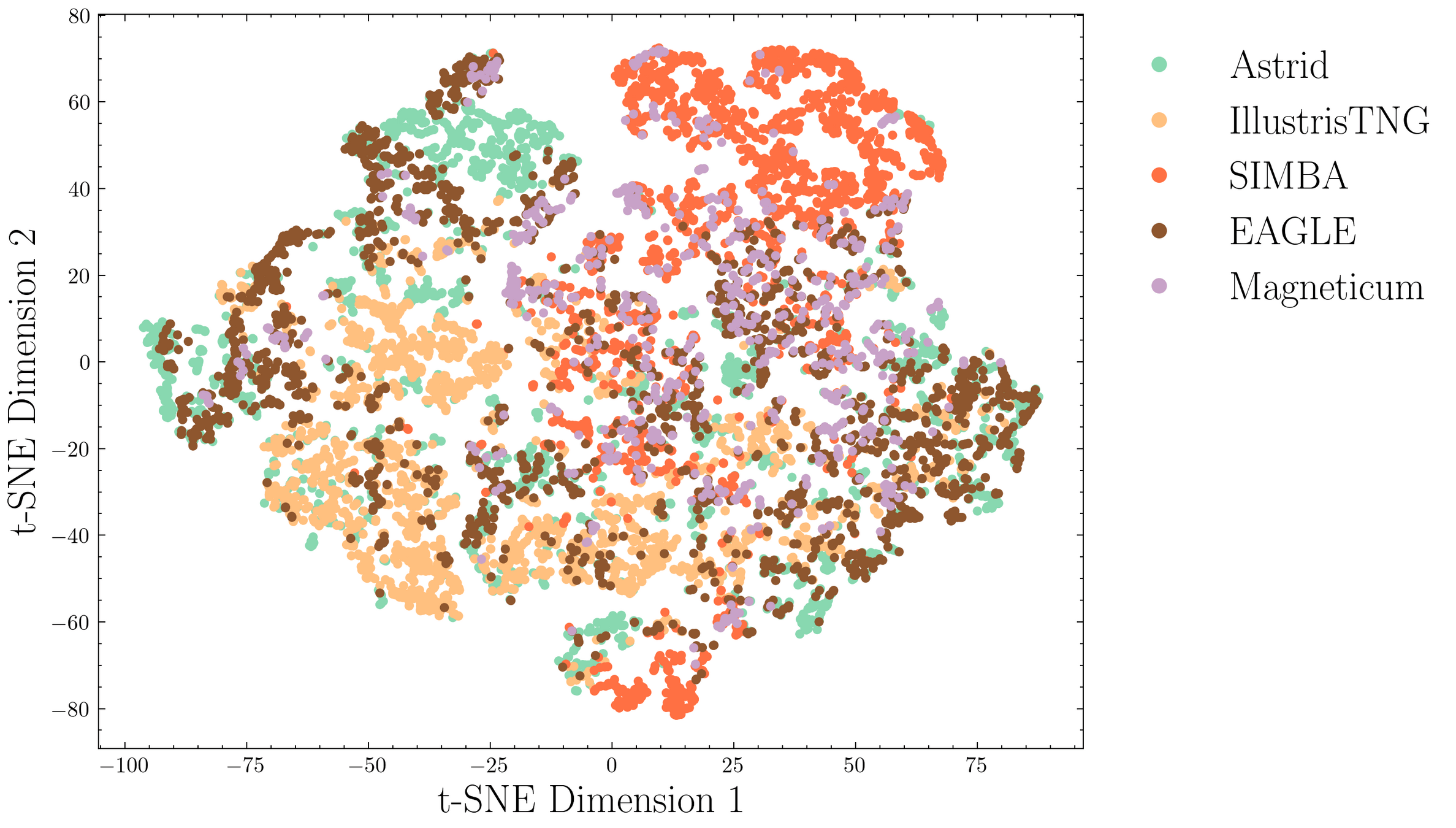
Transfer learning beyond LCDM
Cosmic web Anomaly Detection
Representing baryonic feedback
Representation Learning a la gradient descent
Contrastive
Generative
inductive biases
from scratch or from partial observations
Students at MIT are
OVER-CAFFEINATED
NERDS
SMART
ATHLETIC
Ωm,σ8
\Omega_m, \sigma_8
Simulator 1
Simulator 2
z
z
p(
p(
,z)
, z)
Dark Matter
Feedback
Ωm,σ8
\Omega_m, \sigma_8
i) Contrastive
Baryonic fields
ii) Generative
Baryonic fields
Dark Matter
Generative model
Total matter, gas temperature,
gas metalicity
p(
p(
)
)
,z)
, z)
p(
p(
z=fθ(
z = f_\theta (
)
)
Encoder
+
+
p(C,z∣
p(\mathcal{C},z|
)
)
z
z
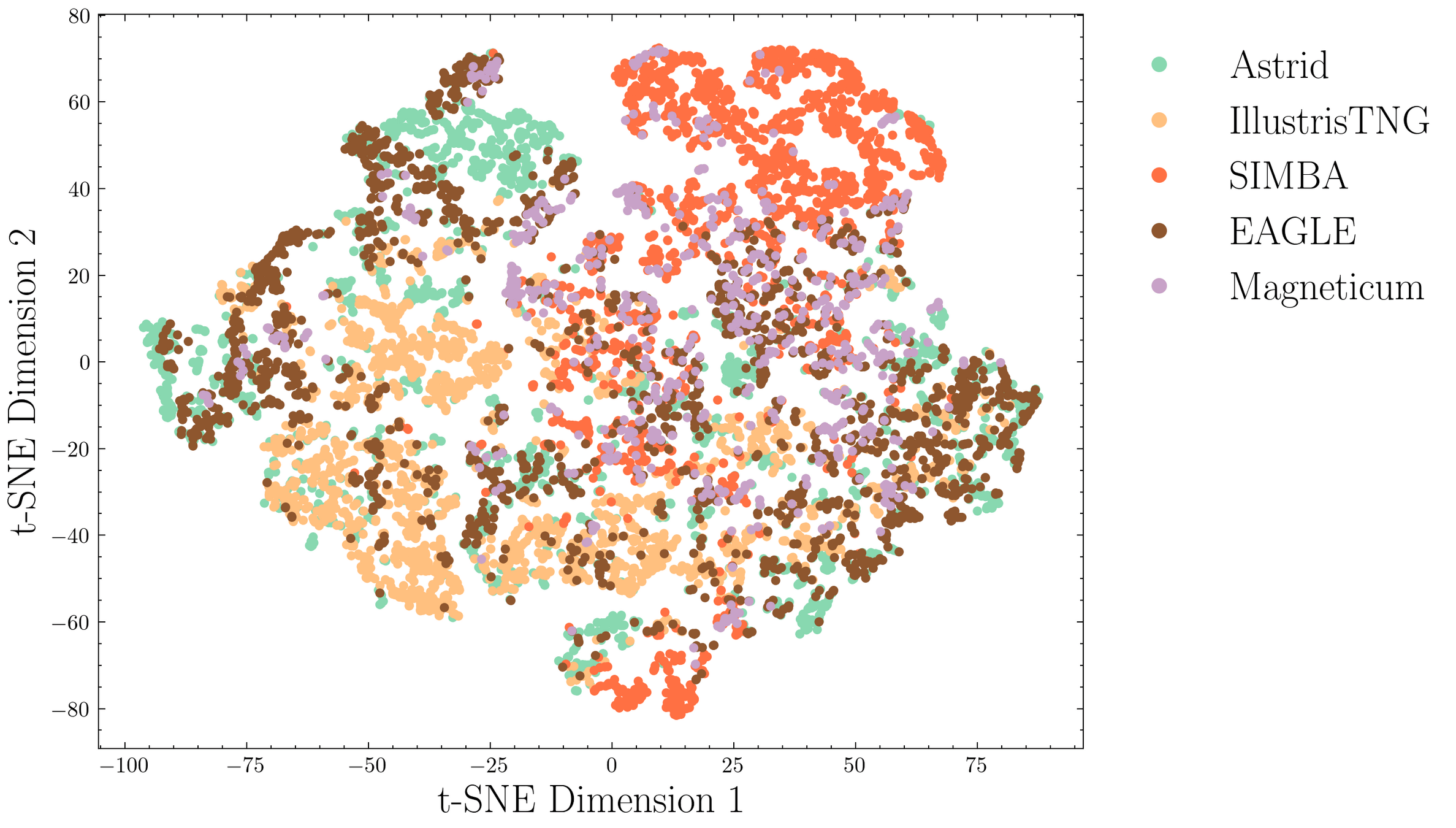
5. Compressing simulations in continuous time
~ 10 trillion particles per snapshot stored
x Discrete snapshots
(x,y,z,t)
(x,y,z,t)
Ψ,Ψ˙
\Psi, \dot \Psi
x500
x500
Generative Solutions for Cosmic Problems florpi https://florpi.github.io/ IAIFI Fellow Carol(ina) Cuesta-Lazaro
Generative Solutions for Cosmic Problems - Lars group meeting 2024
By carol cuesta
Generative Solutions for Cosmic Problems - Lars group meeting 2024
- 207
