Big Data Cosmology meets AI
An Invitation to Backpropagate Through the Origins of the Universe
IAIFI Fellow
Carol Cuesta-Lazaro
Video Credit: N-body simulation Francisco Villaescusa-Navarro
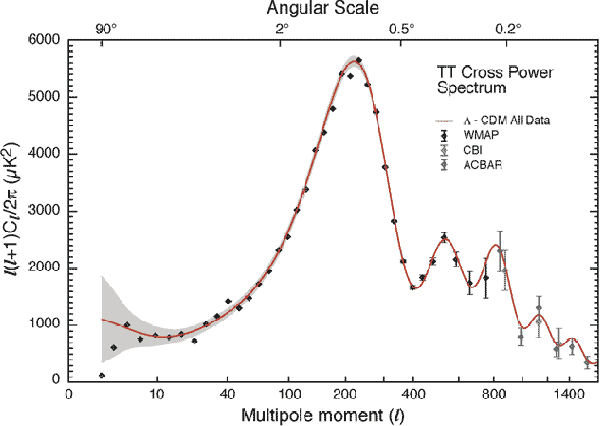
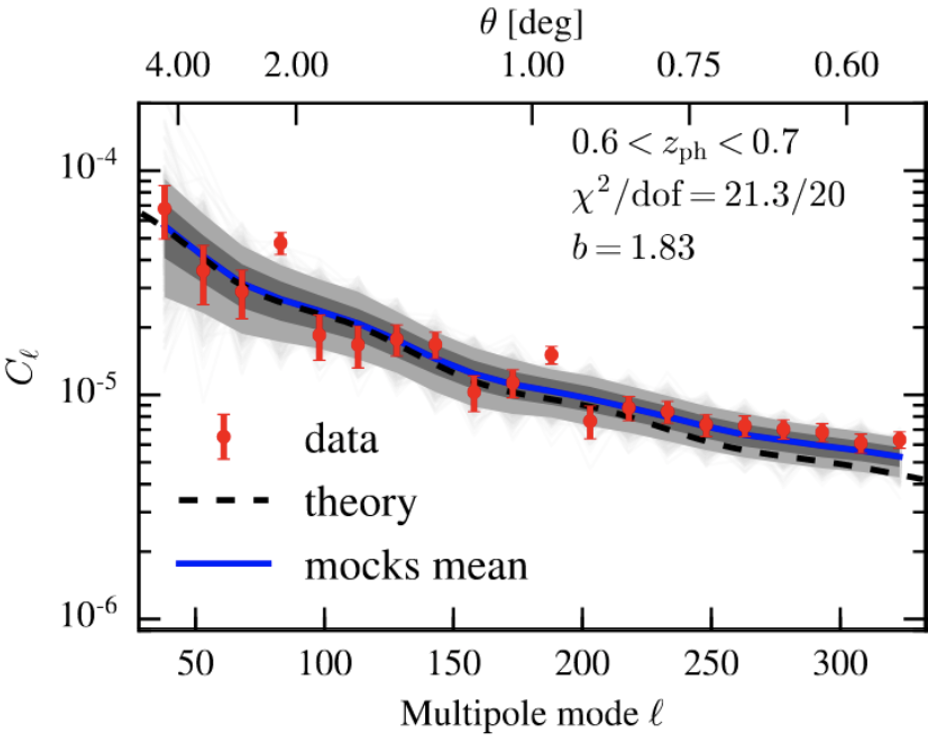
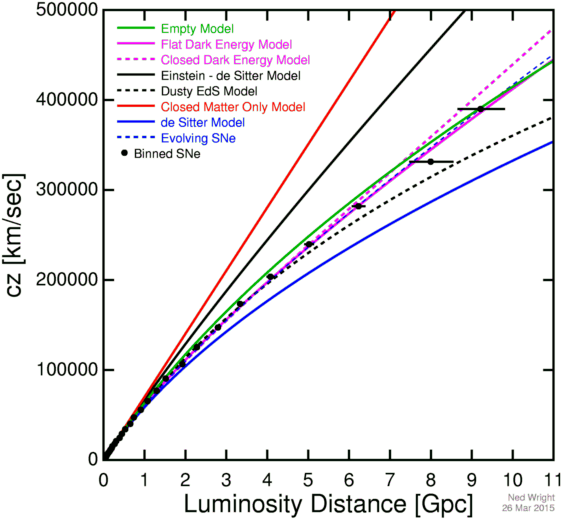
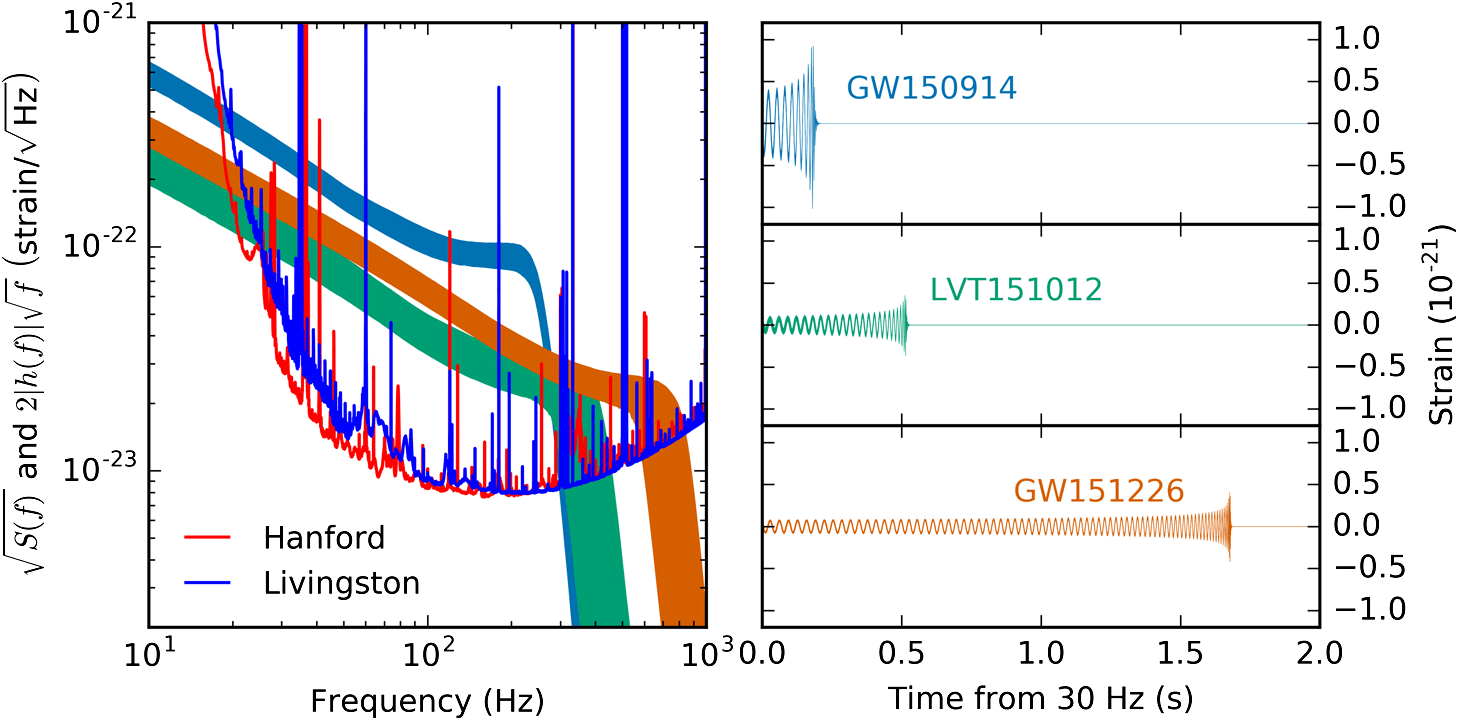
The era of Big Data Astrophysics
1-Dimensional
Machine Learning
Cosmic Cartography
Galaxy Clustering
Galaxy Imaging
Lensing
Cosmic Microwave Background
Gravitational Waves
Time domain
Early Universe Inflation
δInitial
{\delta_\mathrm{Initial}}
Late Universe
What's the Universe made of?
Evolution
δFinal
{\delta_\mathrm{Final}}
Ωm
\color{darkgray}{\Omega_m}
Dark matter
Dark energy
w0,wa
\color{darkgreen}{w_0, w_a}
fNL
\color{purple}{f_\mathrm{NL}}
Non-Gaussianity
...
Multifield Inflation
Initial Conditions
The Universe's forward model
Observables
Why Astrophysics is hard 101
Dataset Size = 1
Can't poke it in the lab
Simulations
Bayesian statistics
How well can we simulate the Universe?
Very interested on ideas in the area of model mispecification!
How do we learn what is the robust information?
Simulating dark matter is easy!
"Atoms" are hard" :(
2
2
3
3
Hybrid ML - Physics Simulators
Unsupervised searches
1
1
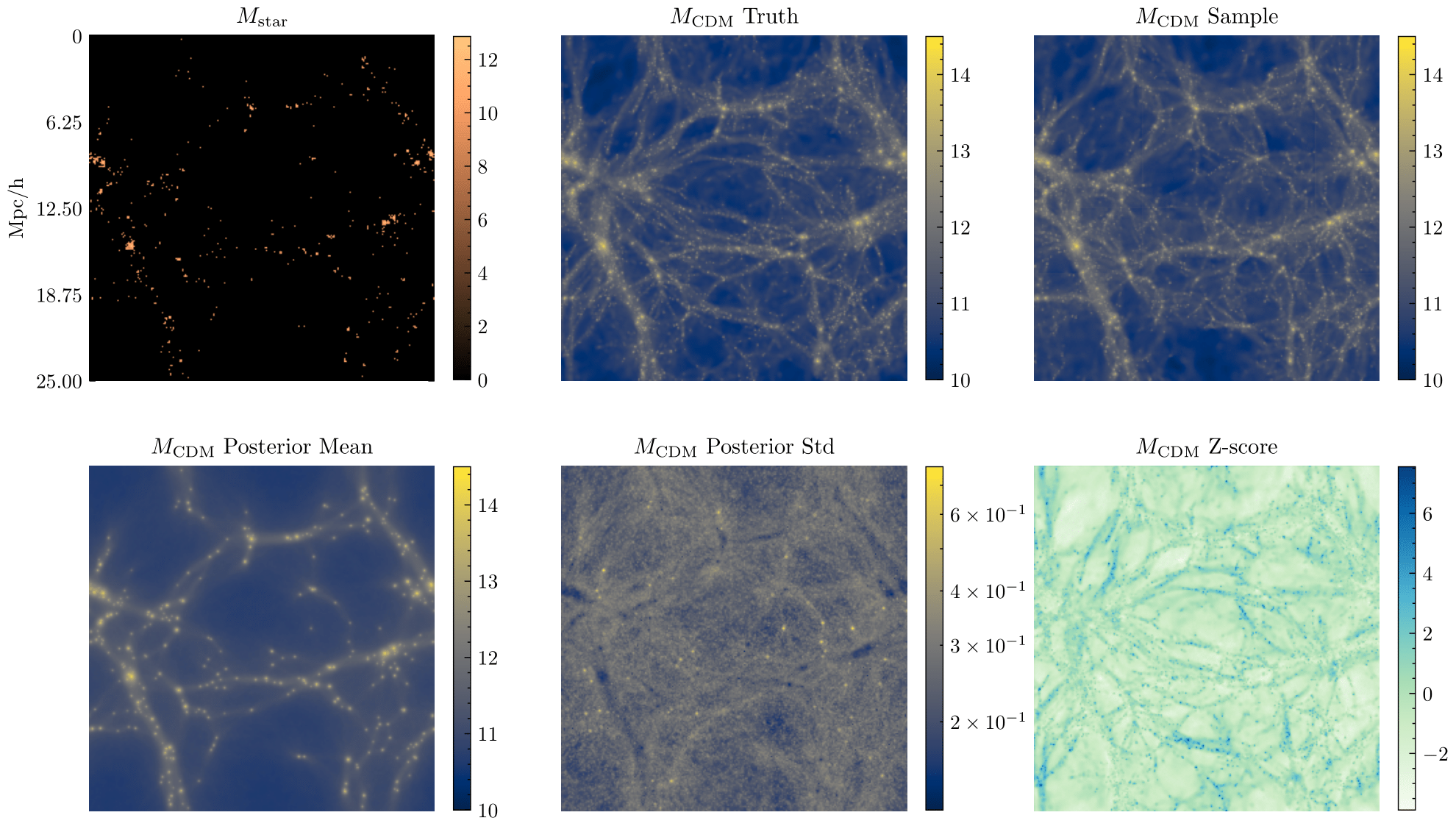
Cosmological (field level) Inference for Galaxy Surveys
DESI
High dimensional data
x
x
Unknown
p(x∣C)
p(x|\mathcal{C})
Simple summary statistic
s
s
p(s∣C)
p(s|\mathcal{C})
estimated with Perturbation Theory
Probability pair of galaxy
Pair separation
θ
\theta
Forward Model
Parameters
Observable
x
x
Likelihood
p(θ∣x)
p(\mathcal{\theta}|x)
Simulator
+ MCMC hammer
Ωm,w0,wa,fNL...
\color{darkgray}{\Omega_m}, \color{darkgreen}{w_0, w_a},\color{purple}{f_\mathrm{NL}}\, ...
Dark matter
Dark energy
Inflation
Perturbation Theory
Pen and paper
p(x∣θ)
p(x|\mathcal{\theta})
+ Density Estimation
+ Sampler
p(θ∣x)=
p(\mathcal{\theta}|x) =
p(θ)/p(x)
p(\theta) / p(x)
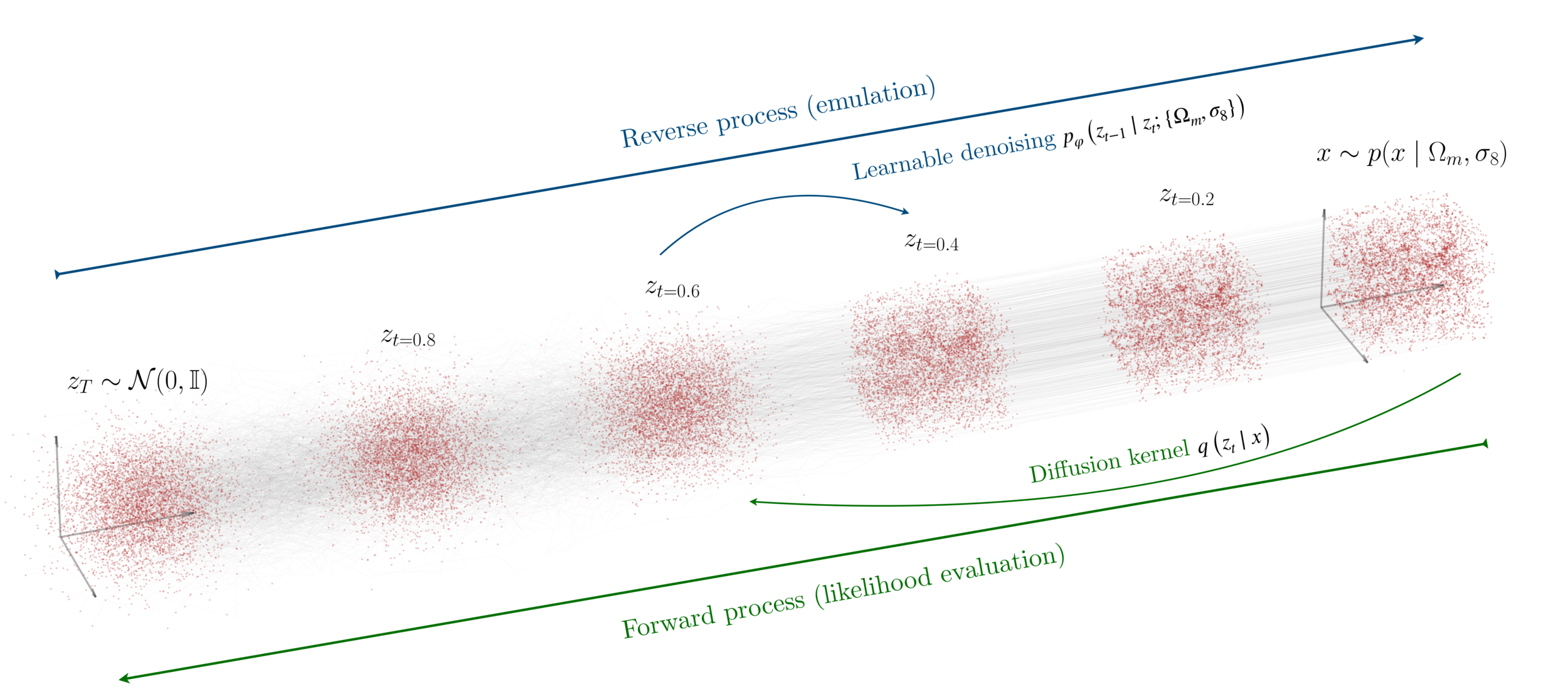
"A point cloud approach to generative modeling for galaxy surveys at the field level"
Cuesta-Lazaro and Mishra-Sharma
arXiv:2311.17141
Base Distribution
Target Distribution
- Sample
- Evaluate
Siddharth Mishra-Sharma
Long range correlations
Huge pointclouds (20M)
Homogeneity and isotropy
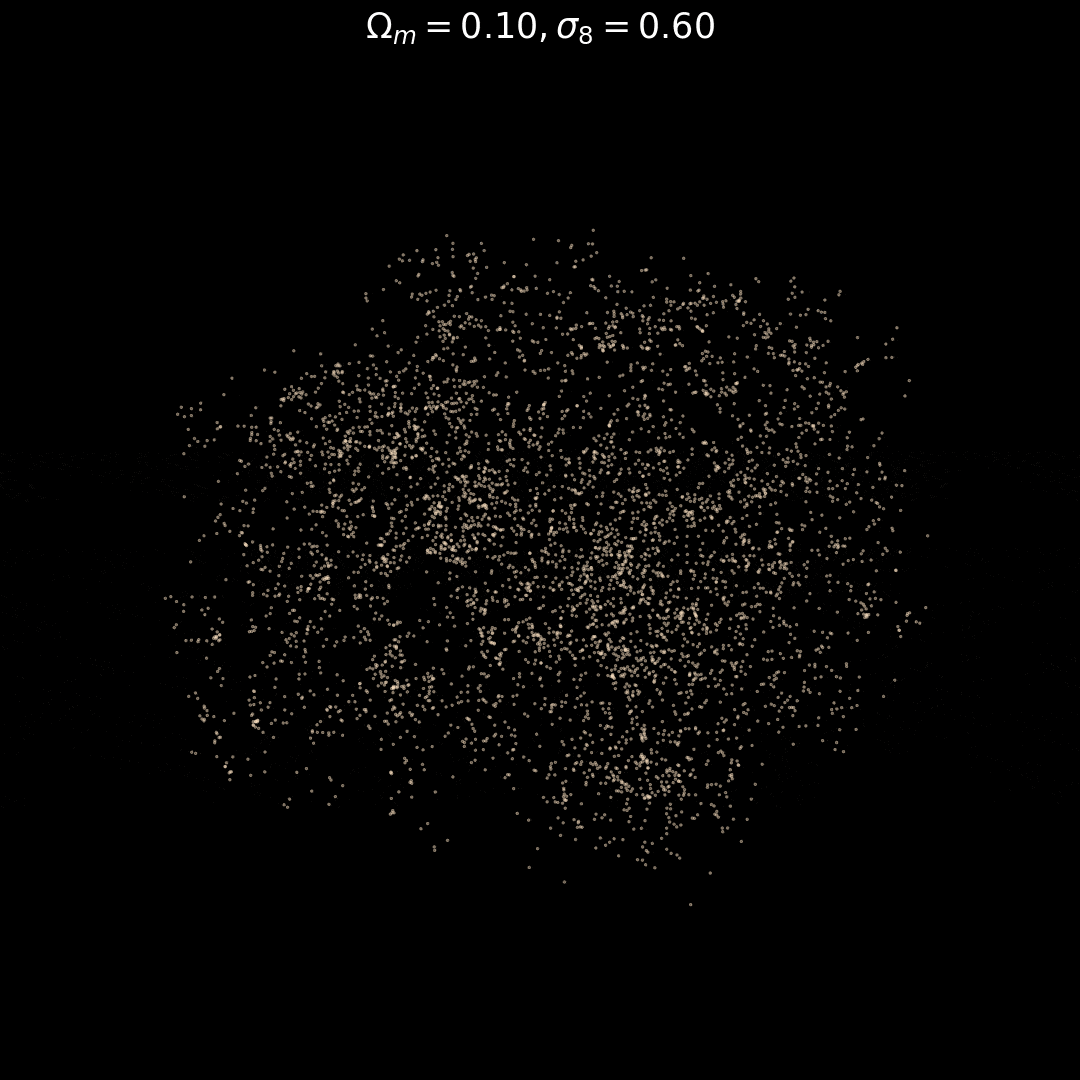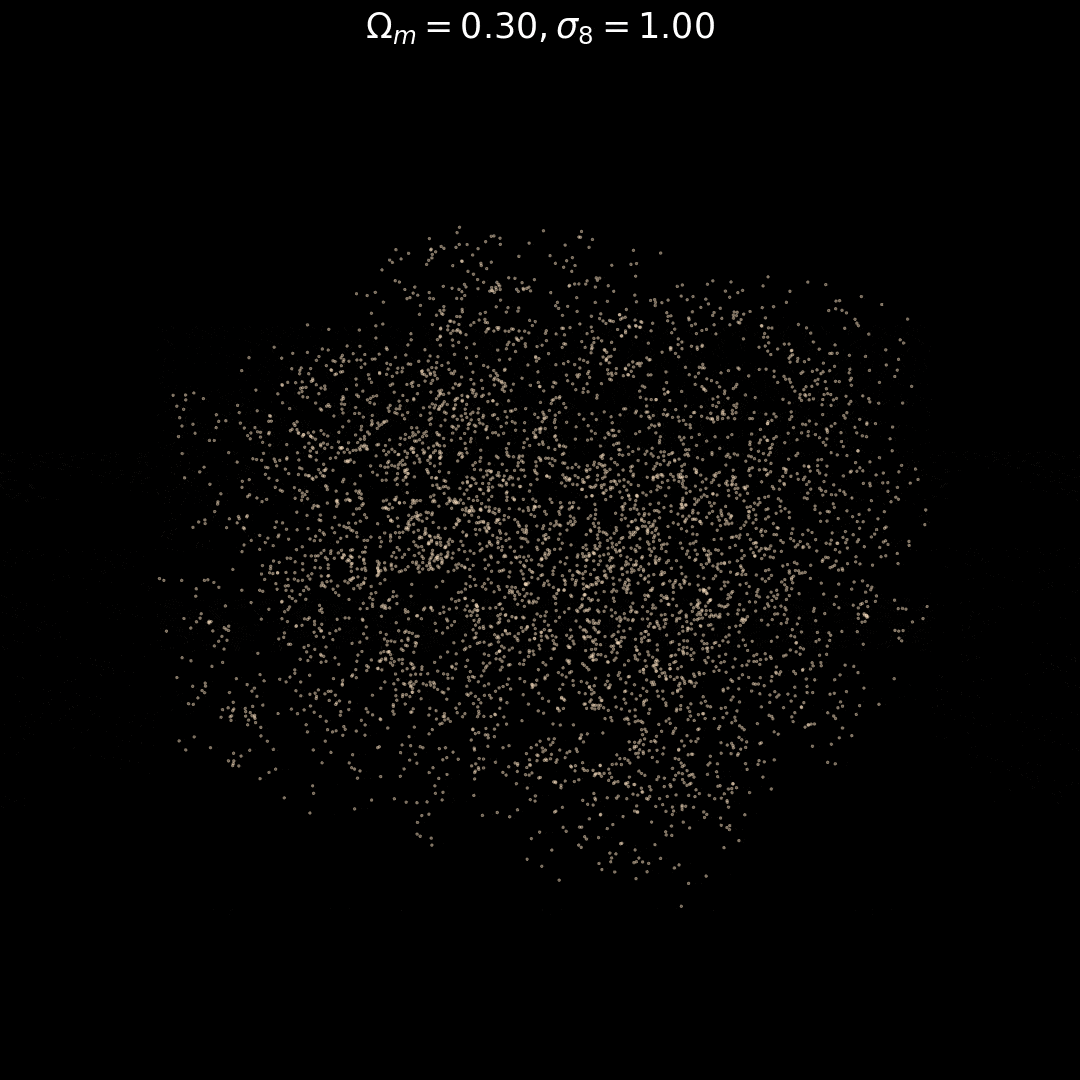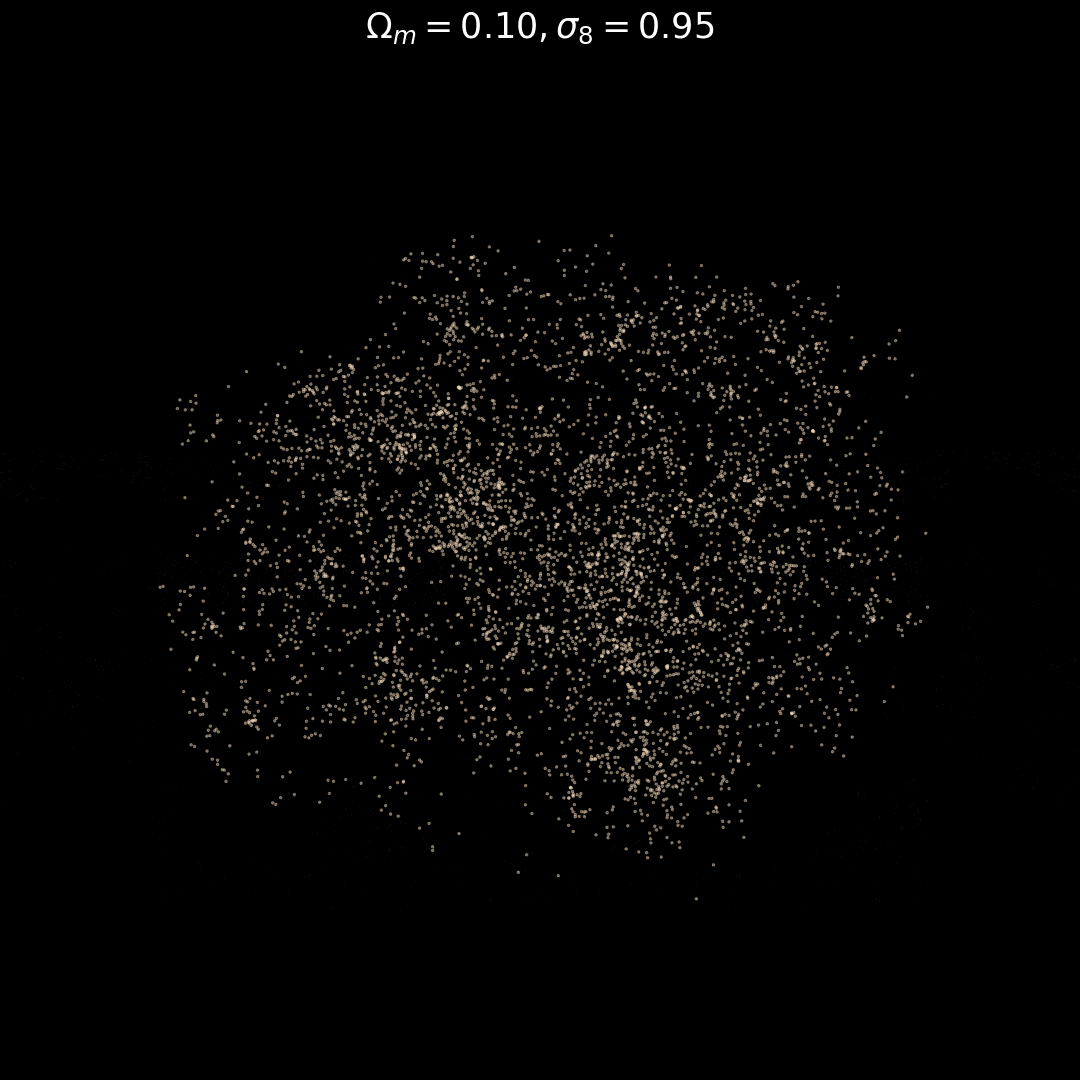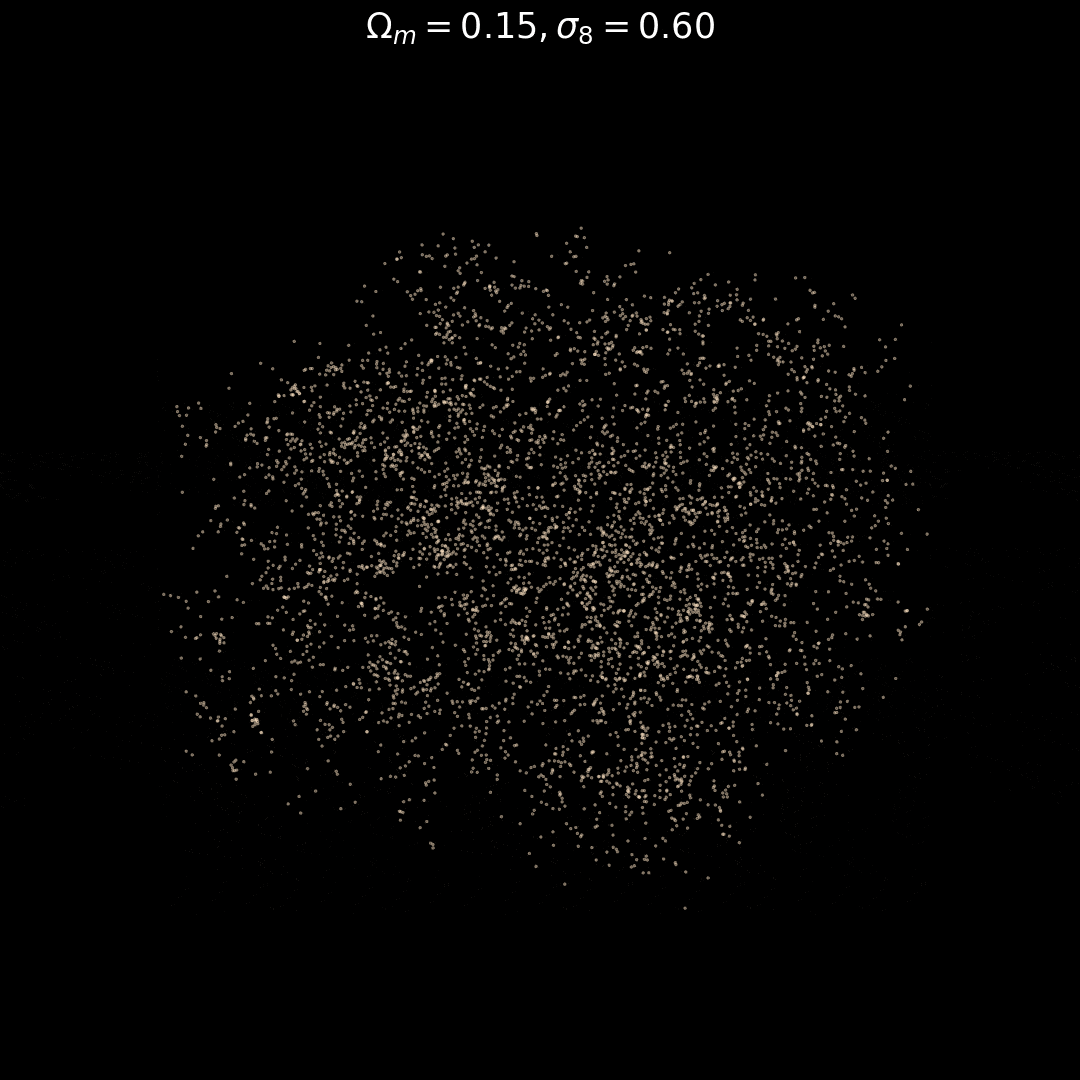
Fixed Initial Conditions
Varying Cosmology
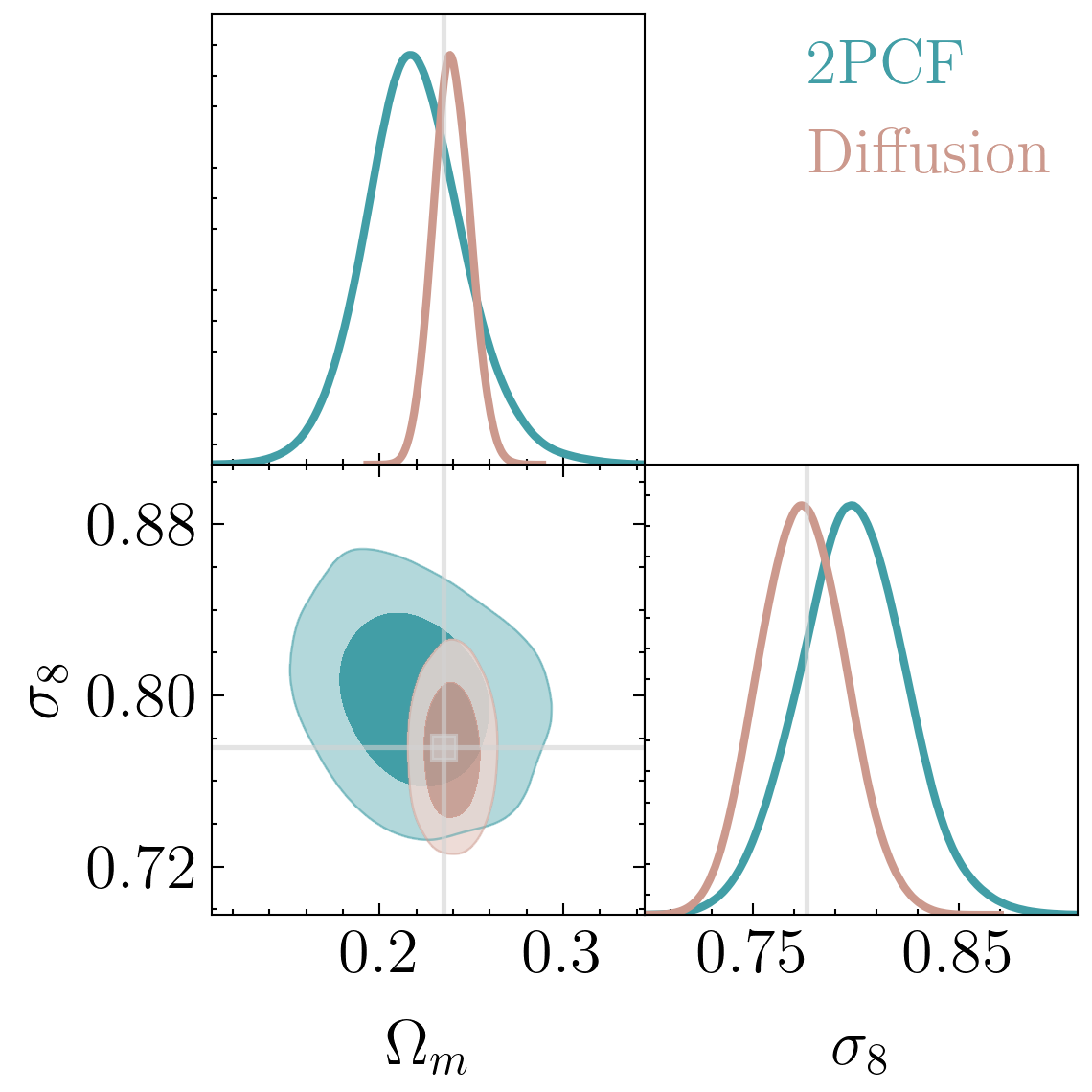
Trained on only 5000 positions!
Real observations 20 Million points :(
Learning in 5000 dimensions with only 2000 simulations
Symmetries?
Julia Balla
Loss
Step
Pair counting
MP GNN
Hierarchical
Symmetries
"GalaxyBench: A Long- and Short-Range Benchmark for Symmetry-Preserving Data Processing" Balla et al (in prep.)pϕ(δICs∣δToday)
p_\phi(\delta_\mathrm{ICs}|\delta_\mathrm{Today})
1 to Many:
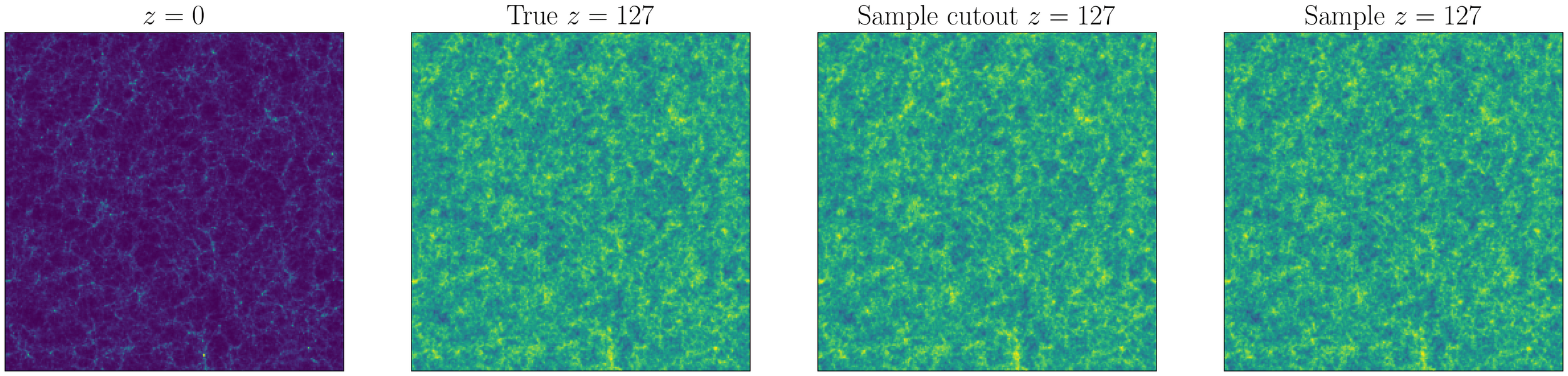
Can we run the Universe backwards?
Today
Initial Conditions
"Probabilistic Forecasting with Stochastic Interpolants and Follmer Processes" Chen et al
arXiv:2403.13724
xt=αtx0+βtx1+σtWt
x_t = \alpha_t x_0 + \beta_t x_1 + \sigma_t W_t
dXt=bt(Xt,x0)dt+σtdWt
d X_t = b_t(X_t,x_0) dt + \sigma_t dW_t
Sampling SDE
Interpolant
L=∫01E[∣b^t(xt,x0)−Rt∣2]
\mathcal{L} = \int_0^1 \mathbb{E} \left[|\hat{b}_t(x_t, x_0) - R_t|^2 \right]
Rt=αt˙x0+βt˙x1+σt˙Wt
R_t = \dot{\alpha_t} x_0 + \dot{\beta_t} x_1 + \dot{\sigma_t}W_t
x1∼p(x1∣x0)
x_1 \sim p(x_1|x_0)
Drift
Regression loss
"Probabilistic Forecasting with Stochastic Interpolants and Follmer Processes" Chen et al
arXiv:2403.13724
Current model is not very good when ran forwards!
3D U-Nets are annoying :(
True
Initial
Final
Predicted
Can we run larger simulations? (Observable volumes)
At high resolution?
Faster?
All this works depends on simulations, but...
Thousands of them?
Hybrid Physical / ML simulators
dadx=a3E(a)1v
\frac{\mathrm{d} \mathbf{x}}{\mathrm{d} a } = \frac{1}{a^3 E(a)}\mathbf{v}
dadv=a2E(a)1F(x,a)
\frac{\mathrm{d} \mathbf{v}}{\mathrm{d} a } = \frac{1}{a^2 E(a)}\mathbf{F}(\mathbf{x},a)
F(x,a)=23Ωm∇ϕPM(x)
\mathbf{F}(\mathbf{x},a) = \frac{3 \Omega_m}{2} \nabla \phi^\mathrm{PM}(\mathbf{x})
Gravitational evolution ODE
Particle-mesh
"Nbodyify: Adaptive mesh corrections for PM simulations" Cuesta-Lazaro, Modi in preps
Particle-mesh
Full Nbody
Fθ(x,a)=23Ωm∇[ϕPM(x)+ϕθcorr(x,a,ϕPM,δPM)]
\mathbf{F}_\theta(\mathbf{x},a) = \frac{3 \Omega_m}{2} \nabla \left[\phi^\mathrm{PM}(\mathbf{x}) + \phi^\mathrm{corr}_\theta(\mathbf{x}, a, \phi^\mathrm{PM}, \delta^\mathrm{PM}) \right]
Hybrid Simulator - on the fly
dadx=a3E(a)1v
\frac{\mathrm{d} \mathbf{x}}{\mathrm{d} a } = \frac{1}{a^3 E(a)}\mathbf{v}
dadv=a2E(a)1F(x,a)
\frac{\mathrm{d} \mathbf{v}}{\mathrm{d} a } = \frac{1}{a^2 E(a)}\mathbf{F}(\mathbf{x},a)
Gravitational evolution ODE
Trained to match particle velocities and positions: DIFFERENTIABLE
L=t∑(xtpred−xtHR)2
\mathcal{L} = \sum_t \left(x_t^{\rm pred} - x_t^{\rm HR}\right)^2
δLR
\delta_\mathrm{LR}
ϕLR
\phi_\mathrm{LR}
Density
Gravitational Potential
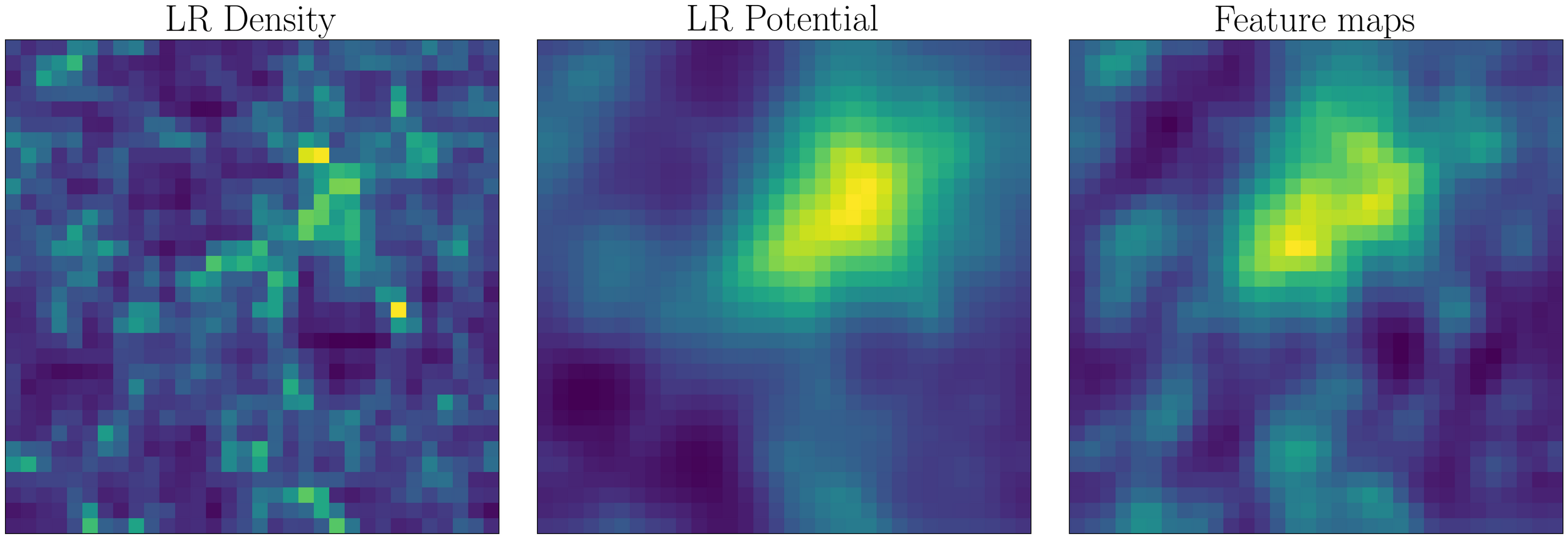
1. CNN
2. Read features at position using attention
Fθ(x,a)=fθ(hθ(x),a)
\mathbf{F}_\theta(\mathbf{x},a) = f_\theta(h_\theta(\mathbf{x}), a)
3. Compute force correction
4. Run corrected simulation
Learn features
hθ(x)
h_\theta(\mathbf{x})
h
h
Particle-mesh
Full Nbody
Hybrid ML-Simulator
"Nbodyify: Adaptive mesh corrections for PM simulations" Cuesta-Lazaro, Modi in prepsVideo credit: Francisco Villaescusa-Navarro
Gas density
Gas temperature
Finding missing physics with differentiable simulators?
What is the space of plausible solutions and how do we search it?
Differentiable Galaxies ODEs
Humans best bet
dtdGalaxies=ϕ(DarkMatter(t))
\frac{d \mathrm{Galaxies}}{dt} = \phi(\mathrm{Dark Matter}(t))
+ϕθ(?)
\color{blue}{+ \phi_\theta(?)}
Neural Network correction
Are there problems in cosmology that bypass a forward model?
Parity violation cannot be originated by gravity
7σ
7 \sigma
x
x
Mirror(x)
\mathrm{Mirror}(x)
"Measurements of parity-odd modes in the large-scale 4-point function of SDSS..." Hou, Slepian, Chan arXiv:2206.03625
?
?
1σ
1 \sigma
"Could sample variance be responsible for the parity-violating signal seen in the BOSS galaxy survey?" Philcox, Ereza arXiv:2401.09523
x
x
Mirror(x)
\mathrm{Mirror}(x)
max(fθ(x)−fθ(Mirror(x)))
\mathrm{max} \, \left( f_\theta(x) - f_\theta(\mathrm{Mirror}(x)) \right)
Train
Test
Me: I can't wait to work with observations
Me working with observations:
Finding interesting objects:
Very small galaxies (dwarf galaxies)
Interesting in Astrophysics: How we define an anomaly and how do we find it?
Background
Region of Interest
pBckG(xstar)pRoI(xstar)
\frac{p_\mathrm{RoI}(x_\mathrm{star})}{p_\mathrm{BckG}(x_\mathrm{star})}
Conclusions
1. There is a lot of information in galaxy surveys that ML methods can access
2. We can tackle high dimensional inference problems so far unatainable
3. Our ability to simulate will limit the amount of information we can extract
Hybrid simulators, forward models, robustness
Unsupervised problems: parity violation
Finding anomalies for new physics?
Finding the Initial Conditions of the Universe, let's get creative!
Field level inference
Big Data Cosmology meets AI An Invitation to Backpropagate Through the Origins of the Universe IAIFI Fellow Carol Cuesta-Lazaro Video Credit: N-body simulation Francisco Villaescusa-Navarro
MIT-CTPSeminar2024
By carol cuesta
MIT-CTPSeminar2024
- 318
