Corentin Cadiou\({}^{1,2}\)
Oscar Agertz\({}^{1}\)
Santi Roca-Fàbrega\({}^{1}\)
\({}^1\)Division of astrophysics, Department of physics, Faculty of Science, Lund University
\({}^2\)Institut d’Astrophysique de Paris, CNRS, France

Galaxy formation in the exascale era


Cosmological simulations
Self-consistent formation of galaxies
Initial conditions
Simulated galaxies
-
understand:
What's needed to reproduce observations? -
explain:
How do galaxies form? -
predict:
Future observations?
NASA

\(<1\,\%\)
Exponentially-expanding Universe

Dark matter
Gas (H+He)
Stars
Orders of magnitude
The simulation challenge
Time
Universe: \(13.7\,\mathrm{Gyr}\)
Supernova: \(1\,\mathrm{kyr}\)
⇒ \(10^7\) steps/simulation
NASA/CXC/A.Jubett
Mass
\(10^{11}\,M_\odot\): Milky-Way
\(1\,M_\odot\): typical star
⇒ \(10^{11}\) particles
Resolution:
\(\sim 10^{6}\,\mathrm{ly}\): cosmological env.
\(\sim 1\,\mathrm{ly}\): supernova scale
⇒ \(>6\) orders of magnitude resolution
⇒ \(10^{18}\) updates
\(230\,\mathrm{yr}\) on my laptop's CPU
\(18\,\mathrm{yr}\) on my GPU
\(11\,\mathrm{month}\) on an NVIDIA H100

Orders of magnitude
of existing code (RAMSES) / Vintergatan simulation
Took:
- 4 MCPU.hr on 1500 cores (\(490\,\mathrm{yr}\))
- \(10^8\) particles + \(3\times10^{8}\) cells (\(M=10^3\,\mathrm{M_\odot}\))
- \(67\,\mathrm{GiB}\) of data/output, 200 outputs
- Would take the same time on… 6 H100 GPUs
RAMSES: Teyssier 2003
Vintergatan: Cadiou in prep, Agertz+21
Efficiency: green top 500
DM
gas
star
\(\sim 30-70\,\mathrm{Gflop/W}\)
\(\sim 5-50\,\mathrm{Gflop/W}\)
\(\sim2\,\mathrm{tCO_{2,eq}}\)
\(<1\,\mathrm{tCO_{2,eq}}\)?

Data: Top-500

Dyablo Simulation Code
Manage grid, simple computation
Computation-heavy
(hydro, gravity, …)
CPU
GPU
[…]
wasted
time
wasted
time
Typical approach: offloading
Dyablo's approach:
Amdahl's law: latency kills gains of parallelisation
Dyablo Simulation Code
Manage grid, simple computation
Computation-heavy
(hydro, gravity, …)
CPU
GPU
(or CPUs)
[…]
Typical approach: offloading
Dyablo's approach: “true” GPU computing, CPU as a puppeteer
Main developers: P. Kestener, A. Durocher, M. Delorme (CEA)
+ GINEA collaboration (ObAS, IAP, CRAL, CRIStAL …)
Dyablo: how does it scale?
Image credits: Arnaud Durocher
Remember the 6 GPUs equivalent to 1500 CPUs?

Scaling test with replicated explosions (one per process)
\(80\times\) more operations
No gravity, no galaxy physics, no dark matter, no expansion of the Universe, …
dyablo: a (very) promising code
But all the physics is missing and
important bottlenecks remain
Bottleneck1: communications
CPU#1
CPU#2
CPUs: Computation-dominated
Exemple: solving gravity with conjugate gradient
\[{\color{cyan}\Delta} {\color{lime}\phi} = {\color{gray}4\pi G} {\color{salmon}\rho} \quad\Leftrightarrow\quad {\color{cyan}\textbf{A}} {\color{lime}x} = {\color{salmon}b} \]
Bottleneck1: communications
GPU#1
GPU#2
GPUs: Communication-dominated
Exemple: solving gravity with conjugate gradient
\[{\color{cyan}\Delta} {\color{lime}\phi} = {\color{gray}4\pi G} {\color{salmon}\rho} \quad\Leftrightarrow\quad {\color{cyan}\textbf{A}} {\color{lime}x} = {\color{salmon}b} \]
Bottleneck1: communications
GPU#1
GPU#2
GPUs: Communication-dominated
Ligo collaboration
In reality:
gravity propagates at speed of light
Exemple: solving gravity with conjugate gradient
\[{\color{cyan}\Delta} {\color{lime}\phi} = {\color{gray}4\pi G} {\color{salmon}\rho} \quad\Leftrightarrow\quad {\color{cyan}\textbf{A}} {\color{lime}x} = {\color{salmon}b} \]
Bottleneck1: communications
GPU#1
GPU#2
GPUs: Communication-dominated
GPU#1
GPU#2
Work package 1: Propagate gravity from cell-to-cell
few global communications, more costly*
*cost is limited in galaxy formation models where timestep is already small
Bottleneck2: Reduce communicated data




Bottleneck2: Reduce communicated data
Bottleneck2: Reduce communicated data


Hilbert curve partitioning:
- optimal workload
- large boundaries
Best for computation-dominated
Work package 2: Use Voronoi tesselation for load-balancing

- minimal boundaries
- ~good workload
Best for communication-dominated

Bottleneck2: Reduce communicated data
\[\dfrac{\mathrm{d} X_i}{\mathrm{d} \tau} \propto \text{workload gradient}\]
First test in post-processing:
-40% cells at boundary

Work package 2: Use Voronoi tesselation for load-balancing

- minimal boundaries
- ~good workload
Best for communication-dominated



\(\mathrm{age}>10\,\mathrm{Myr}\)
skip particle
\(\mathrm{age}=10\,\mathrm{Myr}\)
supernova
\(\mathrm{age}<10\,\mathrm{Myr}\)
winds
Practical exemple: star explosions (simplified)
Bottleneck3: Warp divergences
Bottleneck3: Warp divergences
\(\mathrm{age}>10\,\mathrm{Myr}\)
skip particle
\(\mathrm{age}=10\,\mathrm{Myr}\)
supernova
\(\mathrm{age}<10\,\mathrm{Myr}\)
winds
Practical exemple: star explosions
if (age < 10) { // Winds
A;
B;
C;
} else if (age == 10) { // SN
D;
E;
F;
} else {
G;
}Time
GPU “warp” (N threads)
inactive
inactive
in.
inactive
Bottleneck4: Limited GPU memory
| AMD EPYC 7413 | 128 GiB | 24 cores | 5 GiB/unit |
| NVIDIA A40 | 48 GiB | 10,000 comp. units | 4.8 MiB/unit |
Exemple on Cosmos (Lund's cluster):
Bottleneck4: Limited GPU memory
| AMD EPYC 7413 | 128 GiB | 24 cores | 5 GiB/unit |
| NVIDIA A40 | 48 GiB | 10,000 comp. units | 4.8 MiB/unit |
Exemple on Cosmos (Lund's cluster):

Log density
Bottleneck4: Limited GPU memory
| AMD EPYC 7413 | 128 GiB | 24 cores | 5 GiB/unit |
| NVIDIA A40 | 48 GiB | 10,000 comp. units | 4.8 MiB/unit |
Exemple on Cosmos (Lund's cluster):

1.0001
0.9998
0.9999
1.0002
Log density
Bottleneck4: Limited GPU memory
1.0001
0.9998
0.9999
1.0002
Work package 4: On-the-fly compression
Raw data
Update
Compressed data
Decompress
Compress
Raw data
Compressed data
1.0000
4
Mean
Common bits
+2
-2
-1
+1
Example: \(\Delta\) encoding
Requirements:
- local
- parallel
- fast
First test in post-processing: -30% compression
Bottleneck4: Limited GPU memory
First test in post-processing:
-30% compression
Compression
- Compute \(x_\mathrm{mean}\)
- \( x_i := x_i \oplus x_\mathrm{mean} \)
- Count number of leading zeros \(N_0\)
- Store \(\{x_\mathrm{mean},N_0,x_i\}\),
Decompression
\( x_i := x_i \oplus x_\mathrm{mean} \)
1.0000
4
Mean
Common bits
+2
-2
-1
+1
Work package 4: On-the-fly compression
Porting codes to GPUs:
- \(\mathrm{CO_2/sim}\) benefits,
- Huge potential performance gains,
- Practical requirement.

This project:
- Limit communications,
- Decrease amount to be communicated,
- Port physics onto GPU,
- Compress data on-the-fly.



Promising new open source code: Dyablo (github/Dyablo-HPC/Dyablo)
We thank eSSENCE for the support
\({}^1\) Astronomy @ Lund
\({}^2\) Institut d'Astrophysique de Paris, France
Corentin Cadiou\({}^{1,2}\)

Santi Roca-Fàbrega\({}^1\)

Oscar Agertz\({}^1\)

☑ Hydrodynamics
(M. Delorme, A. Durocher)
☑ Gravity
(A. Durocher, M.-A. Breton)
☑ Cosmology
(O. Marchal, D. Aubert)
Today
Spring 2025?
“Full” cosmological sim on GPU
Dyablo: status
☐ Gas cooling (CC)
☐ Star form. & feedback (incl. CC)
+ RT, MHD, testing, setting up ICs, ...




Mellier+24

Schaye+24
Sims including baryons:
\(\sim 100\times\) smaller volumes than observed
- How to beat cosmic variance?
- How to understand \(k>10\,h\,\mathrm{Mpc}^{-1}\) effects?
Part I:
(somewhat) clever solutions
Genetic Modification Method (GM)
There's a lot of freedom in the initial conditions.
\(\tilde\delta=\sum_k {\color{green} a_k} \exp(i\mathbf{k r} + {\color{red}\phi_\mathrm{k}})\)
Constraint:
\(\langle a_{\mathbf{k}} a_{\mathbf{k'}}^\dagger\rangle = P(k)\delta_\mathrm{D}(\mathbf{k}-\mathbf{k}')\)
Constraint:
\(\phi_\mathrm{k}\sim \mathcal{U}(0,2\pi)\)
a. Inverted Initial Conditions
Utilizing inverted initial conditions to enhance estimators accuracy.
Pontzen+15, see also Chartier+21, Gábor+23

\(\tilde\delta_\mathrm{S}=\sum_{k<k_\mathrm{thr}} {\color{green} a_k} \exp(i\mathbf{k r} + {\color{red}\phi_k})+\sum_{k>k_\mathrm{thr}} {\color{green} a_k} \exp(i\mathbf{k r} + {\color{red}\phi_k+\pi})\)

\( 3^{\mathrm{rd}}\)-order correction
/ up-to-\(2^{\mathrm{nd}}\)
b. Splicing Technique
Most likely field \(f\) with
- same value in spliced region (\(a\)),
- as close as possible outside (\(b\))
Mathematically, \({\color{green}f}\) is the unique solution that satisfies:
- \( {\color{green}f(x)}= {\color{blue}a(x)},\qquad\qquad\qquad\forall x \in\Gamma\)
- minimizes \[\mathcal{Q} = ({\color{red}b}-{\color{green}f})^\dagger\mathbf{C}^{-1}({\color{red}b}-{\color{green}f}),\quad \forall x \not\in \Gamma \]
CC+21a





b. Splicing Technique

Same halo, different location in the cosmic web


\(z=0\)
\(z=0\)
\(z=0\)
Storck, CC+24
b. Splicing Technique

Same halo, different location in the cosmic web

Halo mass
Intrinsic
alignment
\(\sigma\)
Storck, CC+24
b. Splicing Technique
Same halo, different location in the cosmic web

\(\sigma\)
⇒ 10-100% of I.A. signal driven by the cosmic web*
*couplings beyond standard predictions, from e.g. constrained TTT
Storck, CC+24

Std. dev / mean
Numerical noise
Population scatter
c. Angular momentum GMO
Same galaxy, different tidal enviroment
CC+21b
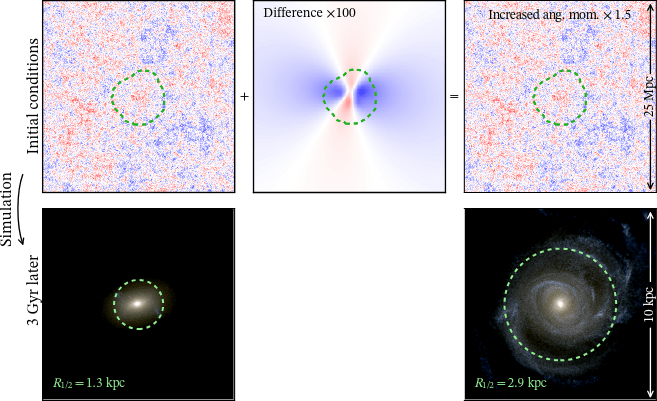
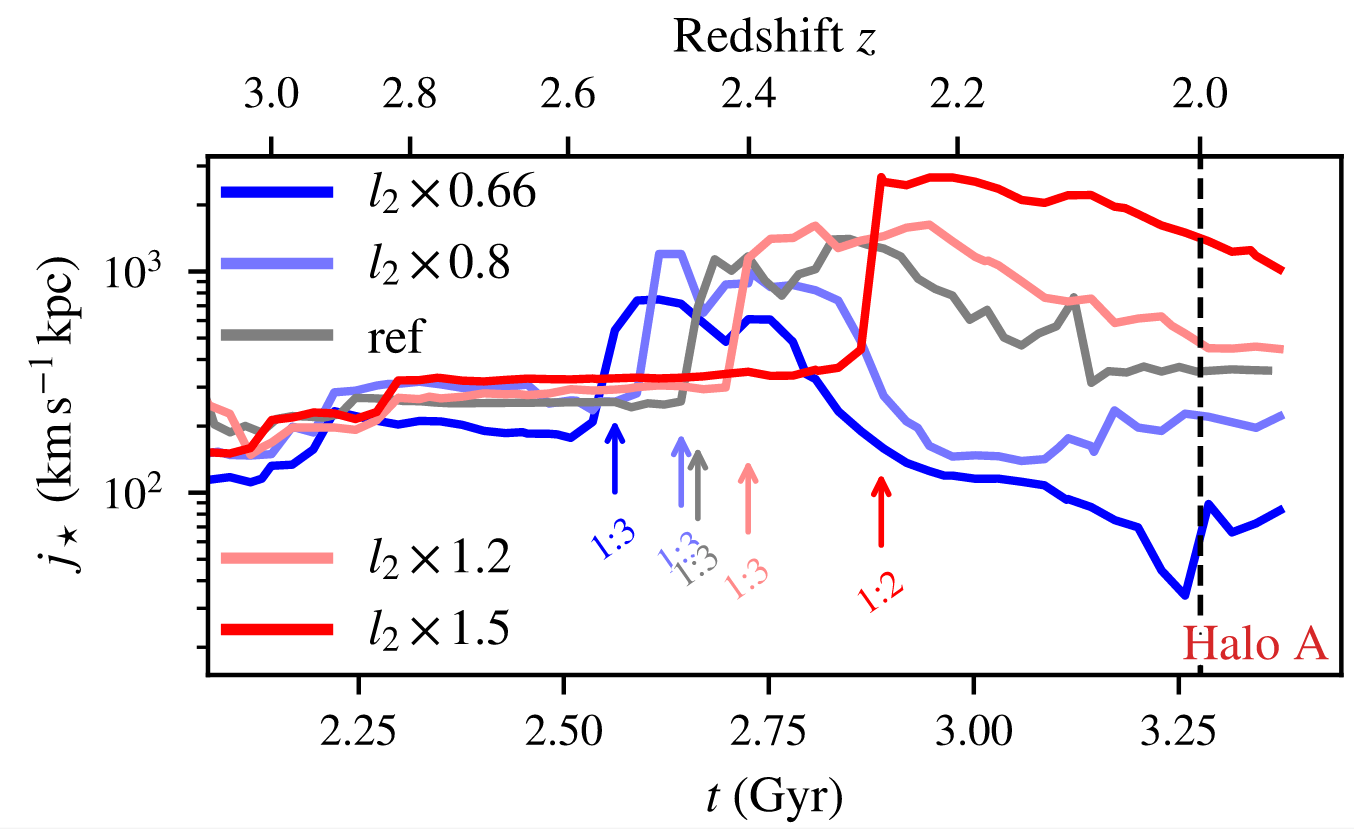
Study response at low-\(z\)
\(k>10\,h\,\mathrm{Mpc}^{-1}\)
Perturb tides at \(z\rightarrow\infty\)
on \(10-100\,h^{-1}\,\mathrm{Mpc}/h\)
LSS perturbations propagate quasi-linearly down to \(\mathrm{kpc}\) scales
⇒ Large \(k\) contain cosmological information
Part II:
bruteforce solutions
“When everything else fails, use more CPU time”
FLAMINGO (Schaye+23)
\(21\,\mathrm{Gpc}^3\), SWIFT
→ SPH approach

Large-volume hydro-cosmo simulations
State-of-the-art
Millenium-TNG (Springel+22)
\(0.125\,\mathrm{Gpc}^3\), Arepo
→ moving-mesh approach
Grid-based code?
Quite a shame, because it's where France's experts are
(Dubois, Hennebelle, Bournaud, …)
?
Conclusion & take home message
- Possible to build cosmological experiment
⇒ GMs as machine to study scale couplings- Thoughts on possible applications for DE/DM questions?
- \(10\,\mathrm{Mpc}/h\leftrightarrow \mathrm{kpc}\) for scalars (Mass, \(R_\mathrm{vir}\), ...) is small
-
from \(\sim 100\,\mathrm{Mpc}/h\) to \(\sim \mathrm{kpc}\) large for vector quantities (AM, shape)
- When clever approaches fail, resort to brute force
- Future is (most likely) driven by GPUs
- Promising developments in France with Dyablo
https://github.com/Dyablo-HPC/Dyablo
eSSENCE | Galaxy formation in the exascale era
By Corentin Cadiou
eSSENCE | Galaxy formation in the exascale era
- 237



