On the causal origin of properties of dark matter halos and galaxies



With A. Pontzen & H. Peiris: 2012.02201, 2107.03407
Corentin Cadiou | Källén Seminar @ Lund
Galaxy formation
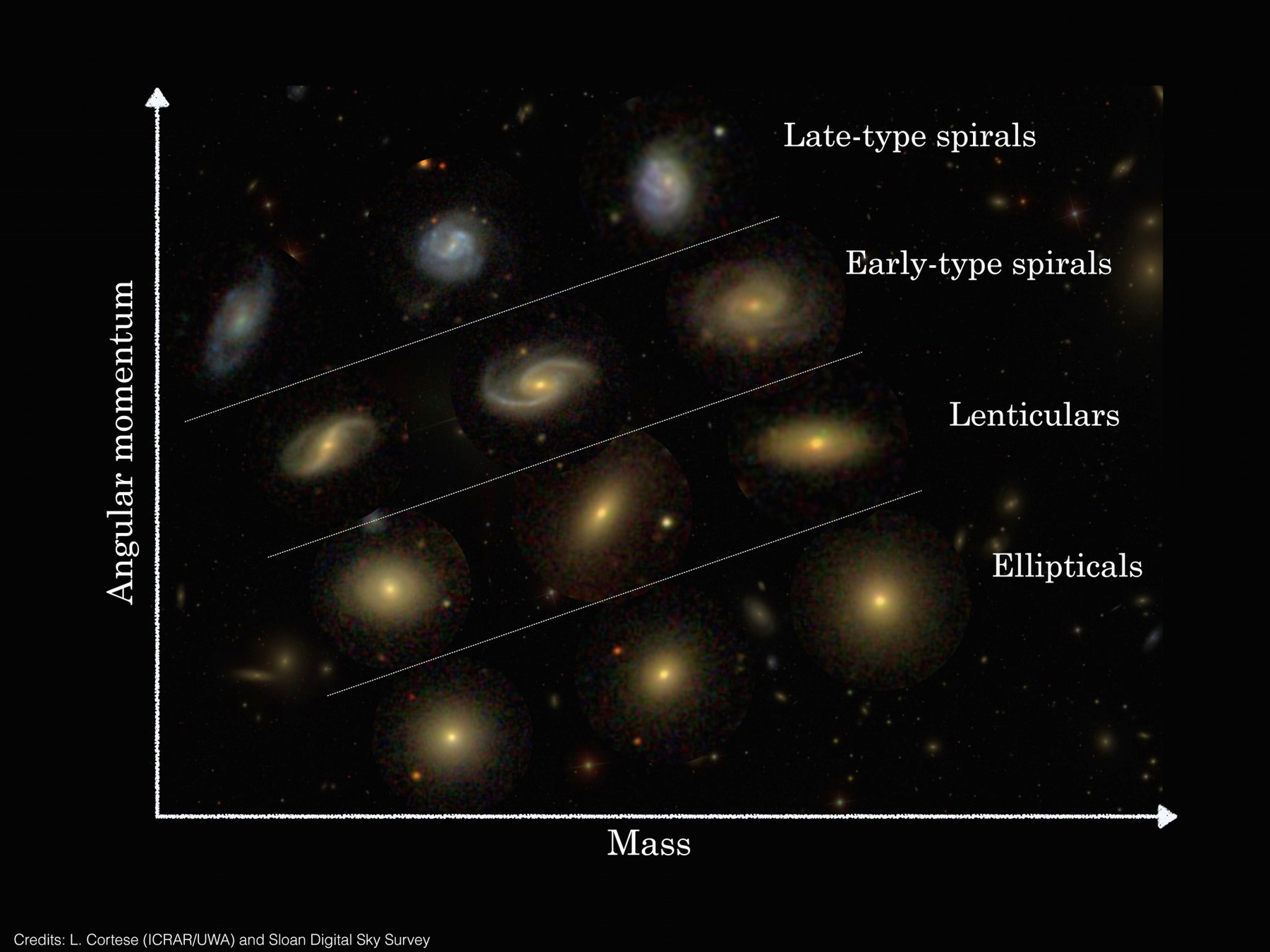
[L. Cortese; SDSS.]



[Dubois+16]
AGN no AGN
Origin of morphological diversity at fixed mass?

[L. Cortese; SDSS.]



[Dubois+16]
AGN no AGN
Origin of morphological diversity at fixed mass?
How to explain environmental effects?

Galaxy formation



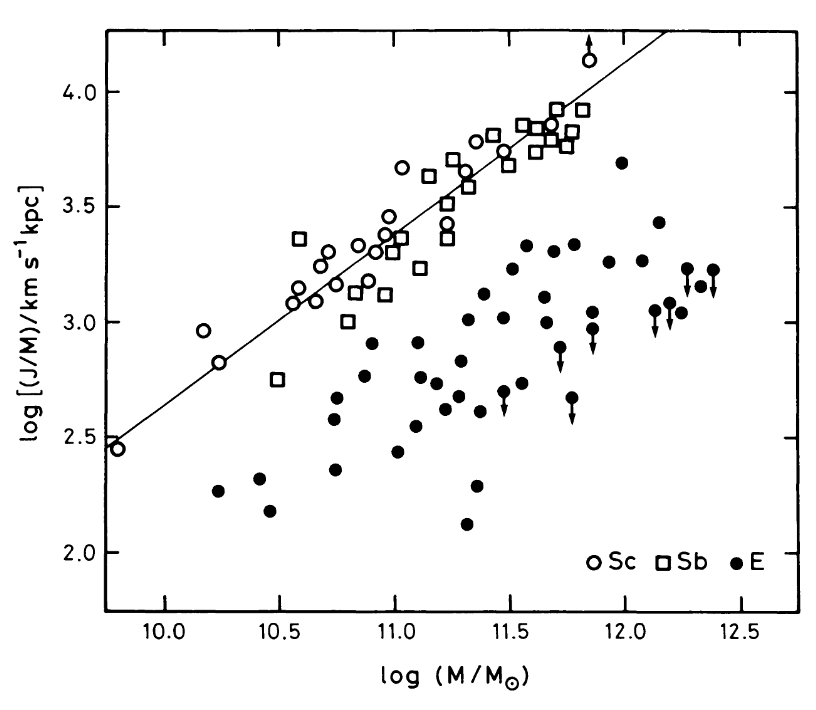
Fall 83 (\(z=0\))
Spiral galaxies \(\leftrightarrow\) high \(J_\star\)
3 variables: \(M_\star, J_\star\), morpho.
What causes what?
Some possible scenarios:
- Quench then spin down?
- Grow & spin down then quench?
- Spin down then quench
Galaxy formation in cosmology: the role of angular momentum
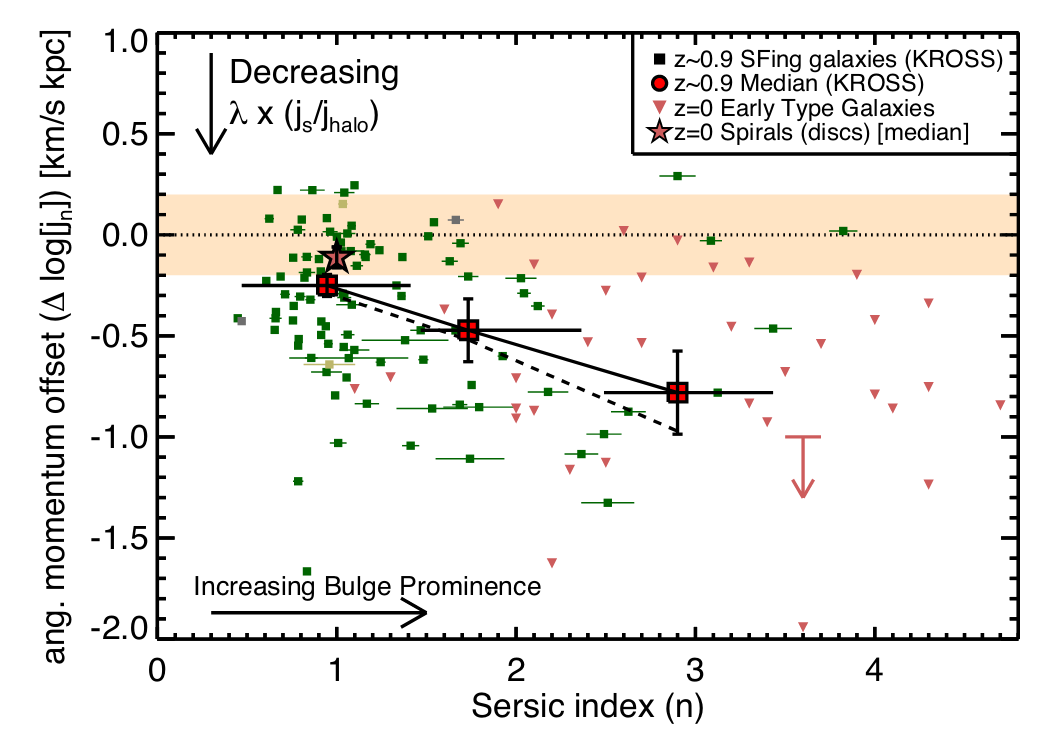
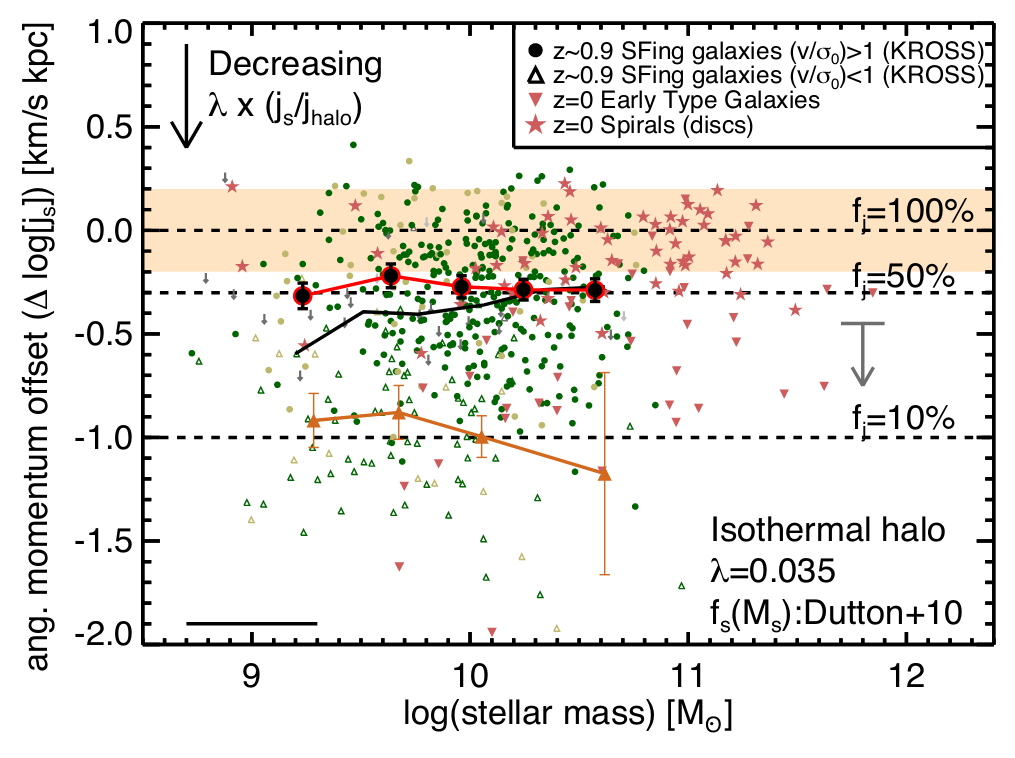
Harrison+17 (KMOS, \(z=1\))






Spiral galaxies \(\leftrightarrow\) high \(J_\star\): also at high-\(z\)
\(M_\star, J_\star,M_\mathrm{BH}\), morpho, bulge fraction, …
What causes what?
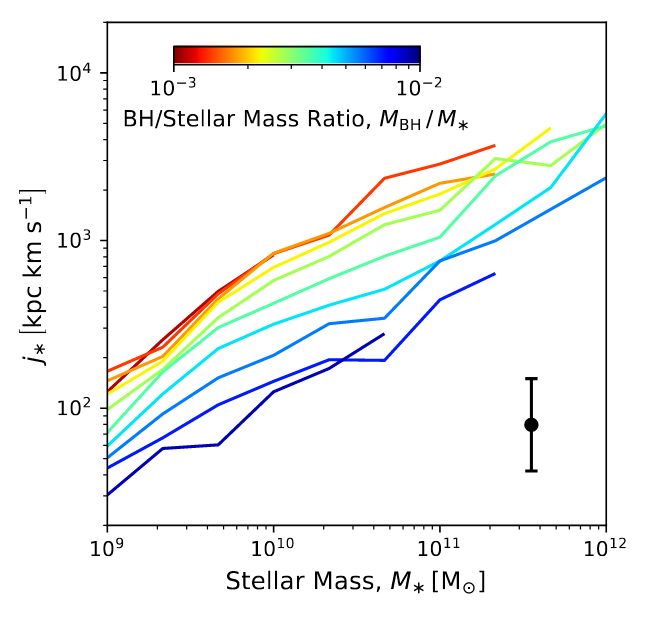
Rodriguez-Gomez+22 (TNG)


Galaxy formation in cosmology: the role of the environment


Environmental effects:
- source of “pollution” in weak lensing surveys
⇒ intrinsic alignment
- extra parameters in semi-analytical models
⇒ galaxy-halo correlation
Mediated by angular momentum?

The origin of angular momentum
Predicting angular momentum



\(z=0\)
\( z = 100\)
Predicting angular momentum



\(z=0\)
\( z = 100\)
\[\mathbf{L}_\mathrm{lin.} \propto \int\mathrm{d}^3q(\mathbf{q}-\bar{\mathbf{q}})\times \nabla\phi\]
Position w.r.t. center
Velocity
[White 84]

\(\mathbf{r}\)\(\times\)\(\mathbf{v}\)
Predicting angular momentum



\(z=0\)
\( z = 100\)
[Porciani+02]

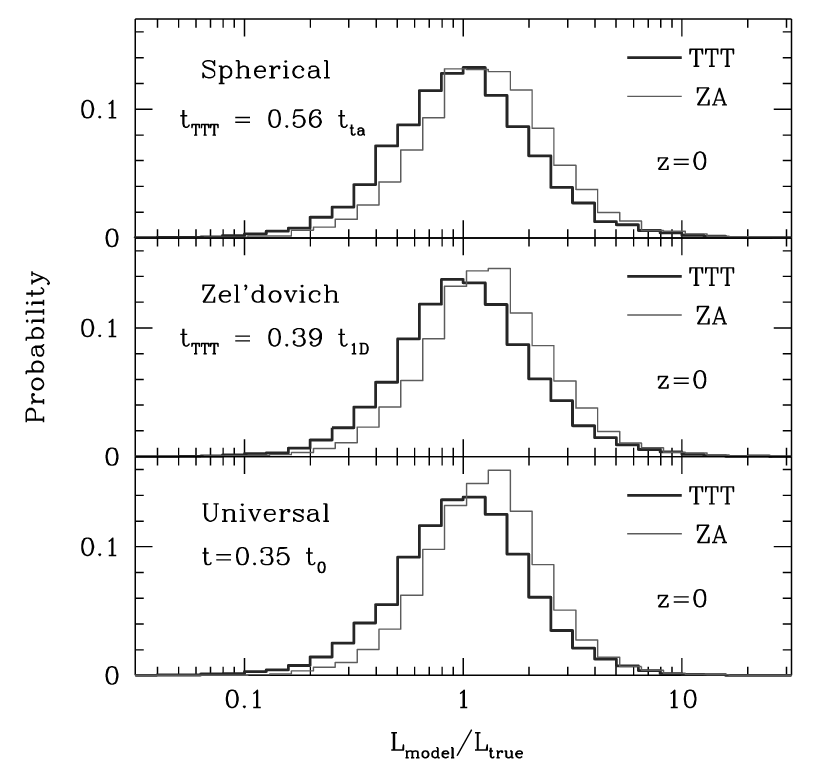
Scatter of 1 dex!
Predicting angular momentum



\(z=0\)
\( z = 100\)
[Genetic modifications: Roth+16, see also Rey&Pontzen 18, Stopyra+20]



Predicting angular momentum




“Tidal torque” prediction
\(N\)-body prediction






Predicting angular momentum




“Tidal torque” prediction
\(N\)-body prediction









Predicting angular momentum



- Angular momentum of individual regions can be predicted accurately.
- AM of halos ⇒ requires boundaries of patch


\[\mathbf{L}_\mathrm{lin.} \propto \int\mathrm{d}^3q(\mathbf{q}-\bar{\mathbf{q}})\times \nabla\phi\]
[On patch boundaries: see Lucie-Smith+18]
Can we control baryonic
angular momentum?
Can we control baryonic
angular momentum?

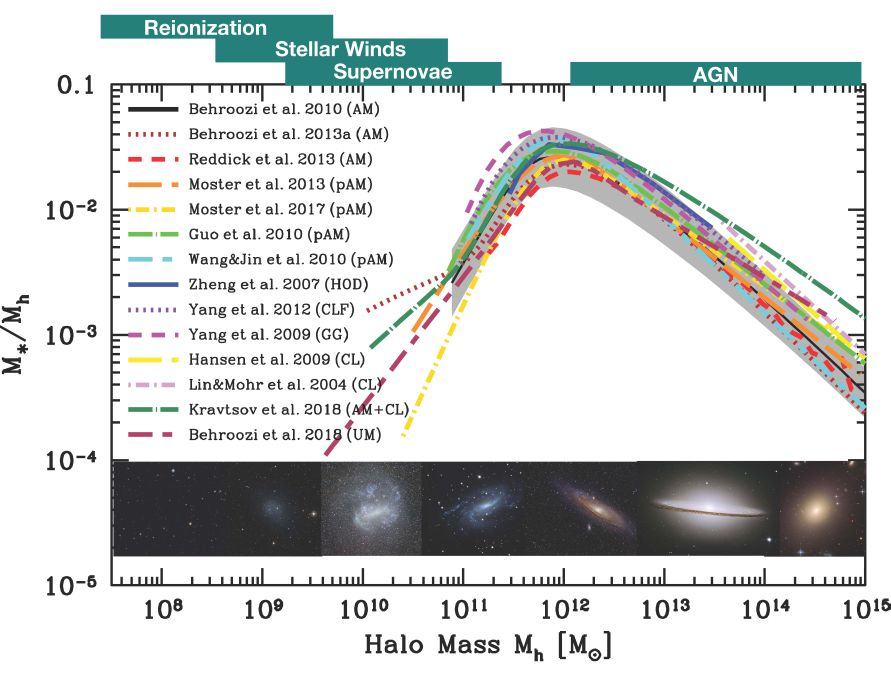
Wechsler & Tinker 18
\({\color{red}M_\star} / M_\mathrm{h} \ll \Omega_b / \Omega_m \)
⇒ baryons & DM stem from different regions


Baryons more strongly bound
⇒ less prone to being ejected


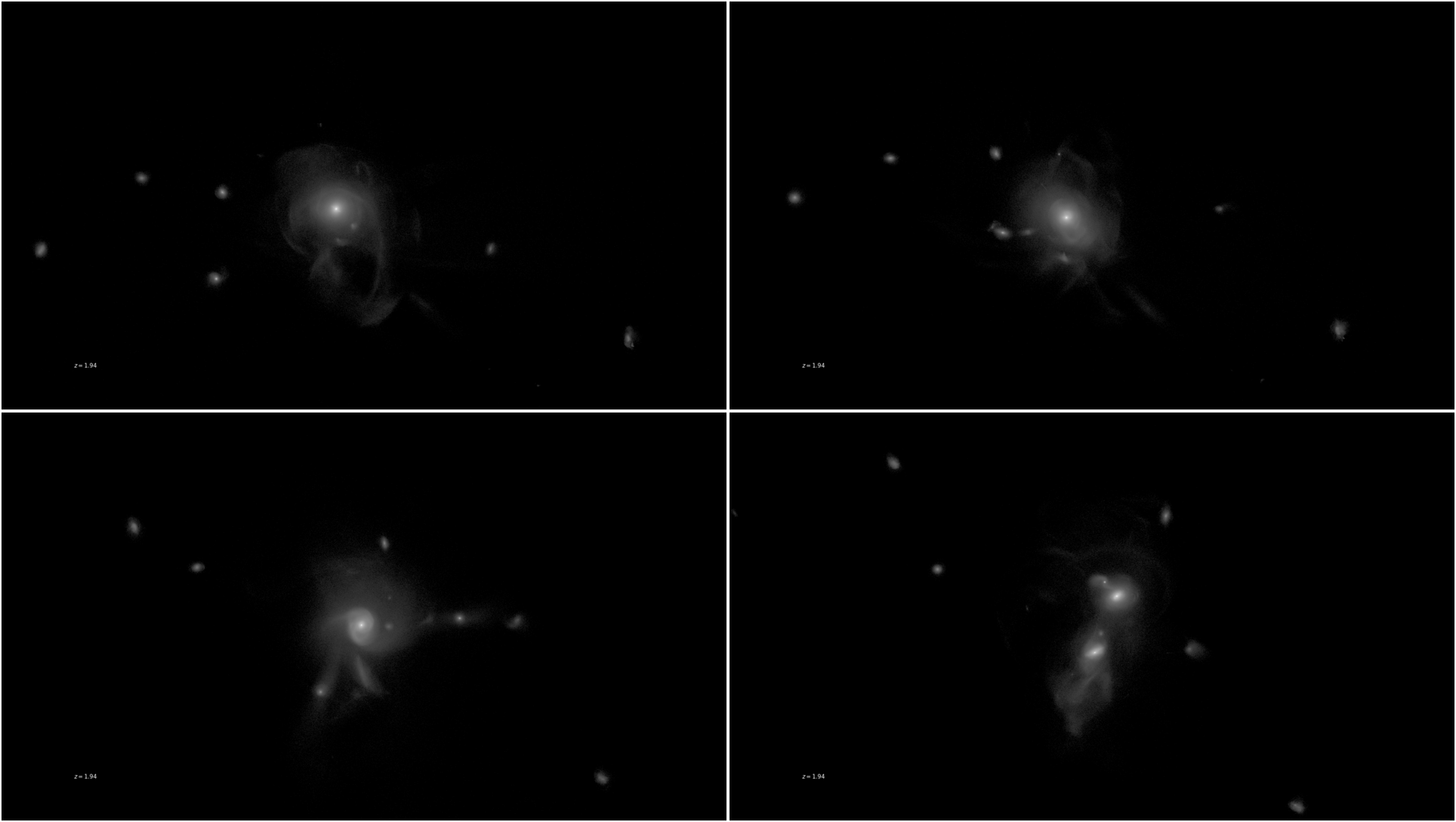
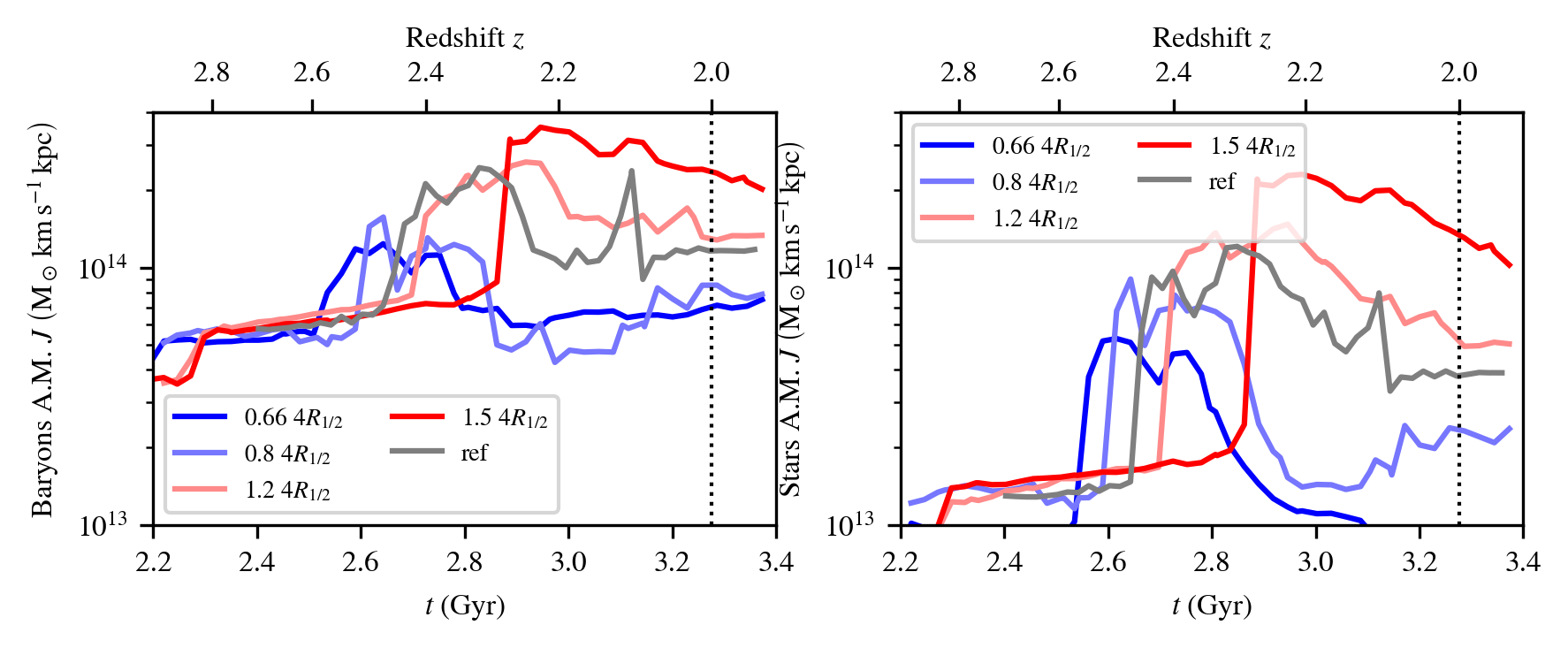
Baryon angular momentum
Simulations (9Mh @ DiRAC):
- Resolve disk height
\(\Delta x = 35\ \mathrm{kpc}\) - \(z \geq 2\), \(M_\mathrm{200c} = 10^{12}\ \mathrm{M}_\odot\)
- SF + AGN & SN feedback
- Modify \(l(z=2)\)
-
Tracer particles
Cadiou+19
\( l_0 \times 0.66\)
\( l_0 \times 0.8\)
\( l_0 \times 1.2\)
\( l_0 \times 1.5\)


\( l_0 \times 1.2\)
\( l_0 \times 1.5\)

\( l_0 \times 0.66\)
\( l_0 \times 0.8\)
\( l_0 \times 0.66\)
\( l_0 \times 0.8\)
\( l_0 \times 1.2\)
\( l_0 \times 1.5\)
Modified at \(z=200\)
Measured at \(z=200\)



- AM of stars originates from initial conditions…
- can be controlled…
- \(j_\star\) regulate galaxy disk, bulge, \(v/\sigma\), \(R_{1/2}\)
- Negligible AGN/SN global self-regulation

\( l_0 \times 1.2\)
\( l_0 \times 1.5\)

\( l_0 \times 0.66\)
\( l_0 \times 0.8\)
Temporary conclusions
-
angular momentum is predictable
-
boundary of halos in the ICs is a hard problem
⇒ limits practicality of predictions (for now)
-
baryons appear to be simpler!
⇒ good news for weak lensing predictions
⇒ key to understand morphology
-
but why do some objects grow their AM faster/slower?


The effect of environment on halo properties
The effect of environment on halo properties
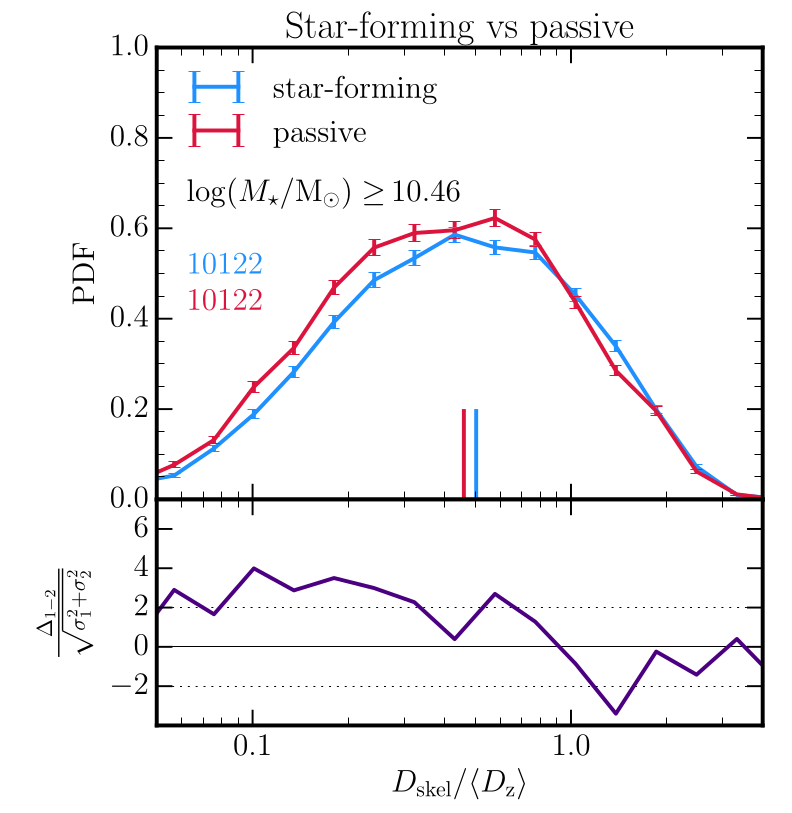
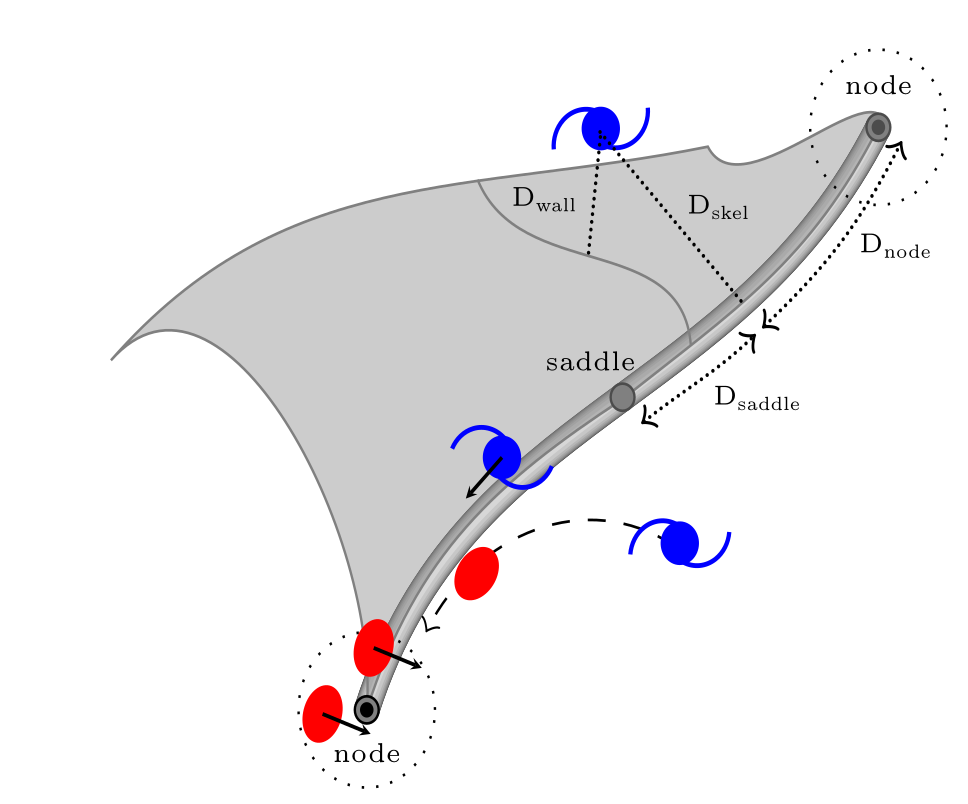
Distance to filament
Kraljic+18 [see also Laigle15, Song+21,…]







What if the galaxy had formed here instead?




What if the galaxy had formed here instead?


or here?
The “splicing” technique


- Generate ICs
- Integrate (\(N\)-nody)
- Select region of interest
- Trace back to ICs
- “Splice”
- Integrate again

\(t\)

Splicing: equivalent of constraining field at all points in spliced region
Splicing in 1D





Splicing in 1D


Most likely* field \(f\) with
- same value in spliced region (\(a\)),
- as close as possible outside (\(b\))



Mathematically \(f\) is solution of:
\( f= a\) in \(\Gamma\)
minimizes \(\mathcal{Q} = (b-f)^\dagger\mathbf{C}^{-1}(b-f) \) outside \(\Gamma\)
The causal origin of DM halo concentration
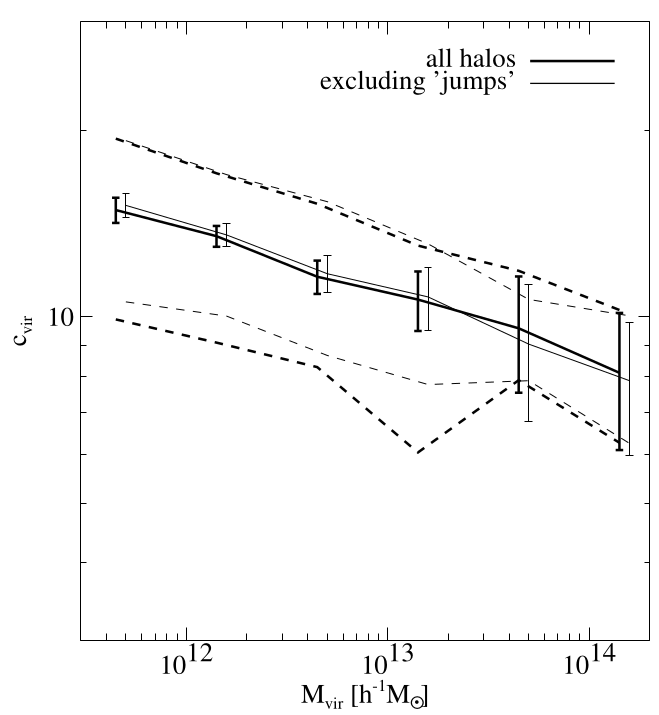

$$\rho_\mathrm{DM}(r) = \frac{\rho_0}{\frac{r}{R_\mathrm{vir}/c} \left(1 + \frac{r}{R_\mathrm{vir}/c}\right)^2}$$
Wechsler+02
Origin of scatter at fixed \(M_\mathrm{vir}\)?
The causal origin of DM halo concentration


\(M^{(1)}_{200\mathrm{c}}, c^{(1)}_\mathrm{NFW}, \dots\)


\(M^{(2)}_{200\mathrm{c}}, c^{(2)}_\mathrm{NFW}, \dots\)


\(M^{(\dots)}_{200\mathrm{c}}, c^{(\dots)}_\mathrm{NFW}, \dots\)


\(M^{(10)}_{200\mathrm{c}}, c^{(10)}_\mathrm{NFW}, \dots\)
Same halo in 10× different environments
Repeat experiment for 7 halos (70 realisations in total)
Same halo in 10× different environments
Repeat experiment for 7 halos (70 realisations in total)


\(M^{(1)}_{200\mathrm{c}}, c^{(1)}_\mathrm{NFW}, \dots\)


\(M^{(2)}_{200\mathrm{c}}, c^{(2)}_\mathrm{NFW}, \dots\)


\(M^{(\dots)}_{200\mathrm{c}}, c^{(\dots)}_\mathrm{NFW}, \dots\)


\(M^{(10)}_{200\mathrm{c}}, c^{(10)}_\mathrm{NFW}, \dots\)

The causal origin of DM halo concentration
Same halo in 10× different environments
Repeat experiment for 7 halos (70 realisations in total)


\(M^{(1)}_{200\mathrm{c}}, c^{(1)}_\mathrm{NFW}, \dots\)


\(M^{(2)}_{200\mathrm{c}}, c^{(2)}_\mathrm{NFW}, \dots\)


\(M^{(\dots)}_{200\mathrm{c}}, c^{(\dots)}_\mathrm{NFW}, \dots\)


\(M^{(10)}_{200\mathrm{c}}, c^{(10)}_\mathrm{NFW}, \dots\)



The causal origin of DM halo concentration
50% of population
Conclusion & outlook
Conclusion & outlook
-
angular momentum is predictable
-
boundary of halos in the ICs is a hard problem
⇒ limits practicality of predictions (for now)
-
baryons can be controlled!
⇒ weak lensing predictions easier than expected?
⇒ role in setting morphology
-
environmental effects can have dramatic impact on halo formation
⇒ 50% of concentration scatter due to env.
⇒ similar impact on galaxy formation?




Conclusion & outlook




Questions?
More infos in Cadiou+21a,b,c (2012.02201, 2107.03407, 2110.05384)
-
angular momentum is predictable
-
boundary of halos in the ICs is a hard problem
⇒ limits practicality of predictions (for now)
-
baryons can be controlled!
⇒ weak lensing predictions easier than expected?
⇒ role in setting morphology
-
environmental effects can have dramatic impact on halo formation
⇒ 50% of concentration scatter due to env.
⇒ similar impact on galaxy formation?

Verify that
\[\xi_\mathrm{lin}(r) \sim \left\langle {\color{green}\underbrace{\delta(x=d)}_\mathrm{in}} {\color{purple} \underbrace{\delta(x=d+r)}_\mathrm{out}}\right\rangle \]
is the same in spliced / ref simulation.

Verify that
\[\xi_\mathrm{lin}(r) \sim \left\langle {\color{green}\underbrace{\delta(x=d)}_\mathrm{in}} {\color{purple} \underbrace{\delta(x=d+r)}_\mathrm{out}}\right\rangle \]
is the same in spliced / ref simulation.

Verify that
\[\xi_\mathrm{lin}(r) \sim \left\langle {\color{green}\underbrace{\delta(x=d)}_\mathrm{in}} {\color{purple} \underbrace{\delta(x=d+r)}_\mathrm{out}}\right\rangle \]
is the same in spliced / ref simulation.


[Danovich+15]
The origin of high \(z\) angular momentum

[Danovich+15]
I. Torque with cosmic web
The origin of high \(z\) angular momentum

[Danovich+15]
I. Torque with cosmic web
II. Transport at constant AM
The origin of high \(z\) angular momentum

[Danovich+15]
I. Torque with cosmic web
II. Transport at constant AM
III. Torque down in inner halo
The origin of high \(z\) angular momentum

[Danovich+15]
I. Torque with cosmic web
II. Transport at constant AM
III. Torque down in inner halo
IV. Mixing in inner disk & bulge
The origin of high \(z\) angular momentum
The origin of high \(z\) angular momentum

[Danovich+15]
IV. Mixing in inner disk & bulge
Fraction that ends up in disk vs. IGM?
Influence of galactic physics?
III. Torque down in inner halo
Origin of torque down (pressure or gravity)?
Loss of link with cosmic AM?
II. Transport at constant AM
Same evolution in cold/hot accretion modes?
I. Torque with cosmic web
Predict pre-accretion AM?
Alignment with environment?
The origin of high \(z\) angular momentum

[Danovich+15]
IV. Mixing in inner disk & bulge
Fraction that ends up in disk vs. IGM?
Influence of galactic physics?
III. Torque down in inner halo
Origin of torque down (pressure or gravity)?
Loss of link with cosmic AM?
See Cadiou+21c
II. Transport at constant AM
Same evolution in cold/hot accretion modes?
I. Torque with cosmic web
Predict pre-accretion AM?
Alignment with environment?
The origin of high \(z\) angular momentum

[Danovich+15]
IV. Mixing in inner disk & bulge
Fraction that ends up in disk vs. IGM?
Influence of galactic physics?
III. Torque down in inner halo
Origin of torque down (pressure or gravity)?
Loss of link with cosmic AM?
II. Transport at constant AM
Same evolution in cold/hot accretion modes?
I. Torque with cosmic web
Predict pre-accretion AM?
Alignment with environment?



+

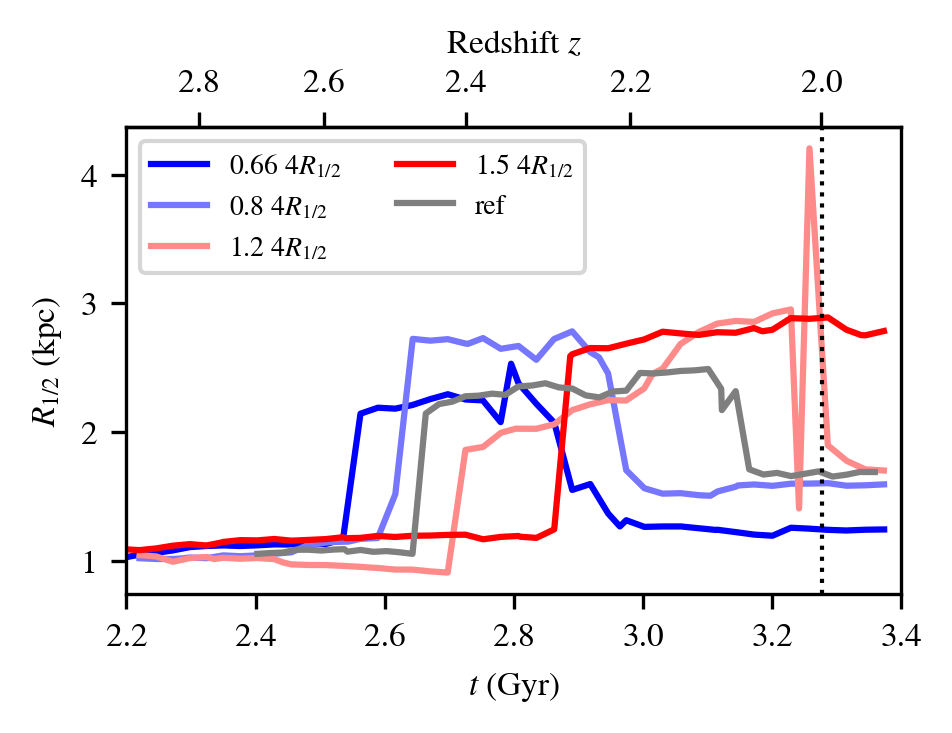
\( R_{1/2} \)
\( l_0 \times 1.2\)
\( l_0 \times 1.5\)

\( l_0 \times 0.66\)
\( l_0 \times 0.8\)

\( l_0 \times 0.66\)
\( l_0 \times 0.8\)
\( l_0 \times 1.2\)
\( l_0 \times 1.5\)


\( l_0 \times 1.2\)
\( l_0 \times 1.5\)

\( l_0 \times 0.66\)
\( l_0 \times 0.8\)



On the causal origin of properties of dark matter halos and galaxies | Lund
By Corentin Cadiou
On the causal origin of properties of dark matter halos and galaxies | Lund
- 429



