背包問題
動態規劃 Dynamic Programming
林芊妘
背包問題是組合優化問題中一個經典的範例,目的是: 在容量有限的背包裡,選擇價值最大化的物品組合

背包是一種比喻
在日常生活中我們常常面臨這樣的選擇
- 書包容量有限,段考前要帶什麼回家抱佛腳
- 錢包預算有限,要買什麼最能填飽肚子
- 考前自習時間有限,要讀什麼才能保住學分

容量W
⚾
重量W1
價值V1
🥘
重量W2
價值V2
👔
重量W3
價值V3
目標:總重量<=w;總價值最大

0-1背包問題
容量W
⚾
重量W1
價值V1
🥘
重量W2
價值V2
👔
重量W3
價值V3
物品只能取一次或不取
重量:1
價值:3
重量:4
價值:4
重量:3
價值:7
容量:5

| 0 | 1 | 2 | 3 | 4 | 5 | |
|---|---|---|---|---|---|---|
| 0 | ||||||
| ⚾(1,3) | ||||||
| 🥘(4,4) | ||||||
| 👔(3,7) |






| 0 | 1 | 2 | 3 | 4 | 5 | |
|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| ⚾(1,3) | ||||||
| 🥘(4,4) | ||||||
| 👔(3,7) |
任意背包容量中,不放入任何物品,則最大價值皆為0






| 0 | 1 | 2 | 3 | 4 | 5 | |
|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| ⚾(1,3) | 0 | |||||
| 🥘(4,4) | 0 | |||||
| 👔(3,7) | 0 |
背包容量為0,因此無法裝入任何物品,則最大價值皆為0






| 0 | 1 | 2 | 3 | 4 | 5 | |
|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| ⚾(1,3) | 0 | 3 | ||||
| 🥘(4,4) | 0 | |||||
| 👔(3,7) | 0 |










| 0 | 1 | 2 | 3 | 4 | 5 | |
|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| ⚾(1,3) | 0 | 3 | 3 | 3 | 3 | 3 |
| 🥘(4,4) | 0 | |||||
| 👔(3,7) | 0 |
*先以行確認






| 0 | 1 | 2 | 3 | 4 | 5 | |
|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| ⚾(1,3) | 0 | 3 | 3 | 3 | 3 | 3 |
| 🥘(4,4) | 0 | 3 | ||||
| 👔(3,7) | 0 |






| 0 | 1 | 2 | 3 | 4 | 5 | |
|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| ⚾(1,3) | 0 | 3 | 3 | 3 | 3 | 3 |
| 🥘(4,4) | 0 | 3 | 3 | 3 | ||
| 👔(3,7) | 0 |






| 0 | 1 | 2 | 3 | 4 | 5 | |
|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| ⚾(1,3) | 0 | 3 | 3 | 3 | 3 | 3 |
| 🥘(4,4) | 0 | 3 | 3 | 3 | 4 | |
| 👔(3,7) | 0 |






| 0 | 1 | 2 | 3 | 4 | 5 | |
|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| ⚾(1,3) | 0 | 3 | 3 | 3 | 3 | 3 |
| 🥘(4,4) | 0 | 3 | 3 | 3 | 4 | 7 |
| 👔(3,7) | 0 |






| 0 | 1 | 2 | 3 | 4 | 5 | |
|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| ⚾(1,3) | 0 | 3 | 3 | 3 | 3 | 3 |
| 🥘(4,4) | 0 | 3 | 3 | 3 | 4 | 7 |
| 👔(3,7) | 0 | 3 |






| 0 | 1 | 2 | 3 | 4 | 5 | |
|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| ⚾(1,3) | 0 | 3 | 3 | 3 | 3 | 3 |
| 🥘(4,4) | 0 | 3 | 3 | 3 | 4 | 7 |
| 👔(3,7) | 0 | 3 | 3 |






| 0 | 1 | 2 | 3 | 4 | 5 | |
|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| ⚾(1,3) | 0 | 3 | 3 | 3 | 3 | 3 |
| 🥘(4,4) | 0 | 3 | 3 | 3 | 4 | 7 |
| 👔(3,7) | 0 | 3 | 3 | 7 |






| 0 | 1 | 2 | 3 | 4 | 5 | |
|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| ⚾(1,3) | 0 | 3 | 3 | 3 | 3 | 3 |
| 🥘(4,4) | 0 | 3 | 3 | 3 | 4 | 7 |
| 👔(3,7) | 0 | 3 | 3 | 7 | 10 |






| 0 | 1 | 2 | 3 | 4 | 5 | |
|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| ⚾(1,3) | 0 | 3 | 3 | 3 | 3 | 3 |
| 🥘(4,4) | 0 | 3 | 3 | 3 | 4 | 7 |
| 👔(3,7) | 0 | 3 | 3 | 7 | 10 | 10 |
每格中的值即為當下情況的最優解,因此右下角的值即為答案






以程式的角度思考
| 0 | 1 | 2 | 3 | 4 | 5 | |
|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| ⚾(1,3) | 0 | 3 | 3 | 3 | 3 | 3 |
| 🥘(4,4) | 0 | 3 | 3 | 3 | 4 | 7 |
| 👔(3,7) | 0 | 3 | 3 | 7 | 10 | 10 |
不納入棒球的最優解
0






以程式的角度思考
| 0 | 1 | 2 | 3 | 4 | 5 | |
|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| ⚾(1,3) | 0 | 3 | 3 | 3 | 3 | 3 |
| 🥘(4,4) | 0 | 3 | 3 | 3 | 4 | 7 |
| 👔(3,7) | 0 | 3 | 3 | 7 | 10 | 10 |
0
0+3
背包容量減去棒球重量時的最優解






| 0 | 1 | 2 | 3 | 4 | 5 | |
|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| ⚾(1,3) | 0 | 3 | 3 | 3 | 3 | 3 |
| 🥘(4,4) | 0 | 3 | 3 | 3 | 4 | 7 |
| 👔(3,7) | 0 | 3 | 3 | 7 | 10 | 10 |
以程式的角度思考
不納入火鍋料的最優解
3






| 0 | 1 | 2 | 3 | 4 | 5 | |
|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| ⚾(1,3) | 0 | 3 | 3 | 3 | 3 | 3 |
| 🥘(4,4) | 0 | 3 | 3 | 3 | 4 | 7 |
| 👔(3,7) | 0 | 3 | 3 | 7 | 10 | 10 |
以程式的角度思考
3
背包容量減去火鍋料重量時的最優解
3+4






| 0 | 1 | 2 | 3 | 4 | 5 | |
|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| ⚾(1,3) | 0 | 3 | 3 | 3 | 3 | 3 |
| 🥘(4,4) | 0 | 3 | 3 | 3 | 4 | 7 |
| 👔(3,7) | 0 | 3 | 3 | 7 | 10 | 10 |
以程式的角度思考
4
不納入襯衫的最優解






| 0 | 1 | 2 | 3 | 4 | 5 | |
|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| ⚾(1,3) | 0 | 3 | 3 | 3 | 3 | 3 |
| 🥘(4,4) | 0 | 3 | 3 | 3 | 4 | 7 |
| 👔(3,7) | 0 | 3 | 3 | 7 | 10 | 10 |
以程式的角度思考
4
背包容量減去襯衫重量時的最優解
3+7






#include <bits/stdc++.h>
using namespace std;
int main(){
//m為物品數,n為背包容量
int m,n;
while(cin>>m>>n){
//各物品重量與價值
int w[m],v[m];
//dp為表格
int dp[m+1][n+1];
for(int i=0;i<m;i++)
cin>>w[i]>>v[i];
memset(dp,0,sizeof(dp));//初始化把表格清空
//dp[i][j]為表格中最優解
for(int i=0;i<m;i++){
for(int j=0;j<=n;j++){
//物品重量小於背包容量
if(w[i]<=j){
dp[i+1][j]=max(dp[i][j],
dp[i][j-w[i]]+v[i]);
}
//容量不足繼承上方的
else dp[i+1][j]=dp[i][j];
}
}
cout<<dp[m][n]<<endl;
}
}二維版本
二維–>一維
| 二維 | 一維 | |
|---|---|---|
| 可讀性 | 容易 | 抽象 |
| 程式長度 | 較長 | 精簡 |
| 儲存空間 | 大 | 小 |
| 更新順序 | 皆可 | 倒序 |
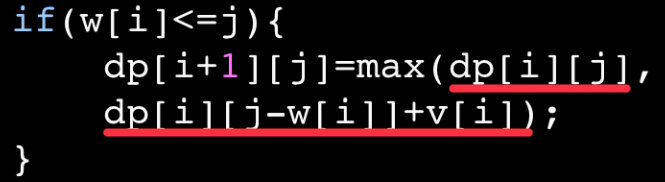
考慮同一層i

dp[5] = max(dp[5], dp[5-w1] + v1)
dp[4] = dp[4-w1] + v1
dp[3] = dp[3-w1] + v1
dp[2] = dp[2-w1] + v1
dp[1] = dp[1-w1] + v1可改成一維!
物品1
物品2
dp[5] = max(dp[5], dp[5-w2] + v2)
...
dp[w2] = max(dp[w2], dp[0] + v2)#include<bits/stdc++.h>
using namespace std;
int main(){
int m,n;
while(cin>>m>>n){
int w[m],v[m];
for(int i=0;i<m;i++){
cin>>w[i]>>v[i];
}
int dp[n+1]={0};
//遍歷每一個物品
for(int i=0;i<m;i++){
//這裡從n到w[i]倒序遍歷
for(int j=n;j>=w[i];j--){
//dp[j]表示容量為j時的最優解
dp[j]=max(dp[j],dp[j-w[i]]+v[i]);
}
}
cout<<dp[n]<<endl;//最終背包容量為n時的最大價值
}
}一維版本
你是個無課玩家,每天只有10點體力值,以下有5隻哥布林供你攻略,由於你前幾天抽中精靈,所以每次攻略都能成功,你想在今天獲得最多經驗值該攻略哪幾隻哥布林呢?
練習題-哥布林攻略(畫表格)
| 消耗體力 | 經驗值 | |
|---|---|---|
| 勤儉持家哥布林 | 2 | 6 |
| 肥宅哥布林 | 3 | 2 |
| 180哥布林 | 4 | 5 |
| 狗狗哥布林 | 4 | 7 |
| 嬰兒哥布林 | 6 | 4 |
下週上課交來給我可以領餅乾!!
完全背包問題
容量W
⚾
重量W1
價值V1
🥘
重量W2
價值V2
👔
重量W3
價值V3
物品可以無限取
重量:1
價值:3
重量:4
價值:4
重量:3
價值:7
容量:5

#include <bits/stdc++.h>
using namespace std;
int main(){
//m為物品數,n為背包容量
int m, n;
cin>>m>>n;
//物品的重量與價值
int w[m], v[m];
for (int i=0;i<m;i++){
cin >> w[i] >> v[i];
}
int dp[n+1]={0};
//每個物品都試著放進背包
for (int i=0;i<m;i++) {
// 正序:因為可以重複放
for (int j=w[i];j<=n;j++) {
//dp[j]表示容量為j時的最優解
dp[j]=max(dp[j],dp[j-w[i]]+v[i]);
}
}
//輸出最優解
cout<<dp[n]<<endl;
return 0;
}
背包問題
By chainy
背包問題
- 144



