preon: digital signature from zk-SNARK
The preon team
Team
- Hon Hai Research Institute
- Yu-Shian Chen & Wei-Bin Lee
- BTQ
- Shiuan Fu, Wei-Chih Hong, Jen-Hsuan Hsiang, Sheng-Te Hu, & Po-Chun Kuo
- Academia Sinica
- Ming-Shing Chen & Bo-Yin Yang (TBC)
- Feng-Hao Liu, Washington State University
- Justin Thaler, Georgetown University
- Eylon Yogev, Bar-Ilan University
- Chen-Mou Cheng, Chang Gung University
Outline
- NIST PQC
- preon
- zk-SNARK: an anatomy
- Commitment
- I(O)P & ZKP
- Schnorr's ZKP for DLP
- Aurora
- Feb 2016: Announced in PQCRYPTO
- Need to run on classical, non-quantum computers
- Wide spectrum: From extremely constrained devices to limited communication bandwidth
- July 2022: To standardize 4 algorithms
- July 2023: To consider 40 additional signature schemes
| CRYSTALS-Kyber | Lattice (MLWE) | KEM |
| CRYSTALS-Dilithium | Lattice (MLWE) | Signature |
| Falcon | Lattice (NSIS) | Signature |
| SPHINCS+ | Hash-based | Signature |


preon:
beyond digital signature
- Standard digital signature on message \( x \):
- "I swear that the signer said \( x \)."
- Beyond digital signature:
- "The signer said \( \color{red}x\color{black} \), which I'm not going to disclose here, but I swear that \( f(\color{red}x\color{black})=y \)."
Example
- CA signs Cert: "Batman was born on Jan 1, 1976"
- \( f(x,\color{red}w\color{black})=1 \) if and only if:
- \( \color{red}w\color{black} \) is a valid certificate signed by CA
- \( \color{red}w\color{black} \) says as of today, \( x \) is over 18 years old
- Beers for Batman if \( f(\text{Batman},\color{red}\text{Cert}\color{black})=1 \)
preon: under the hood
- preon \( \approx \) Aurora + AES
- Aurora: post-quantum zk-SNARK (to be detailed)
- AES as one-way function
- Public key is the ciphertext of encrypting a random plaintext using private key
- Optimization: replace prime field with binary field
- 14240 \( \rightarrow \) 3440 constraints
- 4x speedup, with additional 2\( \text{--} \)3x via AFFT
- About 20% smaller signature
preon+: performance
| Security | Private key | Public key | Signature | Key gen | Sign | Verify |
|---|---|---|---|---|---|---|
| 128-bit (A1) | 16 | 32 | 44.7K | 2us | 490ms | 7.2ms |
| 128-bit (A2) | 16 | 32 | 49.7K | 2us | 326ms | 8.5ms |
| 128-bit (B) | 16 | 32 | 90.1K | 2us | 343ms | 16.8ms |
| 192-bit (A) | 24 | 56 | 101.6K | 2us | 497ms | 47ms |
| 192-bit (B) | 24 | 56 | 201.6K | 2us | 623ms | 103ms |
| 256-bit (A) | 32 | 64 | 186.1K | 2us | 1399ms | 149ms |
| 256-bit (B) | 32 | 64 | 369K | 2us | 1773ms | 330ms |
Where we are & to go
- preon accepted by NIST as complete & proper
- Preliminary security analysis shows even Aggressive (A) meets NIST's requirement, with Balanced (B) as backup
- preon+ incorporates Cantor basis & more efficient encoding/padding
- Future works
- More security analysis
- Further optimized implementations
- Must have: CPU, GPU, FPGA
- Nice to have: ASIC
Anatomy of zk-SNARK
Serialization via commitment
(How to play rock-paper-scissors over internet)
- Cryptographic commitment
- Commit: \( c=\text{commit}(r,m) \)
- Verify: \( \text{verify}\Big(r,m,c\Big)? \)
- Security properties
- Hiding: difficult to find \( m \) given \( c=\text{commit}\left(r,m\right) \)
- Binding: difficult to find \( r',m'\neq m \) s.t. \( \text{verify}\Big(r',m',\text{commit}(r,m)\Big) \)
Proving \( x\in X \) via Merkle tree
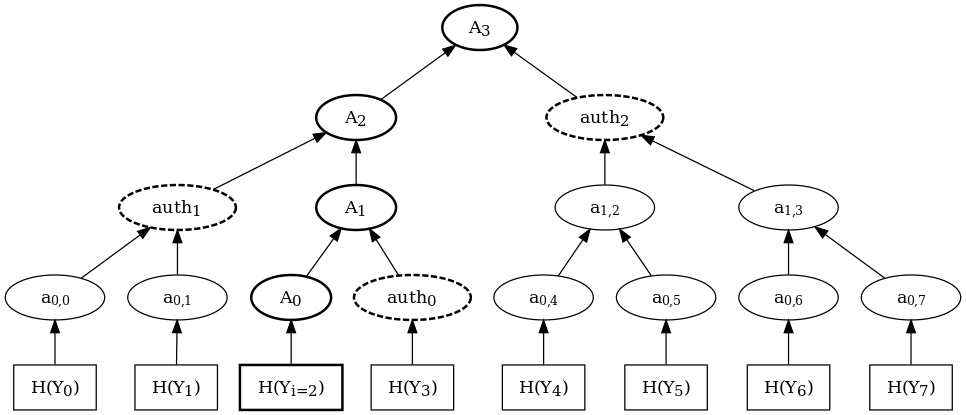
Proving \( f(x)=y \)
- Syntax of (polynomial) functional commitment
- \( c=\text{commit}(r,f) \)
- \( (y,\pi)=\text{eval}(r,f,x) \)
- \( \text{verify}\Big(c,x,y,\pi\Big) \) iff \( \exists r\text{ s.t. }c=\text{commit}(r,f) \) and \( f(x)=y \)
- Example (Merkle tree)
- Leaves \( y_0,y_1,\ldots,y_{n-1} \) define \( f:\Big\{0,1,\ldots,n-1\Big\}\rightarrow Y \)
- Authentication path encodes (binary expansion of) \( i\in\Big\{0,1,\ldots,n-1\Big\} \) and thus proves \( f(i)=y_i \)
Why polynomials?
- \( f_{v+w}=f_v+f_w, f_{v\odot w}=f_vf_w \) for coordinate-wise product \( \odot \) \[ \Big(\because\text{ev}\in k[X]\times k\rightarrow k\cong k[X]\rightarrow k\rightarrow k\Big) \]
- Lemma [Schwartz-Zippel] \[ \text{Pr}_{r\in k}\Big(f(r)=g(r)\Big)\leq\frac{d}{|k|}\text{ for }f\neq g\text{ with }\deg f,\deg g\leq d \]
- Zero test: \( f(\omega)=0\ \forall\omega\in\Omega \)
- Sum check: \( \sum_{\omega\in\Omega}f(\omega)=0 \)
- Product check: \( \prod_{\omega\in\Omega}f(\omega)=1 \)
Interactive (oracle) proof
- IP allows Prover P to prove Statement S to (computationally bounded) Verifier V via dialogue
- Completeness: If S is true, then V should be convinced with probability 1
- Soundness: If S is false, then V should be convinced with a (very) small probability
- Example (trivial): NP \( \subset \) IP
- IOP: dialogue consists of probabilistically checkable proofs, implemented by e.g. functional commitment
Zero-knowledge IP
- V learns nothing beyond S is true
- Consider special S: \( y=f(x,\color{red}w\color{black}) \)
- Can simulate the dialogues without knowing \(\color{red}w\color{black}\)
- Example: Blind V with two colored balls
Toy example
- Prover: "I know integers \( \color{red}p\color{black},\color{red}q\color{black} \) s.t. \( n=\color{red}pq\color{black} \)"
- Prover commits to three polynomial functions: \[ \color{red}r_p\color{black}X+\color{red}p\color{black},\color{red}r_q\color{black}X+\color{red}q\color{black},\text{ and }\color{red}r_pr_q\color{black}X^2+(\color{red}r_pq\color{black}+\color{red}pr_q\color{black})X+n \]
- Verifier challenges Prover with random \( r \) and checks whether \( (\color{red}r_p\color{black}r+\color{red}p\color{black})(\color{red}r_q\color{black}r+\color{red}q\color{black})\stackrel{?}{=}\color{red}r_pr_q\color{black}r^2+(\color{red}r_pq\color{black}+\color{red}pr_q\color{black})r+n \)
- Lemma [Schwartz-Zippel] \[ \text{Pr}_{r\in k}\Big(f(r)=g(r)\Big)\leq\frac{d}{|k|}\text{ for }f\neq g\text{ with }\deg f,\deg g\leq d \]
Schnorr's ZKP for DLP
- S: "I know \( \color{red}x\color{black} \) s.t. \( y=g^{\color{red}x\color{black}} \)"
- P \( \rightarrow \) V: \( r=g^{\color{red}k\color{black}} \)
- P \( \leftarrow \) V: \( e \)
- P \( \rightarrow \) V: \( s=\color{red}k\color{black}-\color{red}x\color{black}e \)
- V checks: \( r\stackrel{?}{=}g^sy^e\left(=g^{\color{red}k\color{black}-\color{red}x\color{black}e}(g^x)^e\right) \)
- Fiat-Shamir heuristic turns (most) IP to NIROP (Non-Interactive Random-Oracle Proof)
- Schnorr's signature: \( \pi=(r,s) \) for \( e=H(r||m) \)
- zk-NARK (Noninteractive ARgument of Knowledge)
Knowledge extractor
How Sony PS3 got hacked in 2011: \[ \left\{\begin{aligned} s_1 & =\color{red}k\color{black}-\color{red}x\color{black}e_1 \\ s_2 &= \color{red}k\color{black}-\color{red}x\color{black}e_2 \end{aligned}\right. \]
zk-SNARK
- Consider special zk-NARK:
- Proof \( \pi \) proves P knows a \( \color{red}w\color{black} \) s.t. \( y=f(x,\color{red}w\color{black}) \)
- If \( \pi \) is "small" compared with \( f \), e.g., \( |\pi|=O(\log|f|) \), then we say it is succinct, or zk-SNARK
- Questions
- What can we do with a zk-SNARK?
- How to "compress" \( \pi \)?
- How to encode (interesting) \( f \)?
zk-SNARKing C2PA
-
Coalition for Content Provenance and Authenticity
- Camera signs all photos taken: \( s=\text{sign}(p) \)
- Publisher/consumer verifies: \( \text{verify}(p,s)? \)
- What if \( p'=f(p) \) where \( f \) crops, resizes, rotates, ... \( p \)?
- \( \pi \): "I know \( \color{red}p\color{black},\color{red}s\color{black} \) s.t. \( \text{verify}(\color{red}p\color{black},\color{red}s\color{black}) \) & \( p'=f(\color{red}p\color{black}) \)"
- For zk-SNARKs, \( |\pi|\ll |f|=\mathcal O(|p|) \)
EF's semaphore
- "Users who broadcast a signal will not expose their identity"
- "Specifically, an adversary will only know they're a user in the group, but not which user"
- "Users cannot broadcast two different signals on the same topic twice"
How to implement?
- Identity commitment integrity: \[ \text{id}_\text{comm}=\text{Commit}_{\text{id}_\text{trapdoor}}(\text{id}_\text{pub},\text{id}_\text{nullifier}) \]
- Merkle path validity: \[ (\text{id\textunderscore path},\text{id\textunderscore path\textunderscore index})\text{ is a valid Merkle path from id}_\text{comm}\text{ to root} \]
- Nullifiers hash integrity: \[ \text{nullifiers\textunderscore hash}=\text{PRF}_{\text{id}_\text{nullifier}}(\text{external\textunderscore nullifier},\text{id\textunderscore path\textunderscore index}) \]
- Signal authorization: \[ \text{Verify}(\text{id}_\text{pub},(\text{external\textunderscore nullifier},\text{signal\textunderscore hash}),\text{signature}) \]
Recipe: RS-encoded IOP
- Think of \( v\in V \) as a function \( H\rightarrow F_q \) for \( |H|=\dim V \)
- Encode \( v \) as \( f_v \) via Lagrange interpolation
- \( f_v(X)=r(X)+q(X)\prod_{h\in H}(X-h) \)
- S.t. \( \forall h\in H,r(h)=v(h) \)
- V can now query \( f_v(x) \) for some \( x\in L \)
- Intuition: ZK if \( H\cap L=\varnothing \) and \( \deg q \) is large enough
- (FRI) low-degree test: Check if \( \deg f_v \) is small enough
- Encode \( y=f(x,\color{red}w\color{black}) \) into R1CS: \( Az\odot Bz=Cz \), where:
- \( A,B,C \) are matrices depending on \( f \)
- \( z=\begin{bmatrix} 1 & u & \color{red}w\color{black} & x & y \end{bmatrix}^T \)
- \( u \) is auxiliary variables
- Lincheck RS-encoded IOP: \( y_A=Az, y_B=Bz, y_C=Cz \)
- Rowcheck RS-encoded IOP: \( y_A\odot y_B=y_C \)
Expressiveness of R1CS
\[ y=x^3: \boxed{\begin{aligned} x\cdot x & =u \\ u\cdot x & =y \end{aligned}} \]
\[ 0\leq x<8: \boxed{\begin{aligned} 1\cdot(x_0+2x_1+4x_2) & =x \\ x_0\cdot x_0 & =x_0 \\ x_1\cdot x_1 & =x_1 \\ x_2\cdot x_2 & =x_2 \end{aligned}} \]
\(r=\) if \(b\) then \(t\) else \(f\): \[ \boxed{\begin{aligned} (t-f)\cdot b & =r-f \\ b\cdot b & =b \end{aligned}} \]
Got DSL?
Revisiting Merkle tree

In ZoKrates
- Witness contains array of arrays of hash values along authentication path
- Well-known trick to include the indices of these hash values at each level
- Not strictly necessarily but for easy programming
- Will expand to nested if-then-else in R1CS anyway
field mut digest = leaf;
for u32 i in 0..DEPTH {
assert(path[i][indices[i]] == digest);
digest = hash(path[i]);
}
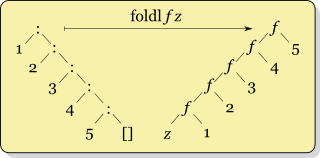
assert(digest == root);\(\text{\tt fold}\) to rescue in Keelung
\(\text{\tt foldl :: Foldable t => (b -> a -> b) -> b -> t a -> b}\)
merkleProof :: Int -> Number -> Comp ()
merkleProof depth root = do
leaf <- inputNum
path <- inputs2 depth 2
digest <- foldlM (\digest p -> do
assert (digest `existsIn` p)
hash p)
leaf
path
assert (digest `Eq` root)Thank you!
Questions or comments?
preon
By Chen-Mou Cheng
preon
- 1,199



