Dynamic Programming Series
Dynamic Programming Series
Day 5 :
Unique Binary Search Trees..!!
Problem Description
Given an integer N, find and return the count of unique Binary search trees (BSTs) possible with nodes valued from 1 to N.
Problem Description
Given an integer N, find and return the count of unique Binary search trees (BSTs) are possible with nodes valued from 1 to N.
What is Binary search tree?
What is Binary search tree?
A Binary search tree is a tree with the following properties :
What is Binary search tree?
A Binary search tree is a tree with the following properties :
- The left subtree of a node contains only nodes with values less than the node's value.
What is Binary search tree?
A Binary search tree is a tree with the following properties :
- The left subtree of a node contains only nodes with values less than the node's value.
2. The right subtree of a node contains only nodes with values greater than the node's value.
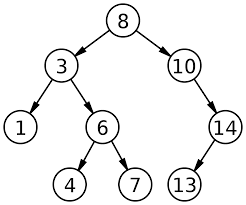
Binary search tree example!!!
Binary search tree example!!!
Examples of the problem
Example 1 :
Let us take n = 2.
Examples of the problem
Example 1 :
Let us take n = 2.
1
2
Examples of the problem
Example 1 :
Let us take n = 2.
1
2
1
2
Examples of the problem
Example 1 :
Let us take n = 2.
1
2
1
2
Two BST's are possible..!!
Examples of the problem
Example 2 :
Let us take n = 3.
Examples of the problem
Example 2 :
Let us take n = 3.
1
3
2
Examples of the problem
Example 2 :
Let us take n = 3.
1
3
2
3
2
1
Examples of the problem
Example 2 :
Let us take n = 3.
1
3
2
1
3
2
1
3
2
Examples of the problem
Example 2 :
Let us take n = 3.
1
3
1
2
2
1
3
2
1
3
2
3
Examples of the problem
Example 2 :
Let us take n = 3.
1
3
1
2
2
1
3
2
1
3
2
3
1
2
3
Examples of the problem
Example 2 :
Let us take n = 3.
1
3
1
2
2
1
3
2
1
3
2
3
1
2
3
5 unique BST's are possible..!!
Now coming back to the problem..!!
Now coming back to the problem..!!
Let's forget dp for some time and see what observations we can make of the Binary search tree.
Now coming back to the problem..!!
Let's forget dp for some time and see what observations we can make of the Binary search tree.
If we have nodes from 1 to n in a binary search tree and root node is some t.
Now coming back to the problem..!!
Let's forget dp for some time and see what observations we can make of the Binary search tree.
If we have nodes from 1 to n in a binary search tree and root node is some t.
Then there will be nodes from 1 to t-1 in left subtree and t+1 to n in right subtree.
4
2
6
1
3
5
7
4
2
6
1
3
5
7
Nodes from
1-3
4
2
6
1
3
5
7
Nodes from
1-3
That means left subtree contains nodes 1 to t-1.
4
2
6
1
3
5
7
Nodes from
1-3
That means left subtree contains nodes 1 to t-1.
Total nodes in left subtree = t-1
4
2
6
1
3
5
7
Nodes from
5 to 7
4
2
6
1
3
5
7
Nodes from
5 to 7
Number of nodes in right subtree is :
4
2
6
1
3
5
7
Nodes from
5 to 7
Number of nodes in right subtree is :
Total nodes - (nodes in left subtree + root node)
4
2
6
1
3
5
7
Nodes from
5 to 7
Number of nodes in right subtree is :
Total nodes - (nodes in left subtree + root node)
7 - (3+1) = 3 nodes
OBSERVATIONS THAT WE MADE:
1. Left subtree consist of t-1 nodes.
OBSERVATIONS THAT WE MADE:
1. Left subtree consist of t-1 nodes.
2. Right subtree consist of total nodes - (nodes in left subtree + root node)
= n - (t-1+1)
= (n - t) nodes
Now we can develop a recursive solution!!!
Suppose we want to calculate how many possible BST's exist for a particular root node 'i' with total nodes n.
Now we can develop a recursive solution!!!
Suppose we want to calculate how many possible BST's exist for a particular root node 'i' with total nodes n.
UniqueBst(i)
UniqueBst(i-1)
UniqueBst(n-i)
What will be the base case?
What will be the base case?
1. UniqueBst(0) = 1
2. UniqueBst(1) = 1
So, now we have seen recursive solution..!!
What will be the base case?
1. UniqueBst(0) = 1
2. UniqueBst(1) = 1
So, now we have seen recursive solution..!!
But, is the solution optimal ?
The answer is NO
The answer is NO
Because we have exponential time complexity..!!
The answer is NO
Because we have exponential time complexity..!!
1,2,3.........n
......
Ubst(i-1)+ubst(n-i)
Ubst(i-1)+ubst(n-i)
Ubst(i-1)+ubst(n-i)
Ubst(i-1)+ubst(n-i)
The answer is NO
Because we have exponential time complexity..!!
1,2,3.........n
......
Ubst(i-1)+ubst(n-i)
Ubst(i-1)+ubst(n-i)
Ubst(i-1)+ubst(n-i)
Ubst(i-1)+ubst(n-i)
Overall time complexity :
The answer is NO
Because we have exponential time complexity..!!
1,2,3.........n
......
Ubst(i-1)+ubst(n-i)
Ubst(i-1)+ubst(n-i)
Ubst(i-1)+ubst(n-i)
Ubst(i-1)+ubst(n-i)
Overall time complexity :
WORST TIME COMPLEXITY!!
But the best part is we have too much of repetitions!!
But the best part is we have too much of repetitions!!
i.e., Overlapping subproblems
But the best part is we have too much of repetitions!!
i.e., Overlapping subproblems
So, lets analyze, how we can make a DP approach..!!
main()
{
int n;
cin >> n;
int*dp = new int[n+1]();
dp[0] = 1;
dp[1] = 1;
for(int i = 2; i<=n; i++)
{
for(int j = 1; j<=i; j++)
{
dp[i] += dp[j-1]*dp[i-j];
}
}
cout << dp[n] << endl;
}Lets analyse the solution with the help of example..!!

0 1 2 3
| 0 | 0 | 0 | 0 |
|---|
Total UBST's
0 1 2 3
| 1 | 1 | 0 | 0 |
|---|
Total UBST's
0 1 2 3
| 1 | 1 | 1 | 0 |
|---|
Total UBST's
1
2
1
1
0 1 2 3
| 1 | 1 | 1 | 0 |
|---|
Total UBST's
1
2
1
1
1
0
0 1 2 3
| 1 | 1 | 2 | 0 |
|---|
Total UBST's
1
2
1
1
1
0
1
1
1
0 1 2 3
| 1 | 1 | 2 | 0 |
|---|
Total UBST's
1
2
3
0 1 2 3
| 1 | 1 | 2 | 1 |
|---|
Total UBST's
1
2
3
1
0 1 2 3
| 1 | 1 | 2 | 3 |
|---|
Total UBST's
1
2
3
1
2
0 1 2 3
| 1 | 1 | 2 | 3 |
|---|
Total UBST's
1
2
3
1
2
0
2
0 1 2 3
| 1 | 1 | 2 | 5 |
|---|
Total UBST's
1
2
3
1
2
0
2
2
1
2
So the answer for n = 3 will be 5..!!
So that's It for Day 3
Concepts that we have learnt
So that's It for Day 1
We have taken a very first step in Dynamic Programming.
Concepts that we have learnt
1. A small theory of Binary search trees..!!
So that's It for Day 1
We have taken a very first step in Dynamic Programming.
Concepts that we have learnt
1. A small theory of Binary search trees..!!.
2. Using previous combinations stored to calculate present result..!!
Still, Have any Doubts???
Still, Have any Doubts???
Comment it You will get a reply.
OR
Send your doubt to email provided in description.
Copy of Copy of deck
By Chirayu Jain
Copy of Copy of deck
- 83



