Dynamic Programming Series
Dynamic Programming Series
Day 11
LARGEST INDEPENDENT SET
Problem Description
Given a binary tree , find the size of largest independent set?
Problem Description
Given a binary tree , find the size of largest independent set?
What is LIS(Largest Independent Set) ?
Problem Description
Given a binary tree , find the size of largest independent set?
What is LIS(Largest Independent Set) ?
A subset of all tree nodes is an independent set if there is no edge between any two nodes of the subset.
Problem Description
Given a binary tree , find the size of largest independent set?
What is LIS(Largest Independent Set) ?
Example :
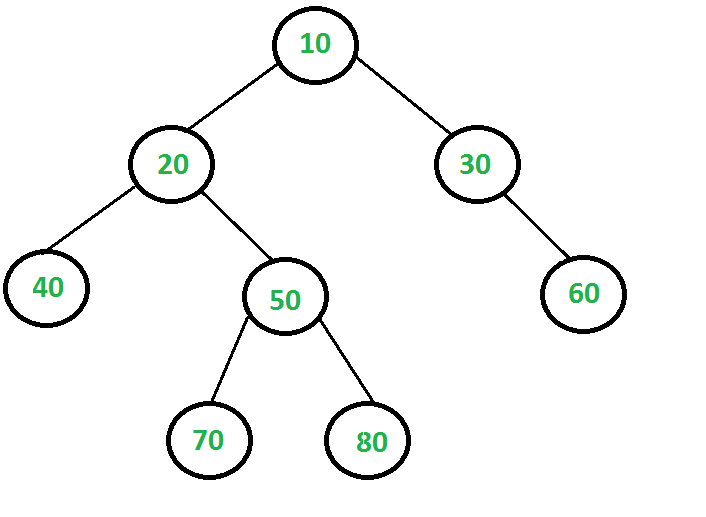
Problem Description

One possible set could be : {10,40,60}
Problem Description

One possible set could be : {10,40,60}
But we have to find the largest?
Problem Description

Here LIS = {10,40,70,80,60}
LENGTH = 5
Problem Description
Now we have understood the problem..!!
The next part consist of the solution and how we need to think about this problem..!!
Problem Description
Now we have understood the problem..!!
The next part consist of the solution and how we need to think about this problem..!!
But before that think about how we can form the solution using same method we followed in dp series..!!
Problem Description
But before that think about how we can form the solution using same method we followed in dp series..!!
1. Making observations.
2. Getting a recursive solution.
3. Applying dynamic programming and reducing time complexity..!!
How To approach this problem?
In the problem it has been given that we cannot have two nodes with common edge..!!
So one thing is clear..!!
How To approach this problem?
In the problem it has been given that we cannot have two nodes with common edge..!!
So one thing is clear..!!
If we include one node than we cannot include its children because they have direct edges..!!
How To approach this problem?
If we include one node than we cannot include its children because they have direct edges..!!
But we can include its grandchildren.!!
These are some perfect observations that we can make..!!
How To approach this problem?
Now this is simple..!!
If we include the node LIS then we can include its grandchildren
How To approach this problem?
Now this is simple..!!
If we include the node LIS then we can include its grandchildren
Otherwise
How To approach this problem?
Now this is simple..!!
If we include the node LIS then we can include its grandchildren
Otherwise
We can include its children..!!

How To approach this problem?
For a node X we can say
How To approach this problem?
For a node X we can say
LIS(X) = max {( 1 + sum of LIS (grandchildren of X)), (sum of LIS(children of X))}
We have developed a recursive approach
How To approach this problem?
We can see that there are lot of repititive sub problems in this recursive approach..!!
10
30
20
50
40
60
70
How To approach this problem?
We can see that there are lot of repititive sub problems in this recursive approach..!!
10
30
20
50
40
60
70
For calculating LIS of 10 we need to know LIS of its children and grandchildren.
How To approach this problem?
We can see that there are lot of repititive sub problems in this recursive approach..!!
10
30
20
50
40
60
70
For calculating LIS of 20 we need to know LIS of its children and grandchildren.
How To approach this problem?
Now what we can do is..!!
At a particular node we can store the LIS value of that node in it..!! Rather than just computing the value again and again..!!
Lets see the coding part of the problem..!!
How To approach this problem?
int LIS(node *root)
{
if (root == NULL)
return 0;
if (root->lis)
return root->lis;
if (root->left == NULL && root->right == NULL)
{
root->lis = 1;
return root->lis;
}
int lis_child = LIS(root->left) + LIS(root->right);
int lis_grand_child = 1;
if (root->left)
lis_granc_child += LIS(root->left->left) + LIS(root->left->right);
if (root->right)
lis_grand_child += LIS(root->right->left) + LIS(root->right->right);
root->lis = max(lis_child , lis_grand_child);
return root->lis;
} So that's It for Day 11
One task for you guys..!!
One task for you guys..!!
In this particular problem why are we not adding up the values at even and odd levels of the tree and returning the max of it?
One task for you guys..!!
In this particular problem why are we not adding up the values at even and odd levels of the tree and returning the max of it?
Do comment your answer in the comment section..!! Lets see where our conceptual knowledge is.. :)
So that's It for Day 10
Concepts that we have learnt
So that's It for Day 10
We have taken a very first step in Dynamic Programming.
Concepts that we have learnt
1. DP in trees
So that's It for Day 10
We have taken a very first step in Dynamic Programming.
Concepts that we have learnt
1. DP in trees.
2. Memoization in trees.
So that's It for Day 10
We have taken a very first step in Dynamic Programming.
Concepts that we have learnt
1. DP in trees.
2. Memoization in trees.
Still, Have any Doubts???
Still, Have any Doubts???
Comment it You will get a reply
OR
Send your doubt to email provided in description.
Copy of Copy of Distinct Subsequences
By Chirayu Jain
Copy of Copy of Distinct Subsequences
- 113



