pollev.com/chrismakler
When is the first homework due?
Characteristics of
Production Functions
Christopher Makler
Stanford University Department of Economics
Econ 50: Lecture 3
Goal for Today: Analyze how different functional forms can be used to model different production processes
Examples of Production Functions
f(L,K) = aL + bK
Linear
f(L,K) = \min\{aL, bK\}
Leontief
(Fixed Proportions)
Cobb-Douglas
f(L,K) = AL^aK^b
Constant Elasticity of Substitution (CES)
f(L,K) = (aL^\rho + bK^\rho)^{1 \over \rho}
Story
f(L,K) = 2L + 4K
If Chuck uses his bare hands (L), he can catch 2 fish per hour.
If Chuck uses a net (K),
he can collect 4 fish per net.
Model
Fish from L hours of labor = 2L
Fish from K nets = 4K
How many fish can he produce altogether if he uses
L hours of labor, and K nets?
f(L,K) = 2L + 4K
If Chuck uses his bare hands (L), he can catch 2 fish per hour.
If Chuck uses a net (K),
he can collect 4 fish per net.
MP_L = {df \over dL} = 2 {\text{fish} \over \text{hour}}
MP_K = {df \over dK} = 4 {\text{fish} \over \text{net}}
MRTS =
= {\text{1 net} \over \text{2 hours}}
Intuition: no matter how many hours he works, and how many nets he uses,
he can catch the same number of fish with 1 net as he can using 2 hours of labor.
f(L,K) = 2L + 4K
If Chuck uses his bare hands (L), he can catch 2 fish per hour.
If Chuck uses a net (K),
he can collect 4 fish per net.
MRTS = {\text{1 net} \over \text{2 hours}}
What does an isoquant look like?
What does the isoquant for \(q = 20\) look like?
L
K
Linear Production Function
MP_L =
MP_K =
MRTS =
\displaystyle{a\ {\text{output} \over \text{unit of L}}}
\displaystyle{b\ {\text{output} \over \text{unit of K}}}
\displaystyle{= {a \text{ units of K} \over b \text{ units of L}}}
q=f(L,K)=aL + bK
Linear Production Function
\displaystyle{MRTS = {a \text{ units of K} \over b \text{ units of L}}}
q=f(L,K)=aL + bK
What happens to an isoquant if \(a\) increases?
L
K
Story
f(2,1) = 16
Two workers and a garbage truck can collect 16 bins per hour.
Adding a worker or getting an extra truck doesn't help.
Model
However, if you get another truck and two more workers, you can collect another 16 bins.
f(3,1) = 16
f(2,2) = 16
f(4,2) = 32
If you have more than twice as many workers as trucks,
your production depends on the number of trucks you have.
If you have less than twice as many workers as trucks,
your production depends on the number of workers you have.
L \le 2K
L \ge 2K
\Rightarrow q = 8L
\Rightarrow q = 16K
f(L,K)=\begin{cases}8L & \text{ if }L \le 2K\\16K & \text{ if }L \ge 2K\end{cases}
=\min\{8L,16K\}
MP_L=\begin{cases}8 & \text{ if }L \le 2K\\0 & \text{ if }L \ge 2K\end{cases}
MP_K=\begin{cases}0 & \text{ if }L \le 2K\\16 & \text{ if }L \ge 2K\end{cases}
=\begin{cases}\infty & \text{ if }L \le 2K\\0 & \text{ if }L \ge 2K\end{cases}
MRTS =
If you have more than twice as many workers as trucks,
your production depends on the number of trucks you have.
If you have less than twice as many workers as trucks,
your production depends on the number of workers you have.
L \le 2K
L \ge 2K
\Rightarrow q = 8L
\Rightarrow q = 16K
Leontief Production Function
\displaystyle{MRTS = \begin{cases}\infty & \text{ if }L \le 2K\\0 & \text{ if }L \ge 2K\end{cases}}
q=f(L,K)=\min\{8L, 16K\}
What do the isoquants look like?
L
K
Leontief (Fixed Proportions) Production Function
f(L,K)=\begin{cases}aL \text{\ \ if }aL \le bK\\bK \text{\ \ if }aL \ge bK\end{cases}
=\min\{aL,bK\}
MP_L =
MP_K =
MRTS =
\begin{cases}a \text{\ \ if }aL < bK\\0 \text{\ \ if }aL > bK\end{cases}
\begin{cases}0 \text{\ \ if }aL < bK\\b \text{\ \ if }aL > bK\end{cases}
= \begin{cases}\infty \text{\ \ if }aL < bK\\0 \text{\ \ if }aL > bK\end{cases}
f(L,K) = \min\{2L, K\}
Cobb-Douglas Production Function
q=f(L,K)=AL^aK^b
MP_L = aAL^{a-1}K^b
MP_K = bAL^aK^{b-1}
MRTS =
\displaystyle{= {a \over b} \times {K \over L}}
Cobb-Douglas Production Function
q=f(L,K)=L^{1\over 2}K^{1 \over 4}
What does the isoquant for \(q = 4\) look like?
MRTS = {2K \over L}
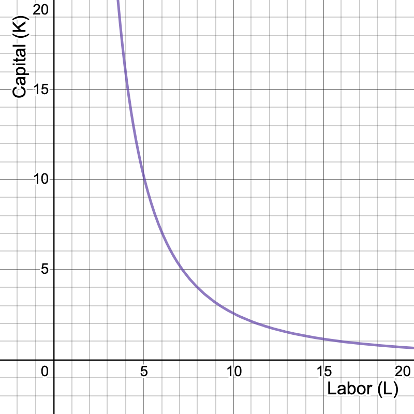
CES Production Function
q=f(L,K)=(aL^\rho + bK^\rho)^{1 \over \rho}
\displaystyle{MRTS= {a \over b} \times \left({K \over L}\right)^{1-\rho}}
MRTS for Different Production Functions
aL + bK
Linear
\min\{aL, bK\}
Leontief
(Fixed Proportions)
Cobb-Douglas
AL^aK^b
CES
(aL^\rho + bK^\rho)^{1 \over \rho}
f(L,K)
MRTS
\frac{a}{b}
\begin{cases}\infty \text{\ \ if }aL < bK\\0 \text{\ \ if }aL > bK\end{cases}
\frac{a}{b}\times \frac{K}{L}
\frac{a}{b}\times \left(\frac{K}{L}\right)^{1-\rho}
Elasticity of Substitution
- Measures the substitutability of one input for another
- Key to answering the question: "will my job be automated?"
- Formal definition: the inverse of the percentage change in the MRTS
per percentage change in the ratio of capital to labor, K/L - Intuitively: how "curved" are the isoquants for a production function?
Scaling Production
How does a technology respond to increasing production?
Short run: only some resources can be reallocated
Long run: all resources can be reallocated
It depends on the time horizon:
Scaling Production in the Short Run
Suppose \(K\) is fixed at some \(\overline K\) in the short run.
Then the production function becomes \(f(L\ |\ \overline K)\)
pollev.com/chrismakler
When does the production function
f(L) = 10L^a
exhibit diminishing marginal product of labor?
Scaling Production in the Long Run
What happens when we increase all inputs proportionally?
For example, what happens if we double both labor and capital?
Does doubling inputs -- i.e., getting \(f(2L,2K)\) -- double output?
f(2L,2K) > 2f(L,K)
f(2L,2K) = 2f(L,K)
f(2L,2K) < 2f(L,K)
Decreasing Returns to Scale
Constant Returns to Scale
Increasing Returns to Scale
f(L,K) = 4L^{1 \over 2}K
Does this exhibit diminishing, constant or increasing MPL?
Does this exhibit decreasing, constant or increasing returns to scale?
pollev.com/chrismakler
When does the production function
f(L,K) = AL^aK^b
exhibit constant returns to scale?
Next Steps
- Homework for today's class is due on Saturday night
- Readings and quizzes for next week have been posted
- Homework for next week will be posted later today
Econ 50 | Lecture 03
By Chris Makler
Econ 50 | Lecture 03
Characteristics of Production Functions
