pollev.com/chrismakler
Suppose Chuck can use labor
to produce fish (good 1)
or coconuts (good 2).
If we plot his PPF in good 1 - good 2 space, what are the units of Chuck's MRT?
Christopher Makler
Stanford University Department of Economics
Econ 50: Lecture 4
Resource Constraints and Production Possibilities
Today's Agenda
Part 1: From production functions to the PPF
Part 2: The slope of the PPF
Getting situated in "Good 1 - Good 2 space"
Resource constraints and the PPF
Deriving the equation of the short-run PPF
Shifts in technology and the long-run PPF
The Marginal Rate of Transformation
Relationship between MPL and MRT
Deriving the expression for the MRT
using the implicit function theorem
Good 1 - Good 2 Space
x_1
x_2
Two "Goods" (e.g. fish and coconuts)
A bundle is some quantity of each good
\text{Bundle }X = (x_1,x_2)
x_1 = \text{quantity of good 1 in bundle }X
x_2 = \text{quantity of good 2 in bundle }X
Can plot this in a graph with \(x_1\) on the horizontal axis and \(x_2\) on the vertical axis
A = (4,16)
B = (8,8)
A
B
4
8
12
16
20
4
8
12
16
20
Good 1 - Good 2 Space
x_1
x_2
What tradeoff is represented by moving
from bundle A to bundle B?
\text{Give up }\Delta x_2 =
A
B
4
8
12
16
20
4
8
12
16
20
\text{Gain }\Delta x_1 =
\text{Rate of exchange }=
ANY SLOPE IN
GOOD 1 - GOOD 2 SPACE
IS MEASURED IN
UNITS OF GOOD 2
PER UNIT OF GOOD 1
ANY SLOPE IN
GOOD 1 - GOOD 2 SPACE
IS MEASURED IN
UNITS OF GOOD 2
PER UNIT OF GOOD 1
TW: HORRIBLE STROBE EFFECT!
Multiple Uses of Resources
Labor
Fish
🐟
Coconuts
🥥
[GOOD 1]
⏳
[GOOD 2]
L_1
L_2
\overline L
Resource Constraint
L_1
L_2
L_1 + L_2 = \overline L
\overline L
\overline L
\text{Total labor available }=\overline L
Production Possibilities
\text{Fish }(x_1)
\text{Coconuts }(x_2)
Resource Constraint
L_1
L_2
L_1 + L_2 = \overline L
\overline L
\overline L
\text{Total labor available }=\overline L
\text{(Good 1 - Good 2 space)}
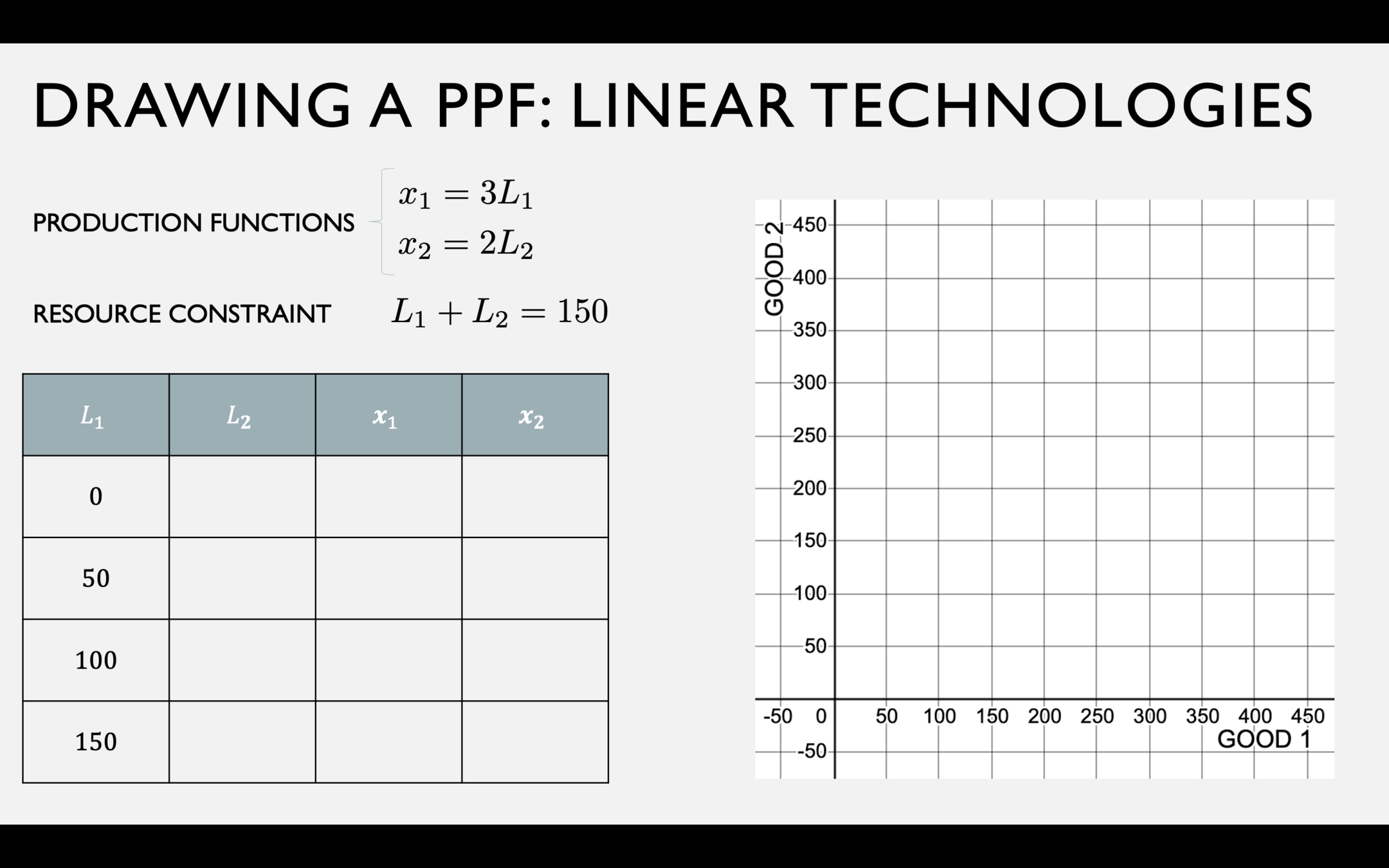
A PPF with Linear Technologies
x_1 = f_1(L_1) = 3L_1
x_2 = f_2(L_2) = 2L_2
Fish production function
Coconut production function
Resource Constraint
L_1 + L_2 = 150
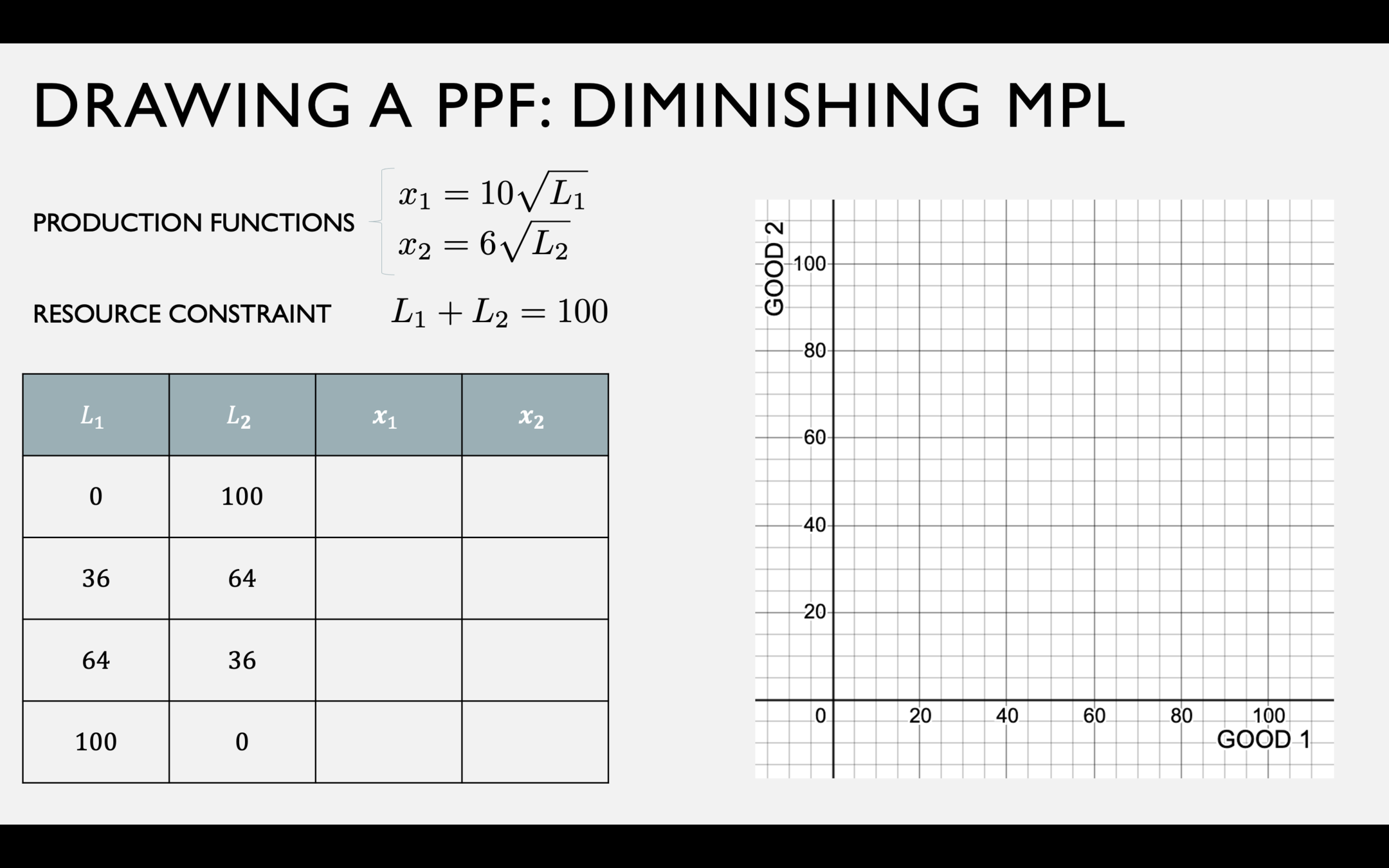
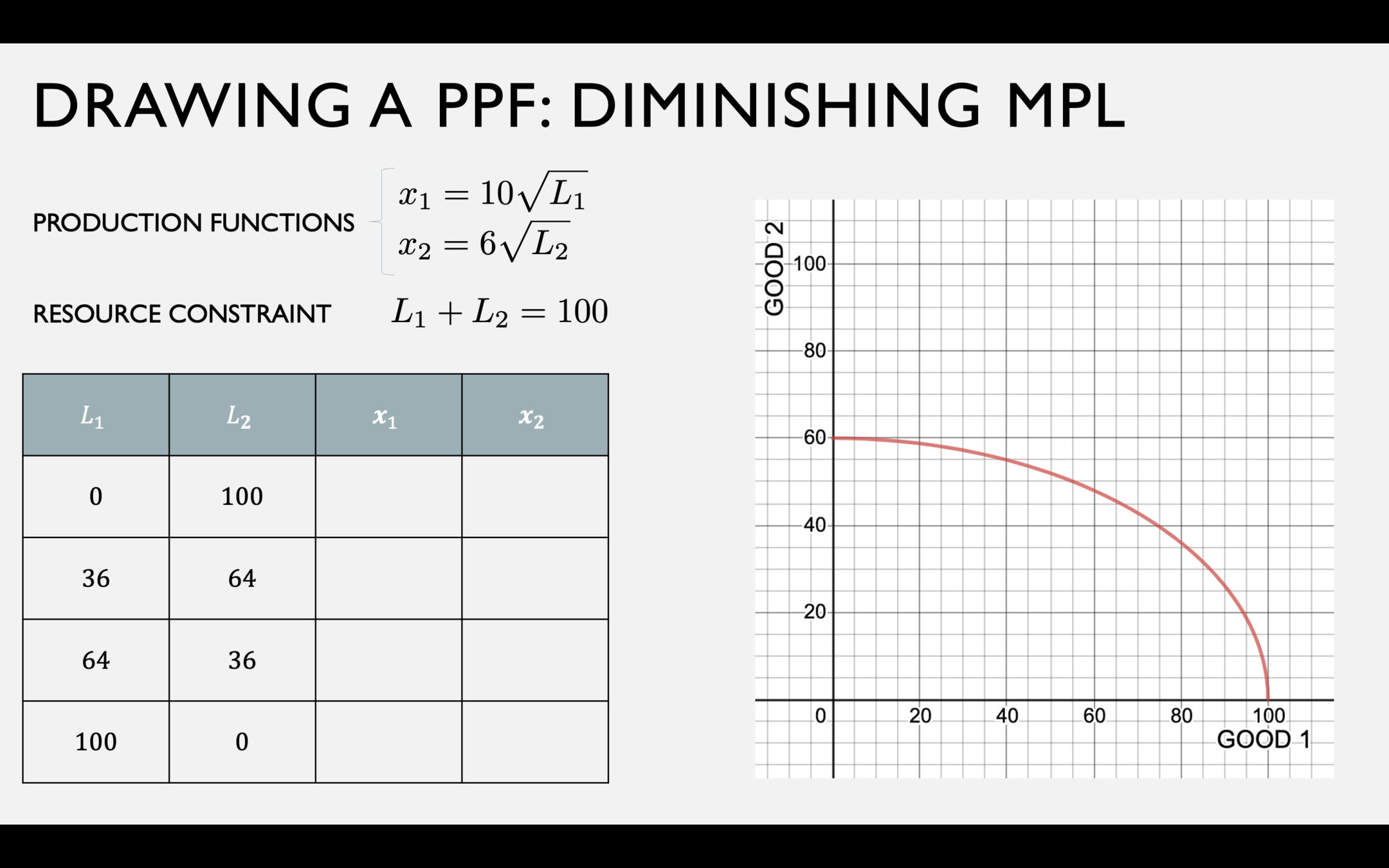
A PPF with Diminishing \(MP_L\)
x_1 = f_1(L_1) = 10\sqrt{L_1}
x_2 = f_2(L_2) = 6\sqrt{L_2}
Fish production function
Coconut production function
Resource Constraint
L_1 + L_2 = 100
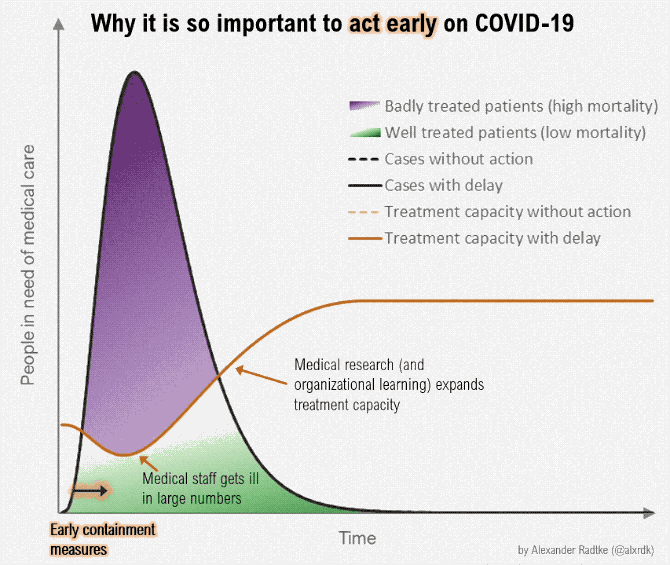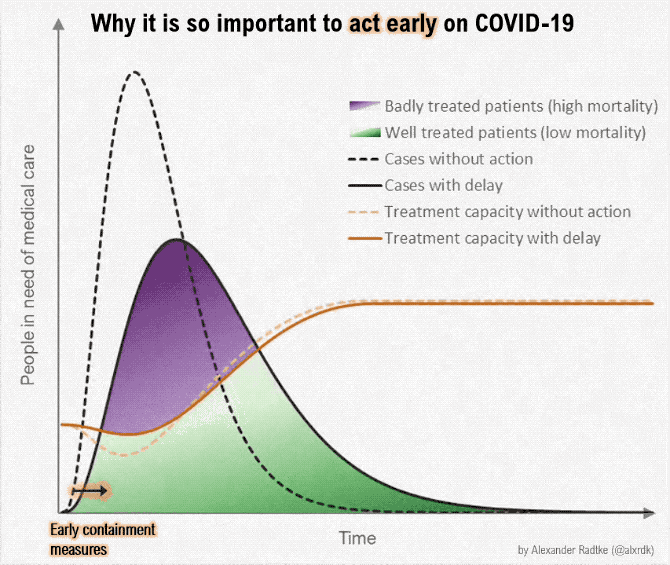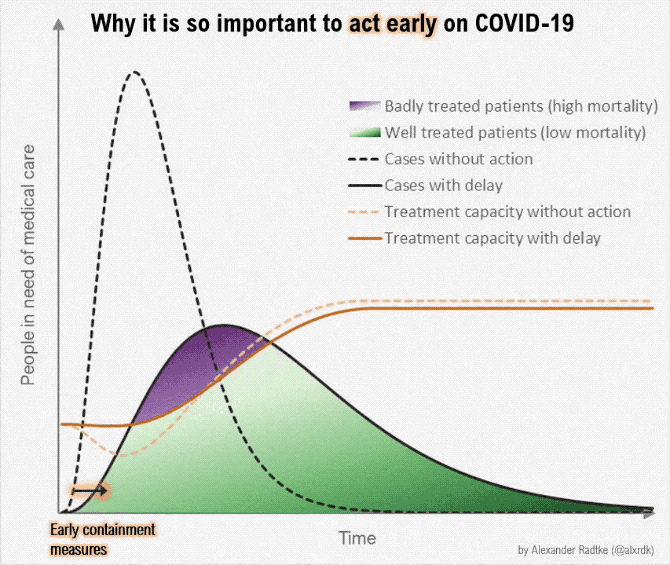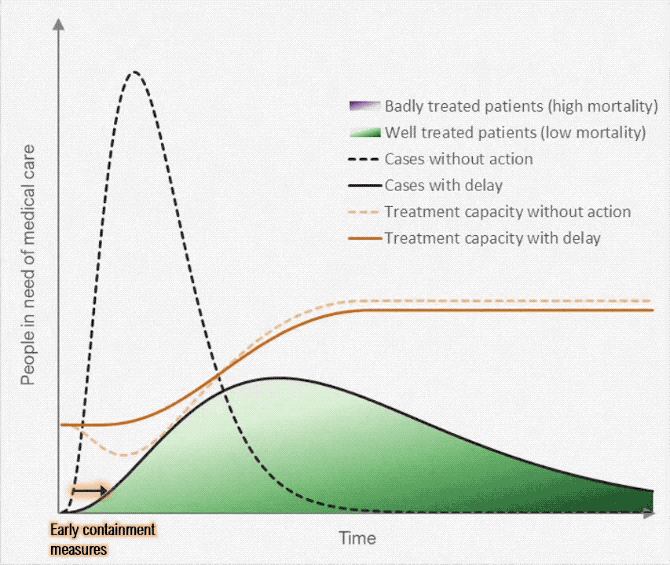
- Suppose we want to produce a lot more of something -- ventilators, masks, toilet paper, hand sanitizer
- Some resources can be reallocated quickly; others are more specialized and can't be quickly repurposed
- How can we "scale up" in the short run and the long run?
- How do short-run tradeoffs compare with long-run tradeoffs?
Shifts in the PPF
f_1(L_1) = {5 \over 4}\sqrt{L_1K_1}
f_2(L_2) = \sqrt{L_2K_2}
Consider an economy with \(\overline L = 100\) units of labor and \(\overline K = 100\) units of capital.
In the short run, \(K_1 = 64\) and \(K_2 = 36\).
In the long run, capital can be reallocated in any combination between goods 1 and 2.
Max in SR
Max in LR
- Up to now: how a short-run PPF can shift due to changing the allocation of capital, holding production functions constant.
- What happens when the technology itself (i.e. the production function) changes?
Improvements in Technology
The New York Times, Oct. 29, 2013
Insider, July 23, 2020
f_1(L_1) = A_1\sqrt{L_1K_1}
f_2(L_2) = A_2\sqrt{L_2K_2}
Consider an economy with \(\overline L = 100\) units of labor and \(\overline K = 100\) units of capital.
In the short run, \(K_1 = 64\) and \(K_2 = 36\).
In the long run, capital can be reallocated in any combination between goods 1 and 2.
Max in SR
Max in LR
Part 2: The MRT
Slope of the PPF:
Marginal Rate of Transformation (MRT)
Rate at which one good may be “transformed" into another
...by reallocating resources from one to the other.
Opportunity cost of producing an additional unit of good 1,
in terms of good 2
Note: we will generally treat this as a positive number
(the magnitude of the slope)
Suppose we're allocating 100 units of labor to fish (good 1),
and 50 of labor to coconuts (good 2).
Now suppose we shift
one unit of labor
from coconuts to fish.
How many fish do we gain?
\Delta_2
\Delta_1
100
98
300
303
How many coconuts do we lose?
\Delta_2 = MP_{L_2} = 2\text{ coconuts}
\Delta_1 = MP_{L_1} = 3\text{ fish}
\left|\text{slope}\right| = \frac{MP_{L_2}}{MP_{L_1}}
Relationship between MPL's and MRT
x_1 = f_1(L_1) = 3L_1
x_2 = f_2(L_2) = 2L_2
Fish production function
Coconut production function
Resource Constraint
L_1 + L_2 = 150
PPF
Suppose Chuck could initially produce 3 fish (good 1) or 2 coconuts (good 2)
in an hour.
He gets better at fishing, which allows him to produce 4 fish per hour.
What effect will this have on his MRT?
CHECK YOUR UNDERSTANDING
pollev.com/chrismakler
Diminishing \(MP_L\)'s
and Increasing \(MRT\)
Important Notes
The MRT is the slope of the PPF at some output combination \((x_1,x_2)\)
You should therefore write it in terms of \(x_1\) and \(x_2\), not \(L_1\) and \(L_2\).
You can use two methods to find the MRT:
the ratio of the MPL's, or the implicit function theorem.
CHECK YOUR UNDERSTANDING
Chuck has \(\overline L = 8\) total hours of labor,
and the production functions
\(x_1 = 2 \sqrt{L_1}\) and \(x_2 = 4\sqrt{L_2}\).
What is his MRT if he spends
half his time producing each good?
pollev.com/chrismakler
CHECK YOUR UNDERSTANDING
Charlene has the PPF given by
\(2x_1^3 + 3x_2^4 = 1072\)
What is her MRT if she produces the output combination \((8,2)\)?
pollev.com/chrismakler
- Resource constraints + production functions = production possibilities
- The MRT (slope of PPF) is the opportunity cost of producing good 1
(in terms of good 2) - If there is only one input (labor), the MRT is the ratio of the MPL's
- In general, best way to find the MRT is by using the implicit function theorem
- Homework due Thursday night
- Next topic: preferences over bundles
Key Takeaways
Econ 50 | Spring 23 | Lecture 4
By Chris Makler
Econ 50 | Spring 23 | Lecture 4
Resource Constraints and Production Possibilities
