Production Functions with Multiple Inputs
Christopher Makler
Stanford University Department of Economics
Econ 50: Lecture 3
Resources
Technology
Stuff
Happiness
🌎
🏭
⌚️
🤓
Part I: The Real Economy
UNIT I: PRODUCTION FUNCTIONS
UNIT II: UTILITY FUNCTIONS
Lecture 2
Production functions with one input
PPFs with
one input
Lecture 3
Lecture 4
Production functions with multiple inputs
Short-run and
long-run PPFs
Theme of Econ 50
Relationship between
mathematical representation,
graphical representations,
and economic concepts
Key Mathematical Concepts
Functional Forms
of multivariate functions
Marginal products
as partial derivatives
Key Graphical Concepts
Level sets
(isoquants)
Slopes of level sets
(MRTS)
Key Economic Concepts
Productivity of Labor and Capital
Substitutability of Labor and Capital
Today's Agenda
- Production functions
- UCSD 4.1(a) from 2:40
- Marginal products
- UCSD 4.1(d) and (f)
- Isoquants and their slopes
- UCSD 4.1(h-k)
- Substitutability of Inputs
Substitutability of Inputs
Why Different Functional Forms?
- Realism
- Policy implications
Interpreting the MRTS
(slope of an isoquant)
"What is the rate at which
one can substitute
one input for another
and keep output the same?"
Another way of thinking about it:
"If we fired one worker and wanted to keep output the same,
how many additional machines would we need to buy?"
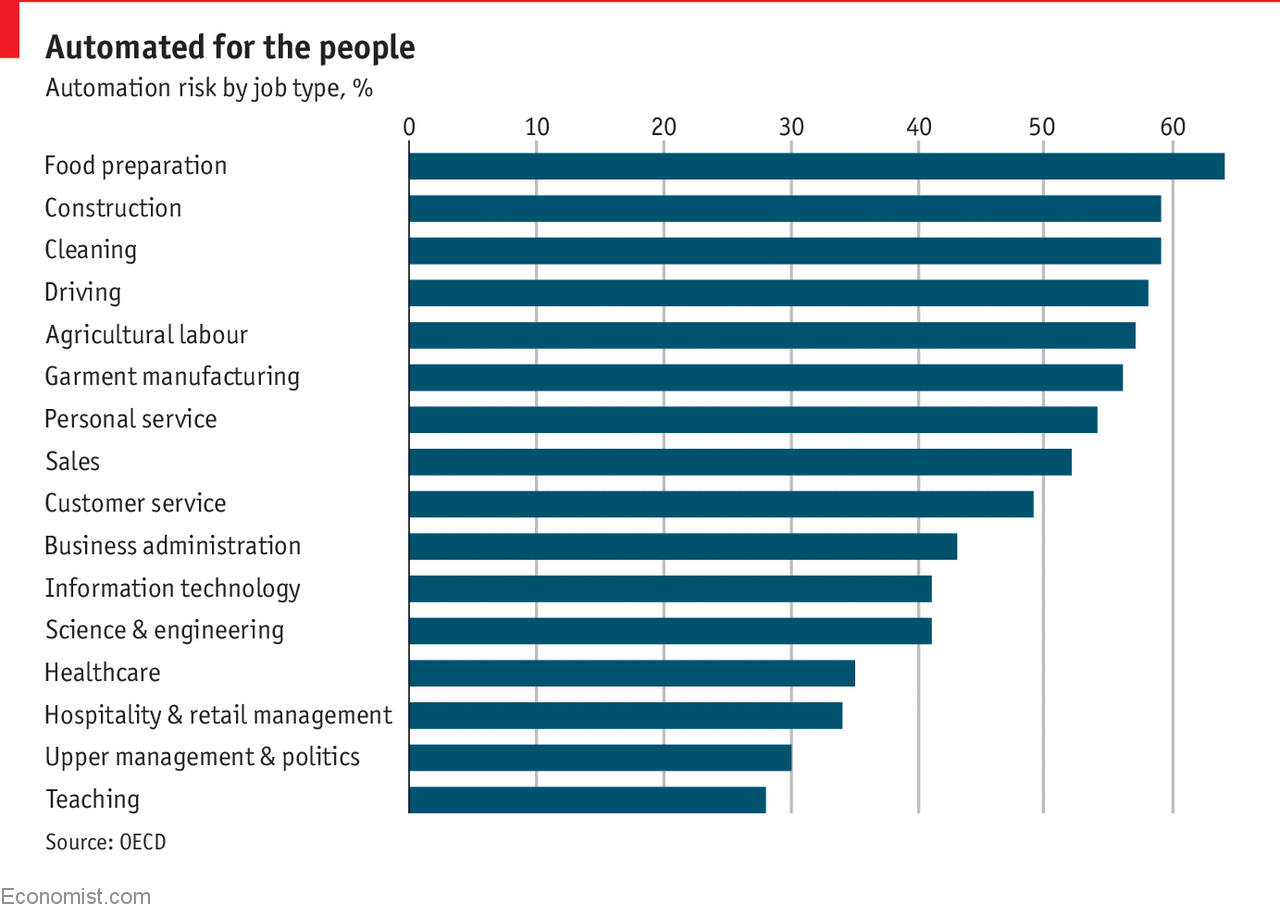
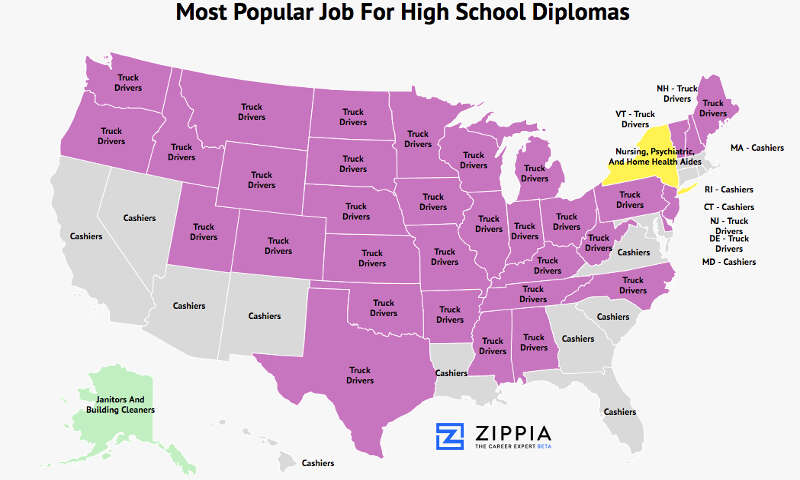
According to the Bureau of Labor Statistics,
truck driver is the #1 job
for people with a High School diploma
Elasticity of Substitution
- Measures the substitutability of one input for another
- Key to answering the question: "will my job be automated?"
\(L\)
\(K\)
Leontief
(Fixed Proportions)
f(L,K) = \min\left\{L,K\right\}
Have to use labor and capital together
\(L\)
\(K\)
Linear
(Perfect Substitutes)
f(L,K) = L + K
Can replace one worker with one unit of capital
CES Production Function
Parameter \(\rho\) describes the substitutability of L and K
f(L,K) = (L^\rho + K^\rho)^\frac{1}{\rho}
Next Time
How can we draw a production possibilities frontier
for production functions with multiple inputs?
New concepts:
returns to scale and short-run/long-run.
Econ 50V | 3 | Production Functions with More Than One Input
By Chris Makler
