Public Goods
and Public Choice
Christopher Makler
Stanford University Department of Economics
Econ 51: Lecture 8
Today's Agenda
Hour 1: Optimal Provision
Hour 2: Social Choice
Classifying goods: rival/excludable
When to provide a public good
How much of a public good to provide
Funding mechanisms
Voluntary contribution and Free Riding
Voting over public goods
Classifying Goods
Rivalry in Consumption
One agent's consumption affects others' ability to consume it the same good.
Excludability
Agents may be prevented from consuming the good
Rival
Nonrival
Excludable
Nonexcludable
Private Goods
Common Resources
Public Goods
Club Goods
These aren't hard-and-fast categories
- Interstate 280 at 4am is a public good (nonrival, nonexcludable)
- Interstate 280 at 4pm is a common resource (rival, nonexcludable)
When to Provide a Public Good
How Much Public Good to Provide
Private goods: aggregate preferences by summing demand curves horizontally.
Public goods: aggregate preferences by summing demand curves vertically.
Since the demand curve represents the MRS, this means the efficient amount to produce is where the sum of the MRS's equals the cost.
Model 2: A Fireworks Show
A town is preparing to have a fireworks show.
Let \(G\) be the total number of minutes of fireworks
Let \(g_i \ge 0\) be the amount citizen \(i\) contributes to the show.
Each minute of fireworks costs $200.
There are two types of citizen:
200 kinda love fireworks
u(G, x_i) = 12\sqrt G + x_i
u(G, x_i) = 4\sqrt G + x_i
Note: \(x_i\) is private consumption (dollars left over after contributing \(g_i\)) so we can also write
u(G, g_i) = 12\sqrt G - g_i
u(G, g_i) = 4\sqrt G - g_i
100 really love fireworks
\(G\) = total number of minutes of fireworks
\(g_i \ge 0\) = amount citizen \(i\) contributes
Each minute of fireworks costs $200
There are two types of citizen:
100 really love fireworks
200 kinda love fireworks
u(G, g_i) = 12\sqrt G - g_i
u(G, g_i) = 4\sqrt G - g_i
Questions:
What is the efficient length of a fireworks show?
What is the fairest way to pay for the fireworks?
How can the town decide how long of a show to have?
\(G\) = total number of minutes of fireworks
\(g_i \ge 0\) = amount citizen \(i\) contributes
100 really love fireworks
200 kinda love fireworks
u(G, g_i) = 12\sqrt G - g_i
u(G, g_i) = 4\sqrt G - g_i
What is the efficient length of a fireworks show?
MB = {6 \over \sqrt{G}}
MB = {2 \over \sqrt{G}}
Cost
200G
MC = 200
"Samuelson Condition" : set the sum of the MB's equal to the MC:
100 \times {6 \over \sqrt{G}}
+
=
200 \times {2 \over \sqrt{G}}
200
G^* = 25
\(G\) = total number of minutes of fireworks
\(g_i \ge 0\) = amount citizen \(i\) contributes
100 really love fireworks
200 kinda love fireworks
u(G, g_i) = 12\sqrt G - g_i
u(G, g_i) = 4\sqrt G - g_i
What is the efficient length of a fireworks show?
MB = {6 \over \sqrt{G}}
MB = {2 \over \sqrt{G}}
Cost
200G
MC = 200
Suppose everyone else had contributed some amount \(G\).
How much would each type voluntarily contribute?
For example, suppose everyone else had contributed enough for a 4-minute-long show.
What is the marginal benefit of each type?
This is called the free rider problem.
\(G\) = total number of minutes of fireworks
\(g_i \ge 0\) = amount citizen \(i\) contributes
100 really love fireworks
200 kinda love fireworks
u(G, g_i) = 12\sqrt G - g_i
u(G, g_i) = 4\sqrt G - g_i
What mechanism can achieve the efficient quantity of \(G^* = 25\)?
Cost
200G
Suppose you knew everyone's type, and could charge them differently.
You could charge everyone half their valuation:
$30 for people who love fireworks, $10 for people who kinda love fireworks.
u(25, g_i) = 60 - g_i
u(25, g_i) = 20 - g_i
5000
What's the problem with this?
\(G\) = total number of minutes of fireworks
\(g_i \ge 0\) = amount citizen \(i\) contributes
100 really love fireworks
200 kinda love fireworks
u(G, g_i) = 12\sqrt G - g_i
u(G, g_i) = 4\sqrt G - g_i
Suppose people voted on the fireworks show. There are 300 people, so \(G = 300g/200 = 3g_i/2\)
u(g_i) = 12\sqrt{{3 \over 2}g_i} - g_i
u(g_i) = 4\sqrt{{3 \over 2}g_i} - g_i
g_i^* = 81
g_i^* = 9
What would a majority vote for?
Social Choice
To navigate: press "N" to move forward and "P" to move back.
To see an outline, press "ESC". Topics are arranged in columns.
Big Ideas
We're going from individual choice to social choice.
Up to now we've had an individual agent choosing something.
Societies also make choices: how much to tax and spend, who to lead them, etc.
How do we evaluate mechanisms for aggregating preferences?
It's "impossible" to find an aggregation method that works in general.
However, under certain more restrictive assumptions on preferences,
some mechanisms will work better than others, with predictable outcomes.
From Social Preferences to Social Choice
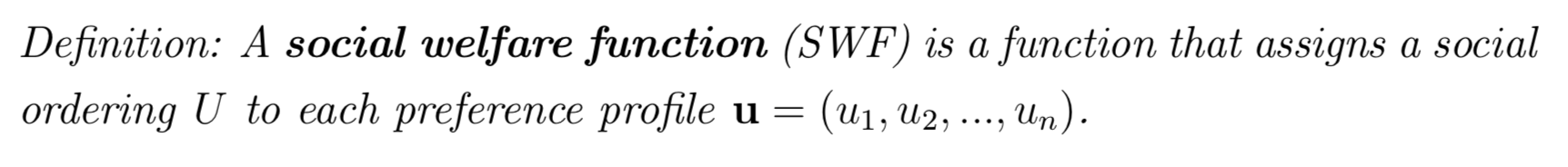
Terminology
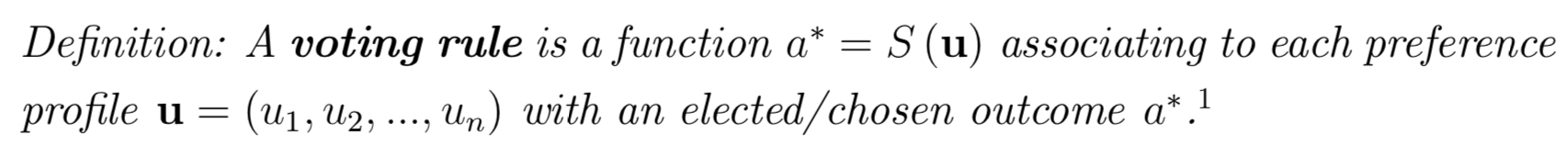
A SWF ranks all possible alternatives:
e.g., has indifference curves within the Edgeworth Box
Just needs to pick a winner;
sometimes called a Social Choice Function (SCF)
Arrow's Impossibility Theorem
Desirable Properties of a Social Welfare Function
- Non-dictatorship: it isn't just simply the preferences of one dictator.
- Unanimity: if everyone likes A better then B, then society cannot prefer B to A.
- Independence of Irrelevant Alternatives: if society prefers A to B when C isn't an option, it cannot prefer B to A when C is an option.
Arrow's Theorem: There is no complete and transitive SWF that satisfies all three of these.
Example: Failure of Majority Rule
Ana, Beth, and Claudia are buying a television.
They can buy an RCA (R), Sony (S), or Toshiba (T).
Their preference rankings are given by the following:
Suppose we were to create a social preference ordering by pairwise ranking each alternative, choosing the preferred one by majority rule.
Then society prefers R to S...
and S to T...
and T to R...
which isn't transitive!
Another Mechanism: Borda Count
Let's assign a point value to your choice ranking:
Now we see that this is a tie: each gets 6 points.
But now let's look to see what happens if there's a fourth option, a Zenith:
Now R has 6 points, but S and T have 7. So the introduction of Z changes the preferences over
R, S, T => violates the independence of irrelevant alternatives axiom.
The Condorcet Paradox
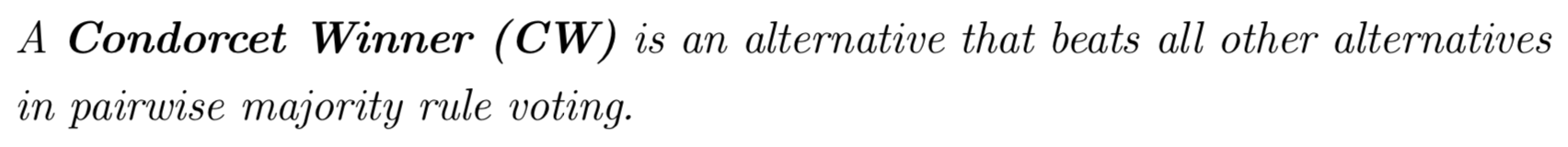
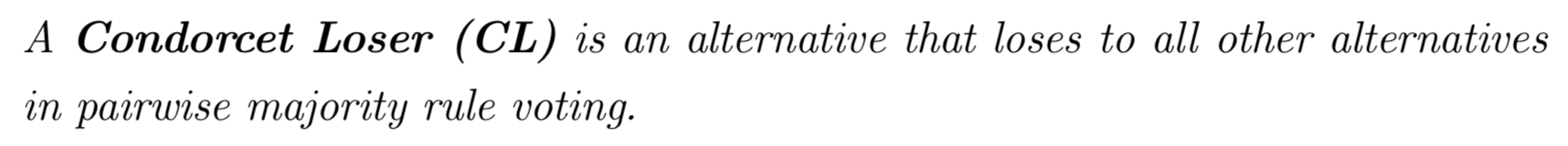
As in the TV question, a CW or CL may not always exist, which can result in a voting cycle!
If you set the voting rule,
you can choose the winner.
| Voting Rule | Winner |
|---|---|
| S vs T, then winner vs. R | R |
| R vs T, then winner vs. S | S |
| S vs R, then winner vs. T | T |
I do not expect you to solve a VCG problem on the final exam; however, it is fair game to ask what problem it is trying to solve,
and its approach to solving that problem.
Note
The VCG Mechanism
General class of problems: a group of people with
private information has to make a collective choice.
For example: suppose three roommates are moving into a new apartment,
so there are 6 possible ways they could be assigned to rooms.
They each have preferences over all 6 possible combinations.
How can they decide who gets which room?
General Formulation
There are people \(i = 1,...,N\) and possible decisions \(k = 1,...,K\).
Person \(i\) would get payoff \(v_{ik}\) if option \(k\) is chosen.
The goal is to collect accurate information about individual values and pick the decision \(k^*\) that maximizes the total value:
A direct mechanism asks each person to report their values for each outcome and select the one that maximizes total welfare.
\(W(k) = v_{1k} + \cdots + v_{Nk}\)
Each player can, by its report, force the selection of any outcome, so why would it always choose \(k^*\)?
Goal: align payoffs of individuals with the total social payoff.
Mechanism: define a series of transfer payments based on stated valuations that encourage truthful revelation of value.
Vickrey-Clarke-Groves Mechanism
1. Each player reports their vector of values for each of the \(K\) alternatives: \(v_i = (v_{i1}, ... , v_{iK})\). They can lie if they want.
3. When the "center" chooses \(k\), it pays player \(i\):
Analysis of incentives: player \(i\) wants to induce the center to choose the \(k\) that maximizes:
2. The "center" selects the \(k^*\) that maximizes the total reported value.
\displaystyle{p_i(k) = \sum_{j \ne i} v_{jk} + f_n(v_{-i})}
v_{ik} + p_i(k, v_{-i})
\displaystyle{= v_{ik} + \sum_{j \ne i} v_{jk} + f_n(v_{-i})}
They do this by reporting truthfully!
A player is said to be pivotal when its reported vector of values
changes the outcome of the mechanism,
compared to the case in which they didn't participate
(i.e., reported just a vector of zeroes).
In a pivot mechanism, only the pivotal players have a side payment.
In particular, they have to pay the amount
by which they change other people's (reported) utility.
Econ 51 | 21 | Public Goods
By Chris Makler
