Oligopoly, Part II
Christopher Makler
Stanford University Department of Economics
Econ 51: Lecture 8
Review of Last Time
Simple case: linear demand, constant MC, no fixed costs
P(Q) = 14 - Q
c(Q) = 2Q
\text{No fixed costs }\Rightarrow MC = AC = 2
Baseline Example: Monopoly
P(Q) = 14 - Q
c(Q) = 2Q
\pi(Q) = P(Q)Q - c(Q)
= (14 - Q)Q - 2Q
= 14Q - Q^2 - 2Q
\text{total revenue}
\text{total cost}
14
2
units
$/unit
P(Q) = 14 - Q
MC = AC = 2
\text{No fixed costs }\Rightarrow MC = AC = 2
14
P
Q
Baseline Example: Monopoly
P(Q) = 14 - Q
c(Q) = 2Q
\pi(Q) = P(Q)Q - c(Q)
= (14 - Q)Q - 2Q
= 14Q - Q^2 - 2Q
\text{total revenue}
\text{total cost}
14
2
units
$/unit
P(Q) = 14 - Q
MC = AC = 2
\text{No fixed costs }\Rightarrow MC = AC = 2
14
P
Q
Profit
Baseline Example: Monopoly
P(Q) = 14 - Q
c(Q) = 2Q
\pi(Q) = P(Q)Q - c(Q)
= (14 - Q)Q - 2Q
= 14Q - Q^2 - 2Q
\pi'(Q) = 14 - 2Q - 2 = 0
Q^* = 6
\text{total revenue}
\text{total cost}
\text{marginal revenue}
\text{marginal cost}
P^* = 14 - 6 = 8
\pi^* = 8\times 6 - 2 \times 6 = 36
14
8
2
6
Q
P
P(Q) = 14 - Q
MR(Q) = 14 - 2Q
MC = AC = 2
36
Quantity Duopoly
- Two firms ("duo" in duopoly)
- Each chooses how much to produce
- Market price depends on
the total amount produced - Each firm faces a residual demand curve
based on the other firm's choice
Quantity Leadership Model
- Firm 1 chooses how much to produce first \(q_1\),
at a cost of $2 per unit - Firm 2 observes firm 1's choice,
and then chooses how much to produce \(q_2\),
also at a cost of $2 per unit - The market price is determined by \(P(q_1,q_2) = 14 - (q_1+q_2)\)
- Profits are realized
- \(\pi_1(q_1,q_2) = (14 - [q_1 + q_2]) \times q_1 - 2q_1\)
- \(\pi_2(q_1,q_2) = (14 - [q_1 + q_2]) \times q_2 - 2q_2\)
How will firm 2 react to firm 1's quantity?
P(q_1,q_2) = 14 - (q_1+q_2)
c_2(q_2) = 2q_2
\pi_2(q_2) = P(q_1,q_2)q_2 - c_2(q_2)
= (14 - q_1 - q_2)q_2 - 2q_2
= 14q_2 - q_1q_2 - q_2^2 - 2q_2
\pi'_1(q_2) = 14-q_1 - 2q_2 - 2 = 0
q_2^*(q_1) = 6-\frac{1}{2}q_1
\text{total revenue}
\text{total cost}
\text{marginal revenue}
\text{marginal cost}
2
P
P(q_2|q_1) = 14-q_1 - q_2
MR(Q) = 14-q_1 - 2q_2
MC(q_2) = 2
6-\frac{1}{2}q_1
14-q_1
q_2
"Firm 2's Residual Demand Curve"
Firm 2's "reaction function"
Today's Agenda
Part 1: Simultaneous Move (Cournot)
Part 2: Infinitely Repeated Cournot
(cartels and collusion)
Each firm chooses its quantity
simultaneously and independently
Each firm "best responds" to what it believes the other firm will do
In Cournot equilibrium, each firm's beliefs are correct.
Firms are engaged in an ongoing relationship (produce every period)
If they collude by producing less than in Cournot equilibrium, they can raise their joint profits
Can cartel behavior be sustained even if each firm has an incentive to produce just a bit more...?
Cournot Duopoly
- Same setup as last time:
- two firms each choose their own quantity
- market price is determined by the total quantity produced
- Difference: timing
- before, firm 1 moved first; firm 2 observed \(q_1\) and chose \(q_2\).
- now: each firm chooses simultaneously and independently,
based on their belief about what the other firm will do - "best response function" says what the firm should do for each possible belief
- In Cournot equilibrium, each firm's belief about what the other firm does is correct.
- neither firm would want to change their output choice
once they learned what the other firm did
- neither firm would want to change their output choice
P(q_1,q_2) = 14 - (q_1+q_2)
c_2(q_2) = 2q_2
\pi_2(q_2|q_1) = P(q_1,q_2)q_2 - c_2(q_2)
= (14 - q_1 - q_2)q_2 - 2q_2
\pi'_2(q_2|q_1) = 12-q_1 - 2q_2 = 0
Before: how does firm 2 react if it observes firm 1 produce \(q_1\) units of output?
= 12 - q_1q_2 - q_2^2
2q_2 = 12 - q_1
q_2^*(q_1) = 6 - {1 \over 2}q_1
Firm 2's
reaction function
\pi_2(q_2|\hat q_1) = P(\hat q_1,q_2)q_2 - c_2(q_2)
= (14 - \hat q_1 - q_2)q_2 - 2q_2
\pi'_2(q_2|\hat q_1) = 12 - \hat q_1 - 2q_2 = 0
Now: what should firm 2 choose if it believes firm 1 will produce \(\hat q_1\)?
= 12 - \hat q_1q_2 - q_2^2
2q_2 = 12 - \hat q_1
q_2^*(\hat q_1) = 6 - {1 \over 2}\hat q_1
Firm 2's
best response function
P(q_1,q_2) = 14 - (q_1+q_2)
c_1(q_1) = 2q_1
\pi_1(q_1|r_2(q_1)) = P(q_1,r_2(q_1))q_1 - c_1(q_1)
= (14 - q_1 - [6 - {1 \over 2}q_1])q_1 - 2q_1
\pi'_1(q_1|r_2(q_1) = 6 - q_1
Before: what should firm 1 choose if it knows that \(q_2 = r_2(q_1) = 6 - {1 \over 2}q_1\)?
= 6 - {1 \over 2}q_1^2
q_1^* = 6
Optimal first move
\pi_1(q_1|\hat q_2) = P(q_1,\hat q_2)q_1 - c_1(q_1)
= (14 - q_1 - \hat q_2)q_1 - 2q_1
\pi'_1(q_2|\hat q_1) = 12 - \hat q_2 - 2q_1 = 0
Now: what should firm 1 choose if it believes firm 2 will produce \(\hat q_2\)?
= 12 - q_1\hat q_2 - q_1^2
2q_1 = 12 - \hat q_2
q_1^*(\hat q_2) = 6 - {1 \over 2}\hat q_2
Best response function
P(q_1,q_2) = 14 - (q_1+q_2)
c_1(q_1) = 2q_1
Stackelberg Model:
Firm 1 chooses first,
firm 2 observes \(q_1\) and chooses \(q_2\)
q_1^* = 6
Firm 1's optimal move
Cournot Model:
Both firms choose simultaneously and independently
q_1^*(\hat q_2) = 6 - {1 \over 2}\hat q_2
Firm 1's
best response function
c_2(q_2) = 2q_2
q_2^*(q_1) = 6 - {1 \over 2}q_1
Firm 2's
reaction function
q_2^*(\hat q_1) = 6 - {1 \over 2}\hat q_1
Firm 2's
best response function
Firm 1 makes its choice knowing firm 2 will observe and react to it.
Each firm makes its choice based on its beliefs about what the other firm will do.
(fundamentally asymmetric)
(symmetric)
Cournot Model:
Both firms choose simultaneously and independently
q_1^*(\hat q_2) = 6 - {1 \over 2}\hat q_2
Firm 1's
best response function
q_2^*(\hat q_1) = 6 - {1 \over 2}\hat q_1
Firm 2's
best response function
In equilibrium, each firm is
correct in its beliefs (so \(q_1 = \hat q_1\) and \(q_2 = \hat q_2\) ),
so each firm's quantity is a best response to the other firm's quantity.
q_1
q_2
q_1^*(\hat q_2) = 6 - {1 \over 2}\hat q_2
q_2^*(\hat q_1) = 6 - {1 \over 2}\hat q_1
q_1
q_2
q_1^*(\hat q_2) = 6 - {1 \over 2}\hat q_2
q_2^*(\hat q_1) = 6 - {1 \over 2}\hat q_1
Why is this different from Stackelberg?
In Stackelberg, firm 1 produced 6;
firm 2 observed this and produced 3.
If firm 1 believed firm 2 was going to produce 3 (and not observe firm 1's choice, so firm 1 can choose whatever it wants without consequence), what should firm 1 choose?
If firm 1 chose 4.5, what would firm 2 choose?
q_1^*(3) = 6 - {1 \over 2} \times 3 = 4.5
q_2^*(4.5) = 6 - {1 \over 2} \times 4.5 = 3.75
and on and on...
q_1
q_2
q_1^*(\hat q_2) = 6 - {1 \over 2}\hat q_2
q_2^*(\hat q_1) = 6 - {1 \over 2}\hat q_1
Another way of thinking about this:
if everyone knows everything about this model (and everyone knows that everyone knows everything about this model), what do each of the firms know about the other firm's beliefs?
Each firm knows the other
will never produce more than 6.
Because \(6 - {1 \over 2}6 = 3\),
this means each firm knows the other
will never produce less than 3.
Because \(6 - {1 \over 2}3 = 4.5\),
this means each firm knows the other
will never produce more than 4.5.
The only set of quantities that survives this is (4,4).
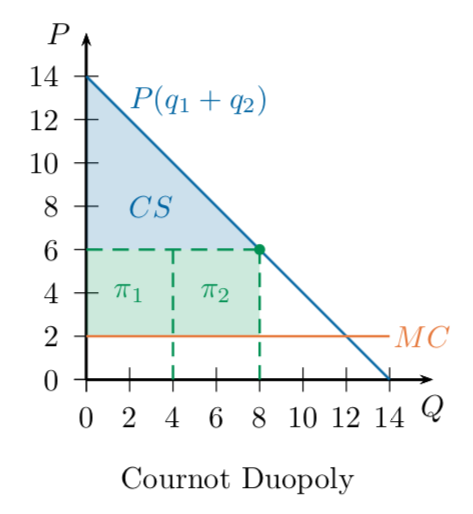
Profits in Cournot Equilibrium
Each firm is producing 4 units, so the market price is \(14 - 4 - 4 = 6\).
Each unit costs $2, so each firm is making
$4 of profit on 4 units = $16.
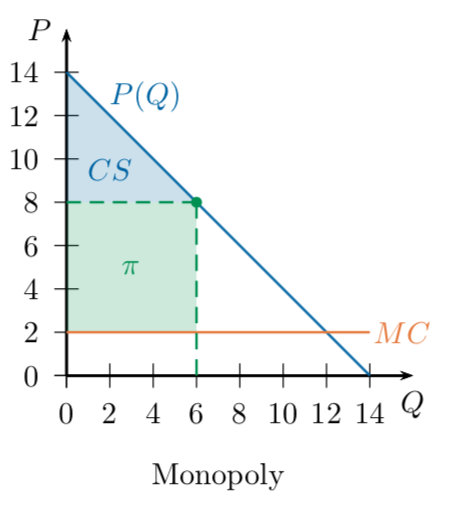
Remember our monopoly: it produced 6 units,
sold them at a price of 8, and earned a total profit of 36.
If each of these two firms produced 3 units, they could earn 18...
so why don't they?
Collusion
Repeated Games
- Analyze ongoing relationships
- Strategies are based on the history of all actions taken over the course of the relationship
- Agents can make promises or threats about how they will behave in the future
- Model as an "infinitely repeated game"
Evaluating Infinite Payoffs
V(\pi_0,\pi_1,\pi_2, \cdots) = \pi_0 + {\pi_1 \over 1 + r} + {\pi_2 \over (1 + r)^2} + \cdots
V(x,x,x, \cdots) = x + {x \over 1 + r} + {x \over (1 + r)^2} + \cdots
The present value of a stream of payoffs
(\(\pi_0\) now, \(\pi_1\) in the next period, \(\pi_2\) two periods from now, etc)
may be given by the sum
The present value of a stream of payoffs of \(x\) in every period is
x + {x \over r}
Value of getting payoff \(x\) forever, starting now:
Value of getting payoff \(z\) forever, starting next period:
Value of getting payoff \(y\) now and then payoff \(z\) forever after:
{z \over r}
y + {z \over r}
Monopoly: produces 6, profit of 36
Cournot equilibrium: each firm produces 4, receives profit of 16
Possible collusion: each firm produces 3, receives profit of 18
Best possible deviation: if the other firm produces 3,
produce 4.5, receive payoff of 20.25.
Sustaining Collusion
Should you deviate?
Suppose the other player is playing the grim trigger strategy:
"I will collude and play 3 as long as you collude and play 3.
If anyone has ever defected and not played 3, I will play the Cournot quantity of 4 forever."
Payoff from Colluding
Payoff from most profitable defection
Assume the other player is playing the grim trigger strategy:
"I will collude and play 3 as long as you collude and play 3.
If anyone has ever defected and not played 3, I will play the Cournot quantity of 4 forever."
Main Takeaway
- Cooperative (collusive) behavior can be sustained if agents are involved in an ongoing relationship and can make promises/threats about the future
- Their success depends on how much each agent values future payoffs.
- If you value the future a great deal, you're willing to go along with the relationship.
- If you're impatient and want to make a quick buck, you'll stab them in the back.
Section This Week
- Look at similar models in which firms choose price, not quantity
- Hotelling: firms are geographically separated; consumers care both about price and how close they are to the firm
- Bertrand with differentiated products: firms sell "weak substitutes" for one another; the higher your competitor's price is, the greater the demand for your product
Econ 51 | Fall 2022 | 8 | Oligopoly II
By Chris Makler
