Trading from an Endowment
Christopher Makler
Stanford University Department of Economics
Econ 51: Lecture 2
Today's Agenda
Part 1: Exchange Optimization
Part 2: Comparative Statics
Unit overview
The endowment budget line
Optimal choice with a constant price
Different prices for buying and selling
Optimization at general prices
Gross demand and net demand
Net demand and net supply
Application: labor supply
(as we have time; continued in section)
Econ 50
Consumer starts with money,
can buy a bundle of goods.
Econ 51
Consumer starts with a bundle,
can trade one good for another
Straight trade/barter
Sell some of one good for money,
use the money to buy the other good
Applications
Labor supply
"Good 1" = time
"Good 2" = money
Working: selling time for money
Intertemporal Choice
"Good 1" = money in the present
"Good 2" = money in the future
Saving: selling current money to
get more money in the future
Borrowing: selling future money to get more money in the present
"Goods" =
money in different
"states of the world"
Trading: betting, investing, insurance
Uncertainty and Risk
Trading from an Endowment
Good 1
Good 2
e_2
e_1
E
Note: lots of different notation for the endowment bundle!
Varian uses \(\omega\), some other people use \(x_1^E\)
x_2
x_1
X
Suppose you'd like to move from that endowment to some other bundle X
You start out with some endowment E
This involves trading some of your good 1 to get some more good 2
\Delta x_1
\Delta x_2
\Delta x_1 = e_1 - x_1
\Delta x_2 = x_2 - e_2
Buying and Selling
Good 1
Good 2
e_2
e_1
E
x_2
x_1
X
If you can't find someone to trade good 1 for good 2 directly, you could sell some of your good 1 and use the money to buy good 2.
Suppose you sell \(\Delta x_1\) of good 1 at price \(p_1\). How much money would you get?
What is the amount of good 2 you could buy with the proceeds, \(\Delta x_2\), at price \(p_2\)?
p_1 \Delta x_1
p_2 \Delta x_1
\Delta x_1
\Delta x_2
\Delta x_1 = e_1 - x_1
\Delta x_2 = x_2 - e_2
=
p_1 (e_1 - x_1)
=
p_2 (x_2 - e_2)
Buying and Selling
Good 1
Good 2
e_2
e_1
E
x_2
x_1
X
\Delta x_1
\Delta x_2
\Delta x_1 = e_1 - x_1
\Delta x_2 = x_2 - e_2
p_1 (e_1 - x_1)
=
p_2 (x_2 - e_2)
The amount you spend must be the amount you get, so:
The amount you spend must be the amount you get, so:
p_2x_2 - p_2e_2 = p_1e_1 - p_1x_1
p_1x_1 + p_2x_2 = p_1e_1 +p_2e_2
"value of the endowment at market prices"
Endowment Budget Line
Good 1
Good 2
e_2
e_1
E
p_1x_1 + p_2x_2 = p_1e_1 +p_2e_2
If you sell all your good 1 for \(p_1\),
how much good 2 can you consume?
If you sell all your good 2 for \(p_2\),
how much good 1 can you consume?
Endowment Budget Line
p_1x_1+p_2x_2=p_1e_1+p_2e_2
Divide both sides by \(p_2\):
Divide both sides by \(p_1\):
If \(x_1 = 0\):
If \(x_2 = 0\):
The budget line only depends on the price ratio \(p_1/p_2\), not the individual prices.
pollev.com/chrismakler
Effect of a Change in Prices
What happens if the price of good 1 doubles?
What happens if both prices double?
Optimization
Optimization problem with money
Optimization problem with an endowment
\displaystyle{\max_{x_1,x_2}\ u(x_1,x_2)}
\text{s.t. }p_1x_1 + p_2x_2 = m
\displaystyle{\max_{x_1,x_2}\ u(x_1,x_2)}
\text{s.t. }p_1x_1 + p_2x_2 = p_1e_1+p_2e_2
Procedure is exactly the same - we just have a different equation for the budget constraint.
pollev.com/chrismakler
Optimization: Income vs. Endowment
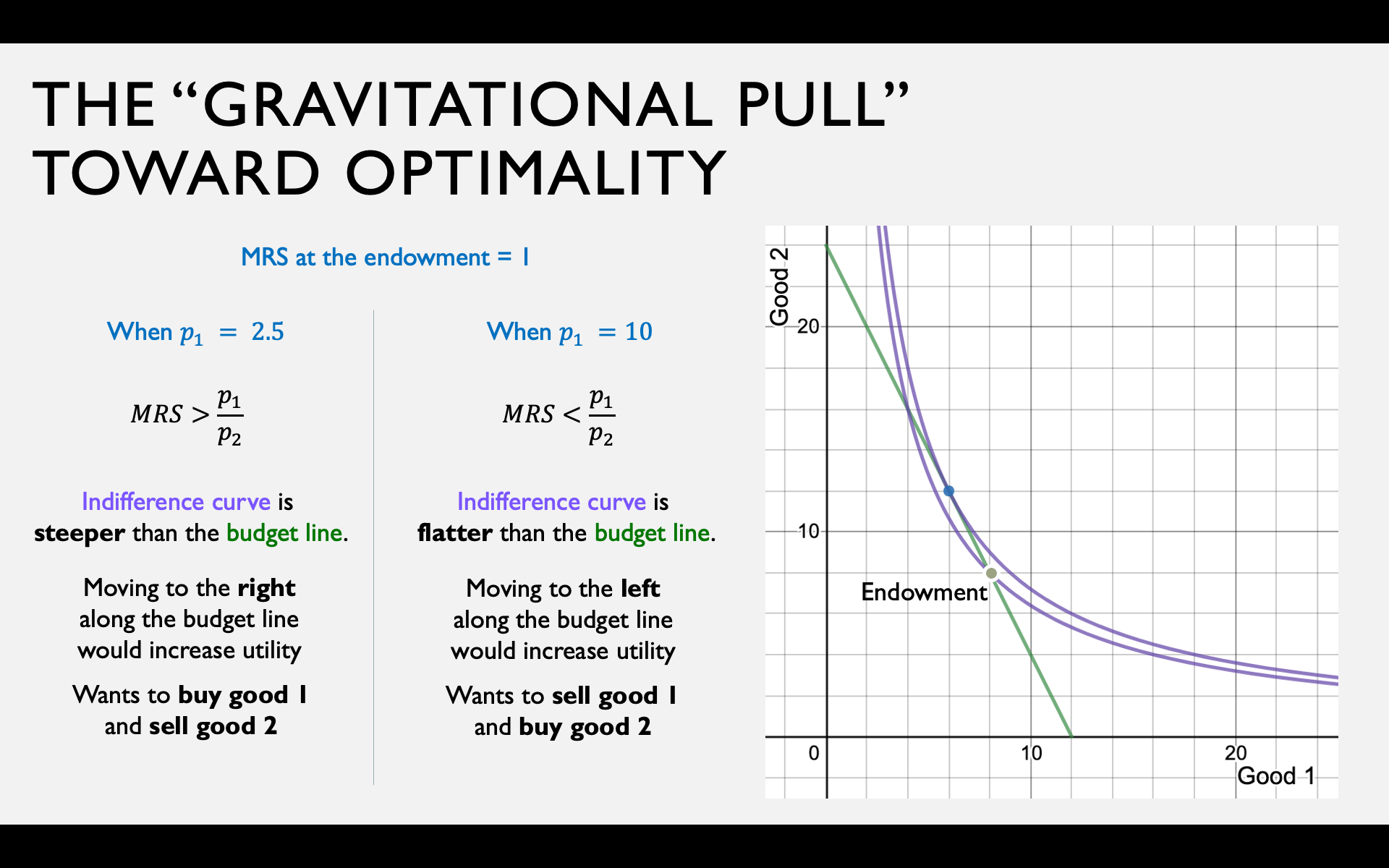
Recall: The “Gravitational Pull" Argument
MRS > {p_1 \over p_2}
MRS < {p_1 \over p_2}
Indifference curve is steeper
than the budget constraint
Can increase utility by
moving to the right
along the budget constraint
Indifference curve is flatter
than the budget constraint
Can increase utility by
moving to the left
along the budget constraint
Good 1
Good 2
pollev.com/chrismakler
Different Prices for Buying and Selling
Tickets
Money
If you sell all your tickets,
how much money will you have?
If you spend all your money on additional tickets, how many tickets will you have?
Suppose you have 40 tickets and $1200; you can sell tickets for $25 each,
or buy additional tickets for $60 each.
Part II: Comparative Statics
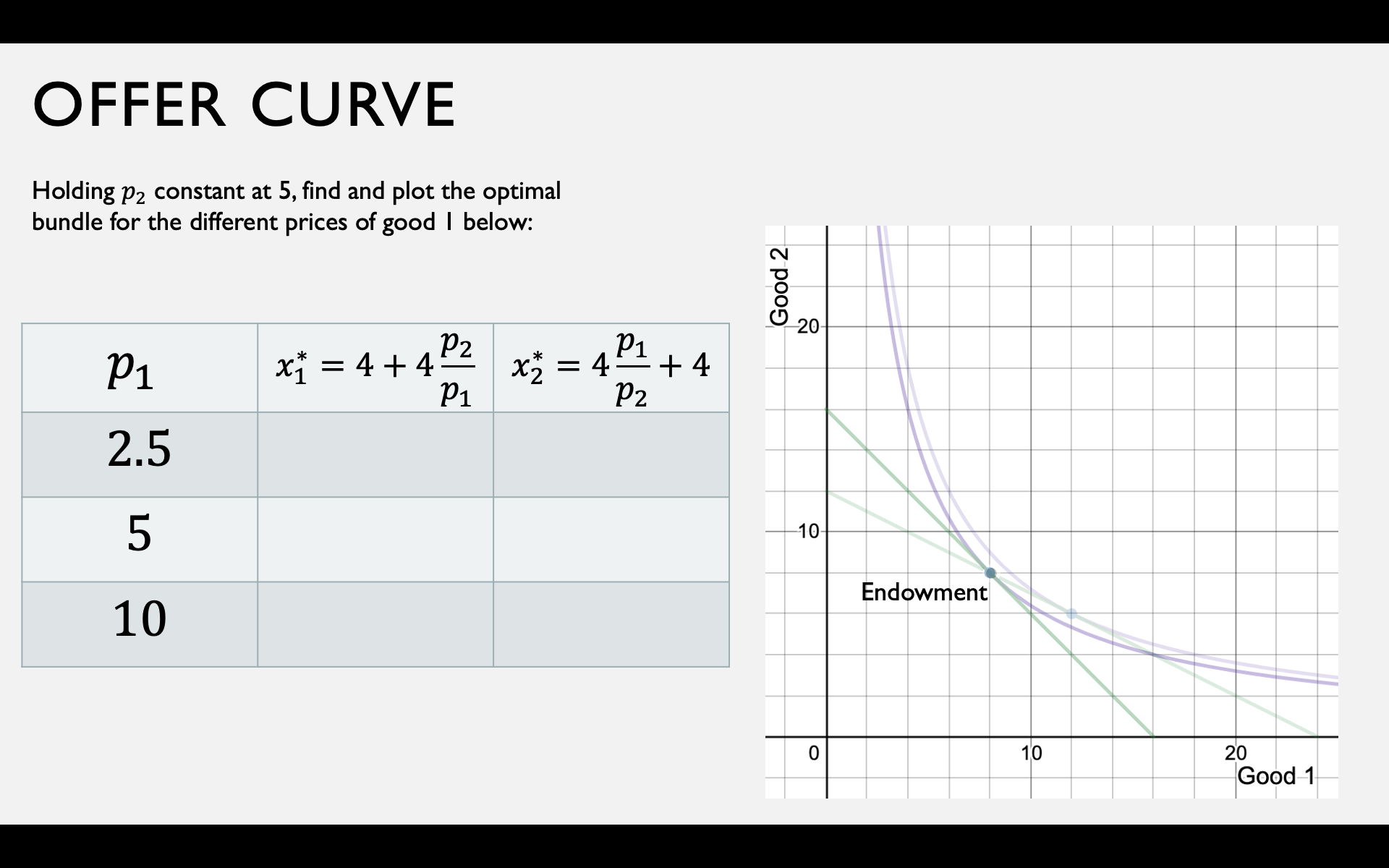
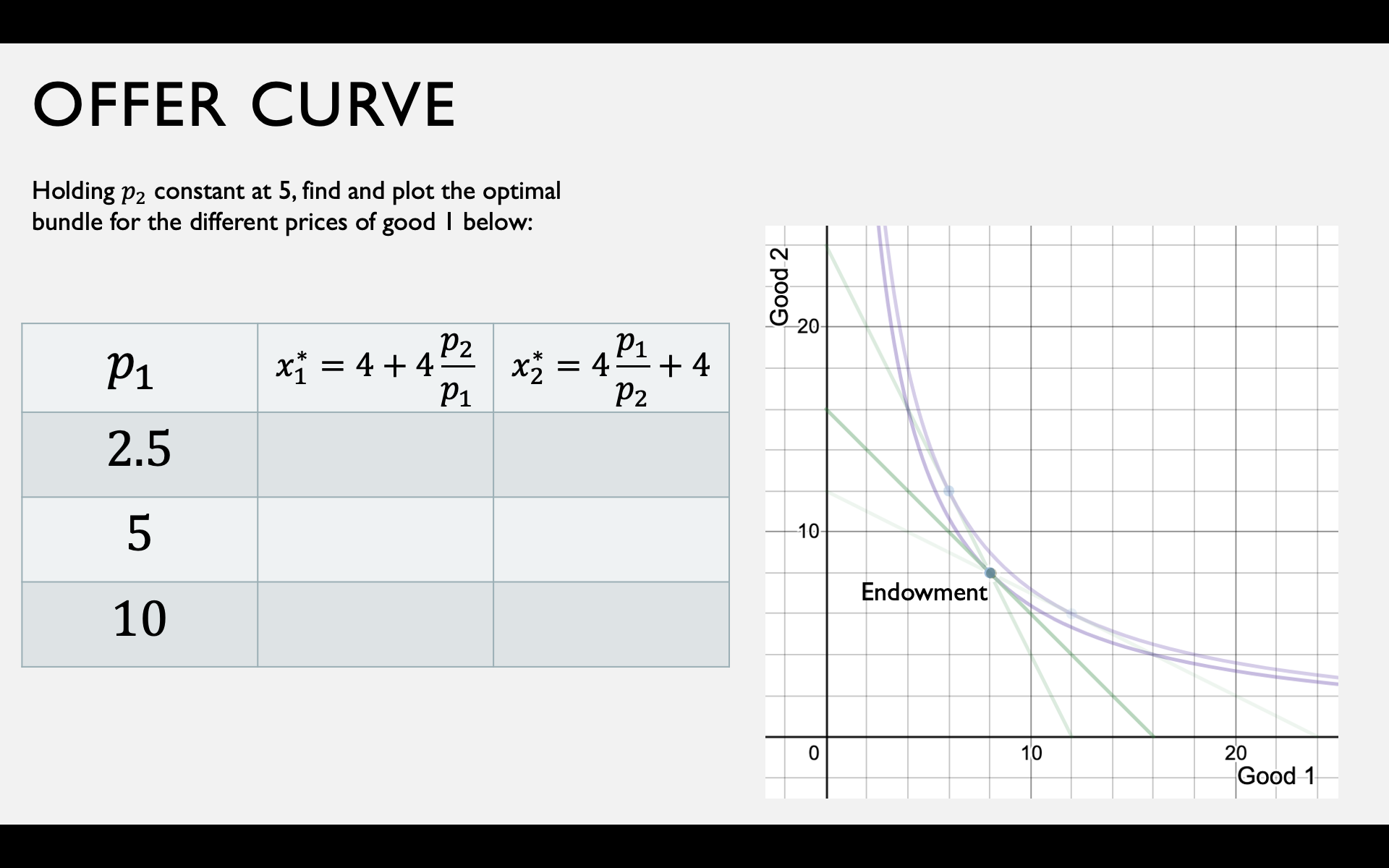
Gross Demands and Net Demands
The total quantity of a good
you want to consume (i.e. end up with)
at different prices.
Gross Demand
The transaction you want to engage in
(the amount you want to buy or sell)
at different prices.
Net Demand
x_1^*(p_1,p_2,e_1,e_2)
x_1^*(p_1,p_2,e_1,e_2) - e_1
\text{Net demand = }x_1^* - e_1
Is this positive or negative?
Positive: you are a net demander of good 1.
Negative: you are a net supplier of good 1.
d_1(p_1 | p_2) = \begin{cases} 0 & \text{ if } x_1^\star \le e_1\\x_1^\star - e_1 & \text{ if } x_1^\star \ge e_1\end{cases}
s_1(p_1 | p_2) = \begin{cases}e_1 - x_1^\star & \text{ if } x_1^\star \le e_1 \\ 0 & \text{ if } x_1^\star \ge e_1\end{cases}
Application 1:
Labor Supply
Leisure-Consumption Tradeoff
Leisure (R)
Consumption (C)
24
24 - L
M
M + \Delta C
You trade \(L\) hours of labor for some amount of consumption, \(\Delta C\).
You start with 24 hours of leisure and \(M\) dollars.
L
\Delta C
You end up consuming \(R = 24 - L\) hours of leisure,
and \(C = M + \Delta C\) dollars worth of consumption.
R
Selling Labor at a Constant Wage
Leisure (R)
Consumption (C)
24
24 - L
M
M + wL
You sell \(L\) hours of labor at wage rate \(w\).
You start with 24 hours of leisure and \(M\) dollars.
You earn \(\Delta C = wL\) dollars in addition to the \(M\) you had.
L
wL
M + 24w
C = M + wL
C = M + w(24 - R)
...and you consume \(R = 24 - L\) hours of leisure.
wR + C = 24w + M
Budget Line Equation
Leisure (R)
Consumption (C)
24
M
M + 24w
wR + C = 24w + M
p_1x_1 + p_2x_2 = p_1e_1 + p_2e_2
x_1: R
x_2: C
p_1: w
p_2: 1
e_1: 24
e_2: M
This is just an endowment budget line
Optimal Supply of Labor
Preferences are over the two "good" things: leisure and consumption
u(R,C)
wR + C = 24w + M
We've just derived the budget constraint in terms of leisure and consumption as well:
Maximize utility as usual, with one caveat:
you can only sell your leisure time, not buy it.
When will labor supply be zero?
Remember: you only want to sell good 1 (in this case, your time) if
MRS(e_1,e_2)<{p_1 \over p_2}
Most Important Takeaways
The endowment budget line depends only on the price ratio, not on individual prices.
Whether you're a net demander or supplier depends on the relationship between the price ratio and the MRS at the endowment.
Logistics
There is section this week!
Office hours have been posted.
Mine will feature a puppy.
First homework is due Sunday night
(no-penalty deadline is 8am Monday,
no homeworks accepted after that)
Econ 51 | 2 | Trading from an Endowment
By Chris Makler
Econ 51 | 2 | Trading from an Endowment
Spring 22 Econ 51 Lecture 2
