Mechanism Design and the Principal-Agent Model
Christopher Makler
Stanford University Department of Economics
Econ 51: Lecture 16
Both of these are models of asymmetric information: an uninformed party is trying to extract behavior or information from an informed party.
Today:
The Principal-Agent Model
Thursday:
Price Discrimination
- Buyers differ as to their valuation of quality: some value it a lot, others not so much
- A seller cannot observe how much the buyer values quality
- Offers a menu of options: a "budget" product at a low price point, and a "premium" product at a higher price point
- Goal: have buyers sort themselves
- A "principal" wants an "agent" to do something for them
- The principal cannot observe how much effort the agent puts forward, but can observe if the agent is successful
- Offers a wage contract with two values: one if the agent fails, the other if they succeed
- Goal: encourage effort
Also: market for lemons
Mechanism Design
Game
Players
Strategies
Payoffs
Mechanism
Players with Hidden Information
Actions
Outcomes
Given this game,
what outcome do we predict will happen?
Given a desired outcome,
what game can we design to achieve it?
"Reverse Game Theory"
The designer is interested in the outcome
but lacks complete information
Selling train tickets to people with different valuations
Auctioning off a painting to people with different (private) valuations
Splitting rent / choosing rooms in an apartment
Hiring an employee/contractor whose effort you can't observe
Selling a car whose type (quality) isn't observable
Fundamental Questions
If people have hidden information,
(there's an adverse selection problem)
what mechanism can a designer establish
to get them to reveal that information?
If people can take hidden actions,
(there's a moral hazard problem)
what mechanism can a designer establish
to get them to choose the action the designer wants them to take?
Principal: Someone who needs someone else to do something
Agent: The person who needs to do the thing
CEO / sales rep
Professor / student
Landowner / farmer
The principal's payoff depends on the actions of the agent
Can they incentivize the agent to do what they want?
Principal-Agent Model
I want to hire you to do a project.
- If you succeed, it’s worth \(Q^H = 400\) to me
- If you fail, it’s worth \(Q^L = 100\) to me
You choose whether to exert effort \((e)\):
- If you exert effort \((e = 1)\), you succeed with probability \(p = {2 \over 3}\)
- If you shirk \((e = 0)\), you succeed with probability \(p = {1 \over 3}\)
- Exerting effort costs \(c(e) = e\); that is, exerting effort costs \(c = 1\), while shirking costs \(c = 0\).
I can choose a wage stucture \(w\). Payoffs:
- Me (the principal) is Risk-Neutral: \(u_P(Q,w) = Q - w\)
- You (the agent) are Risk-Averse: \(u_A(w,e) = \sqrt{w} - c(e)\)
- If you reject the deal, you get a payoff of \(\underline u = 10\)
Note: "Nature" chooses whether the agent succeeds or fails; but the action the agent takes affects the probabilities
- Success: worth \(Q^H = 400\) to principal
- Failure: worth \(Q^L = 100\) to principal
- Payoff to principal: \(Q - w\)
- Effort: costs \(c=1\), succeed with probability \(p = {2 \over 3}\)
- Shirk: costs \(c=0\), succeed with probability \(p = {1 \over 3}\)
- Payoff to agent: \(\sqrt{w} - c\); outside option \(\underline u = 10\)
Benchmark Model: Contractible Effort
Suppose I can observe your effort.
If I write a contract to require shirking:
I can write a contract that specifies and effort level and a wage if you exert that effort.
If I write a contract to require effort:
\sqrt{w} - c(0) \ge \underline u
\sqrt{w} - c(0) \ge \underline u
\sqrt{w} - 0 \ge 10
w \ge 100
\sqrt{w} - 1 \ge 10
w \ge 121
- Success: worth \(Q^H = 400\) to principal
- Failure: worth \(Q^L = 100\) to principal
- Payoff to principal: \(Q - w\)
- Effort: costs \(c=1\), succeed with probability \(p = {2 \over 3}\)
- Shirk: costs \(c=0\), succeed with probability \(p = {1 \over 3}\)
- Payoff to agent: \(\sqrt{w} - c\); outside option \(\underline u = 10\)
Benchmark Model: Contractible Effort
Suppose I can observe your effort.
If I write a contract to require shirking:
I can write a contract that specifies and effort level and a wage if you exert that effort.
If I write a contract to require effort:
w = 100
w = 121
NOTE: WE WILL ASSUME THAT IF THE AGENT IS INDIFFERENT, THEY'LL CHOOSE WHAT THE PRINCIPAL WANTS
Expected value of project:
{1 \over 3} \times 400 + {2 \over 3} \times 100 = 200
Expected payoff: 200 - 100 = 100
Expected value of project:
{2 \over 3} \times 400 + {1 \over 3} \times 100 = 300
Expected payoff: 300 - 121 = 179
- Success: worth \(Q^H = 400\) to principal
- Failure: worth \(Q^L = 100\) to principal
- Payoff to principal: \(Q - w\)
- Effort: costs \(c=1\), succeed with probability \(p = {2 \over 3}\)
- Shirk: costs \(c=0\), succeed with probability \(p = {1 \over 3}\)
- Payoff to agent: \(\sqrt{w} - c\); outside option \(\underline u = 10\)
Unobservable Effort
Now suppose I cannot observe your effort; I can only observe whether or not you succeed.
I can write a contract that specifies a wage level if you succeed \((w_H)\), and one if you fail \((w_L)\).
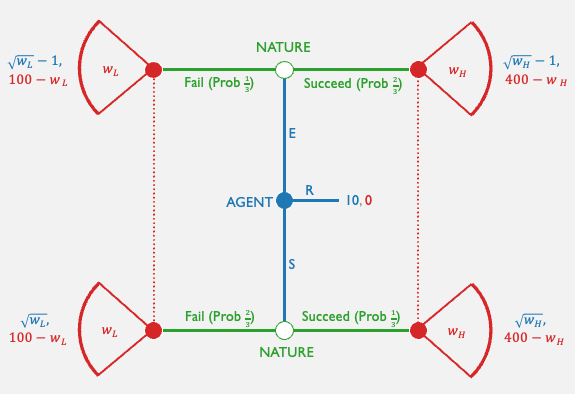
- Success: worth \(Q^H = 400\) to principal
- Failure: worth \(Q^L = 100\) to principal
- Payoff to principal: \(Q - w\)
- Effort: costs \(c=1\), succeed with probability \(p = {2 \over 3}\)
- Shirk: costs \(c=0\), succeed with probability \(p = {1 \over 3}\)
- Payoff to agent: \(\sqrt{w} - c\); outside option \(\underline u = 10\)
If you shirk:
If you exert effort:
u_A(S) = {1 \over 3}\sqrt{w_H} + {2 \over 3}\sqrt{w_L}
u_P(S) = {1 \over 3}(400 - w_H) + {2 \over 3}(100 - w_L)
u_A(E) = {2 \over 3}\sqrt{w_H} + {1 \over 3}\sqrt{w_L} - 1
u_P(E) = {2 \over 3}(400 - w_H) + {1 \over 3}(100 - w_L)
If you reject the contract: \(u_A(R) = 10, u_P(R) = 0\)
INCENTIVE COMPATIBILITY CONSTRAINT
Exerting effort
should be better than not exerting effort
PARTICIPATION CONSTRAINT
Accepting the contract (and exerting effort)
should be better than rejecting the contract.
u_A(E) \ge u_A(S)
u_A(E) \ge u_A(R)
pollev.com/chrismakler
The incentive compatibility constraint is set so that...
If you shirk:
If you exert effort:
u_A(S) = {1 \over 3}\sqrt{w_H} + {2 \over 3}\sqrt{w_L}
u_A(E) = {2 \over 3}\sqrt{w_H} + {1 \over 3}\sqrt{w_L} - 1
If you reject the contract: \(u_A(R) = 10, u_P(R) = 0\)
INCENTIVE COMPATIBILITY CONSTRAINT
Exerting effort
should be better than not exerting effort
PARTICIPATION CONSTRAINT
Accepting the contract (and exerting effort)
should be better than rejecting the contract.
u_A(E) \ge u_A(S)
u_A(E) \ge u_A(R)
{2 \over 3}\sqrt{w_H} + {1 \over 3}\sqrt{w_L} - 1 \ge {1 \over 3}\sqrt{w_H} + {2 \over 3}\sqrt{w_L}
{2 \over 3}\sqrt{w_H} + {1 \over 3}\sqrt{w_L} - 1 \ge 10
{1 \over 3}\sqrt{w_H} - {1 \over 3}\sqrt{w_L} \ge 1
\sqrt{w_H} \ge 3 + \sqrt{w_L}
{2 \over 3}(3 + \sqrt{w_L}) + {1 \over 3}\sqrt{w_L} - 1 \ge 10
\sqrt{w_L} \ge 9
w_L \ge 81
\ge 12
w_H \ge 144
- Success: worth \(Q^H = 400\) to principal
- Failure: worth \(Q^L = 100\) to principal
- Payoff to principal: \(Q - w\)
- Effort: costs \(c=1\), succeed with probability \(p = {2 \over 3}\)
- Shirk: costs \(c=0\), succeed with probability \(p = {1 \over 3}\)
- Payoff to agent: \(\sqrt{w} - c\); outside option \(\underline u = 10\)
If you shirk:
If you exert effort:
u_A(S) = {1 \over 3}\sqrt{w_H} + {2 \over 3}\sqrt{w_L}
u_P(S) = {1 \over 3}(400 - w_H) + {2 \over 3}(100 - w_L)
u_A(E) = {2 \over 3}\sqrt{w_H} + {1 \over 3}\sqrt{w_L} - 1
u_P(E) = {2 \over 3}(400 - w_H) + {1 \over 3}(100 - w_L)
Potential contract: \(w_L = 81\), \(w_H = 144\)
What's the payoff to the principal?
u_P(E) = {2 \over 3}(400 - 144) + {1 \over 3}(100 - 81)
= {2 \over 3} \times 256 + {1 \over 3} \times 19
= 177
This is worse than the 179 when they could contract under perfect information;
but better than just accepting shirking and getting a payoff of 100.
Where does risk aversion come in?
- In this example: principal is risk neutral, agent is risk averse
- Offering a bonus encourages effort, but the agent doesn't like it because they don't like risk
- If the agent is extremely risk averse, the only possible contract would be a fixed salary (with no incentive to exert effort)
- If the agent approaches risk neutrality, the bonus can be bigger and bigger. In the extreme, the principal could offer the entire 300 ( = 400 - 100) as a bonus, effectively having the agent bear all the risk and all the reward for success.
Adverse Selection
The Market For Lemons
(Akerlof 1970)
There are two types of used cars: "lemons" and "plums"
- Lemons (🍋) are worth $1000 to a seller and $1200 to a buyer
- Plums (🥭) are worth $2000 to a seller and $2400 to a buyer
If the quality of a car is observable to a buyer, which types of cars will sell?
If the quality is not observable to a buyer, and an equal number of each type of cars are on the market, what is the expected value to a buyer from buying a random car?
If that's the most buyers are willing to spend, which cars will be offered for sale?
🍋
🥭
$1800
🍋
There are two types of used cars: "lemons" and "plums"
- Lemons (🍋) are worth $1000 to a seller and $1200 to a buyer
- Plums (🥭) are worth $2000 to a seller and $2400 to a buyer
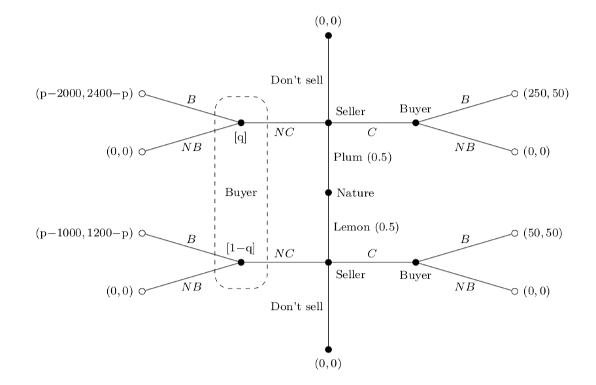
Suppose the seller could pay $100 to get their car quality certified (C).
Assume that if the car is certified, its quality is revealed and it is sold for $50 less than the buyer value.
If a car is not certified, its quality is still unknown.
🍋
🥭
(The seller can also choose not to sell)
There are two types of used cars: "lemons" and "plums"
- Lemons (🍋) are worth $1000 to a seller and $1200 to a buyer
- Plums (🥭) are worth $2000 to a seller and $2400 to a buyer
🍋
🥭
Separating PBE:
Sellers of plus get their cars certified.
Sellers of lemons do not.
Buyers of uncertified cars believe an uncertified car
is a lemon (q = 0)
and pay p = 1150.
(150, 50)
(-850, 1250)
Econ 51 | 16 | Moral Hazard and Adverse Selection
By Chris Makler
Econ 51 | 16 | Moral Hazard and Adverse Selection
How to design a mechanism to get someone to behave a certain way, or to reveal their true preferences
