Nash Equilibrium
To navigate: press "N" to move forward and "P" to move back.
To see an outline, press "ESC". Topics are arranged in columns.
Today's Agenda
Part 1: Discrete Strategies
Part 2: Continuous Strategies
Nash Equilibrium
Mixed-Strategy Nash Equilibrium
Baseline Case: Monopoly
Quantity Choice: Cournot
Location Choice: Median Voter Theorem
Nash Equilibrium
Definition: Nash Equilibrium
A strategy profile in which every player
is playing a best response to the strategies played by the other players.
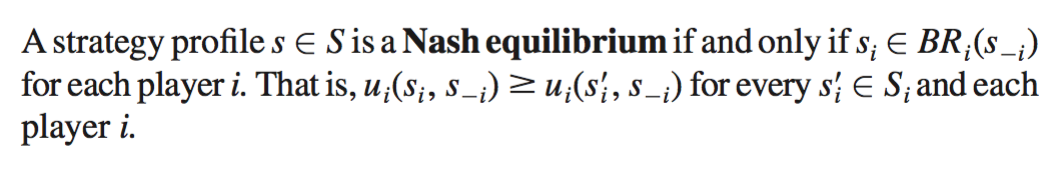
Wait a Second!
Chapter 6:
Chapter 9:
BR is a function of beliefs about strategies
BR is a function of strategies (not beliefs)
What happened in that sea of text between these two definitions?
We made the assumption that beliefs are accurate.
Recall: Strategic Uncertainty
When I didn't let the players talk,
both of them chose Hare.
What if I let them talk?
Possible rationales for strategic certainty:
- People play this game all the time, and reasonably expect
the other player to play according to the equilibrium. - The players have agreed on a strategy before the game is played;
as long as no one has an incentive to deviate, it's OK. - An outside mediator (society, the law) recommends a strategy profile
Example: Party or Not?
Players: Two friends, Veronica and Heather
Strategy Spaces: {"Party", "Stay In"}
Payoffs:
Both would rather do what the other is doing
Both would rather go to the party
Stay In
Party
Party
Stay In
Heather
Veronica
2
2
0
0
0
0
1
1
("Pareto Coordination" game)
Players: Two friends, Chris and Pat
Strategy Spaces: {"Opera", "Fight"}
Payoffs:
They each get no payoff if they don't go to the same place.
Chris gets a higher payoff if they both go to the opera
Pat gets a higher payoff if they both go to the prize fight
Fight
Opera
Opera
Fight
Pat
Chris
2
1
0
0
0
0
1
2
Example: Opera or Prize Fight
("Battle of the Sexes" game)
Third Strategic Tension:
Inefficient Coordination
Recall: Party or Not?
Players: Two friends, Veronica and Heather
Strategy Spaces: {"Party", "Stay In"}
Payoffs:
Both would rather do what the other is doing
Both would rather go to the party
Stay In
Party
Party
Stay In
Heather
Veronica
2
2
0
0
0
0
1
1
("Pareto Coordination" game)
Dvorak vs QWERTY
Players: Companies buying computer keyboards
Strategy Spaces: {"Dvorak", "QWERTY"}
Payoffs:
Both would rather do what the other is doing (so new workers can type)
Both would rather use Dvorak (workers more productive)
QWERTY
Dvorak
Dvorak
QWERTY
2
2
0
0
0
0
1
1
Mixed-Strategy Nash Equilibrium
Example: Matching Pennies (Zero-sum game)
Players: Two bettors, Ros and Guil
Strategy Spaces: {"Heads", "Tails"}
Payoffs:
If they're both the same, Ros wins
If they're different, Guil wins
Tails
Heads
Heads
Tails
Guil
Ros
1
-1
-1
1
-1
1
1
-1
There is no pure-strategy equilibrium.
Is there an equilibrium in mixed strategies?
If Guil plays H with probability \(q\), what is Ros's payoff to playing H? To playing T?
What is Ros's best response to Guil playing the mixed strategy \((q, 1-q)\)?
What, therefore, is Guil's best response to Ros playing the mixed strategy \((p, 1-p)\)?
What equilibrium exists in which both players are best responding to one another?
If a player is to play a mixed strategy, they must be indifferent between all the strategies to which they assign positive probability.
Key Insight
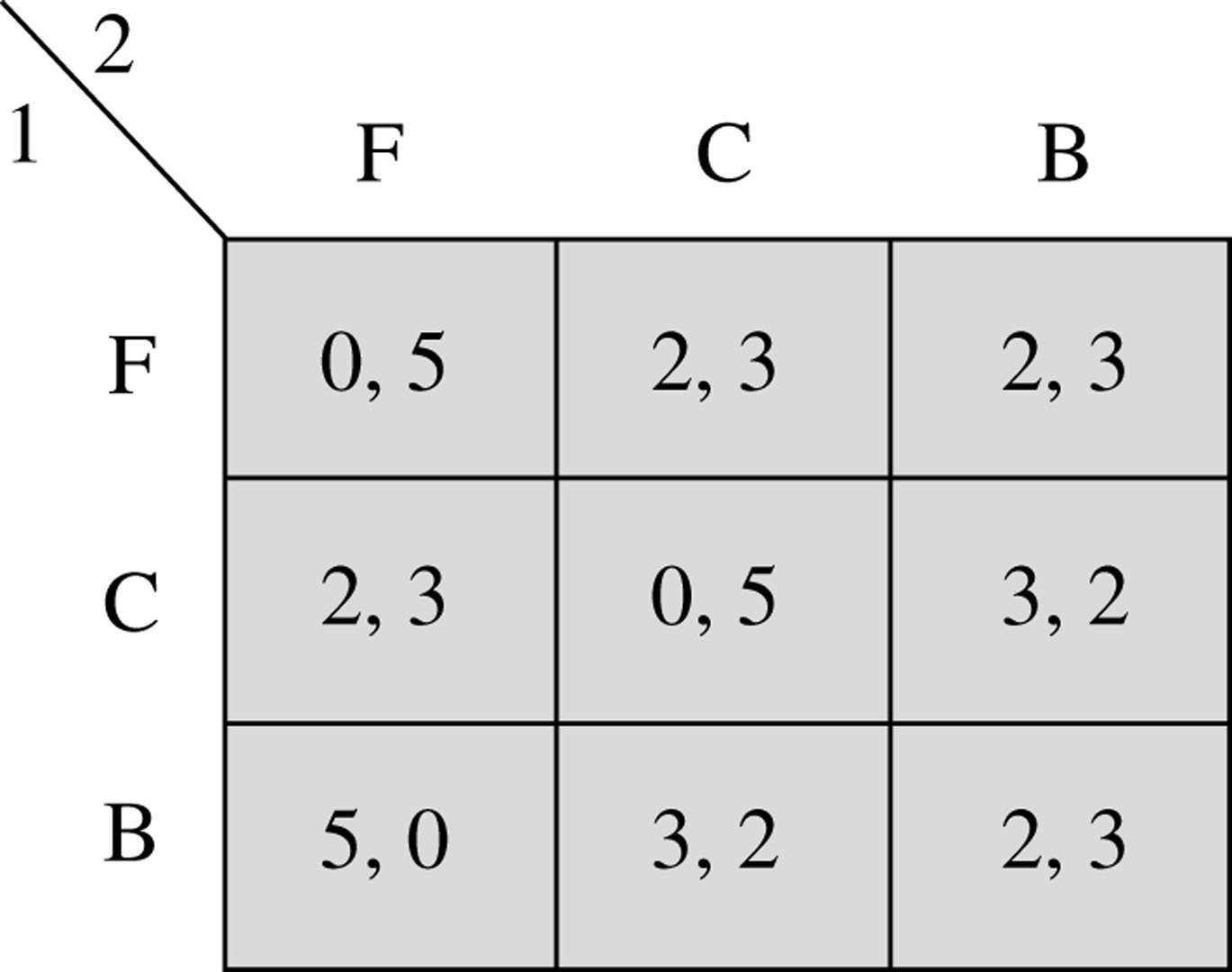
Tennis!
F = forehand
C = center
B = backhand
Server: player 1
Returner: player 2
Continuous Strategies
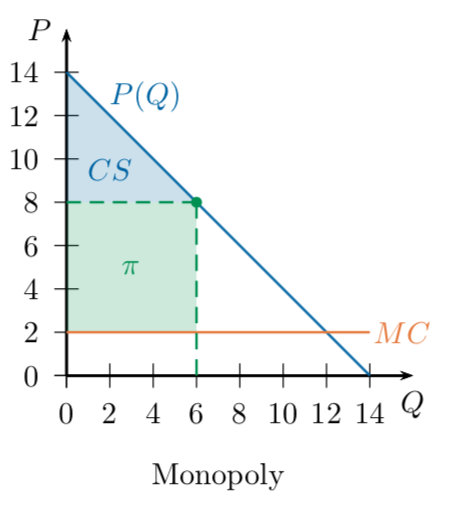
Baseline Case: Monopoly
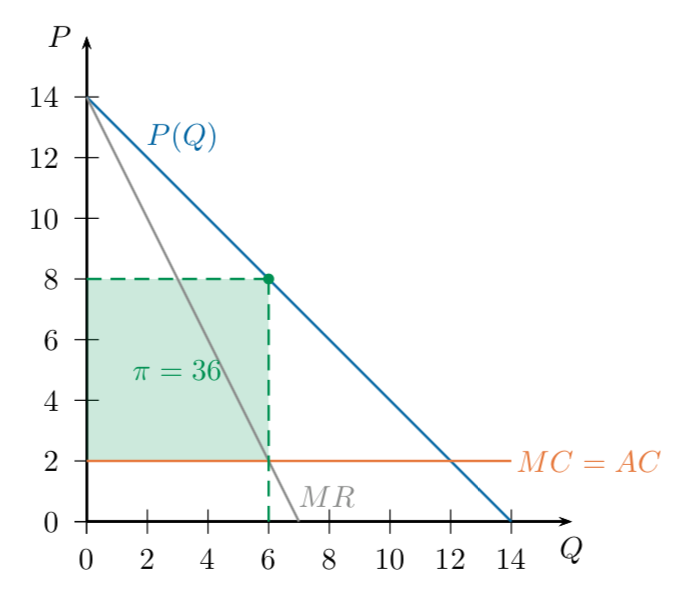
A single-price monopolist faces an inverse demand curve P(Q)
which determines the market price if it produces Q units of output.
The monopolist's profit-maximization problem is to choose Q to maximize:
\pi(Q) = P(Q)Q -c(Q)
Maximize by taking the derivative and setting equal to zero.
\text{total revenue}
\text{total cost}
P(Q) = 14 - Q
c(Q) = 2Q
\text{Market Demand:}
\text{Monopoly's Costs: }
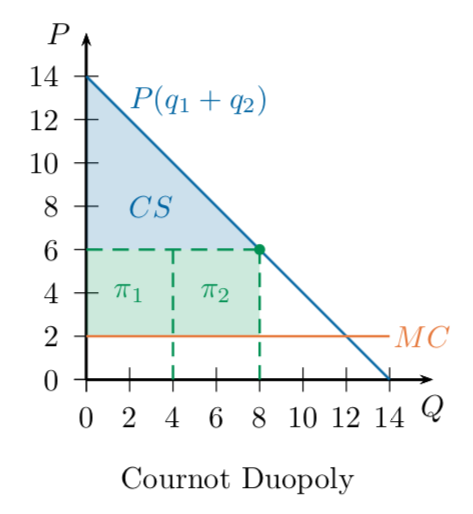
Quantity Choice: Cournot Duopoly
c_1(q_1) = 2q_1
c_2(q_2) = 2q_2
\text{Firm 1's Costs:}
\text{Firm 2's Costs:}
Cournot (Quantity) Duopoly
Players: Two firms, Firm 1 and Firm 2
Strategy Spaces: each firm chooses a level of output \(q_i\)
Outcome:
Market price is determined by total output produced:
Profit to each firm is
P(q_1,q_2)
\pi_i(q_i,q_{-i}) = P(q_i,q_{-i})q_i - c_i(q_i)
Payoffs:
P(Q) = 14 - Q
\text{Market Demand:}
Best-Response Functions
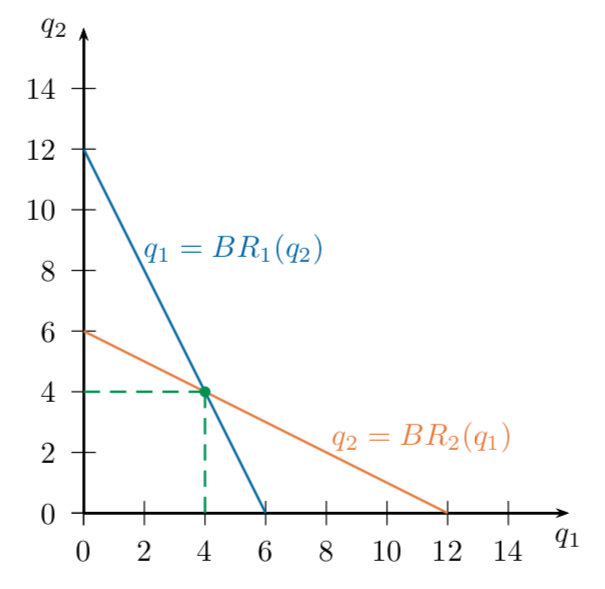
What is the Nash Equilibrium of this game?
P = 8, Q = 6
CS = 18
\pi = 36
P = 6, Q = 8
CS = 32
\pi_1 = \pi_2 = 16
P = 2, Q = 12
CS = 72
\sum \pi = 0
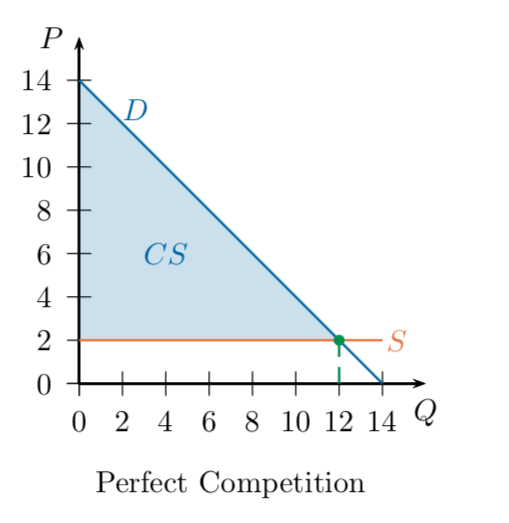
Econ 51 | 11 | Nash Equilibrium
By Chris Makler
Econ 51 | 11 | Nash Equilibrium
Nash equilibrium with pure and mixed strategies; Cournot and Hotelling models
