String
資訊讀書會的字串字串
雜湊(哈希)
唬爛(但他是好的
Hash
字典樹啦~
北市賽有考
trie
另一個字串匹配
似乎比較好寫?
Zalgorithm
好的字串匹配
Failure Function
KMP
跟Z很像
專門處理迴文
Manacher
複習一下
字串的語法小整理
什麼是字串
我是一條字串~
我也是喔
I am a string too.
就字元的陣列啦
一些字串的語法
#include<iostream>
#include<string>
using namespace std;
int main(){
string a;
cin >> a;
getline(cin, a);
int l=a.length();
a+="abc";
a[1]='e';
string b=a.substr(3, 5);
}字串匹配
什麼是字串匹配
在字串裡面找字串
有點像command+f (ctrl+f)
abaabaaababb
欲找aab
字串匹配
abaabaaababb
方法#1
就直接兩個for迴圈開下去了啊
複雜度O(N^2)
int main(){
string a, b;
cin >> a >> b;
for(int i=0;i<=a.length()-b.length();i++){
bool find=1;
for(int j=0;j<b.length;j++){
if(a[i+j]!=b[j]) find=0;
}
if(find) cout << i << endl;
}
}好慢喔
其實可以跑更快
等一下會講O(N)
雜湊
什麼是雜湊
隨便湊一湊
把字串當數字在用
f(string)=int
雜湊Hash
阿字串這麼長怎麼變整數
---> 資料壓縮
把長度為\(N\)的字串當成是\(N\)位數
並以某數\(p\)進位,最後再模\(M\)
常用雜湊法
\(\left ( a_{0}\times p^{n-1}+a_{1}\times p^{n-2}+...+a_{n-1}\times p^{0} \right )\%M\)
大概長這樣兒
\(\left ( a_{0}\times p^{0}+a_{1}\times p^{1}+...+a_{n-1}\times p^{n-1} \right )\%M\)
當然也可以這樣
阿上面提到的\(p\)跟\(M\)
最好要是兩個質數
p要比字元個數還要大\((29, 257)\)
M就選個很大的質數\((10^9+7, 998244353 )\)
常用雜湊法
這時候要比對兩字串是否相同
就直接比較兩字串Hash出來的數字就好了
字串匹配
雜湊是好的要基於:
同一個字串只會Hash出一個數字
且我們相信不同的字串很難湊出同樣的數字
因為我們剛才的雜湊函數是多項式形式
可以對每個字串的前綴都記錄一次
這樣要取子字串時只要用前綴相減取區間和
但要注意得出來的雜湊值可能多乘過p的幾次
再把他除掉還原回來即可
字串匹配
扣的
#include <iostream>
#define ll long long
using namespace std;
const ll p=257, M=1e9+7;
ll shash[1000005 ], thash[1000005 ], pp=1, ans=0;
int main(){
string s, t;
cin >> s >> t;
ll n=s.length(), m=t.length();
shash[0]=thash[0]=0;
for(int i=1;i<=n;i++){
shash[i]=(shash[i-1]+pp*s[i-1])%M;
pp=(pp*p)%M;
}
pp=1;
for(int i=1;i<=m;i++){
thash[i]=(thash[i-1]+pp*t[i-1])%M;
pp=(pp*p)%M;
}
pp=1;
for(int i=0;i<=n-m;i++){
if((shash[i+m]-shash[i]+M)%M==thash[m]*pp%M) ans++;
pp=(pp*p)%M;
}
cout << ans << endl;
return 0;
}題目
字典樹
就是查字典
平常查英文字典的時候
我們會找第一個字母、第二個字母......
直到我們找到要找的字串
把每次找尋看成一條邊
---> 字典樹
字典樹trie
字典樹trie
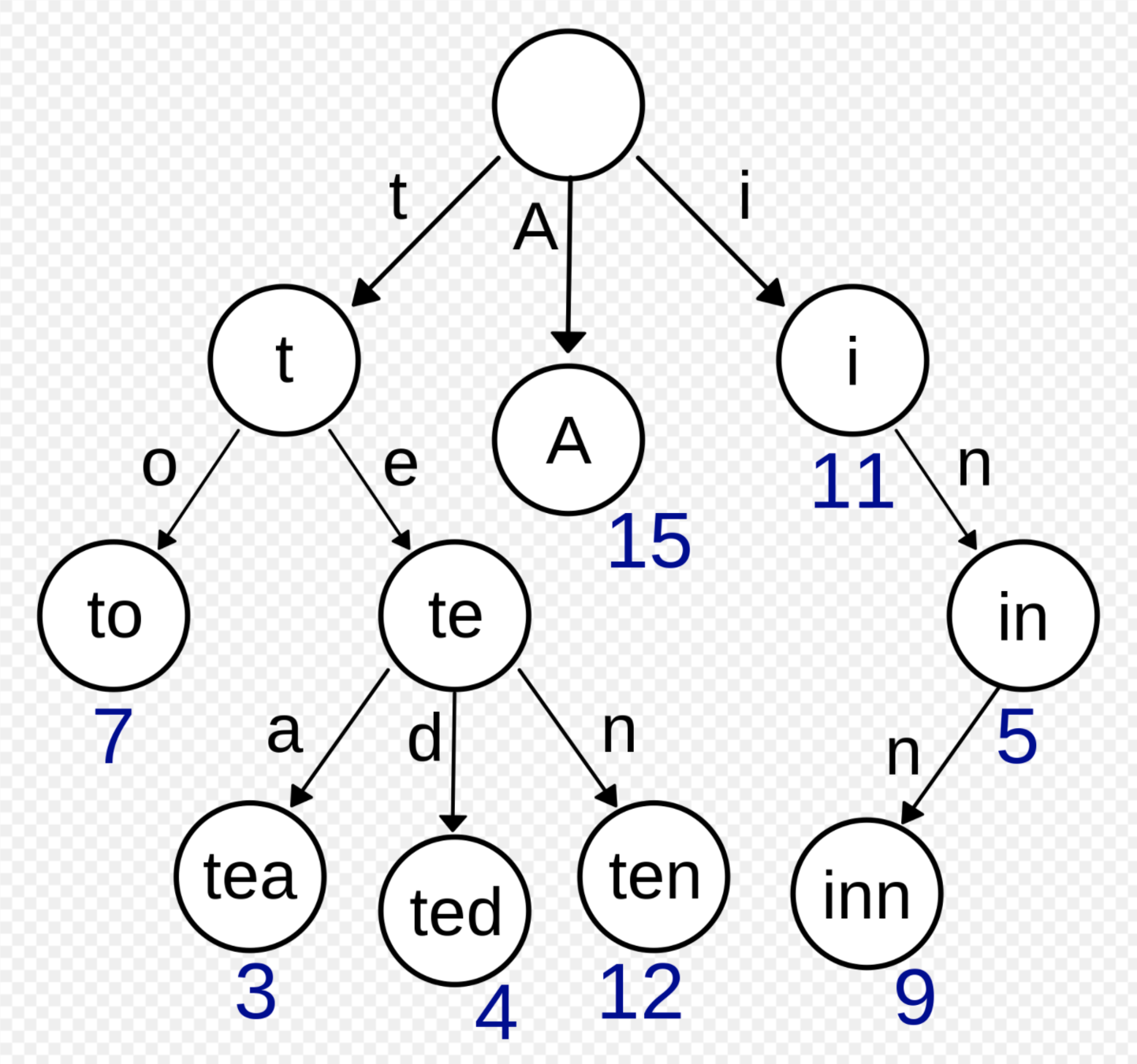
tea : 3
ted : 4
in : 5
to : 7
inn : 9
i : 11
ten : 12
A : 15
實作
就實作一棵樹出來
每個節點存他可以連到的節點(偽指標?
這部分可以用map或直接用陣列
用map多帶log,用陣列多吃空間
題目
KMP
Knuth Morris Pratt algorithm
KMP字串匹配演算法的精髓
定義如下:
\(\pi [k]=\underset{i=0,1,...,k}{max}i\)
\(i:s[0\sim i-1]=s[k-(i-1) \sim k]\)
Failure function
剛才的東西用文字說明就是:
k-前綴字串的「次長共同前後綴」
次長共同前後綴
aabaaab
babbabba
Failure function
abaabaaab
\(\pi_{s}:0, 0, 1, 1, 2, 3, 4, 1, 2\)
怎麼找出這個表
暴力做可能需要\(O(N^3)\)
N個前綴,N次比較,每次比較長度為N
超級慢的啦
讓我們觀察一下怎麼樣讓他變好
觀察性質1-1
\(\pi[i+1]\leq\pi[i]+1\)
如果 \(\pi[i+1]=k\)
則代表\(s[0\sim k-1]=s[i-k+2\sim i+1]\)成立
那麼\(s[0\sim k-2]=s[i-k+2\sim i]\)必成立
故 \(\pi[i]\geq k-1\)
觀察性質1-2
這個性質可以讓我們的複雜度
從\(O(N^3)\)降低成\(O(N^2)\)
因為每一項到下一項最多只增加一
整個陣列最多只會增加\(N\)次(也最多減少\(N\)次
故每次從前一項加一往下找
只會匹配不到最多\(N\)次
觀察性質2-1
延續我們剛才的想法
什麼情況下\(\pi[i+1]=\pi[i]+1\)呢
就是\(s[i+1]=s[\pi [i]]\)的時候啊
那如果\(s[i+1]\neq s[\pi [i]]\)的時候怎麼辦
觀察性質2-2
我們希望找到最大的\(j\)使得
\(s[0\sim j-1]=s[i-j+2 \sim i+1]\)
我們只要找所有符合這個條件的\(j\)
再分別判斷\(s[j-1]=s[i+1]\)是否成立即可
這件事情成立的必要條件之一為
\(s[0\sim j-2]=s[i-j+2 \sim i]\)
觀察性質2-3
達成此條件最大的\(j_{max}=\pi [i]+1\)
\(s[0\sim j_{max}-2]=s[i-j_{max}+2 \sim i]\)
那麼剩下的\(j\)應該要符合以下條件
\(s[0\sim j-2]=s[i-j+2 \sim i]=s[j_{max}-j \sim j_{max}-2]\)
也就是下一個\(j\)值正巧就是
\(j=\pi [j_{max}-2]+1=\pi [\pi[i]-1]+1\)
那演算法就出來了欸
-
建陣列\(\pi [i]\),存第\(i\)個前綴的次長共同前後綴
-
初始化\(\pi [0]=0\)
-
若已經做完\(\pi [0]\sim \pi [i]\),令\(j=\pi [i]\)
-
若\(s[i+1]=s[j]\),則\(\pi [i+1]=j+1\)
-
否則更新\(j=\pi [j]\)
-
若\(j=0\),則\(\pi [i+1]=0\),否則重複執行迴圈
複雜度
根據前面性質1知道\(\pi [i]\)變化只有\(O(N)\)次
也就是説性質2中那個\(j\)的更新只需要\(O(N)\)次
又性質二只有每次更新\(j\)的時候才需要檢查字元
且每次只要檢查一個字元
故整體複雜度為\(O(N)\)
來字串匹配
簡單的版本:
要在字串\(s\)裏面找\(t\)
就對 \(t+\)"\(\$\)"\(+s\) 字串做一次failure function
然後觀察s中有哪些地方之\(\pi [i]=t.length()\)
\(O(n+m)\)字串匹配完成
另外一個版本
什麼是failure function,失敗在哪裡?
其實這個失敗函數的原意就是字串匹配失敗時
往前找尋下一個要從哪裡開始匹配的函數
就是原本已經匹配好的部分就不要再重複找了
那麼原本的字串匹配要怎麼做呢?
從s中一個字元一個字元跑
如果某個s中的字元匹配不到t中的下一個字元
就尋找t中最長的已經匹配好重複的區間
也就是次長共同前後綴
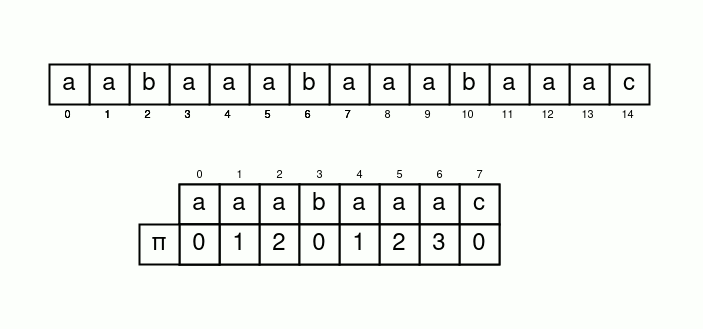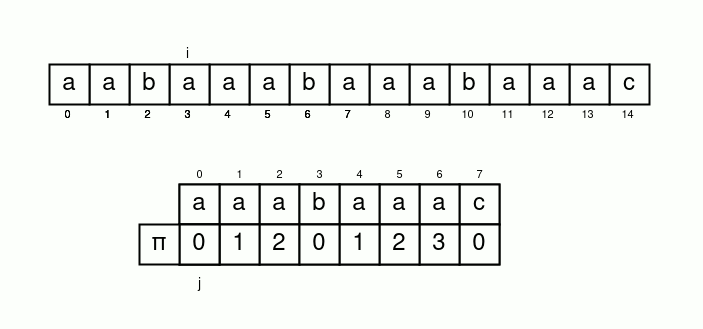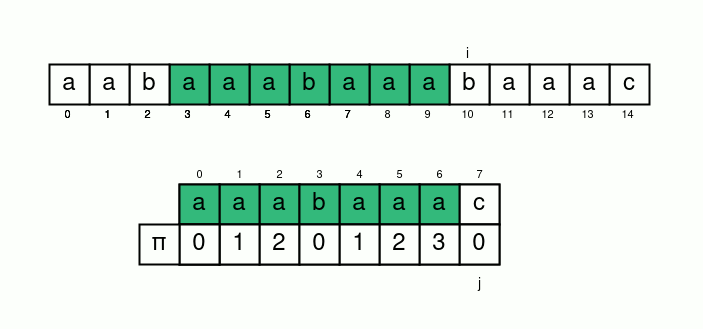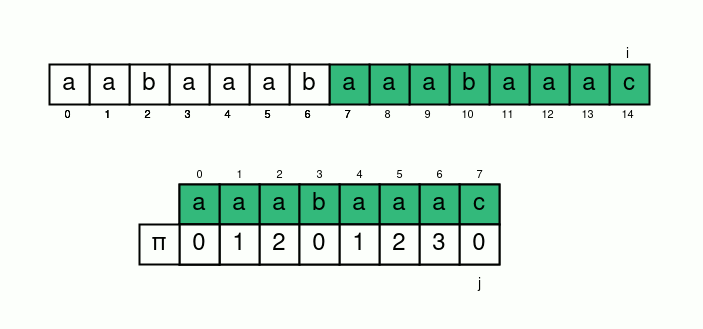
講得清楚一點
我們令一個變數 \(i\) 遍歷字串 \(s\)
並再令一個變數 \(j\) 表示 \(s[i]\) 應匹配的 \(t[j]\)
初始化 \(i=j=0\)
接下來只要 \(s[i]=t[j]\) 就 \(i, j\) 各加上 \(1\)
否則 \(j=\pi[j-1]\) 繼續匹配
複雜度證明
\(i, j\) 正好會增加 \(N\) 次
故 \(j\) 也只能減少 \(N\) 次
兩種操作皆只做 \(N\) 次
均攤複雜度 \(O(n)\)
扣的
#include <iostream>
#include <vector>
using namespace std;
#define ll long long
int main(){
vector<ll> ff;
ll n, m, cnt=0;
string a, b;
cin >> a;
n=a.length();
for(int w=0;w<1;w++){
cin >> b;
m=b.length();
ff.clear();
ff.pb(0);
for(int i=1;i<m;i++){
ff.pb(0);
ll j=i-1;
while(j>=0){
if(b[ff[j]]==b[i]){ff[i]=ff[j]+1;break;}
else j=ff[j]-1;
}
}
ll j=0;
for(int i=0;i<n;i++){
while(a[i]!=b[j] && j>0) j=ff[j-1];
if(j==0 && a[i]!=b[j]) continue;
j++;
if(j==m){
cnt++;
j=ff[j-1];
}
}
}
cout << cnt << endl;
return 0;
}題目
Z-algorithm
Z-algorithm字串匹配演算法的精髓
定義如下:
\(z[k]=\underset{i=0,1,...,n-k+1}{max}i\)
\(i:s[0\sim i-1]=s[k \sim k+i-1]\)
Z-function
WTF
這不是跟剛才那個
幾乎一模一樣嗎
剛才的東西用文字說明就是:
原字串跟從k開始的後綴的「最長共同前綴」
最長共同前綴
aabaaab
babbabba
Z-function
abaabaaab
\(z_{s}:0, 0, 1, 4, 0, 1, 1, 2, 0\)
怎麼找出這個表
暴力做可能需要\(O(N^2)\)
N個後綴,每次往後匹配長度為N
超級慢的啦
讓我們觀察一下怎麼樣讓他變好
通靈一下
我們先預設是跟failure function一樣由左往右找
可以用一個變數 \(r\) 記錄目前匹配到的最大右界
也就是 \(r=\underset{i=0, 1, ..., k-1}{max} (i+z[i]-1)\)
再記錄一下最大值發生時的左界 \(l\)
這可以幹嘛
於是我們會發現
假設我們目前要找 \(z[k]\)
如果\(k\leq r\)
\(z[k]\geq r-k+1 \cdots \cdots(1)\)
\(z[k]=z[k-l] \cdots \cdots(2)\)
\((1), (2)\) 至少有一個成立
也就是 \(z[k]\geq min(r-k+1, z[k-l])\)
白話文
因為\(s[0\sim r-l]=s[l\sim r]\)
當 \(l\leq k\leq r\) 時
如果 \(k-l+z[k-l]>r-l\)
那麼 \(z[k]\) 顯然大於等於 \(r-k+1\)
否則因爲 \(k-l+z[k-l]\) 不超過 \(r-l\)
那麼 \(z[k]\) 應該要等於 \(z[k-l]\)
所以呢
知道這個性質之後就直接暴力匹配就好了
啊為什麼會是好的
右界 \(r\) 最多只會增加 \(N\) 次
\(r\) 不增加的情況只有 \(k+z[k-l]<r\)
又此時我們可以 \(O(1)\) 算出\(z[k]=z[k-l]\)
故均攤 \(O(N)\)
來字串匹配
要做Z-function的字串匹配只有這個版本:
要在字串\(s\)裏面找\(t\)
就對 \(t+\)"\(\$\)"\(+s\) 字串做一次Z-function
然後觀察s中有哪些地方之\(z [i]=t.length()\)
\(O(n+m)\)字串匹配完成
扣的
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
#define ll long long
int main() {
ios_base::sync_with_stdio(0);cin.tie(0);
string s;
cin >> s;
ll n=s.length();
ll z[n], l=0, r=0;
fill(z, z+n, 0);
z[0]=0;
for(int i=1;i<n;i++){
if(i<=r) z[i]=min(r-i+1, z[i-l]);
while(i+z[i]<n && s[z[i]]==s[i+z[i]]) z[i]++;
if(i+z[i]-1>r) l=i, r=i+z[i]-1;
}
for(int i=0;i<n;i++) cout << z[i] << " ";cout << endl;
return 0;
}題目
Manacher
輸入一個字串,找出其中最長的回文子字串
\(|S|<10^6\)
CSES
Longest Palindrome
就正反Hash一下
枚舉迴文中心
二分搜迴文長度
阿不就做完了
複雜度\(O(nlogn)\)
你可能會想說
但是其實有更好的做法
要分成奇數迴文和偶數迴文好麻煩
那就先在每個字元中間夾一個特殊字元吧
首先考慮
abbabaaaba
*a*b*b*a*b*a*a*a*b*a*
接下來只需做迴文中心在字元上的case就好了
跟Z一樣建個怪陣列
*a*b*b*a*b*a*a*a*b*a*
\(f_{s}:0,1,0,1,2,1,0,1,0,3,0,1,2,7,2,1,0,1,0,1,0\)
\(f[i]=\) 以 \(s_{i}\) 為中心的最長迴文半徑
然後就跟Z很像了
紀錄 \(r\) 為目前找到迴文的最大右界
也就是 \(r=\underset{i=0, 1, ..., k-1}{max} (i+f[i])\)
並額外記錄最大值發生時的 \(mid=i\)
我們發現
假設我們目前要找 \(f[k]\)
如果\(k\leq r\)
\(f[k]\geq r-k \cdots \cdots(1)\)
\(f[k]=f[mid-(k-mid)] \cdots \cdots(2)\)
\((1), (2)\) 至少有一個成立
也就是 \(f[k]\geq min(r-k, f[mid-(k-mid)])\)
同樣的證明方法
右界 \(r\) 最多只會增加 \(N\) 次
\(r\) 不增加的情況只有 \(k+f[mid-(k-mid)]<r\)
又此時我們可以 \(O(1)\) 算出\(f[k]=f[mid-(k-mid)]\)
故均攤 \(O(N)\)
扣的
#include <iostream>
#include <algorithm>
using namespace std;
#define ll long long
int main() {
ios_base::sync_with_stdio(0);cin.tie(0);
string s, t;
cin >> s;
int n=s.length();
t=".";
for(int i=0;i<n;i++) t+=s[i],t+=".";
n=t.length();
int p[n], mid=-1, r=-1, ans=0;
fill(p, p+n, 0);
for(int i=0;i<n;i++){
if(i<=r) p[i]=min(p[2*mid-i], r-i);
for(int j=p[i]+1;j<=min(i,n-i-1);j++){
if(t[i+j]!=t[i-j]) break;
p[i]++;
}
if(p[i]>p[ans]) ans=i;
if(i+p[i]>r) r=i+p[i], mid=i;
}
for(int i=ans-p[ans]+1;i<=ans+p[ans];i+=2) cout << t[i];cout << endl;
return 0;
}題目
字串啦
By ck_platypus
字串啦
- 1,017



