Segment Tree
死線斷裂術
建北電資小社課 演算法
Segment Tree
線段樹
- 225班
- 電子計算機研習社_學術長
- 綽號807
這我

這建北電資
線段樹
線段樹
線段樹
怎麼分區間?
從中間切一半
1
5
5
8
4
3
7
2
6
13
7
9
19
16
35
若 \(n\) 為2的冪次
\(n\) 代表資料長度
如果資料長度不是2的冪次
1
5
8
4
3
7
2
1
13
7
9
14
16
30
這樣也行
若 \(n\) 非2的冪次
\(n\) 代表資料長度
- 建樹 : \(O(n log(n))\) 或 \(O(n)\)
- 查詢 : \(O(log(n))\)
- 修改 : \(O(log(n))\)
複雜度
複雜度比較
| 線段樹 | 前綴和 | 差分 | |
|---|---|---|---|
| 建表 |
|
||
| 區間查詢 | |||
| 單點修改 | |||
| 區間修改 |
\(O(n)\)
\(O(n)\)
\(O(log(n))\)
\(O(1)\)
\(O(n)\)
\(O(log(n))\)
\(O(n)\)
\(O(1)\)
\(O(log(n))\)
\(O(n)\)
\(O(1)\)
存樹
- 用 struct 存
- 左子節點指標
- 右子節點指標
- 值
指標型存法
struct node{
int value;
node *left, *right;
};- 開 4 倍大的陣列
- 以節點 \(x\)
- 左子節點位置 \(x \times 2\)
- 右子節點位置 \(x \times 2 + 1\)
陣列型存法 (偽指標型)
int n;
vector<int> data(n*4,0);註: \(n\) 代表原資料長度
4 倍 哪來的
若 \(n\) 為2的冪次
註: \(n\) 代表原資料長度
- 最下層有 \(n\) 個 (節點)
- 上層有 \(n \div 2\) 個
- 上上層有 \(n \div 2 \div 2\) 個
- 上上上層有 \(n \div 2 \div 2 \div 2\) 個
. . .
若 \(n\) 為2的冪次
註: \(n\) 代表原資料長度
- 有 \(log_2 n+1\) 層
- 需要 \(\frac{2^{log_2 n+1}-1}{2-1} \approx 2n \) 個 (節點)
若 \(n\) 不是 2的冪次
註: \(n\) 代表原資料長度
- \(n\) 到 \(2n\) 間有一個 \(n\) 的冪次
- 他需要的空間小於 \(2n \times 2 = 4n\)
- 我不會證明,你可以接受就好
- 開 2 倍大的陣列
- 以節點 \(x\)
- 左子節點位置 \(x \times 2\)
- 右子節點位置 \(x \times 2 + 1\)
迭代式線段樹陣列型存法
int n;
vector<int> data(n*2,0);註: \(n\) 代表原資料長度
2 倍 哪來的
有點複雜等等再說
建樹
Create
- 遞迴將左右子節點計算完
- 結和左右子節點值 (pull)
- 遞迴完就結束了
建樹 遞迴陣列型
線段樹 建樹 code
#include <bits/stdc++.h>
#define int long long
using namespace std;
struct SegmentTree {
int n;
vector<int> nodes;
SegmentTree()
: n(0) {
nodes.clear();
}
SegmentTree(vector<int> &data)
: n(data.size()) {
nodes.resize(n * 4);
build(data, 0, n);
}
void build(const vector<int> &data, int l, int r, int it = 1) {
if (r - l == 1) {
nodes[it] = data[l];
return;
}
int mid = (l + r) / 2;
build(data, l, mid, it * 2);
build(data, mid, r, it * 2 + 1);
nodes[it] = nodes[it * 2] + nodes[it * 2 + 1];
return;
}
};# PRESENTING CODE
初始化 nodes 大小
宣告 變數
到葉節點 複製值進去
取得中間值 區分左右子節點的區間
左區間在 \(x \times 2\)
右區間在 \(x \times 2 +1\)
遞迴計算子節點值
結合左右子節點值 (pull)
遞迴函式
還沒到葉節點
變數解釋
\(n\) 資料長度
\(nodes\) 節點值
\(data\) 原始資料
\(l\) \(r\) 左右邊界
\(mid\) 中介: 區分左右子區間
\(it\) 偽指標: 指向結點在\(nodes\)的位置
註: 皆為左閉右開 0-base
- 少於\(4n\) 個節點
- 每個節點只跑一次
- 複雜度: \(O(n)\)
複雜度分析
查詢
Read
- 遞迴下去做
- 三種可能
- 完全在左
- 完全在右
- 左右都有
查詢
線段樹 查詢 code
#include <bits/stdc++.h>
#define int long long
using namespace std;
struct SegmentTree {
int n;
vector<int> nodes;
SegmentTree()
: n(0) {
nodes.clear();
}
SegmentTree(vector<int> &data)
: n(data.size()) {
nodes.resize(n * 4);
build(data, 0, n);
}
void build(const vector<int> &data, int l, int r, int it = 1) {
if (r - l == 1) {
nodes[it] = data[l];
return;
}
int mid = (l + r) / 2;
build(data, l, mid, it * 2);
build(data, mid, r, it * 2 + 1);
nodes[it] = nodes[it * 2] + nodes[it * 2 + 1];
return;
}
int query(int queryL, int queryR, int l, int r, int it = 1) {
if (queryL == l && queryR == r) return nodes[it];
int mid = (l + r) / 2;
if (queryR <= mid)
return query(queryL, queryR, l, mid, it * 2);
else if (queryL >= mid)
return query(queryL, queryR, mid, r, it * 2 + 1);
else return query(queryL, mid, l, mid,
it * 2) +
query(mid, queryR, mid, r,
it * 2 + 1);
}
};# PRESENTING CODE
已經找到了
取得中間值 區分左右節點範圍
完全在左
完全在右
左右都有
左右都有
注意範圍
變數解釋
\(nodes\) 節點值
\(queryL\) \(queryR\) 搜尋左右界
\(l\) \(r\) 左右邊界
\(mid\) 中介: 區分左右子區間
\(it\) 偽指標: 指向結點在\(nodes\)的位置
註: 皆為左閉右開 0-base
- 他是好的
- 一層最多碰到4的節點
- 深度 : \(log(n)\)
- 複雜度 : \(O(log(n))\)
複雜度
單點修改
Update
線段樹 單點修改 code
#include <bits/stdc++.h>
#define int long long
using namespace std;
struct SegmentTree {
int n;
vector<int> nodes;
SegmentTree()
: n(0) {
nodes.clear();
}
SegmentTree(vector<int> &data)
: n(data.size()) {
nodes.resize(n * 4);
build(data, 0, n);
}
void build(const vector<int> &data, int l, int r, int it = 1) {
if (r - l == 1) {
nodes[it] = data[l];
return;
}
int mid = (l + r) / 2;
build(data, l, mid, it * 2);
build(data, mid, r, it * 2 + 1);
nodes[it] = nodes[it * 2] + nodes[it * 2 + 1];
return;
}
int query(int queryL, int queryR, int l, int r, int it = 1) {
if (queryL == l && queryR == r) return nodes[it];
int mid = (l + r) / 2;
if (queryR <= mid)
return query(queryL, queryR, l, mid, it * 2);
else if (queryL >= mid)
return query(queryL, queryR, mid, r, it * 2 + 1);
else return query(queryL, mid, l, mid,
it * 2) +
query(mid, queryR, mid, r,
it * 2 + 1);
}
void modify1(int pos, int modifyValue, int l, int r, int it = 1) {
if (r - l == 1) {
nodes[it] = modifyValue;
return;
}
int mid = (l + r) / 2;
if (pos < mid) modify1(pos, modifyValue, l, mid, it * 2);
else modify1(pos, modifyValue, mid, r, it * 2 + 1);
// pull
nodes[it] = nodes[it * 2] + nodes[it * 2 + 1];
return;
}
};# PRESENTING CODE
已經找到了 直接修改
取得中間值 區分左右節點範圍
在左
在右
修改目前節點值 (pull)
註: 皆為左閉右開 0-base
變數解釋
\(nodes\) 節點值
\(queryL\) \(queryR\) 搜尋左右界
\(l\) \(r\) 左右邊界
\(mid\) 中介: 區分左右子區間
\(it\) 偽指標: 指向結點在\(nodes\)的位置
- 改值後 pull 上來
- 複雜度就是最深深度
- 複雜度 \(O(log(n))\)
複雜度
多點修改
Update
- 懶人標記 (tag)
- 兩種做法
- 懶標下推 (推薦)
- 懶標永久化
懶標
線段樹 懶標下推 code
#include <bits/stdc++.h>
#define int long long
using namespace std;
struct SegmentTree {
int n;
vector<int> nodes;
vector<int> tags;
SegmentTree()
: n(0) {
nodes.clear();
tags.clear();
}
SegmentTree(vector<int> &data)
: n(data.size()) {
nodes.resize(n * 4);
tags.resize(n * 4);
build(data, 0, n);
}
void build(const vector<int> &data, int l, int r, int it = 1) {
if (r - l == 1) {
nodes[it] = data[l];
return;
}
int mid = (l + r) / 2;
build(data, l, mid, it * 2);
build(data, mid, r, it * 2 + 1);
nodes[it] = nodes[it * 2] + nodes[it * 2 + 1];
return;
}
void push(int l, int r, int it) {
int mid = (l + r) / 2;
nodes[it * 2] += tags[it] * (mid - l);
nodes[it * 2 + 1] += tags[it] * (r - mid);
tags[it * 2] += tags[it];
tags[it * 2 + 1] += tags[it];
tags[it] = 0;
return;
}
int query(int queryL, int queryR, int l, int r, int it = 1) {
if (queryL == l && queryR == r) return nodes[it];
push(l, r, it);
int mid = (l + r) / 2;
if (queryR <= mid)
return query(queryL, queryR, l, mid, it * 2);
else if (queryL >= mid)
return query(queryL, queryR, mid, r, it * 2 + 1);
else return query(queryL, mid, l, mid,
it * 2) +
query(mid, queryR, mid, r,
it * 2 + 1);
}
void modify(int modifyL, int modifyR, int delta,
int l, int r, int it = 1) {
if (modifyL == l && modifyR == r) {
nodes[it] += delta * (r - l);
tags[it] += delta;
return;
}
push(l, r, it);
int mid = (l + r) / 2;
if (modifyR <= mid)
modify(modifyL, modifyR, delta, l, mid, it * 2);
else if (modifyL >= mid)
modify(modifyL, modifyR, delta, mid, r, it * 2 + 1);
else {
modify(modifyL, mid, delta, l, mid, it * 2);
modify(mid, modifyR, delta, mid, r, it * 2 + 1);
}
// pull
nodes[it] = nodes[it * 2] + nodes[it * 2 + 1];
return;
}
};# PRESENTING CODE
新增宣告 tags (懶標)
build 函式 不需要改
註: 皆為左閉右開 0-base
變數解釋
\(nodes\) 節點值
\(tags\) 懶標值
\(l\) \(r\) 左右邊界
\(mid\) 中介: 區分左右子區間
\(it\) 偽指標: 指向結點在\(nodes\)的位置
線段樹 懶標下推 code push()
#include <bits/stdc++.h>
#define int long long
using namespace std;
struct SegmentTree {
int n;
vector<int> nodes;
vector<int> tags;
SegmentTree()
: n(0) {
nodes.clear();
tags.clear();
}
SegmentTree(vector<int> &data)
: n(data.size()) {
nodes.resize(n * 4);
tags.resize(n * 4);
build(data, 0, n);
}
void build(const vector<int> &data, int l, int r, int it = 1) {
if (r - l == 1) {
nodes[it] = data[l];
return;
}
int mid = (l + r) / 2;
build(data, l, mid, it * 2);
build(data, mid, r, it * 2 + 1);
nodes[it] = nodes[it * 2] + nodes[it * 2 + 1];
return;
}
void push(int l, int r, int it) {
int mid = (l + r) / 2;
nodes[it * 2] += tags[it] * (mid - l);
nodes[it * 2 + 1] += tags[it] * (r - mid);
tags[it * 2] += tags[it];
tags[it * 2 + 1] += tags[it];
tags[it] = 0;
return;
}
int query(int queryL, int queryR, int l, int r, int it = 1) {
if (queryL == l && queryR == r) return nodes[it];
push(l, r, it);
int mid = (l + r) / 2;
if (queryR <= mid)
return query(queryL, queryR, l, mid, it * 2);
else if (queryL >= mid)
return query(queryL, queryR, mid, r, it * 2 + 1);
else return query(queryL, mid, l, mid,
it * 2) +
query(mid, queryR, mid, r,
it * 2 + 1);
}
void modify(int modifyL, int modifyR, int delta,
int l, int r, int it = 1) {
if (modifyL == l && modifyR == r) {
nodes[it] += delta * (r - l);
tags[it] += delta;
return;
}
push(l, r, it);
int mid = (l + r) / 2;
if (modifyR <= mid)
modify(modifyL, modifyR, delta, l, mid, it * 2);
else if (modifyL >= mid)
modify(modifyL, modifyR, delta, mid, r, it * 2 + 1);
else {
modify(modifyL, mid, delta, l, mid, it * 2);
modify(mid, modifyR, delta, mid, r, it * 2 + 1);
}
// pull
nodes[it] = nodes[it * 2] + nodes[it * 2 + 1];
return;
}
};# PRESENTING CODE
需要知道 子節點範圍
左右子節點都加上
\(懶標 \times 範圍大小\)
更新子節點懶標
懶標歸0
push 完成
註: 皆為左閉右開 0-base
變數解釋
\(nodes\) 節點值
\(tags\) 懶標值
\(l\) \(r\) 左右邊界
\(mid\) 中介: 區分左右子區間
\(it\) 偽指標: 指向結點在\(nodes\)的位置
線段樹 懶標下推 code query()
#include <bits/stdc++.h>
#define int long long
using namespace std;
struct SegmentTree {
int n;
vector<int> nodes;
vector<int> tags;
SegmentTree()
: n(0) {
nodes.clear();
tags.clear();
}
SegmentTree(vector<int> &data)
: n(data.size()) {
nodes.resize(n * 4);
tags.resize(n * 4);
build(data, 0, n);
}
void build(const vector<int> &data, int l, int r, int it = 1) {
if (r - l == 1) {
nodes[it] = data[l];
return;
}
int mid = (l + r) / 2;
build(data, l, mid, it * 2);
build(data, mid, r, it * 2 + 1);
nodes[it] = nodes[it * 2] + nodes[it * 2 + 1];
return;
}
void push(int l, int r, int it) {
int mid = (l + r) / 2;
nodes[it * 2] += tags[it] * (mid - l);
nodes[it * 2 + 1] += tags[it] * (r - mid);
tags[it * 2] += tags[it];
tags[it * 2 + 1] += tags[it];
tags[it] = 0;
return;
}
int query(int queryL, int queryR, int l, int r, int it = 1) {
if (queryL == l && queryR == r) return nodes[it];
push(l, r, it);
int mid = (l + r) / 2;
if (queryR <= mid)
return query(queryL, queryR, l, mid, it * 2);
else if (queryL >= mid)
return query(queryL, queryR, mid, r, it * 2 + 1);
else return query(queryL, mid, l, mid,
it * 2) +
query(mid, queryR, mid, r,
it * 2 + 1);
}
void modify(int modifyL, int modifyR, int delta,
int l, int r, int it = 1) {
if (modifyL == l && modifyR == r) {
nodes[it] += delta * (r - l);
tags[it] += delta;
return;
}
push(l, r, it);
int mid = (l + r) / 2;
if (modifyR <= mid)
modify(modifyL, modifyR, delta, l, mid, it * 2);
else if (modifyL >= mid)
modify(modifyL, modifyR, delta, mid, r, it * 2 + 1);
else {
modify(modifyL, mid, delta, l, mid, it * 2);
modify(mid, modifyR, delta, mid, r, it * 2 + 1);
}
// pull
nodes[it] = nodes[it * 2] + nodes[it * 2 + 1];
return;
}
};# PRESENTING CODE
每次到了就下推
註: 皆為左閉右開 0-base
變數解釋
\(nodes\) 節點值
\(queryL\) \(queryR\) 搜尋左右界
\(l\) \(r\) 左右邊界
\(mid\) 中介: 區分左右子區間
\(it\) 偽指標: 指向結點在\(nodes\)的位置
線段樹 懶標下推 code modify()
#include <bits/stdc++.h>
#define int long long
using namespace std;
struct SegmentTree {
int n;
vector<int> nodes;
vector<int> tags;
SegmentTree()
: n(0) {
nodes.clear();
tags.clear();
}
SegmentTree(vector<int> &data)
: n(data.size()) {
nodes.resize(n * 4);
tags.resize(n * 4);
build(data, 0, n);
}
void build(const vector<int> &data, int l, int r, int it = 1) {
if (r - l == 1) {
nodes[it] = data[l];
return;
}
int mid = (l + r) / 2;
build(data, l, mid, it * 2);
build(data, mid, r, it * 2 + 1);
nodes[it] = nodes[it * 2] + nodes[it * 2 + 1];
return;
}
void push(int l, int r, int it) {
int mid = (l + r) / 2;
nodes[it * 2] += tags[it] * (mid - l);
nodes[it * 2 + 1] += tags[it] * (r - mid);
tags[it * 2] += tags[it];
tags[it * 2 + 1] += tags[it];
tags[it] = 0;
return;
}
int query(int queryL, int queryR, int l, int r, int it = 1) {
if (queryL == l && queryR == r) return nodes[it];
push(l, r, it);
int mid = (l + r) / 2;
if (queryR <= mid)
return query(queryL, queryR, l, mid, it * 2);
else if (queryL >= mid)
return query(queryL, queryR, mid, r, it * 2 + 1);
else return query(queryL, mid, l, mid,
it * 2) +
query(mid, queryR, mid, r,
it * 2 + 1);
}
void modify(int modifyL, int modifyR, int delta,
int l, int r, int it = 1) {
if (modifyL == l && modifyR == r) {
nodes[it] += delta * (r - l);
tags[it] += delta;
return;
}
push(l, r, it);
int mid = (l + r) / 2;
if (modifyR <= mid)
modify(modifyL, modifyR, delta, l, mid, it * 2);
else if (modifyL >= mid)
modify(modifyL, modifyR, delta, mid, r, it * 2 + 1);
else {
modify(modifyL, mid, delta, l, mid, it * 2);
modify(mid, modifyR, delta, mid, r, it * 2 + 1);
}
// pull
nodes[it] = nodes[it * 2] + nodes[it * 2 + 1];
return;
}
};# PRESENTING CODE
如果範圍正確
更新此節點值
加上懶標
有點像單點修改+區間查詢
下推
完全在左
完全在右
取得中間值
左右都有
修改目前節點值 (pull)
註: 皆為左閉右開 0-base
變數解釋
\(nodes\) 節點值
\(tags\) 懶標值
\(modifyL\) \(modifyR\) 修改左右區間
\(delta\) 修改增加值
複雜度
補充
迭代式線段樹
- 節省一半記憶體
- 常數小
- \(O(n)\) 建樹 \(\leftrightarrow\) 遞迴式線段樹
- 有點懸的存圖
- code 短
優點
存圖方式 \(n\) 為2的冪次
註: \(n\) 代表原資料長度
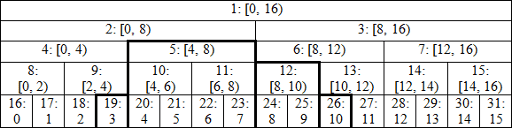
迭代式線段樹 存圖 code
#include <bits/stdc++.h>
#define int long long
using namespace std;
struct SegmentTree {
int n;
vector<int> nodes;
SegmentTree()
: n(0) {
nodes.clear();
}
SegmentTree(vector<int> &data)
: n(data.size()) {
nodes.resize(n << 1);
build(data);
}
void build(const vector<int> &data) {
for (int i = n; i--;) nodes[i + n] = data[i];
for (int i = n; i--;)
nodes[i] = nodes[i << 1] + nodes[i << 1 | 1];
return;
}
void pull(int pos) {
for (pos += n; pos >>= 1;)
nodes[pos] = nodes[pos << 1] + nodes[pos << 1 | 1];
return;
}
int query(int l, int r) {
int sum = 0;
for (l += n, r += n; l < r; l >>= 1, r >>= 1) {
if (l & 1) sum += nodes[l++];
if (r & 1) sum += nodes[--r];
}
return sum;
}
void modify1(int pos, int modifyValue) {
nodes[pos + n] = modifyValue;
pull(pos);
return;
}
};# PRESENTING CODE
迭代式線段樹 build code
#include <bits/stdc++.h>
#define int long long
using namespace std;
struct SegmentTree {
int n;
vector<int> nodes;
SegmentTree()
: n(0) {
nodes.clear();
}
SegmentTree(vector<int> &data)
: n(data.size()) {
nodes.resize(n << 1);
build(data);
}
void build(const vector<int> &data) {
for (int i = n; i--;) nodes[i + n] = data[i];
for (int i = n; i--;)
nodes[i] = nodes[i << 1] + nodes[i << 1 | 1];
return;
}
void pull(int pos) {
for (pos += n; pos >>= 1;)
nodes[pos] = nodes[pos << 1] + nodes[pos << 1 | 1];
return;
}
int query(int l, int r) {
int sum = 0;
for (l += n, r += n; l < r; l >>= 1, r >>= 1) {
if (l & 1) sum += nodes[l++];
if (r & 1) sum += nodes[--r];
}
return sum;
}
void modify1(int pos, int modifyValue) {
nodes[pos + n] = modifyValue;
pull(pos);
return;
}
};# PRESENTING CODE
迭代式線段樹 query code
#include <bits/stdc++.h>
#define int long long
using namespace std;
struct SegmentTree {
int n;
vector<int> nodes;
SegmentTree()
: n(0) {
nodes.clear();
}
SegmentTree(vector<int> &data)
: n(data.size()) {
nodes.resize(n << 1);
build(data);
}
void build(const vector<int> &data) {
for (int i = n; i--;) nodes[i + n] = data[i];
for (int i = n; i--;)
nodes[i] = nodes[i << 1] + nodes[i << 1 | 1];
return;
}
void pull(int pos) {
for (pos += n; pos >>= 1;)
nodes[pos] = nodes[pos << 1] + nodes[pos << 1 | 1];
return;
}
int query(int l, int r) {
int sum = 0;
for (l += n, r += n; l < r; l >>= 1, r >>= 1) {
if (l & 1) sum += nodes[l++];
if (r & 1) sum += nodes[--r];
}
return sum;
}
void modify1(int pos, int modifyValue) {
nodes[pos + n] = modifyValue;
pull(pos);
return;
}
};# PRESENTING CODE
迭代式線段樹 單點修改 code
#include <bits/stdc++.h>
#define int long long
using namespace std;
struct SegmentTree {
int n;
vector<int> nodes;
SegmentTree()
: n(0) {
nodes.clear();
}
SegmentTree(vector<int> &data)
: n(data.size()) {
nodes.resize(n << 1);
build(data);
}
void build(const vector<int> &data) {
for (int i = n; i--;) nodes[i + n] = data[i];
for (int i = n; i--;)
nodes[i] = nodes[i << 1] + nodes[i << 1 | 1];
return;
}
void pull(int pos) {
for (pos += n; pos >>= 1;)
nodes[pos] = nodes[pos << 1] + nodes[pos << 1 | 1];
return;
}
int query(int l, int r) {
int sum = 0;
for (l += n, r += n; l < r; l >>= 1, r >>= 1) {
if (l & 1) sum += nodes[l++];
if (r & 1) sum += nodes[--r];
}
return sum;
}
void modify1(int pos, int modifyValue) {
nodes[pos + n] = modifyValue;
pull(pos);
return;
}
};# PRESENTING CODE
- 一樣要懶標
多點修改
迭代式線段樹 code 懶標
#include <bits/stdc++.h>
#define int long long
using namespace std;
struct SegmentTree {
int n;
vector<int> nodes;
vector<int> tags;
SegmentTree()
: n(0) {
nodes.clear();
tags.clear();
}
SegmentTree(vector<int> &data)
: n(data.size()) {
nodes.resize(n << 1, 0);
tags.resize(n, 0);
build(data);
}
void build(const vector<int> &data) {
for (int i = n; i--;) nodes[i + n] = data[i];
for (int i = n; i--;)
nodes[i] = nodes[i << 1] + nodes[i << 1 | 1];
return;
}
void pull(int pos) {
pos += n;
for (int h = 1; pos >>= 1; h++)
nodes[pos] = nodes[pos << 1] + nodes[pos << 1 | 1] +
(tags[pos] << h);
return;
}
void push(int pos) {
pos += n;
for (int h = __lg(pos), it = 1; h--; it = pos >> h) {
if (!tags[it]) continue;
nodes[it << 1] += tags[it] << h;
nodes[it << 1 | 1] += tags[it] << h;
if (h) {
tags[it << 1] += tags[it];
tags[it << 1 | 1] += tags[it];
}
tags[it] = 0;
}
}
int query(int l, int r) {
push(l), push(r - 1);
int sum = 0;
for (l += n, r += n; l < r; l >>= 1, r >>= 1) {
if (l & 1) sum += nodes[l++];
if (r & 1) sum += nodes[--r];
}
return sum;
}
void modify(int l, int r, int delta) {
push(l), push(r - 1);
int l2 = l + n, r2 = r + n;
if (l2 & 1) nodes[l2++] += delta;
if (r2 & 1) nodes[--r2] += delta;
for (int h = 1; (l2 >>= 1) < (r2 >>= 1); h++) {
if (l2 & 1) tags[l2] += delta, nodes[l2++] += delta << h;
if (r2 & 1) tags[--r2] += delta, nodes[r2] += delta << h;
}
pull(l), pull(r - 1);
}
};
signed main() {
int n, q;
cin >> n >> q;
vector<int> data(n);
for (int &i : data) cin >> i;
SegmentTree st(data);
for (int mode, l, r, delta; q--;) {
cin >> mode;
if (mode == 1) {
cin >> l >> r >> delta;
st.modify(l - 1, r, delta);
}
else {
cin >> l;
cout << st.query(l - 1, l) << "\n";
}
}
}# PRESENTING CODE
指標型線段樹
指標型線段樹
#include <bits/stdc++.h>
#define int long long
using namespace std;
struct node {
int l, r;
int value = 0, tag = 0;
node *pointerL = nullptr, *pointerR = nullptr;
node(int _l, int _r)
: l(_l), r(_r) {}
node(vector<int> &data) {
l = 0;
r = data.size();
build(data);
}
void build(const vector<int> &data) {
if (r - l == 1) {
value = data[l];
return;
}
int mid = l + r >> 1;
pointerL = new node(l, mid);
pointerR = new node(mid, r);
pointerL->build(data);
pointerR->build(data);
value = pointerL->value + pointerR->value;
return;
}
void push() {
if (r - l == 1) return;
pointerL->value += tag * (pointerL->r - l);
pointerR->value += tag * (r - pointerR->l);
pointerL->tag += tag;
pointerR->tag += tag;
tag = 0;
}
int query(int queryL, int queryR) {
if (queryL == l && queryR == r) return value;
push();
if (queryR <= pointerL->r)
return pointerL->query(queryL, queryR);
else if (queryL >= pointerR->l)
return pointerR->query(queryL, queryR);
else return pointerL->query(queryL, pointerL->r) +
pointerR->query(pointerR->l, queryR);
}
void modify(int modifyL, int modifyR, int delta) {
if (modifyL == l && modifyR == r) {
value += delta * (r - l);
tag += delta;
return;
}
push();
if (modifyR <= pointerL->r)
pointerL->modify(modifyL, modifyR, delta);
else if (modifyL >= pointerR->l)
pointerR->modify(modifyL, modifyR, delta);
else {
pointerL->modify(modifyL, pointerL->r, delta);
pointerR->modify(pointerR->l, modifyR, delta);
}
// pull
value = pointerL->value + pointerR->value;
return;
}
};
signed main() {
int n, q;
cin >> n >> q;
vector<int> data(n);
for (int &i : data) cin >> i;
node st(data);
for (int mode, l, r, u, k; q--;) {
cin >> mode;
if (mode == 1) {
cin >> l >> r >> u;
st.modify(l - 1, r, u);
}
else {
cin >> k;
cout << st.query(k - 1, k) << "\n";
}
}
}# PRESENTING CODE
平衡二元樹
- 二元
- 樹
二元樹
🌲
樹 結構
根節點
葉節點
分支
根節點的
子節點
- 節點 + 分支
- 根節點 : 節點根源
- 葉節點 : 無子節點
- 子節點 : 向下連結到的
- 深度 : 根到此節點的路徑長
樹結構
樹 結構
根節點
葉節點
分支
根節點的
子節點
- 每個節點至多 2 個子節點
二元樹
二元?
至多兩個子節點
二元樹 結構
根節點
葉節點
根節點的
子節點
分支
SegmentTree
By 建中店自計算機研習社學術長807⁸⁰⁷
SegmentTree
- 489



