Performance and Functional Programming with Rust

Clint Liddick

07/13/2016

Pittsburgh Functional Programming Meetup

HERB

Mathematics provides a framework for dealing precisely with notions of ``what is.'' Computation provides a framework for dealing precisely with notions of ``how to.''

- Structure and Interpretation of Computer Programs

Universal Turing Machine

Von Neumann Architecture

Performance

  • Short response time for a given piece of work

  • High throughput (rate of processing work)

  • Low utilization of computing resource(s)

  • High availability of the computing system or application

  • Fast (or highly compact) data compression and decompression

  • High bandwidth

  • Short data transmission time

worse

better

unacceptable

adds value

adds no value

how

what

#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
 
bool is_sorted(int *a, int n)
{
  while ( --n >= 1 ) {
    if ( a[n] < a[n-1] ) return false;
  }
  return true;
}
 
void shuffle(int *a, int n)
{
  int i, t, r;
  for(i=0; i < n; i++) {
    t = a[i];
    r = rand() % n;
    a[i] = a[r];
    a[r] = t;
  }
}
 
void sort(int *a, int n)
{
  while ( !is_sorted(a, n) ) shuffle(a, n);
}

how

what

void quick_sort (int *a, int n) {
    int i, j, p, t;
    if (n < 2)
        return;
    p = a[n / 2];
    for (i = 0, j = n - 1;; i++, j--) {
        while (a[i] < p)
            i++;
        while (p < a[j])
            j--;
        if (i >= j)
            break;
        t = a[i];
        a[i] = a[j];
        a[j] = t;
    }
    quick_sort(a, i);
    quick_sort(a + i, n - i);
}
def quickSort(arr):
    less = []
    pivotList = []
    more = []
    if len(arr) <= 1:
        return arr
    else:
        pivot = arr[0]
        for i in arr:
            if i < pivot:
                less.append(i)
            elif i > pivot:
                more.append(i)
            else:
                pivotList.append(i)
        less = quickSort(less)
        more = quickSort(more)
        return less + pivotList + more
fn quick_sort<T>(v: &mut [T], f: &OrderFunc<T>) {
 
    let len = v.len();
    if len < 2 {
        return;
    }
 
    let pivot_index = partition(v, f);
 
    // Sort the left side
    quick_sort(&mut v[0..pivot_index], f);
 
    // Sort the right side
    quick_sort(&mut v[pivot_index + 1..len], f);
}
 
fn partition<T>(v: &mut [T], f: &OrderFunc<T>) -> usize {
    let len = v.len();
    let pivot_index = len / 2;
 
    v.swap(pivot_index, len - 1);
 
    let mut store_index = 0;
    for i in 0..len - 1 {
        if f(&v[i], &v[len - 1]) {
            v.swap(i, store_index);
            store_index += 1;
        }
    }
 
    v.swap(store_index, len - 1);
    store_index
}
qsort [] = []
qsort (x:xs) = qsort [y | y <- xs, y < x] ++ [x] ++ qsort [y | y <- xs, y >= x]
(defn qsort [[pivot & xs]]
  (when pivot
    (let [smaller #(< % pivot)]
      (lazy-cat (qsort (filter smaller xs))
		[pivot]
		(qsort (remove smaller xs))))))

how

what

Rust is a systems programming language that runs blazingly fast, prevents segfaults, and guarantees thread safety.

 

Featuring

  • zero-cost abstractions

  • move semantics

  • guaranteed memory safety

  • threads without data races

  • trait-based generics

  • pattern matching

  • type inference

  • minimal runtime

  • efficient C bindings 

fn main() {
    // A simple integer calculator:
    // `+` or `-` means add or subtract by 1
    // `*` or `/` means multiply or divide by 2

    let program = "+ + * - /";
    let mut accumulator = 0;

    for token in program.chars() {
        match token {
            '+' => accumulator += 1,
            '-' => accumulator -= 1,
            '*' => accumulator *= 2,
            '/' => accumulator /= 2,
            _ => { /* ignore everything else */ }
        }
    }

    println!("The program \"{}\" calculates the value {}",
              program, accumulator);
}

https://www.rust-lang.org

fn main() {
    let program = "+ + * - /";
    let value = program.chars().fold(0, |acc, x| {
        match x {
            '+' => acc + 1,
            '-' => acc - 1,
            '*' => acc * 2,
            '/' => acc / 2,
            _ => acc,
        }
    });

    println!("The program \"{}\" calculates the value {}", program, value);
}
struct CalcExpression {
    value: i32,
}

impl CalcExpression {
    fn new() -> CalcExpression {
        CalcExpression { value: 0 }
    }

    fn add(&mut self) {
        self.value += 1;
    }

    fn sub(&mut self) {
        self.value -= 1;
    }

    fn mult(&mut self) {
        self.value *= 2;
    }

    fn div(&mut self) {
        self.value /= 2;
    }
}

fn main() {
    let program = "+ + * - /";
    let mut expr = CalcExpression::new();

    for token in program.chars() {
        match token {
            '+' => expr.add(),
            '-' => expr.sub(),
            '*' => expr.mult(),
            '/' => expr.div(),
              _ => { /* ignore everything else */ }
        }
    }

    println!("The program \"{}\" calculates the value {}",
    program, expr.value);
}
trait Random {
  fn rand(&self) -> i64;
}

struct xkcd;

impl Random for xkcd {
  fn rand(&self) -> i64 {
  4 // chosen by fair dice role.
  // guaranteed to be random.
  }
}

fn print_5_rands<T: Random>(gen: &T) {
  for _ in 0..5 {
  println!("{}", gen.rand());
  }
}

fn main() {
  let r = xkcd;
  print_5_rands(&r);
}
section     .text
global      _start

_start:                        

    mov     edx,len            
    mov     ecx,msg            
    mov     ebx,1              
    mov     eax,4              
    int     0x80               

    mov     eax,1              
    int     0x80               

section     .data

msg     db  'Hello, world!',0xa
len     equ $ - msg
print("Hello, world!")

zero-overhead principle

What you don’t use, you don’t pay for.  And further:  What you do use, you couldn’t hand code any better.

Bjarne Stroustrup: Foundations of C++

Memory

stack

heap

OS

allocated

free

struct foo *ptr;
ptr = (struct foo *) malloc (sizeof (struct foo));  // allocate and cast
if (ptr == 0) abort();  // you could fail
memset (ptr, 0, sizeof (struct foo));  
// clearing the memory is best practice, not required
use std::mem;

#[derive(Clone, Copy)]
struct Point {
    x: f64,
    y: f64,
}

#[allow(dead_code)]
struct Rectangle {
    p1: Point,
    p2: Point,
}

fn origin() -> Point {
    Point { x: 0.0, y: 0.0 }
}

fn boxed_origin() -> Box<Point> {
    // Allocate this point in the heap, and return a pointer to it
    Box::new(Point { x: 0.0, y: 0.0 })
}

fn main() {
    // (all the type annotations are superfluous)
    // Stack allocated variables
    let point: Point = origin();
    let rectangle: Rectangle = Rectangle {
        p1: origin(),
        p2: Point { x: 3.0, y: 4.0 },
    };

    // Heap allocated rectangle
    let boxed_rectangle: Box<Rectangle> = Box::new(Rectangle {
        p1: origin(),
        p2: origin(),
    });

    // The output of functions can be boxed
    let boxed_point: Box<Point> = Box::new(origin());

    // Double indirection
    let box_in_a_box: Box<Box<Point>> = Box::new(boxed_origin());

    println!("Point occupies {} bytes in the stack",
             mem::size_of_val(&point));
    println!("Rectangle occupies {} bytes in the stack",
             mem::size_of_val(&rectangle));

    // box size = pointer size
    println!("Boxed point occupies {} bytes in the stack",
             mem::size_of_val(&boxed_point));
    println!("Boxed rectangle occupies {} bytes in the stack",
             mem::size_of_val(&boxed_rectangle));
    println!("Boxed box occupies {} bytes in the stack",
             mem::size_of_val(&box_in_a_box));

    // Copy the data contained in `boxed_point` into `unboxed_point`
    let unboxed_point: Point = *boxed_point;
    println!("Unboxed point occupies {} bytes in the stack",
             mem::size_of_val(&unboxed_point));
}

http://rustbyexample.com/std/box.html

Memory

stack

heap

OS

allocated

free

icons by Rob Armes, Michael Zick Doherty for The Noun Project

#include <memory>

namespace totallyrad
{

struct HugeData {
  int x;
  // ...
};

class DataHandler
{
public:
  DataHandler() { data = new HugeData(); };

  ~DataHandler() { delete data; };

private:
  HugeData* data;
};

}

int main()
{
  totallyrad::DataHandler d;
  return 0;
}

use std::mem;

#[derive(Clone, Copy)]
struct Point {
    x: f64,
    y: f64,
}

#[allow(dead_code)]
struct Rectangle {
    p1: Point,
    p2: Point,
}

fn origin() -> Point {
    Point { x: 0.0, y: 0.0 }
}

fn boxed_origin() -> Box<Point> {
    // Allocate this point in the heap, and return a pointer to it
    Box::new(Point { x: 0.0, y: 0.0 })
}

fn main() {
    // (all the type annotations are superfluous)
    // Stack allocated variables
    let point: Point = origin();
    let rectangle: Rectangle = Rectangle {
        p1: origin(),
        p2: Point { x: 3.0, y: 4.0 },
    };

    // Heap allocated rectangle
    let boxed_rectangle: Box<Rectangle> = Box::new(Rectangle {
        p1: origin(),
        p2: origin(),
    });

    // The output of functions can be boxed
    let boxed_point: Box<Point> = Box::new(origin());

    // Double indirection
    let box_in_a_box: Box<Box<Point>> = Box::new(boxed_origin());

    println!("Point occupies {} bytes in the stack",
             mem::size_of_val(&point));
    println!("Rectangle occupies {} bytes in the stack",
             mem::size_of_val(&rectangle));

    // box size = pointer size
    println!("Boxed point occupies {} bytes in the stack",
             mem::size_of_val(&boxed_point));
    println!("Boxed rectangle occupies {} bytes in the stack",
             mem::size_of_val(&boxed_rectangle));
    println!("Boxed box occupies {} bytes in the stack",
             mem::size_of_val(&box_in_a_box));

    // Copy the data contained in `boxed_point` into `unboxed_point`
    let unboxed_point: Point = *boxed_point;
    println!("Unboxed point occupies {} bytes in the stack",
             mem::size_of_val(&unboxed_point));
}

http://rustbyexample.com/std/box.html

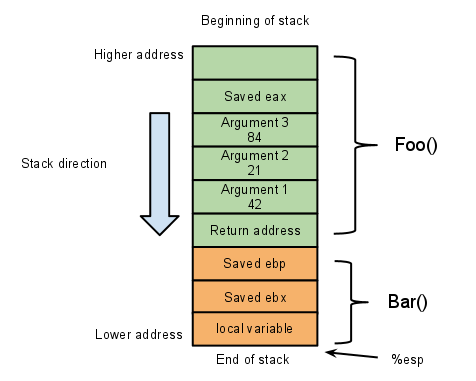
Value vs. Reference

Value vs. Reference

5

0xdf

0xde

0xdd

0xdc

0x87

0x87

0x86

0x85

0x84

...

...

char value

long reference

long value

9223372036854775807
def add_one(x):
    return x + 1
public static int addOne(int x) {
    return x + 1;
}
addOne   :: (Integral a) => a
addOne x = x + 1
function add_one(x) {
    return x + 1;
}
struct Huge {
    x: f64,
    // all the data
}

// take by reference
fn analyze_data(data: &Huge) -> f64 {
    data.x
}

fn main() {
    let h = Huge { x: 1.5 };
    let res = analyze_data(&h);
    println!("{}", res);
}
def add_one(x):
    return x + 1
public static int addOne(int x) {
    return x + 1;
}
addOne   :: (Integral a) => a
addOne x = x + 1
function add_one(x) {
    return x + 1;
}
def add_one(x):
    return x + 1
public static int addOne(int x) {
    return x + 1;
}
addOne   :: (Integral a) => a
addOne x = x + 1
function add_one(x) {
    return x + 1;
}
def find(arr, item):
    bogosort(arr)  // fuck you
    for idx, val in enumerate(arr):
        if val is item:
            return idx
    return -1
#[derive(Clone)]
struct Huge {
    x: i64,
    // ...
}

fn immut_transform(data: &Huge) -> Huge {
    let mut new_data = data.clone();
    new_data.x += 1;
    new_data  // NOT moved efficiently :-(
}

fn main() {
    let old_data = Huge { x: 1 };
    let new_data = immut_transform(&old_data);
    println!("old: {}", old_data.x);
    println!("new: {}", new_data.x);
}
impl Huge {
     fn new(x: i64) -> Huge {
          Huge { x: x }
     }
}

fn main() {
     let h = Huge::new(12);
}
struct Huge {
    x: i64,
    // ...
}

fn functional_transform(data: &mut Huge) -> &Huge {
    data.x += 1;
    data
}

fn main() {
    let mut fn_data = Huge { x: 1 };
    let fn_data = functional_transform(&mut fn_data);
    println!("func: {}", fn_data.x);
}
struct Huge {
    x: i64,
    // ...
}

fn procedural_transform(data: &mut Huge) -> &mut Huge {
    data.x += 1;
    data
}

fn main() {
    let mut proc_data = Huge { x: 1 };
    procedural_transform(procedural_transform(&mut proc_data));
    println!("proc: {}", proc_data.x);
}

icons by Alex Krummenacher and Josh Sorosky for The Noun Project

use std::thread;

struct Data {
    x: i64
}

fn main() {
    let d = Data { x: 1 };
    thread::spawn(|| {
        println!("x is {}", d.x);  // ERROR
    });
}
use std::thread;

struct Data {
    x: i64
}

fn main() {
    let d = Data { x: 1 };
    thread::spawn(move || {
        println!("x is {}", d.x);
    });

    println!("x is {}", d.x); // ERROR
}
{d \over dt} ({\partial T \over \partial \dot{q_j} }) - {\partial T \over \partial q_j } + {\partial V \over \partial q_j } - Q_j = 0
ddt(∂T∂qj˙)−∂T∂qj+∂V∂qj−Qj=0{d \over dt} ({\partial T \over \partial \dot{q_j} }) - {\partial T \over \partial q_j } + {\partial V \over \partial q_j } - Q_j = 0

where:

T is kinetic energy

V is potential energy

q is position

Strictness / Laziness

a + (b + c)
#include <iostream>

struct Data {
  bool val;
};

int main()
{
  Data *d = nullptr;
  if (true || d->val) {
    std::cout << "no error" << std::endl;
  }
  else {
    std::cout << "never executes" << std::endl;
  }

  return 0;
}

x = 5
y = x + 1
z = y^2 / x
result = floor(z)
x = 5
y = 5 + 1
z = (5 + 1)^2 / 5
result = floor((5 + 1)^2 / 5)
fn main() {
    let v = 1..1_000_000;
    let vs: Vec<_> = v.map(|x| x * 2 ).take(5).collect();
    println!("{:?}", vs);
}

Not covered:

  • cache hit optimization
  • polymorphism costs
  • concurrency
void quick_sort (int *a, int n) {
    int i, j, p, t;
    if (n < 2)
        return;
    p = a[n / 2];
    for (i = 0, j = n - 1;; i++, j--) {
        while (a[i] < p)
            i++;
        while (p < a[j])
            j--;
        if (i >= j)
            break;
        t = a[i];
        a[i] = a[j];
        a[j] = t;
    }
    quick_sort(a, i);
    quick_sort(a + i, n - i);
}
def quickSort(arr):
    less = []
    pivotList = []
    more = []
    if len(arr) <= 1:
        return arr
    else:
        pivot = arr[0]
        for i in arr:
            if i < pivot:
                less.append(i)
            elif i > pivot:
                more.append(i)
            else:
                pivotList.append(i)
        less = quickSort(less)
        more = quickSort(more)
        return less + pivotList + more
fn quick_sort<T>(v: &mut [T], f: &OrderFunc<T>) {
 
    let len = v.len();
    if len < 2 {
        return;
    }
 
    let pivot_index = partition(v, f);
 
    // Sort the left side
    quick_sort(&mut v[0..pivot_index], f);
 
    // Sort the right side
    quick_sort(&mut v[pivot_index + 1..len], f);
}
 
fn partition<T>(v: &mut [T], f: &OrderFunc<T>) -> usize {
    let len = v.len();
    let pivot_index = len / 2;
 
    v.swap(pivot_index, len - 1);
 
    let mut store_index = 0;
    for i in 0..len - 1 {
        if f(&v[i], &v[len - 1]) {
            v.swap(i, store_index);
            store_index += 1;
        }
    }
 
    v.swap(store_index, len - 1);
    store_index
}
qsort [] = []
qsort (x:xs) = qsort [y | y <- xs, y < x] ++ [x] ++ qsort [y | y <- xs, y >= x]
(defn qsort [[pivot & xs]]
  (when pivot
    (let [smaller #(< % pivot)]
      (lazy-cat (qsort (filter smaller xs))
		[pivot]
		(qsort (remove smaller xs))))))

Performance and Functional Programming

By Clint Liddick

Made with Slides.com

Performance and Functional Programming

  • 1,699

More from Clint Liddick