Bernardo Aceituno,
Carlos Mastalli,
Hongkai Dai,
Michele Focchi,
Andreea Radulescu,
Darwin G. Caldwell,
Jose Cappelletto,
Juan C. Grieco,
G. Fernandez-Lopez,
Claudio Semini
Centroidal Dynamic Model
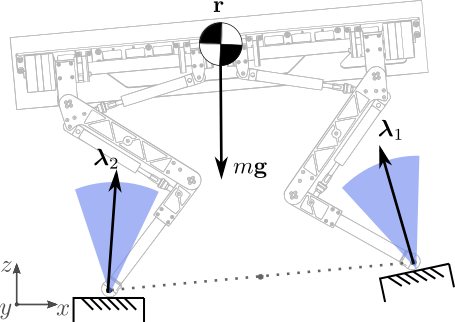
- Non-coplanar stability through friction cone constraints
- The centroidal dynamics describes the system's evolution
- Integer variables model the contacts and gait transitions
- Approximate the robot's joint torque limits
We represent the time evolution of the system using a centroidal dynamics model [1]
\begin{bmatrix}
m \ddot{\mathbf{r}} \\
\dot{\mathbf{k}}
\end{bmatrix} = \begin{bmatrix}
m \mathbf{g} + \sum_{l = 1}^{n_l} \mathbf{\lambda}_{l} \\
\sum_{l = 1}^{n_l} (\mathbf{p}_{l} - \mathbf{r}) \times \mathbf{\lambda}_{l}
\end{bmatrix}
where
- CoM position
- Angular Momentum
- Contact force of end-effector
- Position of end-effector
Centroidal Dynamic Model
\mathbf{r}
\mathbf{k}
\mathbf{\lambda}_l
\mathbf{p}_l
[1] Orin et al., "Centroidal dynamics of a humanoid robot", 2013
We represent the time evolution of the system using a centroidal dynamics model
\begin{bmatrix}
m \ddot{\mathbf{r}} \\
\dot{\mathbf{k}}
\end{bmatrix} = \begin{bmatrix}
m \mathbf{g} + \sum_{l = 1}^{n_l} \mathbf{\lambda}_{l} \\
\sum_{l = 1}^{n_l} (\mathbf{p}_{l} - \mathbf{r}) \times \mathbf{\lambda}_{l}
\end{bmatrix}
The non-linear term can be described as bilinear function [2], and it can be decomposed as:
Centroidal Dynamic Model
(\mathbf{p}_l - \mathbf{r}) \times \mathbf{\lambda}_l
\mathbf{ab} = \frac{\mathbf{u}^+ - \mathbf{u}^-}{4}
\mathbf{u}^+ \geq (\mathbf{a} + \mathbf{b})^2
\mathbf{u}^- \geq (\mathbf{a} - \mathbf{b})^2
[2] Ponton et al., "A Convex Model of Momentum Dynamics for Multi-Contact MotionGeneration", 2013
A gait matrix [3] describes when i contact swings in determined time-slot j :
Since each contact location in the plan is reached once, we enforce:
Contact and Gait Sequence
\sum_{j=1}^{N_t} \mathbf{T}_{i j} = 1 \ , \ \forall i = 1,..,N_f.
(\mathbf{T}_{ij} = 1)
N_f
N_t
\mathbf{T} \in \{0,1\}^{N_f\times N_t}
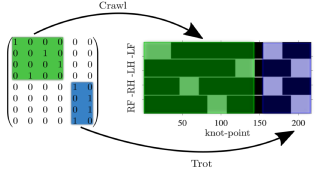
- Number of contacts
- Number of time-slots
[3] Aceituno-Cabezas et al., “A Mixed-Integer Convex Optimization Framework for Robust Multilegged
Robot Locomotion Planning over Challenging Terrain”, 2017
Once is assigned the contact to swing, we optimize the contact locations, represented as 4D vectors:
and then, we assign this contact to one of the by using a binary matrix :
Contact and Gait Sequence
\sum_{\mathrm{r} = 1}^{N_r}{\mathbf{H}_{i \mathrm{r}}} = 1, \mathbf{H}_{i
\mathrm{r}} \Rightarrow A_\mathrm{r} \mathbf{f}_i \leq b_r,
\mathbf{H} \in \{0,1\}^{N_f\times N_r}
\Rightarrow
N_r
\mathbf{f} = (f_x, f_y, f_z, \theta),
where the (implies) operator is represented with big-M formulation.
[3] Aceituno-Cabezas et al., “A Mixed-Integer Convex Optimization Framework for Robust Multilegged
Robot Locomotion Planning over Challenging Terrain”, 2017
We approximate the kinematic limits as a bounding box with respect to the CoM. Algebraically:
where
- CoM position at i transition
- Diagonal of the bounding box
- Distance from the trunk of leg
Contact and Gait Sequence
\mathbf{r}_{T(i)}
L_i
d_{\lim}
\left |
\mathbf{f}_{i} -
\left[
\mathbf{r}_{T(i)} +
L_i
\begin{pmatrix}
\cos(\theta_i + \phi_i) \\
\sin(\theta_i + \phi_i)
\end{pmatrix}
\right]
\right |
\leq d_{lim}
and the trigonometric functions are decomposed in piecewise linear
functions [4].
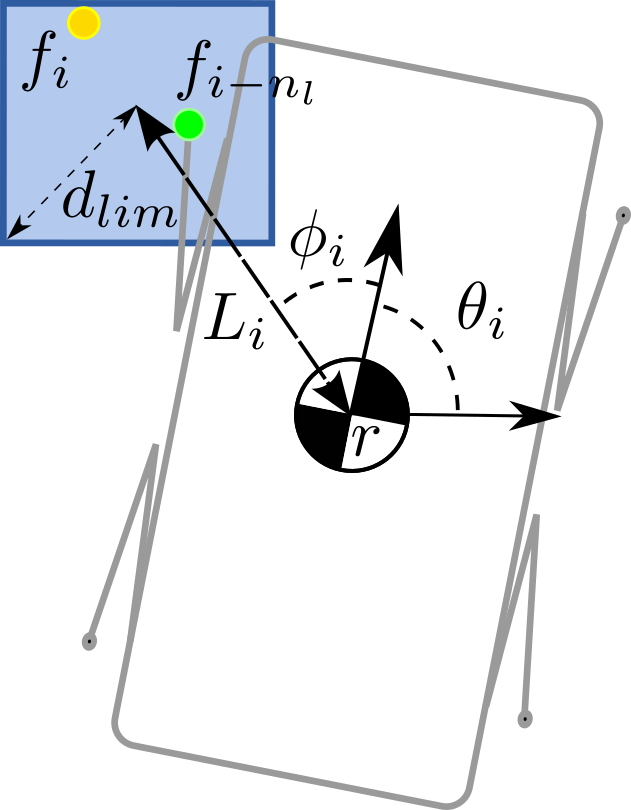
[4] Deits and Tedrake, “Footstep Planning on Uneven Terrain with Mixed-Integer Convex Optimization”, 2014
We define as swing reference trajectory, connected to adjacent
contacts, where:
- j indicates the time-slot, and
- all the knots per time-slot
Contact and Gait Sequence
t \in [1, \cdots, N_k]
\mathbf{T}_{ij} \Rightarrow \mathbf{p}_{l(i)\gamma(j,N_k)} = \mathbf{f}_i,
\mathbf{f}_i
This constraint enforces that the leg reaches the contact position at
the end of the j slot
\gamma(j,t)
with:
The leg number for the i contact
l(i)
For stance condition, we constraint the leg to remain stationary as:
- are the contact indexes assigned to the l leg
Contact and Gait Sequence
\forall t \in [2,\cdots,N_k],
\sum_{i \in C(l)}^{ } \mathbf{T}_{i j} = 0 \Rightarrow \mathbf{p}_{l \gamma(j,t)} =
\mathbf{p}_{l \gamma(j,1)}
where
C(l)
If a swing is activated on l leg, there is no contact force:
Contact and Gait Sequence
NC(j)
\sum_{i \in C(l)}\mathbf{T}_{i j} = 1 \Rightarrow \mathbf{\lambda}_{l \gamma(j,t)} = 0 \ , \ \forall t \in NC(j),
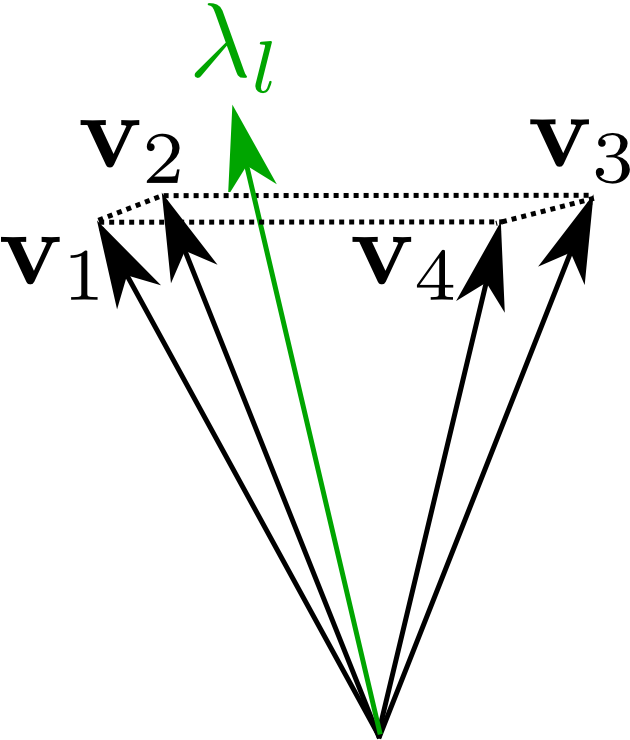
where is the set of knots in the j slot used for the swing.
This can be see as complementary constraint [5,6]
[5] Stewart and Trinkle, “An implicit time-stepping scheme for rigid body dynamics with Coulomb friction”, 2000
[6] Mastalli et al., “Hierarchical Planning of Dynamic Movements without Scheduled Contact Sequences”, 2016
We add robustness to this condition because we maximize a lower bound of the distance of the force vector to each cone edge as:
Contact and Gait Sequence
\rho_e
(\alpha)
where are positive multipliers on each cone edge
We can ensure stability on arbitrary terrain with non-coplanar contacts by incorporating linearized friction cone constraints:
\mathbf{\lambda}_{l j} \in \mathbb{FC}_\mathrm{r} \Rightarrow
\mathbf{\lambda}_{l j} = \sum_{e = 1}^{N_e} \rho_e \mathbf{v}_{\mathrm{r}_e} \ , \ \rho_1, \cdots,
\rho_{N_e} > 0,
\alpha = \text{arg}\max_{\bar{\alpha}}\text{ s.t }\mathbf{\lambda}_{l j} -
\bar{\alpha} \hat{\mathbf{n}}_\mathrm{r} \in \mathbb{FC}_\mathrm{r}.
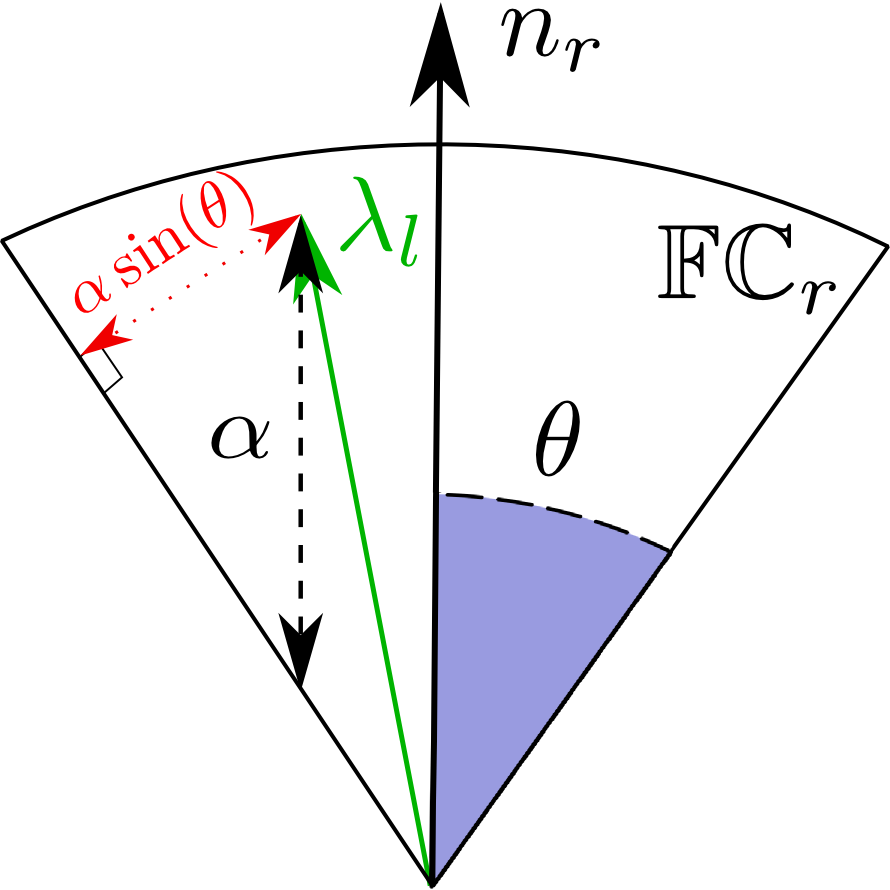
Contact and Gait Sequence
We approximate joint torque limits by using a nominal value of the Jacobian :
\mathbf{J}_{l,j}^*
{\mathbf{J}^*}_{l,j}^{T} \mathbf{\lambda}_{l,j} \leq \mathbf{\tau}_{max},
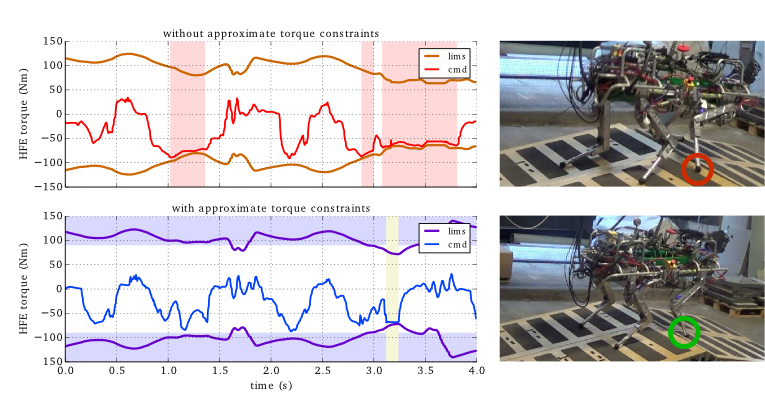
HyQ Crossing Terrain with Various Slopes
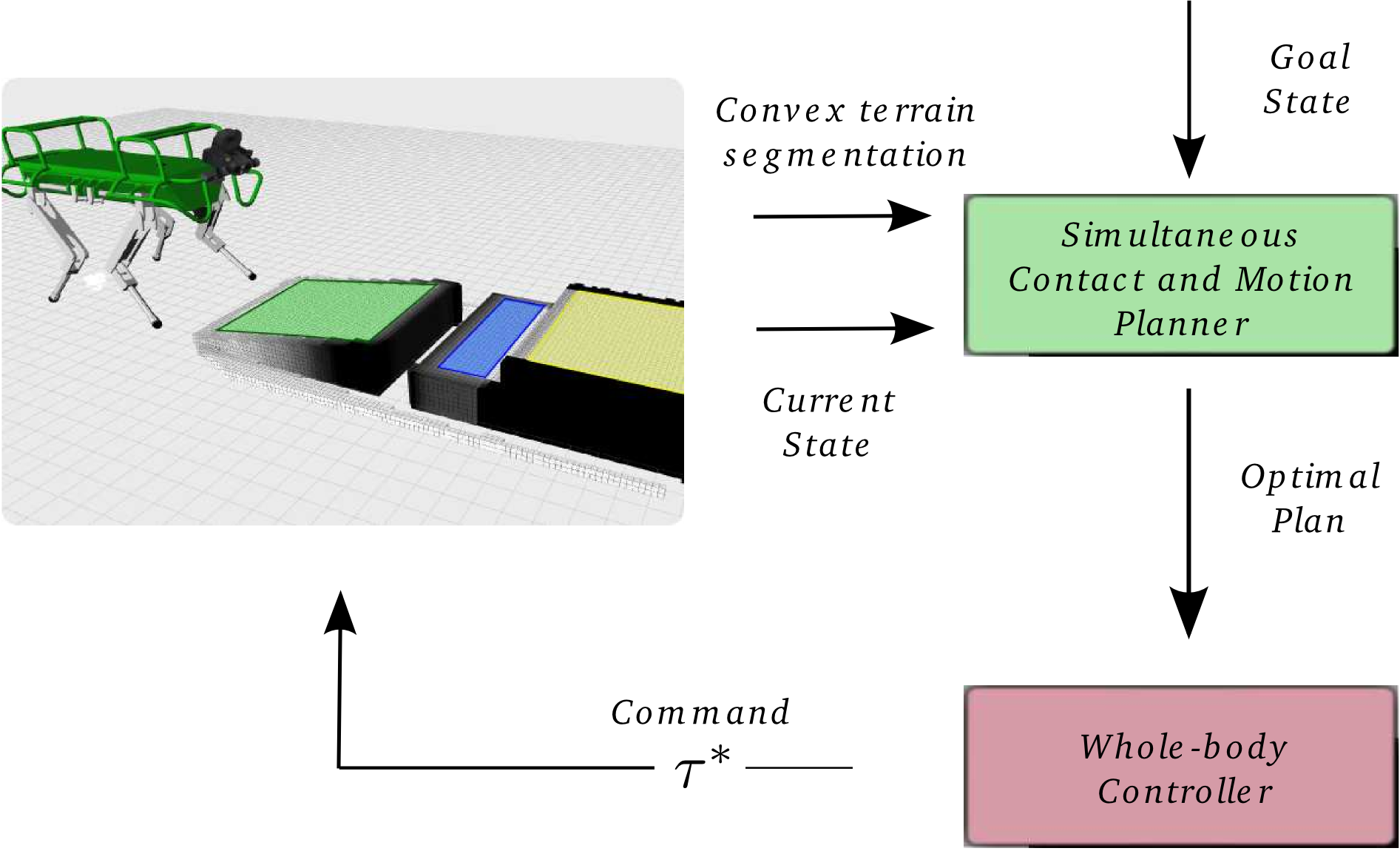
Simultaneous Contact, Gait and Motion Planning for Robust Multi-Legged Locomotion via Mixed-Integer Convex Optimization
By Carlos Mastalli
Simultaneous Contact, Gait and Motion Planning for Robust Multi-Legged Locomotion via Mixed-Integer Convex Optimization
Simultaneous Contact, Gait and Motion Planning for Robust Multi-Legged Locomotion via Mixed-Integer Convex Optimization (RAL)
