計算幾何

Computational Geometry

高雄中學洪駿輝

codingbeans

Q&A

Q:計算幾何？IOI不是不考嗎？

Q:我根本就沒練過任何計算幾何題，我該睡了嗎？

Q:話說你哪來的啊？聽都沒聽說過！

A:的確不考，但是TOI模考是會考的。還有ACM。

A:不用擔心，會從最基本的開始說起。

A:我是雄中的洪駿輝，確實是沒名氣的弱者QQ。

二維幾何基礎

有點無聊

點

struct Point
{
    double x,y;
};

就這樣:)

向量

struct Vector
{
    double x,y;
};

struct Point
{
    double x,y;
};
typedef Point Vector;

:)

位移量

一些運算

struct Point
{
    double x,y;
    Point(double x=0,double y=0):x(x),y(y) {}
};

typedef Point Vector;

// Vector + Vector = Vector
Vector operator + (Vector A,Vector B) {return Vector(A.x+B.x,A.y+B.y);}
// Point - Point = Vector
Vector operator - (Point A,Point B) {return Vector(A.x-B.x,A.y-B.y);}
// Vector * num = Vector
Vector operator * (Vector A,double t) {return Vector(A.x*t,A.y*t);}
// Vector / num = Vector
Vector operator / (Vector A,double t) {return Vector(A.x/t,A.y/t);}

內積(Dot)

double Dot(Vector A,Vector B) {return A.x * B.x + A.y * B.y;}

\vec{a}\cdot \vec{b}

\vec{a}\cdot \vec{b}

=a_{x}\ast b_{x} + a_{y}\ast b_{y}

=a_{x}\ast b_{x} + a_{y}\ast b_{y}

= \left | \vec{a}\right | \ast \left | \vec{b}\right | \cos \theta

= \left | \vec{a}\right | \ast \left | \vec{b}\right | \cos \theta

double Length(Vector A) {return sqrt(Dot(A,A));} // sqrt(A.x*A.x + A.y*A.y)

double getangle(Vector A,Vector B) {return acos( Dot(A,B)/Length(A)/Length(B) );}

外積(Cross)

\vec{a}\times \vec{b}

\vec{a}\times \vec{b}

= \left | \vec{a}\right | \times \left | \vec{b}\right | \sin \theta

= \left | \vec{a}\right | \times \left | \vec{b}\right | \sin \theta

一個同時垂直於a,b的向量，顯然平行z軸

可是這是二維幾何耶T_T

大小

= a_{x}\ast b_{y} - a_{y}\ast b_{x}

= a_{x}\ast b_{y} - a_{y}\ast b_{x}

double Cross(Vector A,Vector B) {return A.x*B.y - A.y*B.x;}

double Area(Point A,Point B,Point C) {return Cross(B-A,C-A) / 2.0;}

注意：有向面積

向量位置關係

(0,+)

(-,+)

(-,-)

(0,-)

(+,-)

(+,0)

(+,+)

(-,0)

(內積,外積)

超

級

重

要

線

表示法

```
兩點式
```

參數式

P+t\ast \vec{v}

P+t\ast \vec{v}

```
點和向量決定唯一直線
```

struct Line
{
    Point p;
    Vector v;
    double ang;
    Line(Point p,Vector v):p(p),v(v) {ang=atan2(v.y,v.x);}
};

t \in \mathbb{R} \Rightarrow Line

t \in \mathbb{R} \Rightarrow Line

t \in \left [ 0,\infty \right ] \Rightarrow Ray

t \in \left [ 0,\infty \right ] \Rightarrow Ray

t \in \left [0,1 \right ] \Rightarrow Segment

t \in \left [0,1 \right ] \Rightarrow Segment

一些問題

解直線交點

點到直線距離，點到線段距離

求點到直線上投影點

判定兩線段是否香蕉相交

思路：設想求出直線上的某點

A = P + t \ast \vec{v}

A = P + t \ast \vec{v}

列方程，真的將算出

t

配合內外積正確判斷點的位置

code省略：）

面

多邊形

typedef vector<Point> Polygon;

將頂點按照順序存下（通常是逆時針）

圓心和半徑

struct Circle
{
    Point c;
    double r;
    Circle(Point c,double r=0):c(c),r(r) {}
};

多邊形的問題

求多邊形面積

測量師公式：

\frac{1}{2}\sum_{i=0}^{n} \left | \vec{p}_{i} \times \vec{p}_{(i+1)\%n} \right |

\frac{1}{2}\sum_{i=0}^{n} \left | \vec{p}_{i} \times \vec{p}_{(i+1)\%n} \right |

凸包

判斷點是否在簡單多邊形內

大量詢問點是否在凸多邊形內

旋轉卡尺

圓的一些問題

都很煩

求圓和直線交點

求圓和圓交點

求過某點做圓的切線

求兩圓公切線

思路：不外乎

1.硬解x,y聯立方程

2.硬解參數t

3.算長度，算圓上極角，求得點

大

補

帖

UVa 12304

二維常見算法

點在多邊形內判定

射線法

從給定點往右引一條無限遠的射線，若與多邊形相交奇數次則在多邊形內部，偶數次則否。

轉角法

多邊形相對於給定點轉了幾度

內部 , 外部 , 邊上

360^{\circ}

360^{\circ}

0^{\circ}

0^{\circ}

180^{\circ}

180^{\circ}

轉角法變形 --- 繞數法

bool isPointOnSegment(Point P,Point A,Point B)
{
    return Cross(P-A,P-B) == 0 && Dot(P-A,P-B) <= 0;
}
typedef vector<Point> Polygon;
int IsPointInPolygon(Point p,Polygon poly)
{
    int n= poly.size();
    int wn=0;
    for(int i=0;i<n;i++)
    {
        if(isPointOnSegment(p,poly[i],poly[(i+1)%n])) return -1; // 邊上
        int k = Cross( poly[(i+1)%n] - poly[i] , p - poly[i]);
        int d1 = poly[i].y - p.y;
        int d2 = poly[(i+1)%n].y - p.y;
        if(k > 0 && d1<=0 && d2>0) wn++; //逆時針穿過，繞數+1
        if(k < 0 && d1>0 && d2<=0) wn--; //順時針穿過，繞數-1
    }
    return wn!=0;
}

可以盯著code，畫張圖，感受一下他與轉角法的關聯:)

大量詢問點是否在凸多邊形內

題目敘述：給一個有n<=100000個點的凸多邊形，以及q<=100000個詢問，每次詢問給出一個點p，請判斷他是否位於凸多邊形內。

暴力： QQ沒救

O(nq)

O(nq)

其實可以做到預處理，查詢。

O(n)

O(n)

O(\log n)

O(\log n)

考慮多邊形內部一點C，所有頂點相對於C便形成了一類極角排序，並將切割成了N個角度區間。

360^\circ

360^\circ

可以二分搜出詢問點P位於哪個區間，然後判線段相交就好了！

凸包

題目敘述：給定平面上N個點，求一面積最小的凸多邊形使得所有點都在此凸多邊形當中。

暴力法：

枚舉條線段，每條線段花判斷是否在凸包上(即是否所有點都在此線段同一側)，時間複雜度

O(n^{2})

O(n^{2})

O(n)

O(n)

O(n^{3})

O(n^{3})

有點慢耶QQ 能不能只掃描過一次點集就出解呢？

可以！

不過掃描法需要有序的進行，在二維幾何中一個好的順序應該是......？

極角觀點：Graham's scan

1. 找到y值最小的點，若有多個，選擇x值最小的點。設此點為P

2. 將所有點依照對P的極角排序。

3. 依照極角序加入點。

構成左轉時，直接加入點至末端。

當發現需要右轉時，不斷彈出末端的

點直到構成左轉。

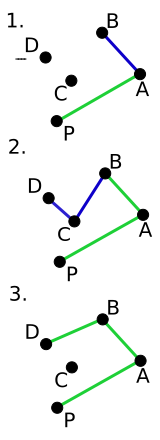
時間複雜度：

O(n\log n)

O(n\log n)

水平序觀點：Andrew算法

1. 將所有點按照x的座標大小排序，若x相同則依y的大小排序。

2. 和Graham算法類似。依照順序加入點，若構成右轉則不斷彈

出末端的點直到形成左轉。

3. 第2步完畢時，已有下凸包。將下凸包最右的點作為起點，反

向進行步驟2，即可得到上凸包。合併即是所求凸包。

時間複雜度：

O(n\log n)

O(n\log n)

struct Point
{
    double x,y;
    Point(double x=0,double y=0):x(x),y(y) {}
    bool operator < (const Point& rhs) const {return x<rhs.x || (x==rhs.x && y<rhs.y);}
};

// Andrew
// 回傳凸包頂點數量
int ConvexHull(Point* p,int n,Point* ch)
{
    sort(p,p+n);
    int m=0;
    // 下凸包
    for(int i=0;i<n;i++)
    {
        while(m > 1 && Cross(ch[m-1]-ch[m-2],p[i]-ch[m-2]) <=0 ) m--;
        ch[m++]=p[i];
    }
    int k=m;
    // 上凸包
    for(int i=n-2;i>=0;i--)
    {
        while(m > k && Cross(ch[m-1]-ch[m-2],p[i]-ch[m-2]) <=0 ) m--;
        ch[m++]=p[i];
    }
    // 注意p[0]會重複選到
    if(n>1) m--;
    return m;
}

旋轉卡尺

題目敘述：平面上n 個點，求任兩點間距離的最大值。

暴力：

O(n^{2})

O(n^{2})

小觀察：解一定發生在凸包的點對上，所以先求凸包減少許多無用點後，再暴力！

O(n^{2})

O(n^{2})

旋轉卡尺是一對完全夾住凸包且不斷旋轉的直線

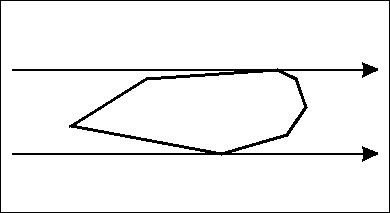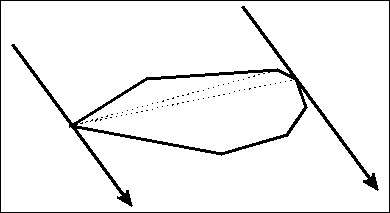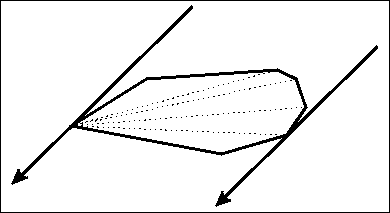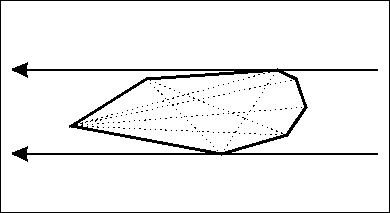
旋轉的過程中會取到一個最遠距離（長）與最近距離（寬）

\leq10^{5}

\leq10^{5}

設兩條卡尺通過的點為與 , ，則他們稱作一對對踵點對。那麼只要找出所有對踵點對當中最長的距離即為所求。

P_{i}

P_{i}

P_{j}

P_{j}

1. 任一時間最多只有4對對踵點對

一些性質：

2. 只需考慮一條卡尺貼邊的情況，計算出另一條卡尺的位置並更新答案即可。

↑可以先自己想一下為什麼XD

一般將貼著邊旋轉的稱為主卡尺，另一條卡住一個點的稱為副卡尺

double Rotating_Calipers(Point* p,int n)
{
    if(n<=1) return 0;
    if(n==2) return dist(p[0],p[1]);
    double ans=0;
    
    for(int i=0,j=2;i<n;i++)
    {
        // 若穿過p[j+1]比穿過p[j]要離主卡尺更遠則j<-j+1，實作上直接用外積判斷
        while(Cross(p[(i+1)%n]-p[i],p[(j+1)%n]-p[i])
                > Cross(p[(i+1)%n]-p[i],p[j]-p[i])) j=(j+1)%n;
        ans = max(ans,dist(p[i],p[j]));
        ans = max(ans,dist(p[(i+1)%n],p[j]));
    }
    return ans;
}

例題：給一個n<=100000個點的凸多邊形，求包住此凸多邊形的最小矩形面積

想法不難，可以想想看:)

半平面交

何謂半平面？

定義有向直線的左邊就是他所對應的半平面

半平面交指的就是這些半平面的交集

題目敘述：給出n<=100000個半平面，求出他們所交出的凸多邊形（也可能是無界多邊形，或退化成線，點，空集合）

暴力(增量)法：依次加入半平面，並維護目前得到的凸多邊形。即算出當前有向直線與凸多邊形的交點，保留或捨棄某些點得到新的凸多邊形。

O(n^{2})

O(n^{2})

當然，這樣並不夠好:)

跟凸包的Graham算法類似，我們考慮按照極角序來依次加入半平面。

接下來的事情就和凸包幾乎一樣了：

檢查原本的半平面是否會因為即將進入的半平面而失效
加入此半平面

不同的是，凸包用的是stack，半平面交用的是deque

struct Line
{
    Point p;
    Vector v;
    double ang;
    Line(Point p=0,Vector v=0):p(p),v(v) {ang=atan2(v.y,v.x);}
    bool operator < (const Line& rhs) const {return ang < rhs.ang;}
};
// P 是否在有向直線 L 的左邊
inline bool OnLeft(Point P,Line L)
{
    return Cross(L.v,P-L.p) > 0;
}
// 回傳兩直線交點
Point GetLineIntersec(Line L1,Line L2)
{
    double t = Cross(L2.p-L1.p,L2.v) / Cross(L1.v,L2.v);
    return L1.p + L1.v*t;
}

// 回傳凸多邊形點數
int HalfPlaneIntersec(Line* L,int n,Point* poly)
{
    sort(L,L+n);

    int first=0,last=0; // deque 的指針
    Point* p = new Point[n];
    Line* q = new Line[n];
    q[last++]=L[0];
    for(int i=1;i<n;i++)
    {
        while(last-first>=2 && !OnLeft(p[last-2],L[i])) last--;
        while(last-first>=2 && !OnLeft(p[first],L[i])) first++;
        if(Cross(L[i].v,q[last-1].v)==0) // 有向直線平行，取內側的直線
        {
            if(OnLeft(L[i].p,q[last-1])) q[last]=L[i];
        }
        else q[last++]=L[i];
        if(last-first>=2) p[last-2] = GetLineIntersec(q[last-1],q[last-2]);
    }
    while(last-first>=2 && !OnLeft(p[last-2],q[first])) last--;
    if(last-first<3) return 0; // 無界多邊形
    p[last-1]=GetLineIntersec(q[first],q[last-1]);

    int m=0;
    for(int i=first;i<last;i++) poly[m++]=p[i];
    delete[] p;delete[] q;
    return m;
}

掃描線專題

前面曾經提過，在二維幾何中常用的兩種序是水平序和極角序，他們在掃描線的題目中佔有重要的地位。

例題(UVa 1606)：平面上有n<=1000個點，每個點為黑色或白色。現在要放置一個隔板，求隔板一端的白點數量加上另一端的黑點數量的最大值。(隔板上的點視為同時在兩端)

暴力：枚舉條直線，再花計算答案

O(n^{2})

O(n^{2})

O(n)

O(n)

O(n^{3})

O(n^{3})

考慮枚舉參考點P，按照極角序掃描每一個點，動態維護直線兩端的黑白點數量。

枚舉個參考點，每次掃描花費

O(n)

O(n)

O(n\log n)

O(n\log n)

O(n^{2}\log n)

O(n^{2}\log n)

例題(已往生的HOJ 12)：給定平面上n<=50000個矩形，求他們的聯集面積。

考慮一條依照水平序從左到右進行的掃描線

將每個矩形拆成兩個事件(event):

1. 進：掃描線通過矩形左界

2. 出：掃描線通過矩形右界

在事件與事件之間，矩形覆蓋到的y座標區間不變沒有矩形進入或出去。直接計算覆蓋面積。

\because

\because

需要支持對y座標區間 1，還有查詢不為0的y區間總和？

\pm

\pm

線段樹！

O(n\log n)

O(n\log n)

例題：給你n<=100000條線段，請判斷是否存在任何兩條線段相交？

沿用上題思想，考慮從左到右進行的掃描線

兩種事件：

1. 線段左端點(進)

2. 線段右端點(出)

考慮以平衡樹維護線段的左端點y座標順序

只須在線段出平衡樹時檢查一下該線段與平衡樹中前後鄰居是否相交即可。

正確性需要分幾種case證明，這裡略去:)

例題選講

練習！練習出真知！只有練習才能夠有全面的感受！

(7/29交大練習賽)(ACM/ICPC Japan 2009)
題目敘述：平面上有n<=500個黑點與m<=500個白點，請判斷是否存在一條直線使得任取一個黑點或白點都在直線的異側？

觀察：存在一直線完全分離黑點與白點若且惟若黑點的凸包與白點的凸包的交為空

求出黑點與白點的凸包。
枚舉黑凸包上的所有邊檢查是否與白凸包相交。

AC

O(n^{2})

O(n^{2})

特殊情況：黑凸包被白凸包完全包含。只要任取一個黑點判斷是否在白凸包內即可，記得也要判白點在不在黑凸包內。

WA

(NTUJ 2577)
題目敘述：給定兩個凸多邊形，分別有n<=100,m<=100個點，求出他們的交集面積，最多有tc<=100個testcase。

注意到可以將凸多邊形視為半平面交的結果。
那麼兩個凸多邊形的交集其實就是所有半平面的交集。

拆解出n+m個半平面，做出半平面交後求凸多邊形面積即為所求

O(tc(n+m)\log(n+m))

O(tc(n+m)\log(n+m))

AC

(Codeforces 536C)
題目敘述：
有n<=100000個運動員參加運動比賽，這場比賽有兩個項目：游泳R公尺和賽跑S公尺。選手在完成一項後會立即開始下一項
你知道這n個運動員各自在這兩個項目的速度：第i個人每秒游r_i公尺，跑s_i公尺。但是你不知道R,S分別是多少，只知道他們是正實數。
試問有哪些人可能獲得冠軍？(即兩個項目時間總和最少的人)

第一步有點跳躍：將每個人對應到座標上的點

(\frac{1}{r_{i}} ,\frac{1}{s_{i}})

(\frac{1}{r_{i}} ,\frac{1}{s_{i}})

每位選手的秒數其實就是將點代入

R\ast x + S\ast y

R\ast x + S\ast y

記得線性規劃嗎？

R\ast x + S\ast y , R>=0 , S>=0

R\ast x + S\ast y , R>=0 , S>=0

斜率為負的這條直線在點集當中能取到的最小值發生在凸包的左下方

套凸包算法，計算左下方的凸包點數。

O(n\log n)

O(n\log n)

AC

(UVa1298)

題目敘述：有n<=100個運動員，他們參加一個有三個項目的比賽：游泳V公尺，騎自行車U公尺，和賽跑W公尺。選手在完成一項後會立即開始下一項。
你知道他們每個人各自在這三個項目的速度：第i個人每秒游v_i公尺，騎u_i公尺，跑w_i公尺。但是你不知道這三個項目各自的長度。
請求出有哪些人可能奪冠。(三項時間總和最短)

如果沿用上一題的思考，我們會需要做三維凸包，然後去思考有哪些面可以跟形如的面相切

V\ast x + U\ast y + W\ast z = C

V\ast x + U\ast y + W\ast z = C

的確並非不能做，但是至少我不會做QQ

注意到這題的n<=100，這給予我們去枚舉任意兩個人並檢查他們勝負條件的空間。

方便起見設比賽總長1公尺：游泳V公尺，自行車U公尺，賽跑1-V-U公尺。(這樣做是合理的，因為只有比例重要)
考慮第i個人與第j個人。第i個人要贏第j個人的條件是

\frac{V}{v_{i}} + \frac{U}{u_{i}} + \frac{1-V-U}{w_{i}} < \frac{V}{v_{j}} + \frac{U}{u_{j}} + \frac{1-V-U}{w_{j}}

\frac{V}{v_{i}} + \frac{U}{u_{i}} + \frac{1-V-U}{w_{i}} < \frac{V}{v_{j}} + \frac{U}{u_{j}} + \frac{1-V-U}{w_{j}}

這是一個二元一次的不等式。可整理成

ax + by + c > 0

ax + by + c > 0

這對應一個半平面

如此，對於每個選手i，枚舉所有其他選手，會得到n個半平面。有奪冠機會若且惟若半平面交有解。

O(n) \ast O(n\log n) = O(n^{2}\log n)

O(n) \ast O(n\log n) = O(n^{2}\log n)

AC

(NTUJ 2605)(ACM/ICPC NWERC 2014) TimeLimits: 9 s

題目敘述：給定平面上n<=100000個點，請判斷是否有一條直線至少通過p%的點(20<=p<=100)，即至少通過[n*p/100]個點（上高斯）。

極角掃描？

O(n^{2}\log n)

O(n^{2}\log n)

似乎沒什麼好方法QQ

注意p>=20是個有趣的範圍，說明了至少這條線要通過1/5的點

那麼任取兩個點，剛好選中答案的那條直線的機率大概是 1/25

所以隨機選兩個點，判斷此直線是否滿足要求。做個7122次之後還是沒找到可直接斷定無解。

O(n)

O(n)

AC

O(7122n)

穿越次元之壁

三維幾何

三維凸包

暴力法：

O(n^{4})

O(n^{4})

能不能藉著掃描的思想加速呢？

話說，三維幾何內一個好的順序是......

？？

目前沒有人知道QAQ

實踐中常用：

卷包裹法

增量法

雖然沒有好用的順序，還是可以把點一個一個加進來然後維護好當前凸包。

O(n^{2})

O(n^{2})

其實可以用Divide and Conquer 做到

O(n\log n)

O(n\log n)

小結

對基礎問題的大量熟練度

對圖形與圖形關係的想像力

沒有講到的東西：

誤差分析 -- eps

三分搜尋法，爬山法，梯度下降法，模擬退火法

數值方法：

隨機增量法：最小包含圓問題

計算幾何的難題？

結合圖論算法 e.g. PSLG

幾何只是輔助，其實要考(資結/數論)

複雜的數學分析與建模

參考資料&圖片來源

```
半平面交算法及简单应用
```

http://www.cnblogs.com/huangxf/p/4067763.html

Graham's scan -- Wikipedia

https://en.wikipedia.org/wiki/Graham_scan

旋转卡壳算法 - ACM算法

http://www.alphaway.org/post-93.html

模板code來源：算法競賽入門經典訓練指南 -- 劉汝佳

2015程式解題競賽集訓營講義

Computational Geometry

By codingbeans

Computational Geometry

Lecture.

計算幾何

Computational Geometry

Q&A

Q:計算幾何？IOI不是不考嗎？

Q:我根本就沒練過任何計算幾何題，我該睡了嗎？

Q:話說你哪來的啊？聽都沒聽說過！

A:的確不考，但是TOI模考是會考的。還有ACM。

A:不用擔心，會從最基本的開始說起。

A:我是雄中的洪駿輝，確實是沒名氣的弱者QQ。

目錄

二維幾何基礎

常見二維算法

例題選講

穿越次元之壁

小結

二維幾何基礎

有點無聊

點

就這樣:)

向量

:)

位移量

一些運算

內積(Dot)

外積(Cross)

大小

向量位置關係

(0,+)

(-,+)

(-,-)

(0,-)

(+,-)

(+,0)

(+,+)

(-,0)

(內積,外積)

超

級

重

要

線

表示法

一些問題

解直線交點

點到直線距離，點到線段距離

求點到直線上投影點

判定兩線段是否香蕉相交

思路：設想求出直線上的某點

列方程，真的將 算出

配合內外積正確判斷點的位置

面

多邊形

將頂點按照順序存下（通常是逆時針）

圓

圓心和半徑

多邊形的問題

求多邊形面積

凸包

判斷點是否在簡單多邊形內

大量詢問點是否在凸多邊形內

旋轉卡尺

圓的一些問題

求圓和直線交點

求圓和圓交點

求過某點做圓的切線

求兩圓公切線

大

補

帖

UVa 12304

二維常見算法

點在多邊形內判定

射線法

轉角法

轉角法變形 --- 繞數法

可以盯著code，畫張圖，感受一下他與轉角法的關聯:)

大量詢問點是否在凸多邊形內

凸包

可以！

極角觀點：Graham's scan

列方程，真的將算出