How does the cosmic web impact galaxy formation?

Corentin Cadiou — PhD student

In collaboration with Marcello Musso, Yohan Dubois, Christophe Pichon

(Quick) Introduction

A very biased view on galaxy formation

Galaxy properties

\sim R_\mathrm{vir}
∼Rvir\sim R_\mathrm{vir}

Bulge

\underbrace{\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad}_{M_\star}
⎵M⋆\underbrace{\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad}_{M_\star}

Red or blue?

\frac{v_\mathrm{rot}}{\sigma}
vrotσ\frac{v_\mathrm{rot}}{\sigma}

Disk

   

All the properties vary with cosmic time…

Do they vary with spatial location?

 

Galaxies & the cosmic web

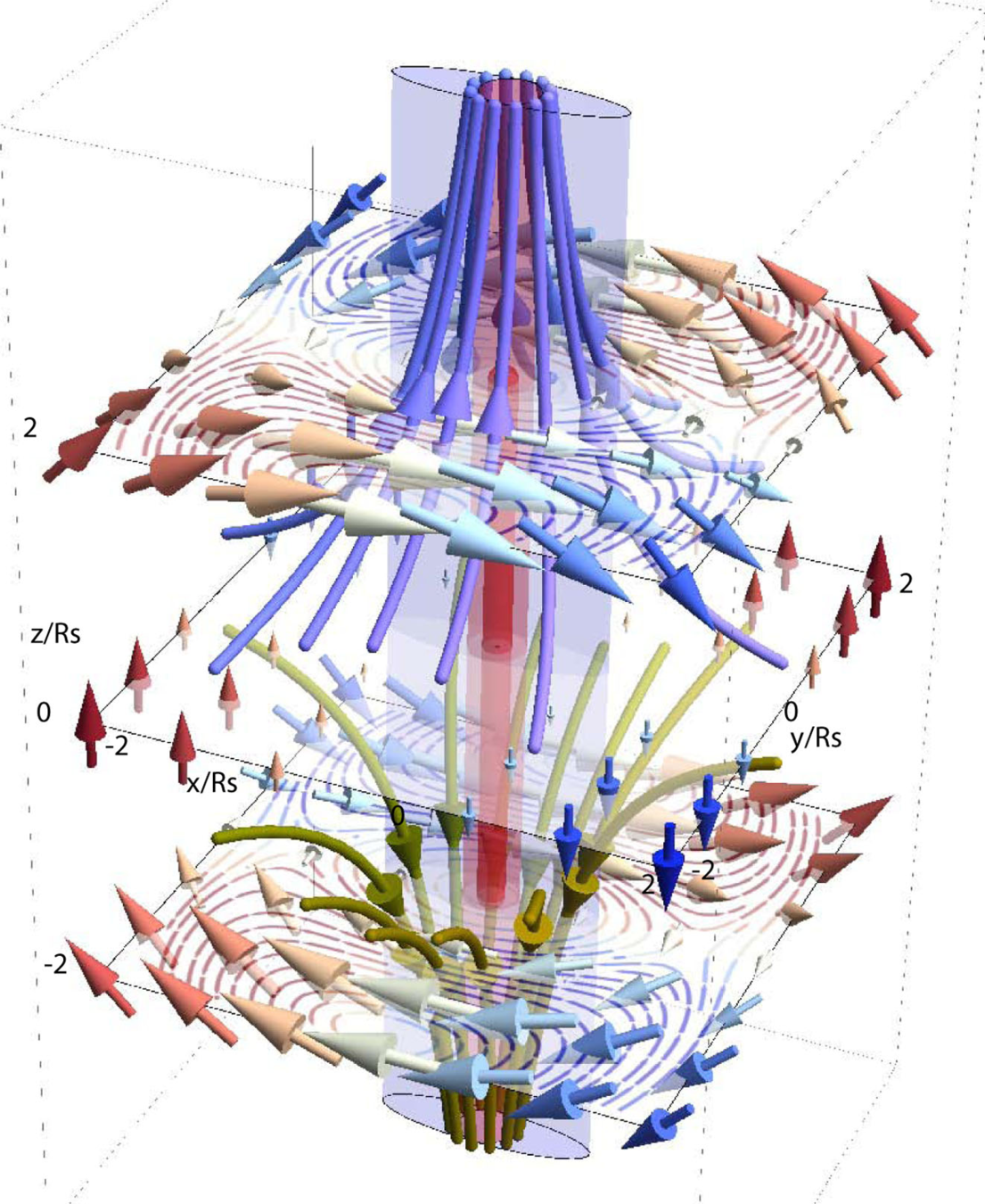
Halo model: galaxy properties are inherited from their parent halo + local density (~no effect of the cosmic web)

  • Kaiser bias: large scale overdensities bias halo density


    (Kaiser 84, BBKS 86)
     
  • Spins align with the cosmic web
    (Tempel&Libeskind 13, Codis+15, Chisari+15, ...)
     
  • Galaxy properties are modulated by the cosmic web
    (Laigle+17, Kraljic+18, Musso, Cadiou+18)
n_\mathrm{halo} = b n_\mathrm{DM}
nhalo=bnDMn_\mathrm{halo} = b n_\mathrm{DM}

We have to take into account the spatial modulation induced by the cosmic web

 

How do galactic and DM halo scales couple to the large scale anisotropies of the cosmic web?

The Excursion Set Theory

Excursion Set Theory

Galaxy properties & evolution from initial conditions
⇒ Find largest mass that will collapse by z at given location

Simulation Theory
M R
z
\delta
δ\delta

Spherical collapse model:

Structure of size R will collapse at z iff

\left\{\begin{matrix}\delta(R) =& \delta_c/D(z) \\ M(R)=&\frac{4\pi}{3}\bar\rho R^3 \end{matrix} \right.
{δ(R)=δc/D(z)M(R)=4π3ρˉR3\left\{\begin{matrix}\delta(R) =& \delta_c/D(z) \\ M(R)=&\frac{4\pi}{3}\bar\rho R^3 \end{matrix} \right.
\delta_c = 1.68 \text{, } D(z) \text{ is the linear growth factor}
δc=1.68, D(z) is the linear growth factor\delta_c = 1.68 \text{, } D(z) \text{ is the linear growth factor}

R

Excursion Set Theory

Galaxy properties & evolution from initial conditions
⇒ Find largest mass that will collapse by z at given location

Large mass                    Small mass

Early collapse

Late collapse

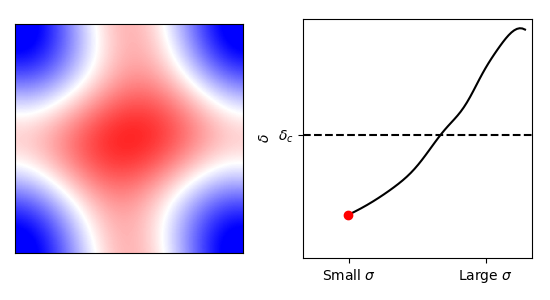
Constrained Excursion Set Theory

+

``How does the cosmic web biases the excursion and halo properties?´´

\delta(R) \Rightarrow \delta(R|\vec{r},\mathcal{S}) \quad \sigma(R) \Rightarrow \sigma(R|\vec{r}, \mathcal{S})
δ(R)⇒δ(R∣r⃗,S)σ(R)⇒σ(R∣r⃗,S)\delta(R) \Rightarrow \delta(R|\vec{r},\mathcal{S}) \quad \sigma(R) \Rightarrow \sigma(R|\vec{r}, \mathcal{S})

The Cosmic Web

How to encode the cosmic web?

Nodes (maxima of density)

Saddle point (center of filament)

Compressing the spatial information

1

2

3

Describe the critical points only

Compressing the spatial information

q_{ij} \equiv \nabla_i \nabla_j \varphi
qij≡∇i∇jφq_{ij} \equiv \nabla_i \nabla_j \varphi
\delta_{\mathcal{S}}
δS\delta_{\mathcal{S}}

Height: determined by (over-)density

Curvature: controlled by (traceless) tidal tensor

\bar{q}_{ij} \equiv q_{ij} - \delta_{ij}\frac{\mathrm{Tr}(q_{ij})}{3}
qˉij≡qij−δijTr(qij)3\bar{q}_{ij} \equiv q_{ij} - \delta_{ij}\frac{\mathrm{Tr}(q_{ij})}{3}

Poisson equation

\mathrm{Tr}(q_{ij}) \propto \delta_\mathcal{S}
Tr(qij)∝δS\mathrm{Tr}(q_{ij}) \propto \delta_\mathcal{S}

Results

Results

Direction of void

Direction of filament

In filaments, halos are...

  1. more massive
  2. form later (at fixed mass)
  3. accrete more (at fixed mass)

... than in voids

(Musso, Cadiou et al 2018)

(Kraljic+2018)

Results

The relevant parameter for quantifying the anisotropy is:

\mathcal{Q} \equiv \frac{r_i\bar{q}_{ij}r_j}{r^2}
Q≡riqˉijrjr2\mathcal{Q} \equiv \frac{r_i\bar{q}_{ij}r_j}{r^2}

Observation (in simu)

v/σ residuals at fixed dens + mass

Theory

But... why?

The filament constrains

  • the density                           
  • the variance of the density

Void         Filament          Void

Conclusion

Conclusions...

  • New model built, room for lots of improvement              
  • Classical results recovered
  • Help to uncover new results


...and perspectives

Towards a more comprehensive halo model

  • How do galaxy respond to large-scale anisotropies?
    ⇒ simulations (WIP)
  • Take into account non spherical collapse (WIP)
  • More subtle quantities:
    • halo merger rate (WIP)
    • halo concentration
    • ... star formation rate?

Thank you

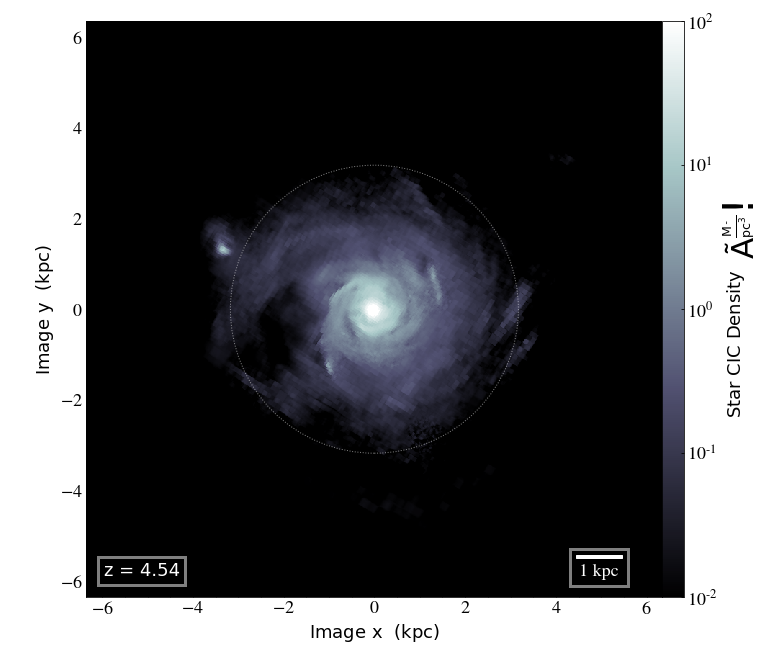
New Horizon simulation, Dubois+ in prep

Backup Slides

Excursion set at fixed final mass in different environments

Excursion set at fixed final mass in different environments

Effect of AGN feedback

The Formation of Disk Galaxy

! WIP !

Simulation Setup

  • suite of zoom-in simulations (~3-5), RAMSES (Teyssier 2002)
  • Δx = 35pc, Mstar = 1.1 10⁴ M☉ Mhalo=10¹² M☉
  • Turbulent star formation (Kimm+17, Trebitsch+17)
  • Mechanical feedback (Kimm+15)
  • AGN formation with spin-regulated efficiency (Dubois+12,+14)
  • 30,000,000 tracer particles (~10/cell, 0.5/star)*

*See Cadiou+18

Gas density

Tracer density

Simulation Setup

How did the disk acquire its AM?

Requires the knowledge of the Lagrangian evolution of the gas

⇒ now possible using tracer particles

Let look at the filamentary accretion of cold gas at z≥2

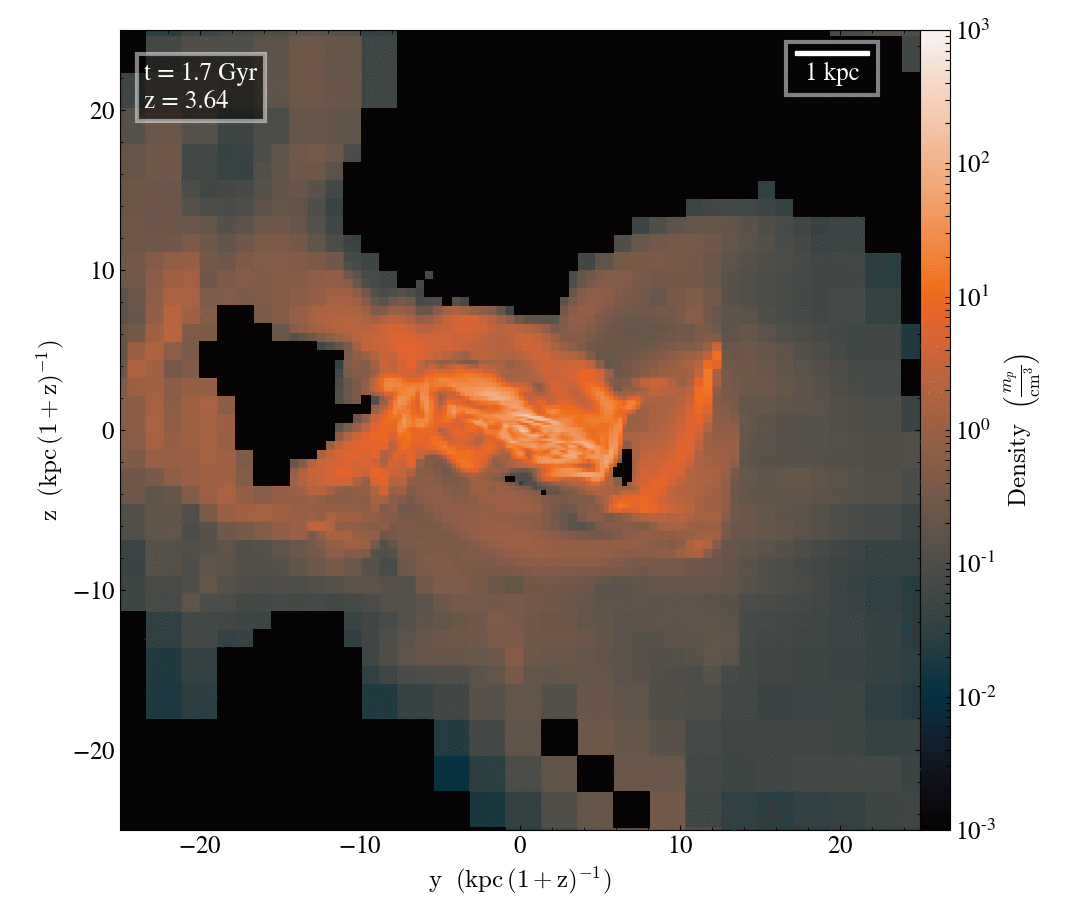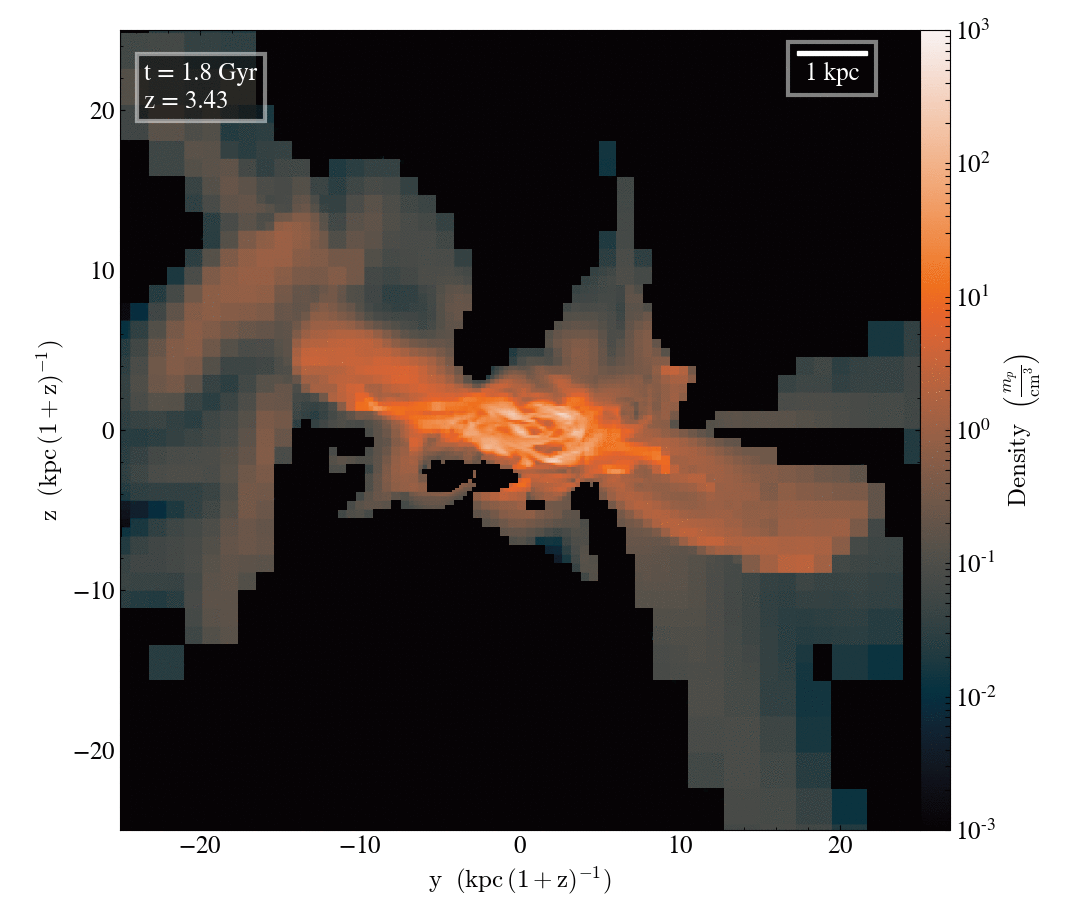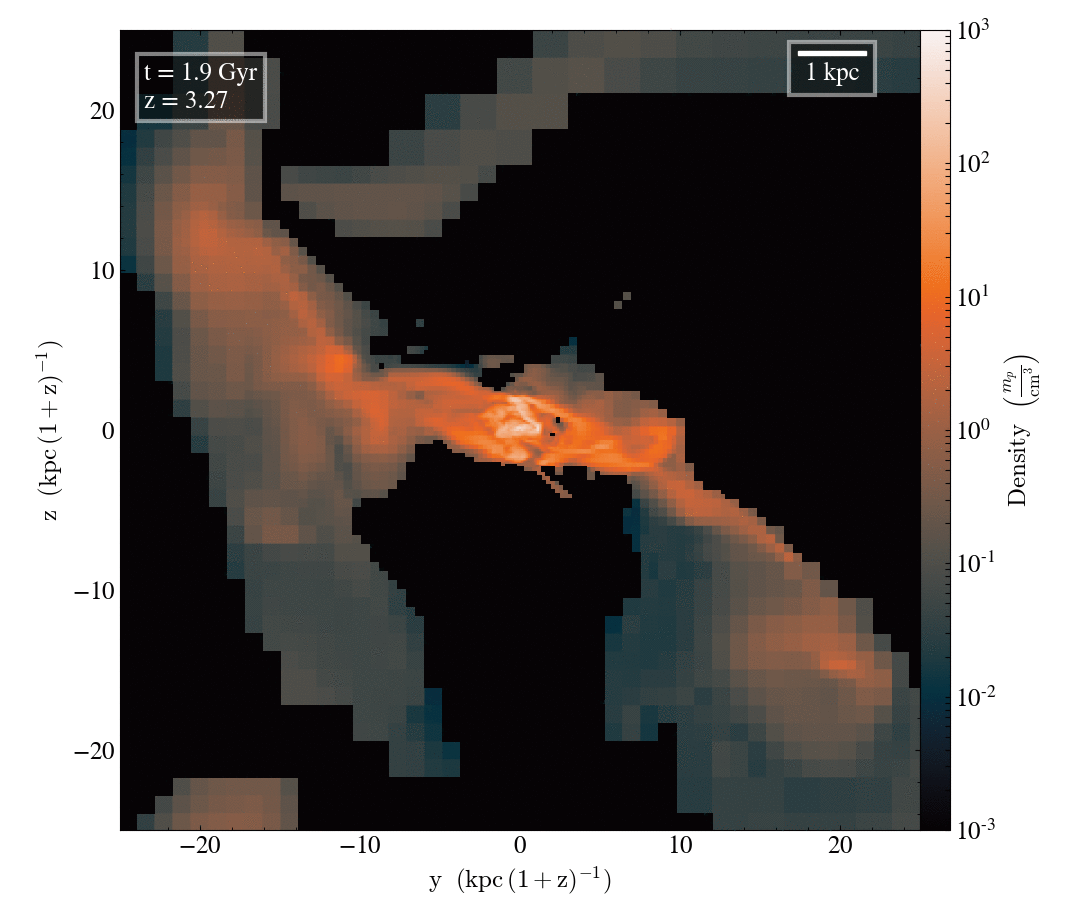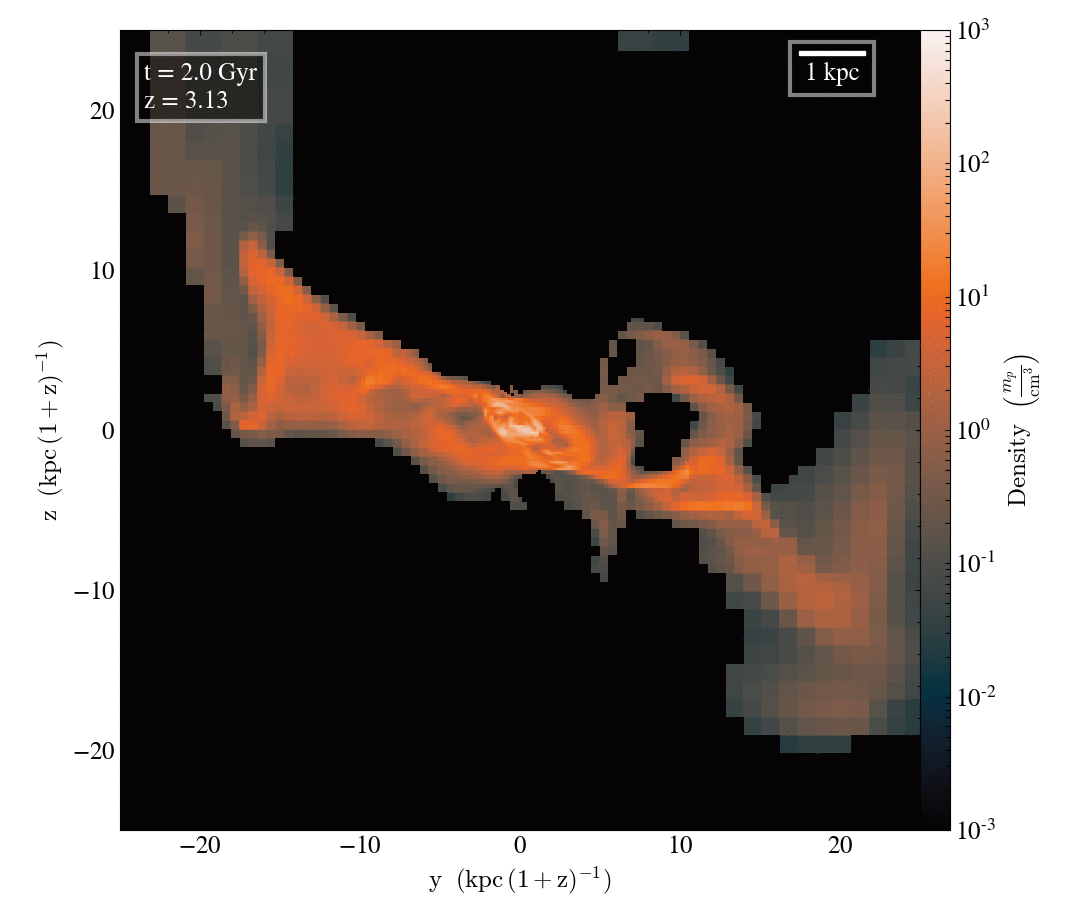
How does the cosmic web impact galaxy formation

By Corentin Cadiou

Made with Slides.com

How does the cosmic web impact galaxy formation

Presentation at Cambridge on 31/11/2018

  • 168

More from Corentin Cadiou