Limiting shape for first-passage Percolation models
on random geometric graphs
Cristian F. Coletti (UFABC)
Overview
- Introduction to First-passage percolation (FPP)
- Random geometric graphs (RGG)
- First-passage percolation
- Asymptotic shape theorem
- Richardson model
Overview
19/19056-2
20/12868-9
17/10555-0
- Introduction to First-passage percolation (FPP)
- Random geometric graphs (RGG)
- First-passage percolation
- Asymptotic shape theorem
- Richardson model
Lucas R. de Lima (UFABC)
Joint work with
Daniel Valesin (Warwick)
Alexander Hinsen (WIAS - Berlin)
Benedikt Jahnel (WIAS - Berlin)
Supported by
What is it about?
first passage percolation on
- Introduced by Hammersley and Welsh in 1965 as a model for the spread of a fluid.
- Attach a nonnegative R.V. t(e) so that the (t(e) : e is and edge) is I.I.D.
- t(e) is interpreted as a passage time (or time needed to cross e).
- Define the shortest time to connect x to y by
Zd
\mathbb{Z}^d
T(x,y)=inf{e∈γ:x→y∑t(e)}
T(x,y) = \inf \{\displaystyle \sum_{e \in \gamma : x \rightarrow y} t(e)\}
The infimum is over all paths connecting x to y. Recall that a path is a finite sequence of vertices and edges
(v0,e1,v1,...,en,vn)
(v_0,e_1,v_1,...,e_n,v_n)
such that
v0=x,vn=y,ei=(vi−1,vi).
v_0=x, v_n=y, e_i=(v_{i-1},v_i).
FIRST-PASSAGE PERCOLATION
Time constant
It is of interest to study the asymptotic behavior of
T(0,nx).
T(0,nx).
Under some assumption on the distribution of t(e) we get
n→∞limnT(0,nx)=μ(x) a.s.−L1,x∈Zd
\displaystyle\lim_{n \rightarrow \infty} \frac{T(0,nx)}{n} = \mu(x) \ \ \ a.s. - L^1, x \in \mathbb{Z}^d
when this limit exists and we call μ(e1) the time constant.
\text{when this limit exists and we call} \ \mu(e_1) \ \text{the time constant.}
Time constant
(T(nx,mx))1≤n≤m
(T(nx,mx))_{1 \leq n \leq m}
Remark: This follows from the sub-additivity of the sequence
Idea: It follows from the translation invariance of the model that
E[T(0,(n+m)x)]≤E[T(0,nx)]+E[T(0,mx)] ∀ m,n≥1.
\mathbb{E}[T(0,(n+m)x)] \leq \mathbb{E}[T(0,nx)] + \\
\mathbb{E}[T(0,mx)] \ \forall \ m,n \geq 1.
Time constant
Fekete´s lemma and finite first moment of
T(0,x)
T(0,x)
guarantees that
n→+∞limnE[T(0,nx)]
\displaystyle \lim_{n \rightarrow +\infty} \frac{\mathbb{E}[T(0,nx)]}{n}
exists and it is finite. Name this limit
μ(x)
\mu(x)
Time constant
That
n→+∞limnT(0,nx)=μ(x)
\displaystyle \lim_{n \rightarrow +\infty} \frac{T(0,nx)}{n} = \mu(x)
follows from Kingman´s - Liggett subadditive ergodic theorem applied to the sequence
(T(nx,mx):0≤n<m), x∈Zd.
\left(T(nx,mx) : 0 \leq n < m \right), \ \ \ x \in \mathbb{Z}^d .
Time constant
Remark: The time constant has been defined only for
x∈Zd.
x \in \mathbb{Z}^d.
Then extend the time constant to the whole space using
Remark: Kesten (1984) proved that we can use K-L theorem under the assumption
∙ The uniform continuity of the time constant on Qd and
\bullet \ \text{The uniform continuity of the time constant on} \ \mathbb{Q}^d \ \text{and}
∙ The density of Qd on Rd.
\bullet \ \text{The density of} \ \mathbb{Q}^d \ \text{on} \ \mathbb{R}^d .
Time constant
E[min{t1,…,t2d}]<+∞
\mathbb{E}[\min\{t_1, \ldots, t_{2d}\}] < +\infty
where the R.V. in the minimum are i.i.d. copies of the passage time.
- Kesten (1984) proved that the time constant is a norm in the whole space if and only if
ν({0})<pc(d).
\nu(\{0\}) < p_c(d) .
Then,
Time constant
- Cox-Durrett (1981) proved that if conditions
ν({0})<pc(d)
\nu(\{0\}) < p_c(d)
and
E[min{t1d,…,t2dd}]<+∞
\mathbb{E}[\min\{t^d_1, \ldots, t^d_{2d}\}] < +\infty
(1−ϵ)B⊂t1B(t)⊂(1+ϵ)B.
\left(1-\epsilon\right) \mathfrak{B} \subset \frac{1}{t} B(t) \subset \left(1+ \epsilon\right) \mathfrak{B} .
hold, then for any ϵ>0 a.s ∃M:∀t≥M
\text{hold, then for any} \ \epsilon > 0 \ \text{a.s} \ \exists M : \forall t \geq M
Time constant
∙ Indeed, B is the unit ball for the norm μ.
\bullet \ \text{Indeed,} \ \mathfrak{B} \ \text{is the unit ball for the norm} \ \mu .
∙ Recently, Cerf-Theˊret (2016) proved that ifν([0,∞))>pc(d)and ν({0})<pc(d)a limit shape theorem holds (for the fattened version).
\bullet \ \text{Recently, Cerf-Théret (2016) proved that if} \\
\nu \left([0,\infty)\right) > p_c(d) \text{and} \ \nu \left(\{0\}\right) < p_c(d) \\
\text{a limit shape theorem holds (for the fattened version).}
∙ Here, B(t) is the set of points that can be reached from
\bullet \ \text{Here,} \ B(t) \ \text{is the set of points that can be reached from}
the origin by time t. (fattened version)
\text{the origin by time} \ t. \ \text{(fattened version)}
FIRST-PASSAGE PERCOLATION
First-passage percolation
The model
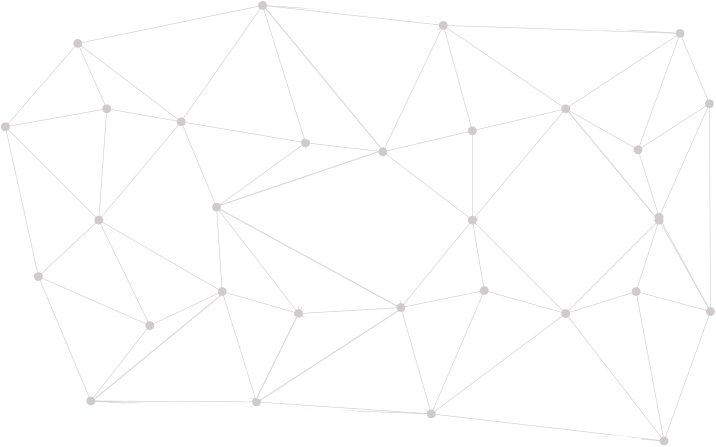
Random geometric graph
Let Pλ be the random set of points determined bythe homogeneous PPP on Rd with intensity λ>0.
\text{Let} \ \mathcal{P}_\lambda \ \text{be the random set of points determined by} \\
\text{the homogeneous PPP on} \ \mathbb{R}^d \ \text{with intensity} \ \lambda>0.
∙ The RGG Gλ,r=(V,E) on Rd is defined by
\bullet \ \text{The RGG} \ \mathcal{G}_{\lambda,r}=(V,E) \ \text{on} \ \mathbb{R}^d \ \text{is defined by}
V=Pλ and E={{u,v}⊆V:∣∣u−v∣∣<r, u=v},
V = \mathcal{P}_\lambda \ \text{and} \ E = \big\{\{u,v\} \subseteq V: ||u-v|| < r , \ u \neq v\big\},
where ∣∣⋅∣∣ is the Euclidean norm.
\ \ \text{where} \ ||\cdot|| \ \text{is the Euclidean norm.}
The model
Remark:
∙ We want to study the spread of an infectionon an infinite connected component of Gλ,r.
\bullet \ \text{We want to study the spread of an infection} \\
\text{on an infinite connected component of} \ \mathcal{G}_{\lambda , r}.
∙ For all d≥2 ∃ rc(λ)>0:Gλ,r has an infinite component
\bullet \ \text{For all} \ d \geq 2 \ \exists \ r_c(\lambda)>0 : \mathcal{G}_{\lambda , r} \ \text{has an infinite component}
H, a.s. for all r>rc(λ) which is a.s. unique.
\mathcal{H}, \ \textit{a.s.} \ \text{for all} \ r > r_c(\lambda) \ \text{which is} \ \textit{a.s.} \ \text{unique.}
The model
∙ H is a subgraph of Gλ,r.
\bullet \ \mathcal{H} \ \text{is a subgraph of} \ \mathcal{G}_{\lambda , r}.
∙ Denote by (V(H),E(H)) the resulting graph.
\bullet \ \ \text{Denote by} \ \left(V(\mathcal{H}), E(\mathcal{H})\right) \ \text{the resulting graph.}
∙ It is well known that rc(1)≥1/υd1/d here υd denotes
\bullet \ \text{It is well known that} \ r_c (1) \geq 1/{\upsilon_d}^{1/d} \ \text{here} \ \upsilon_d \ \text{denotes}
the volume of the d−dimensional unit ball.
\text{the volume of the} \ d-\text{dimensional unit ball.}
q(x)=arg miny∈V(H)∥y−x∥
q(x)= \operatorname{arg~min}_{y\in V(\mathcal{H})} \|y-x\|
Let us define for every x∈Rd
\text{Let us define for every} \ x \in \mathbb{R}^d
Existe
Voronoi partition
q induces a Voronoi partition of Rd with respect to H.
q \ \text{induces a Voronoi partition of} \ \mathbb{R}^d \ \text{with respect to} \ \mathcal{H} .
Voronoi partition
FIRST-PASSAGE PERCOLATION
We assign a random length
τe≥0
\tau_e \geq 0
to each edge
e∈E(H).
e \in E(\mathcal{H}).
Let
{τe}e∈E(H)
\{\tau_e\}_{e \in E(\mathcal{H})}
be independent and identically distributed with
τe∼τ.
\tau_e \sim \tau.
FIRST-PASSAGE PERCOLATION
We define the passage time between by the random variable
x,y∈Rd
x,y \in \R^d
T(x,y):=inf{∑e∈γτe:γ∈P(q(x),q(y))}
T(x,y) := \inf\left\{\sum_{e\in\gamma} \tau_{e}: \gamma\in\mathscr{P(q(x),q(y))}\right\}
FIRST-PASSAGE PERCOLATION
Let denote the random set of regions (Voronoi cells)
reached up to time t with the FPP starting from q(o).
Ht
H_t
Ht:={x∈Rd:T(o,x)<t}
H_t := \big\{ x \in \mathbb{R}^d: {T(o,x) < t} \big\}
Asymptotic shape theorem
Set
(A1)
P(τ=0)<(υdrdλ).1;
\mathbb{P}(\tau = 0) < \dfrac{1}{(\upsilon_d r^d\lambda).} \quad;
(A2)
E[τη]<+∞.
\mathbb{E}[\tau^\eta] < +\infty.
There exists
η>2(d+1)
\eta > 2(d + 1)
such that
Asymptotic shape theorem
Let
d≥2
d \geq 2
and
r>rc
r > r_c
Then there exists
one has
φ>0
\varphi > 0
such that, for all
a.s.
\text{a.s.}
for
n≫1.
n \gg 1.
(1−ε)B(φ)⊆n1Hn⊆(1+ε)B(φ)
(1-\varepsilon)B(\varphi) \subseteq \frac{1}{n}H_n \subseteq (1+\varepsilon)B(\varphi)
. Consider i.i.d. FPP on a RGG
satisfying (A1) and (A2)
ε∈(0,1)
\varepsilon \in (0,1)
that
Sketch of the proof
- The passage time grows at most linearly
- The passage time grows at least linearly
- We apply Kingman`s subadditive ergodic theorem
Shape
- Consequence of the rotational invariance
At most linear growth
E[T(o,x)]≥a∥x∥.
\mathbb{E}[T(o,x)] \geq a \|x\|.
Condition (A1) implies that there exists such that
a>0
a>0
At Least linear growth
P(T(o,x)>t)<c⋅t−(d+κ).
\mathbb{P}\Big(T(o,x) > t\Big) < c \cdot t^{-(d+\kappa)}.
Condition (A2) implies that there exist such that
for each and all , one has that
β,κ>1
\beta,\kappa>1
x∈Rd
x \in \mathbb{R}^d
t≥β∥x∥
t \geq \beta \|x\|
Subadditive ergodic theorem
limn→∞∥nx∥T(o,nx)=φ−1a.s.
\lim_{n\to\infty} \dfrac{T(o,nx)}{\|nx\|} = {\varphi}^{-1} \quad \text{a.s.}
(Kingman)
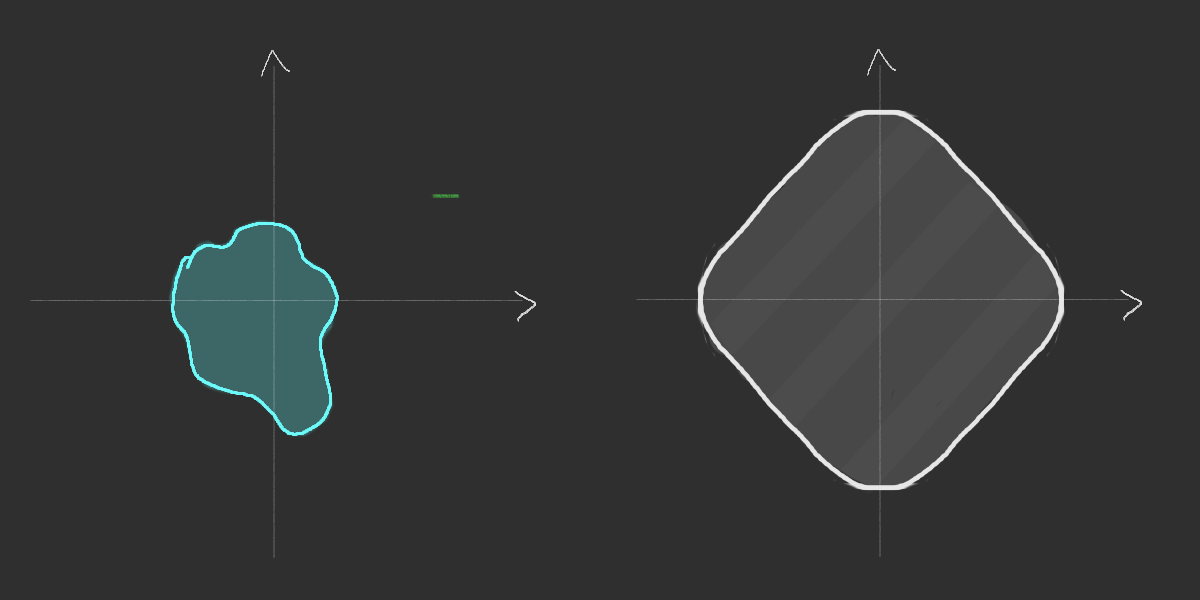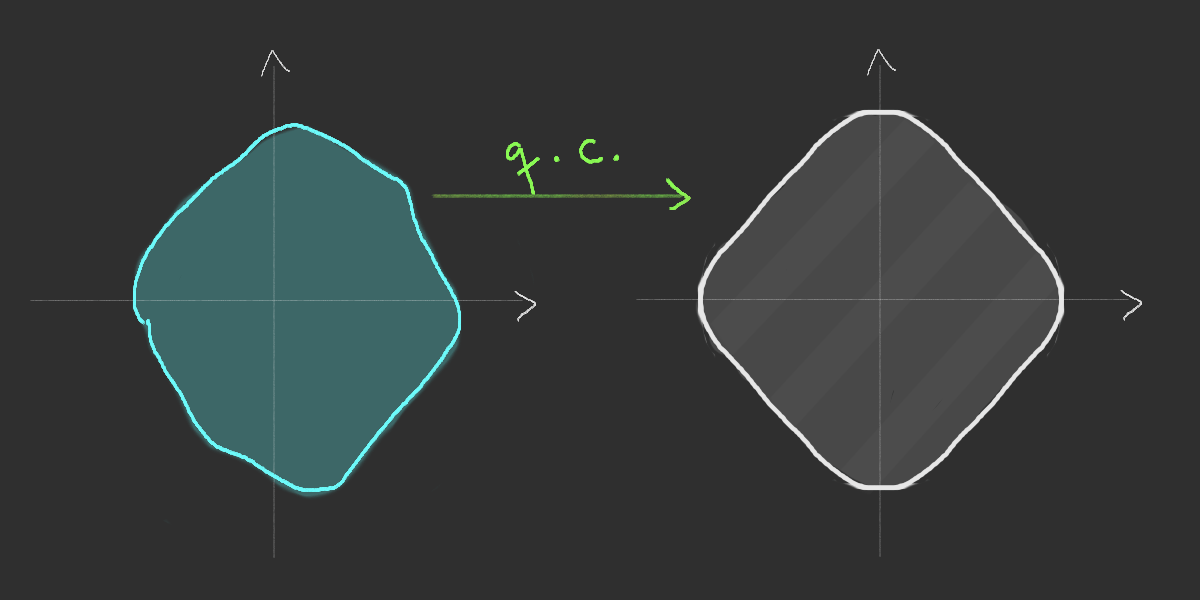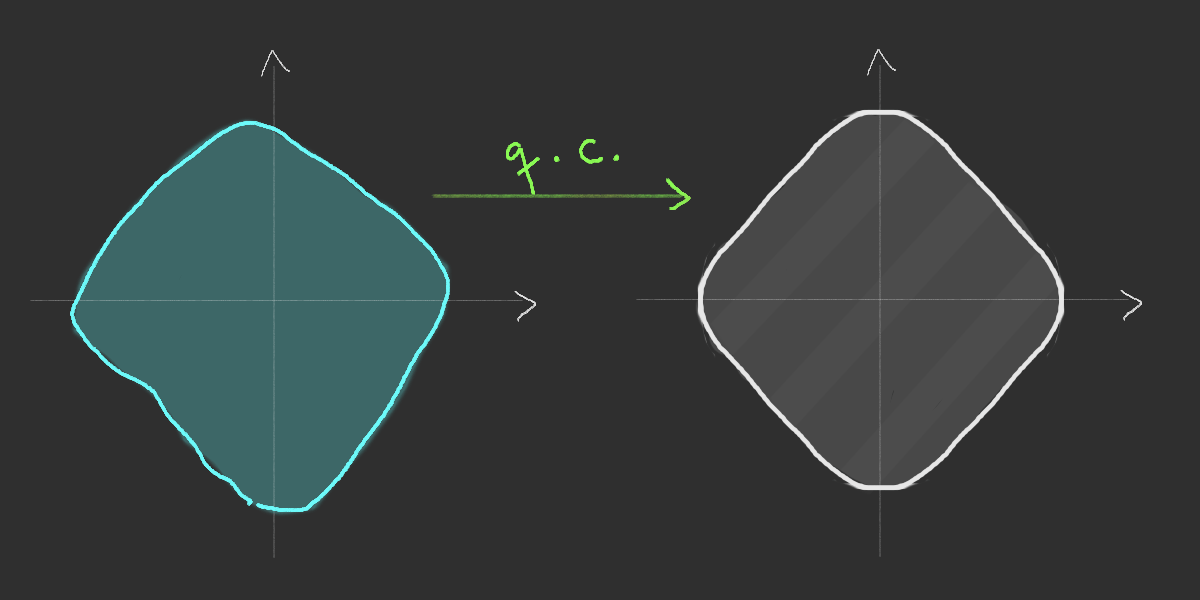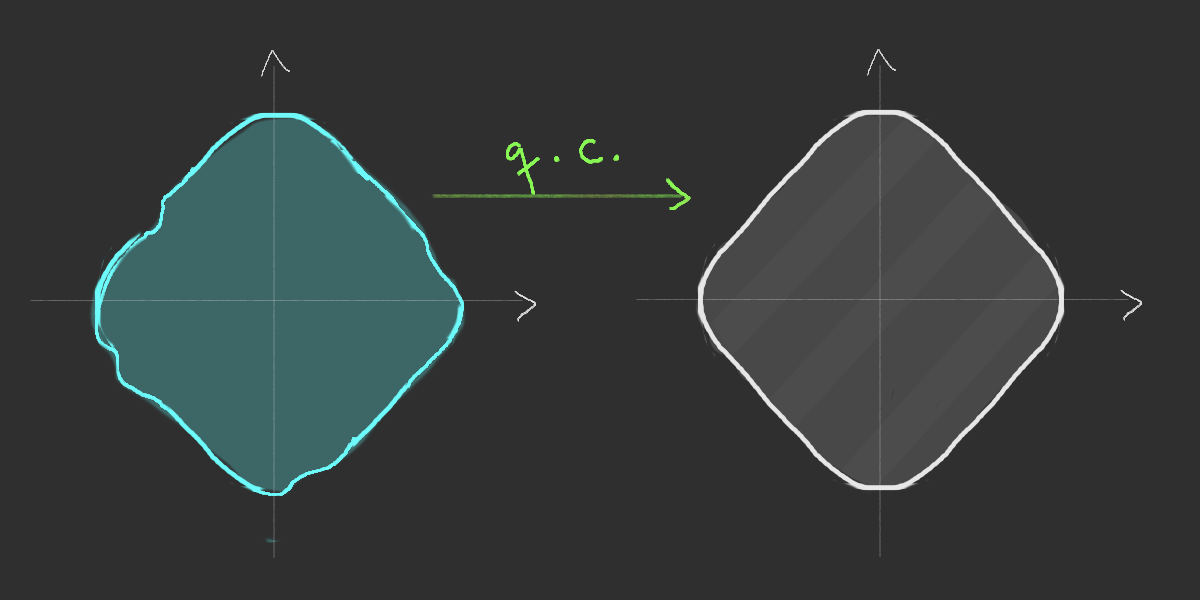
Asymptotic equivalence
∥x∥→+∞lim∥x∥T(o,x)=φ−1a.s.
\lim\limits_{\|x\|\to+\infty}\dfrac{T(o,x)}{\|x\|} = {\varphi}^{-1} \quad \text{a.s.}
Existence of the limiting shape
Simulation of the Richardson's infection model
Richardson's growth model (1973)
∙ At t≥0, a site of H is either healthy (0) or infected (1).
\bullet \ \text{At} \ t \geq 0, \ \text{a site of} \ \mathcal{H} \ \text{is either } \ \text{healthy (0) or infected (1). }
∙ ζt:V(H)→{0,1} denotes the state of the sites at time t
\bullet \ \zeta_t:V(\mathcal{H})\to \{0,1\} \ \text{denotes the state of the sites at time t}
∙ Model the spread of an infection (growth of a population).
\bullet \ \text{Model the spread of an infection (growth of a population).}
RICHARDSON'S GROWTH MODEL
∙ The process evolves as follows:
\bullet \ \text{The process evolves as follows:}
∙ A healthy particle becomes infected at rate
\bullet \ \text{A healthy particle becomes infected at rate}
λI∑y∼xζt(y).
\lambda_{I}\sum_{y \sim x}\zeta_t(y).
∙ An infected particle remains infected forever.
\bullet \ \text{An infected particle remains infected forever.}
RICHARDSON'S GROWTH MODEL
∙ The process is determined by FPP with edge passage times
\bullet \ \text{The process is determined by FPP with edge passage times}
τe∼Exp(λI)
\tau_e \sim \mathrm{Exp}(\lambda_{I})
independently for each e∈E(H).
\text{independently for each} \ e \in E(\mathcal{H}).
RICHARDSON'S GROWTH MODEL
∙ Condition (A1) is straightforward since
\bullet \ \text{Condition} \ (A_1) \ \text{is straightforward since}
∙ Condition(A2) holds since
\bullet \ \text{Condition} (A_2) \ \text{holds since}
P(τ=0)=0<1/(υdrdλ).
\mathbb{P}(\tau=0)=0<1/(\upsilon_d r^d\lambda).
E[exp(ατ)]<+∞ for α∈(0,λrI).
\ \mathbb{E}[\exp(\alpha\tau)] < +\infty \ \text{for} \ \alpha \in (0, \lambda_{r I}).
RICHARDSON'S GROWTH MODEL
∙ The shape theorem holds for the Richardson model on H
\bullet \ \text{The shape theorem holds for the Richardson model on}
\ \mathcal{H}
for any r>rc(λ).
\text{for any} \ r > r_c(\lambda).
Time-space rescaling for Richardson model
∙ Asymptotic behavior of the Richardson model
\bullet \ \text{Asymptotic behavior of the Richardson model}
∙ The limiting process is a branching process
\bullet \ \text{The limiting process is a branching process}
(Ttλ,λI)t≥0.
(\mathcal{T}^{\lambda,\lambda_{I}}_t)_{t\geq 0}.
The limit object
\text{The limit object}
∙ T0λ,λI=o.
\bullet \ \mathcal{T}^{\lambda,\lambda_{I}}_0=o.
TIME-SPACE RESCALING FOR RICHARDSON MODEL
∙ Offsprings are given by PPP(υdrdλλI) (time)
\bullet \ \text{Offsprings are given by PPP}(\upsilon_d r^d\lambda\lambda_{I}) \ \text{ (time)}
∙ Offsprings are placed independently and uniformly within
\bullet \ \text{Offsprings are placed independently and uniformly within}
Br(Xi).
B_r(X_i).
TIME-SPACE RESCALING FOR RICHARDSON MODEL
Let r>rc(λ). Then,
\text{Let} \ r > r_{c}(\lambda). \ \text{Then,}
H[0,t]αλ,λI/α⟶T[0,t]λ,λI
\mathcal{H}_{[0,t]}^{\alpha \lambda, \lambda_{I}/\alpha} \longrightarrow \mathcal{T}^{\lambda, \lambda_{I}}_{[0,t]}
weakly with respect to the Skorokhod topology, as
\text{weakly with respect to the Skorokhod topology, as }
α→∞
\alpha \rightarrow \infty
TIME-SPACE RESCALING FOR RICHARDSON MODEL
Remark:
The subscript [0,t] indicates that we consider the whole path from
\text{The subscript} \ [0,t] \ \text{indicates that we consider the whole path from}
0 to t.
\ 0 \ \text{to} \ t.
Ongoing work
Lucas R. de Lima, D. Valesin, C. F. C.
∙ Quantitative shape theorem for FPP on RGG
\bullet \ \text{Quantitative shape theorem for FPP on RGG}
∙ Moderate deviation for the passage time
\bullet \ \text{Moderate deviation for the passage time}
∙ A dynamic on RGGs
\bullet \ \text{A dynamic on RGGs}
Thank you!
Preprint available on
arxiv:2109.07813
Limiting shape for first-passage Percolation models on random geometric graphs Cristian F. Coletti (UFABC)
UFRJ 2022
By Cristian Coletti
UFRJ 2022
- 241
