Applied Measure Theory

for Probabilistic Modeling

Chad Scherrer

July 2023

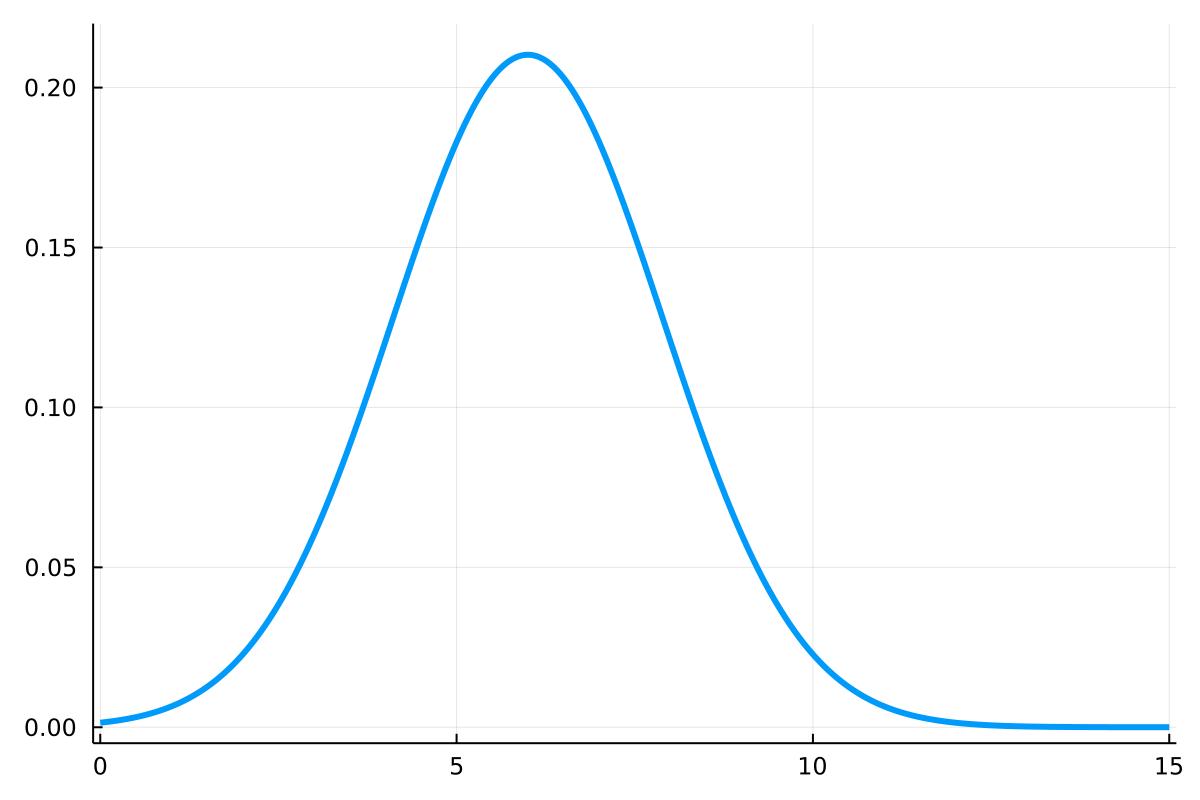
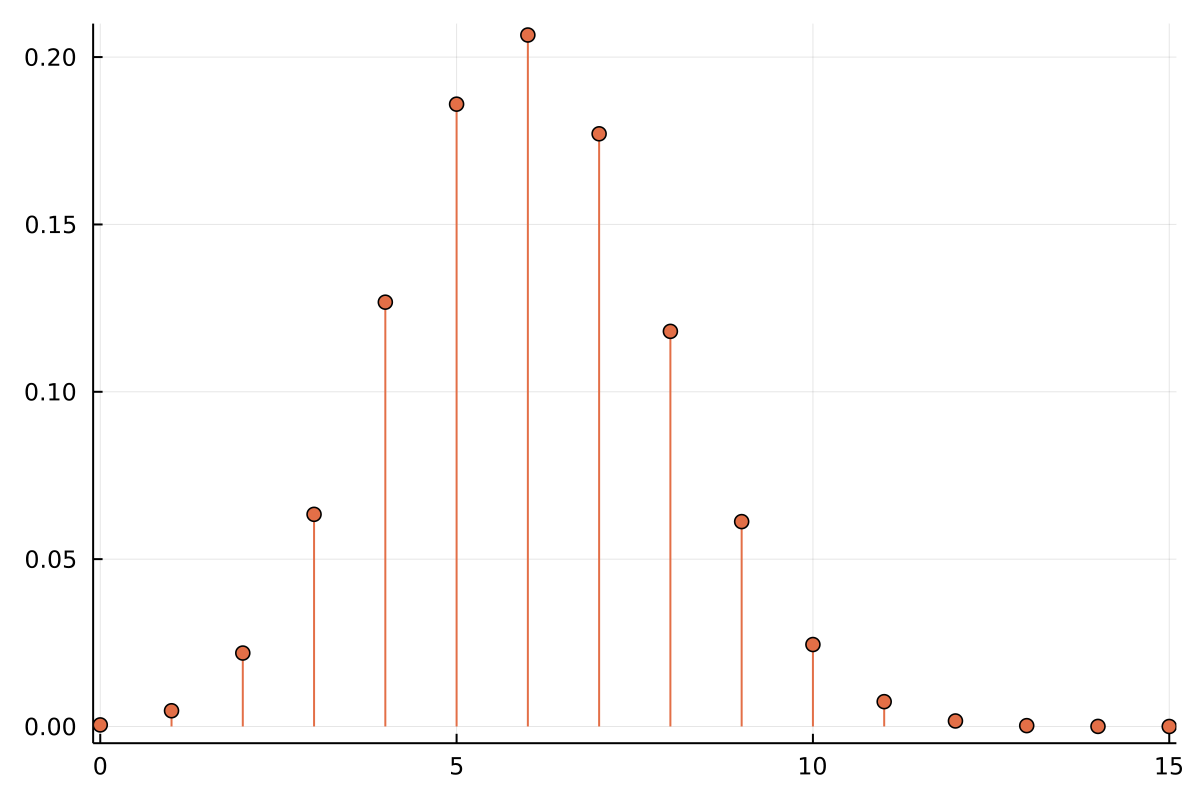
Discrete Distributions

  • Expressed as a probability mass function
  • Evaluation gives a probability
  • Values sum to one

Continuous Distributions

  • Expressed as a probability density function
  • Evaluation gives a probability density
  • Values integrate to one
\sum_j f(x_j) = 1
\int_{-\infty}^\infty f(x)\ dx = 1

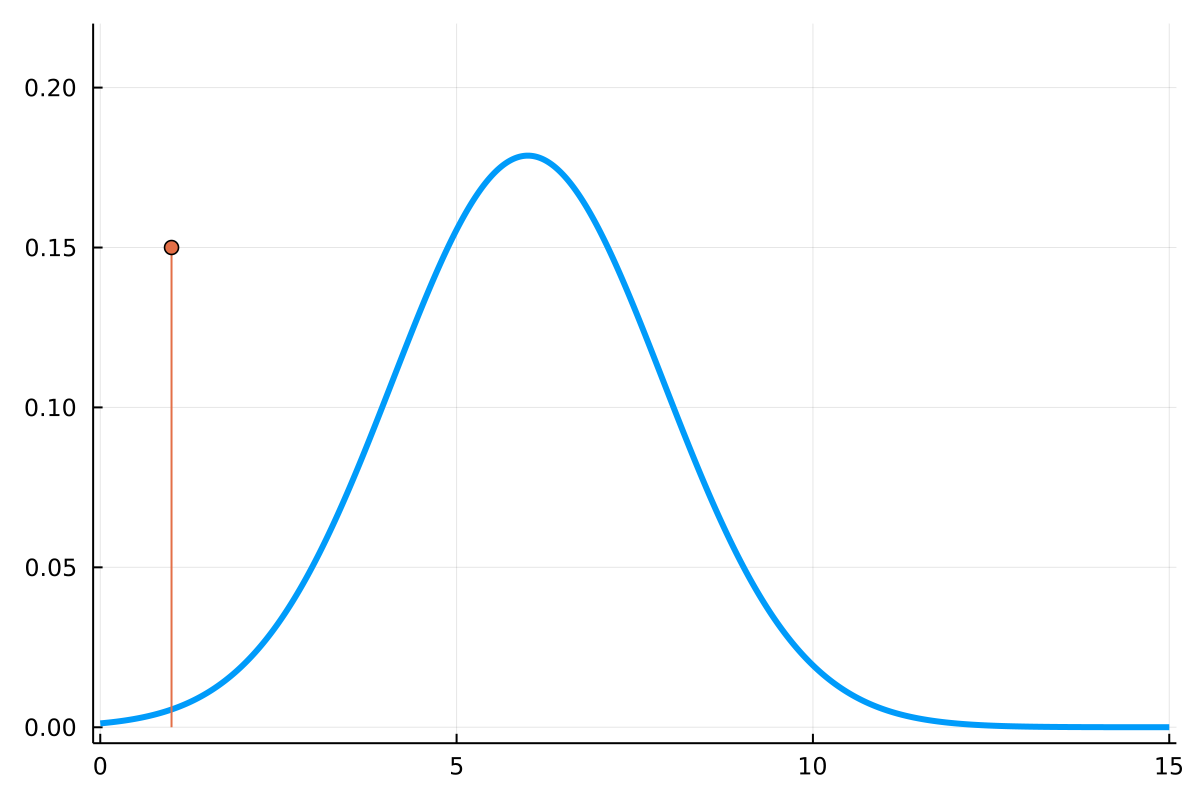
Discrete/Continuous Mixtures

  • What is    ?
  • How is it interpreted?
  • What is "integration"?
  • How do we compute this?
f
discrete_part = Dirac(1)
continuous_part = Normal(15 * 0.4, sqrt(15 * 0.4 * 0.6))

m = 0.15 * discrete_part + 0.85 * continuous_part

In MeasureTheory.jl:

\text{To approximate } \mathbb{E}_{x \sim p}\left[ f(x) \right]
\text{Choose some proposal, } q(x)
\text{Then approximate } \mathbb{E}_{x \sim q}\left[ f(x) {\color{red} \frac{p(x)}{q(x)}} \right]
\text{To sample from unnormalized } \tilde{p}(x)
\text{Accept when } M u < {\color{red} \frac{\tilde{p}(x)}{q(x)}} \text{, otherwise reject}
\text{Find sampleable } q(x) \text{, and } M \text{ such that } {\color{red} \frac{\tilde{p}(x)}{q(x)}} \le M
\text{Sample } u \sim \text{Uniform, and } x \sim q
\text{Sample } u \sim \text{Uniform, and } x' \sim q(x' \mid x)
\text{Accept when } u < \left. {\color{red} \frac{\tilde{p}(x')}{q(x'\mid x)} } \middle/ {\color{red} \frac{\tilde{p}(x)}{q(x\mid x')} } \right. \text{, otherwise reject}
\text{Given sample } x \text{ and proposal } q(x' \mid x),
\text{KL}(p\; \|\; q) = \mathbb{E}_{x\sim p}\left[ {\color{red} \frac{p(x)}{q(x)}} \right]
\text{Given ``true'' distribution } p
\text{ and approximating distribution } q,
\frac{p(x)}{q(x)} \text{ is really } \frac{dp}{dq}(x) = \left. \frac{dp}{d\lambda}(x) \middle/ \frac{dq}{d\lambda}(x) \right.
p
q
\lambda

Densities are always relative!

Densities are always relative

  • Old and very standard idea (Lebesgue, Radon, Nikodym)
  • But no other software we know of makes this explicit!
function basemeasure(::Normal{()})
  WeightedMeasure(static(-0.5 * log2π), LebesgueMeasure())
end

function logdensity_def(d::Normal{()}, x)
  -x^2 / 2
end

Computational advantages

  • Easily represent more complex measures than usually possible
  • Common structure can share computation
  • Static computation makes this fast
  • But no other software we know of makes this explicit!

Each measure has a base measure...

.. and a log-density relative to that base measure

What actually happens when you call logdensityof(Normal(5,2), 1)?

Affine((μ=5, σ=2), Normal())

Normal(5,2)

proxy

insupport(Affine(...), 1)

✓

0.5 * LebesgueMeasure()

basemeasure

LebesgueMeasure()

basemeasure

ℓ == -3.6121

basemeasure

0.3989 * Affine((μ=5, σ=2), LebesgueMeasure())

\frac{1}{\sqrt{2 \pi}} \approx

ℓ = 0.0

ℓ += -2.0

-\frac{1}{2}\left(\frac{x-\mu}{\sigma}\right)^2

ℓ += -0.9189

\log \frac{1}{\sqrt{2 \pi}} \approx

ℓ += -0.6931

\log \frac{1}{2} \approx

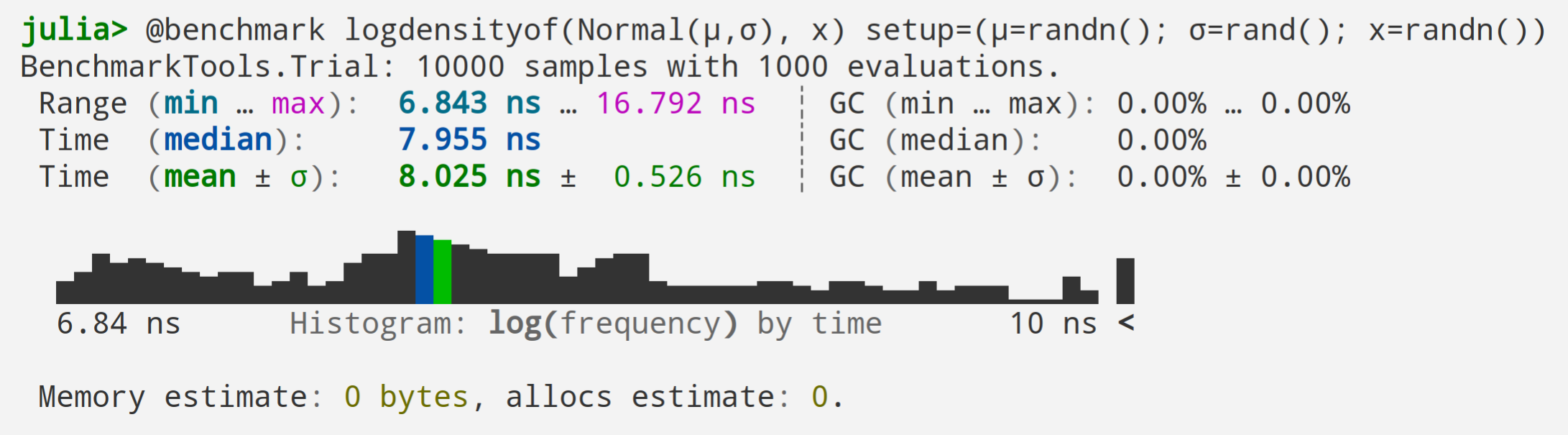
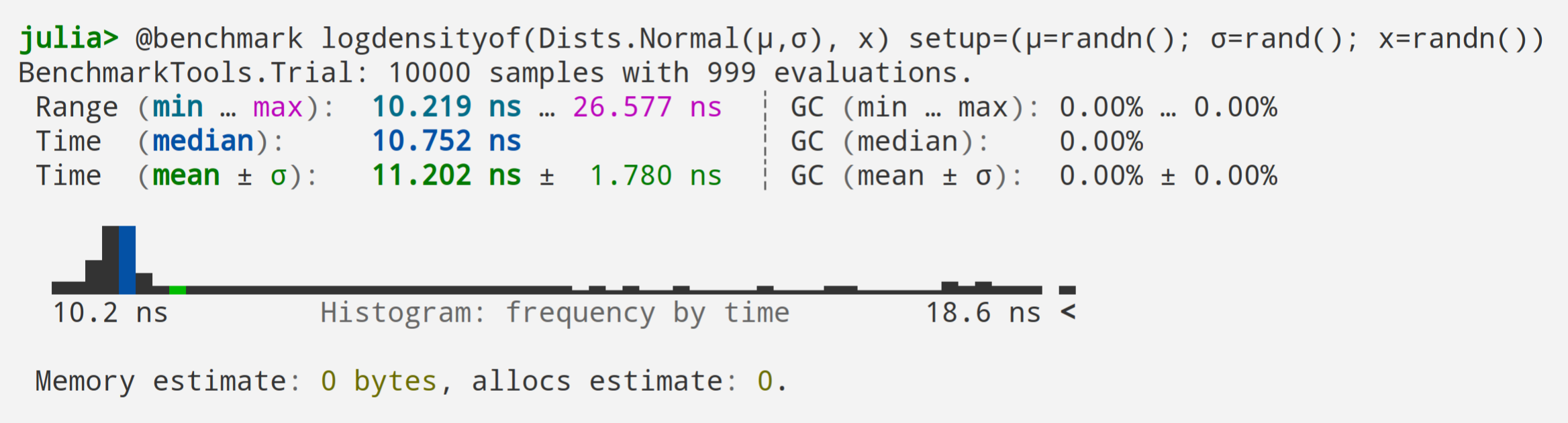
Distributions.jl

MeasureTheory.jl

\text{Lebesgue}(\mathbb{R})
\text{Beta}(\alpha, \beta)
\frac{1}{\sqrt{2\pi}}\text{Lebesgue}(\mathbb{R})
\text{Normal}(\mu, \sigma^2)
\text{Lebesgue}(\mathbb{I})

+

—

+

—

Ways of writing Normal(0,2)

-\log {\color{darkorange} \sigma} - \frac{1}{2}\left(\frac{x - \color{blue} \mu}{\color{darkorange} \sigma}\right)^2
Normal(0,2)
Normal(μ=0, σ=2)
Normal(σ=2)
Normal(mean=0, std=2)
Normal(mu=0, sigma=2)
\frac{1}{2} \left( \log({\color{darkorange} τ}) - {\color{darkorange} τ} (x - {\color{blue} μ})^2 \right)
Normal(μ=0, τ=0.25)
-\frac{1}{2} \left( \log {\color{darkorange} \sigma^2} - \frac{(x - {\color{blue} \mu})^2}{\color{darkorange} \sigma^2} \right)
Normal(μ=0, σ²=4)
Normal(mean=0, var=4)
-{\color{darkorange} \log \sigma} - \frac{(x - {\color{blue} μ})^2}{2 e^{2 {\color{darkorange} \log \sigma}}}
Normal(μ=0, logσ=0.69)

A measure can be primitive or defined in terms of existing measures

Primitive Measures

  • TrivialMeasure
  • LebesgueMeasure
  • CountingMeasure

Product-like

  • ProductMeasure (⊗)
  • PowerMeasure (^)
  • For

Sum-like

  • SuperpositionMeasure (+)
  • SpikeMixture
  • IfElseMeasure (IfElse.ifelse)

Transformed Measures

  • PushforwardMeasure (pushfwd)
  • Affine (affine)

Density-related

  • WeightedMeasure (*)
  • PowerWeightedMeasure (↑)
  • PointwiseProductMeasure (⊙)
  • ParameterizedMeasure
  • DensityMeasure (∫)

Support-related

  • RestrictedMeasure (restrict)
  • HalfMeasure (Half)
  • Dirac
d = Beta(2,4) ^ (40,64)

A PowerMeasure produces replicates a given measure over some shape.

⋆

⋆Independent and Identically Distributed

d = For(40,64) do i,j
    Beta(i,j)
end
For(indices) do j
    # maybe more computations
    # ...
    some_measure(j)
end

For produces independent samples with varying parameters.

mc = Chain(Normal(μ=0.0)) do x Normal(μ=x) end
r = rand(mc)

Define a new chain, take a sample

julia> take(r,100) == take(r,100)
true

This returns a deterministic iterator

julia> logdensityof(mc, take(r, 1000))
-517.0515965372

Evaluate on any finite subsequence

prior = HalfNormal()
\begin{aligned} \color{#009cfa} \sigma &\color{#009cfa}\sim \text{Normal}_+(0,1) \\ \phantom{\color{#e47045} x_n} &\phantom{\color{#e47045} \sim \text{Normal}(0,\sigma} \end{aligned}
prior = HalfNormal()

d = Normal(σ=2.0) ^ 10
lik = likelihood(d, x)
\begin{aligned} \color{#009cfa} \sigma &\color{#009cfa}\sim \text{Normal}_+(0,1) \\ \color{#e47045} x_n &\color{#e47045} \sim \text{Normal}(0,\sigma) \end{aligned}
prior = HalfNormal()

d = Normal(σ=2.0) ^ 10
lik = likelihood(d, x)

post = prior ⊙ lik
\begin{aligned} \color{#009cfa} \sigma &\color{#009cfa}\sim \text{Normal}_+(0,1) \\ \color{#e47045} x_n &\color{#e47045} \sim \text{Normal}(0,\sigma) \end{aligned}
{\color{#3ba64c} P(\sigma | x)} \propto {\color{#009cfa} P(\sigma)} {\color{#e47045} P(x | \sigma)}
julia> using MeasureTheory, Symbolics

julia> @variables μ τ
2-element Vector{Num}:
 μ
 τ

julia> d = Normal(μ=μ, τ=τ) ^ 1000;

julia> x = randn(1000);

julia> ℓ = logdensityof(d, x) |> expand
500.0log(τ) + 3.81μ*τ - (503.81τ) - (500.0τ*(μ^2))
  • Types and functions are generic, so symbolic manipulations work out of the box
     
  • Compare
    • MeasureTheory.jl
    • Distributions.jl
julia> logdensityof(Distributions.Normal(μ, 1 / √τ), 2.0)
ERROR: MethodError: no method matching logdensityof(::Num, ::Float64)

Thank You!

https://github.com/cscherrer/MeasureTheory.jl

2023-06-MeasureTheory-Munich

By Chad Scherrer

2023-06-MeasureTheory-Munich

  • 291

More from Chad Scherrer