Soss: Lightweight Probabilistic Programming in Julia

Chad Scherrer

June 16, 2023

Making Rational Decisions

Managed Uncertainty

Rational Decisions

Bayesian Analysis

Probabilistic Programming

Physical systems
Hypothesis testing
Modeling as simulation

Medicine
Finance
Insurance

Risk

Custom models

The Two-Language Problem

A disconnect between the "user language" and "developer language"

Python

C

Deep Learning Framework

Harder for beginner users
Barrier to entry for developers
Limits extensibility

Introducing Soss

Simple high-level syntax
Uses GeneralizedGenerated.jl for flexible staged compilation
Model type parameter includes type-level representation of itself
Allows specialized code generation for each primitive(model, data)

A (Very) Simple Example

P(\mu,\sigma|x)\propto P(\mu,\sigma)P(x|\mu,\sigma)

\begin{aligned} \mu &\sim \text{Normal}(0,5)\\ \sigma &\sim \text{Cauchy}_+(0,3) \\ x_j &\sim \text{Normal}(\mu,\sigma) \end{aligned}

Theory

Soss

julia> Soss.sourceLogpdf()(m)
quote
    _ℓ = 0.0
    _ℓ += logpdf(HalfCauchy(3), σ)
    _ℓ += logpdf(Normal(0, 5), μ)
    _ℓ += logpdf(Normal(μ, σ) |> iid(N), x)
    return _ℓ
end

@model N begin
    μ ~ Normal(0, 5)
    σ ~ HalfCauchy(3)
    x ~ Normal(μ, σ) |> iid(N)
end

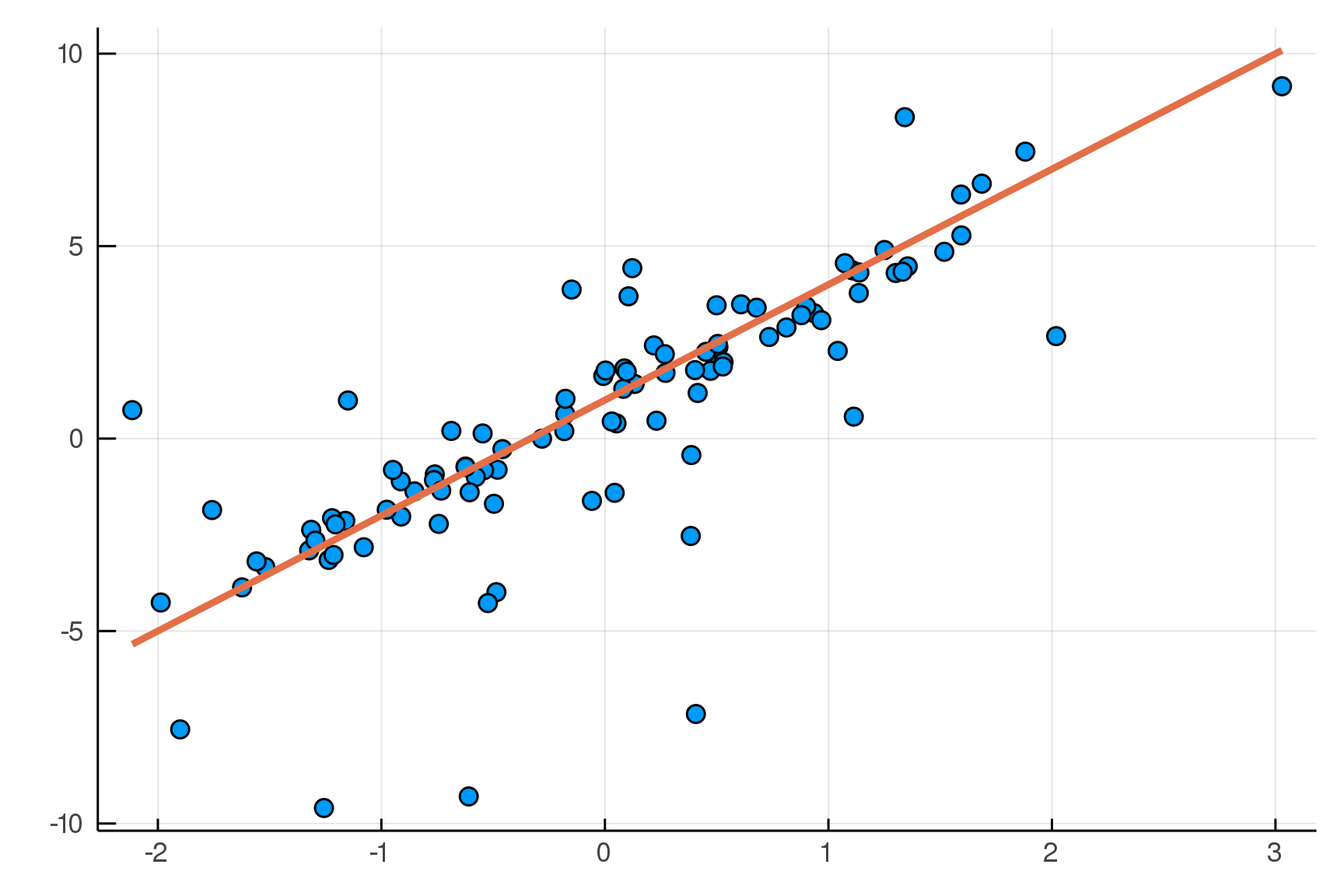
Building a Linear Model

m = @model x begin
    α ~ Normal()
    β ~ Normal()
    σ ~ HalfNormal()
    yhat = α .+ β .* x
    n = length(x)
    y ~ For(n) do j
        Normal(yhat[j], σ)
    end
end

julia> m(x=truth.x)
Joint Distribution
    Bound arguments: [x]
    Variables: [σ, β, α, yhat, n, y]

@model x begin
        σ ~ HalfNormal()
        β ~ Normal()
        α ~ Normal()
        yhat = α .+ β .* x
        n = length(x)
        y ~ For(n) do j
                Normal(yhat[j], σ)
            end
    end

Observed data is not specified yet!

Sampling from the Posterior Distribution

julia> post = dynamicHMC(m(x=truth.x), (y=truth.y,)) |> particles
(σ = 2.02 ± 0.15, β = 2.99 ± 0.19, α = 0.788 ± 0.2)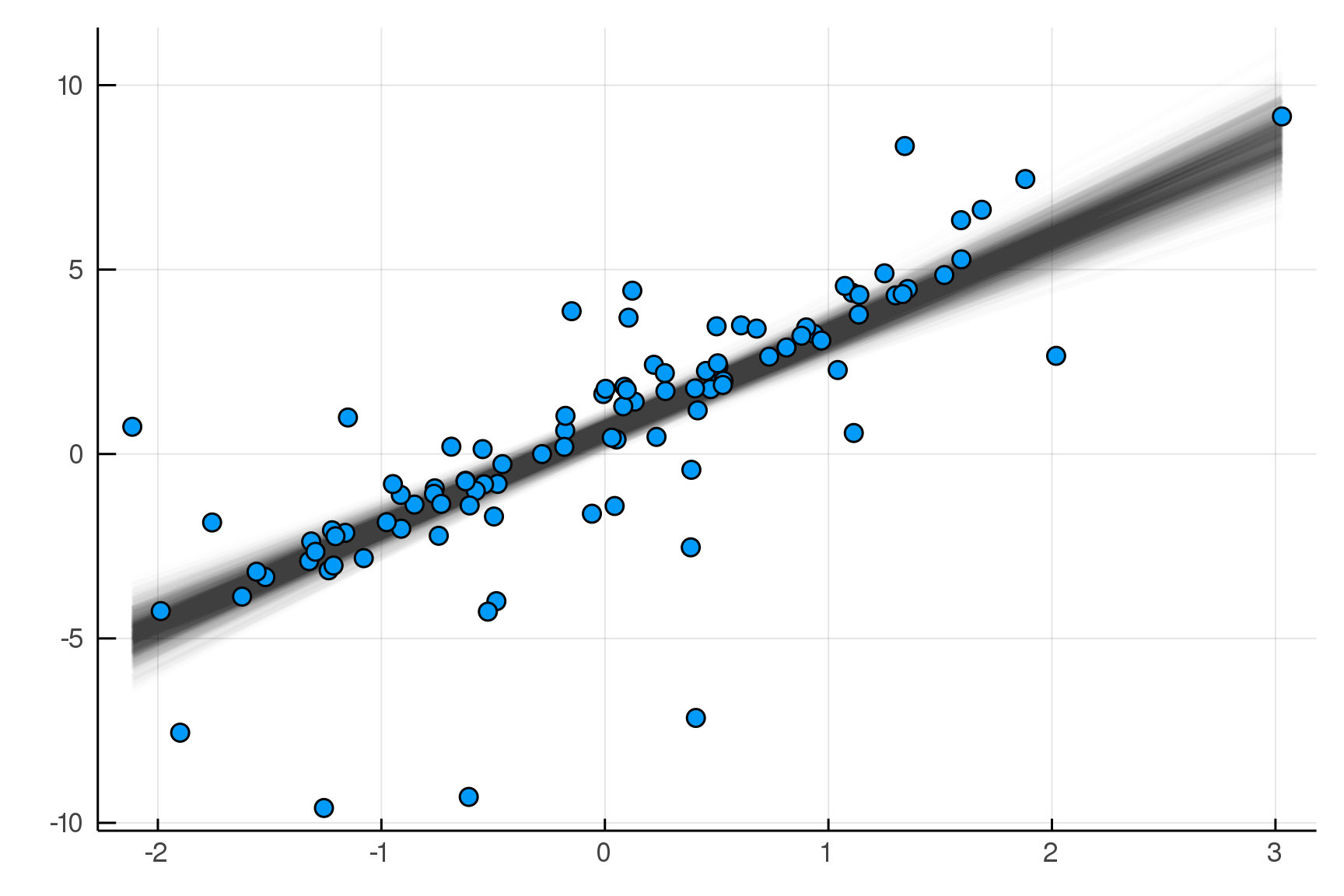

Posterior distribution

Possible best-fit lines

The Posterior Predictive Distribution

Start with Data

Sample Parameters|Data

Sample Data|Parameters

Real Data

Replicated Fake Data

Compare

Posterior

Distribution

Predictive

Distribution

The Posterior Predictive Distribution

pred = predictive(m, :α, :β, :σ)
@model (x, α, β, σ) begin
    yhat = α .+ β .* x
    n = length(x)
    y ~ For(n) do j
        Normal(yhat[j], σ)
    end
end

m = @model x begin
    α ~ Normal()
    β ~ Normal()
    σ ~ HalfNormal()
    yhat = α .+ β .* x
    n = length(x)
    y ~ For(n) do j
        Normal(yhat[j], σ)
    end
end

postpred = map(post) do θ 
    delete(rand(pred(θ)((x=x,))), :n, :x)
end |> particles

predictive makes a new model!

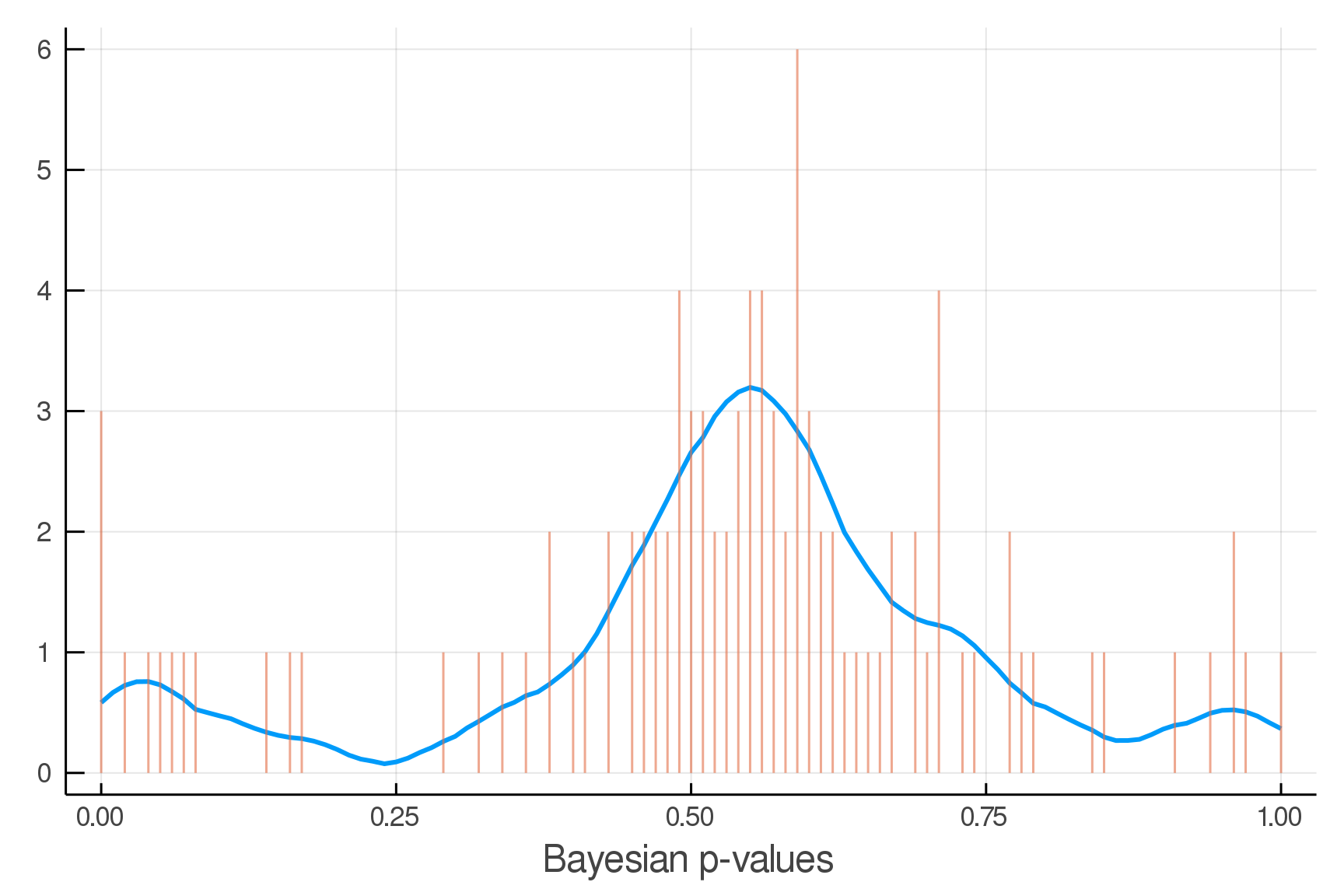
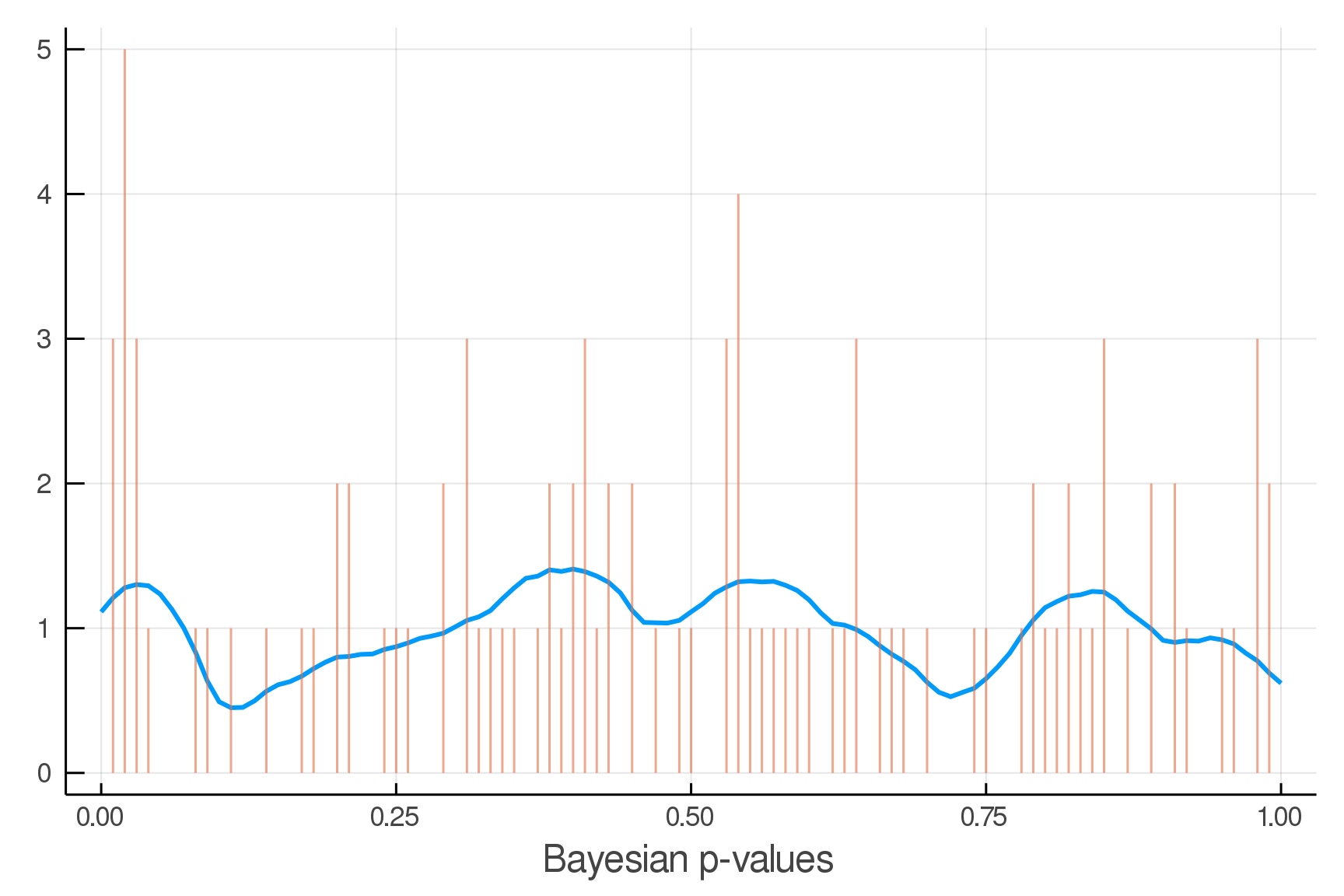
Posterior Predictive Checks

pvals = mean.(truth.y .> postpred.y)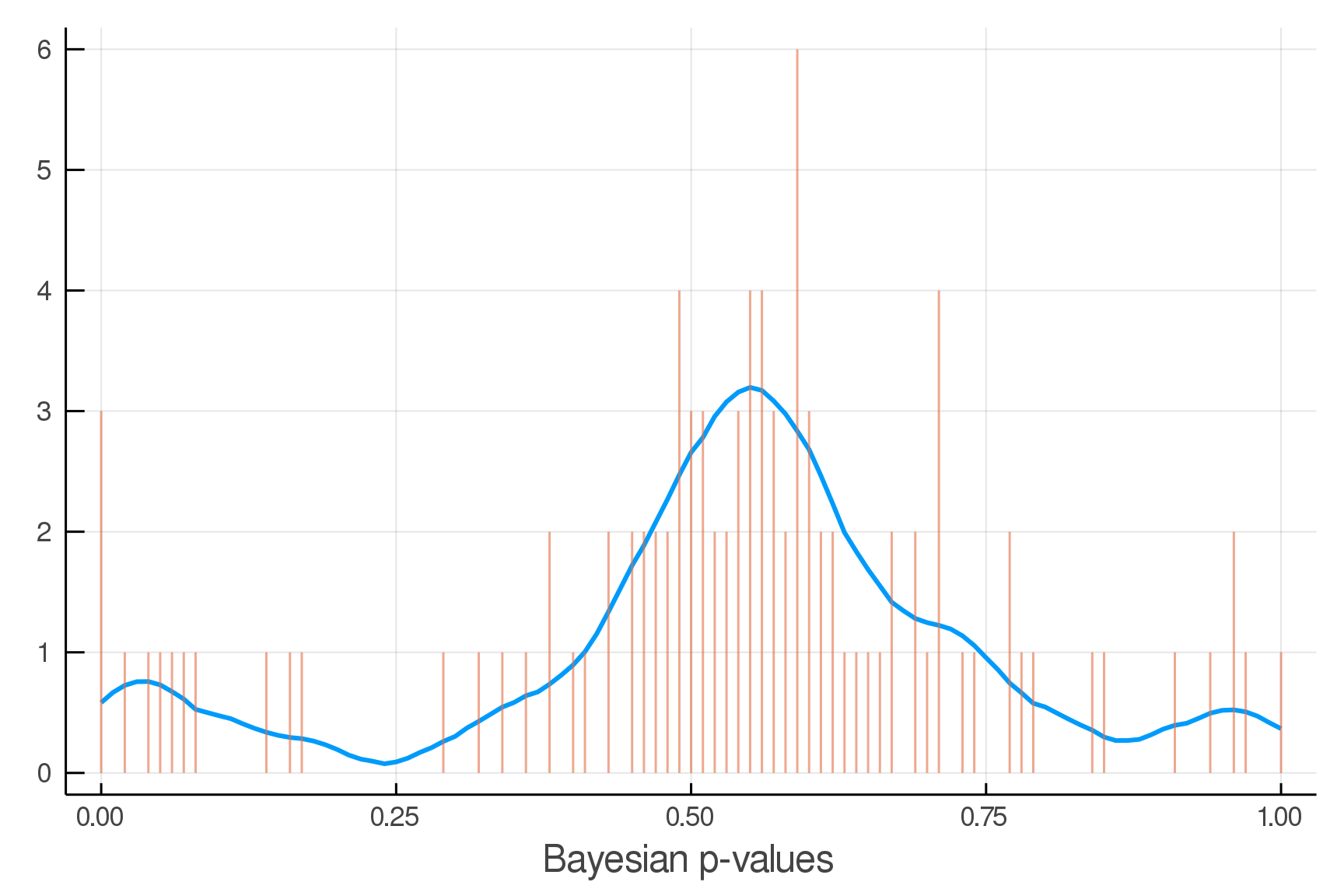

Where we expect the data

Where we see the data

Making it Robust

 m2 = @model x begin
     α ~ Normal()
     β ~ Normal()
     σ ~ HalfNormal()
     yhat = α .+ β .* x
     νinv ~ HalfNormal()
     ν = 1/νinv
     n = length(x)
     y ~ For(n) do j
             StudentT(ν,yhat[j],σ)
         end
 end

julia> post2 = dynamicHMC(m2(x=truth.x), (y=truth.y,)) |> particles
( σ = 0.57 ± 0.09, νinv = 0.609 ± 0.14
, β = 2.73 ± 0.073, α = 0.893 ± 0.077)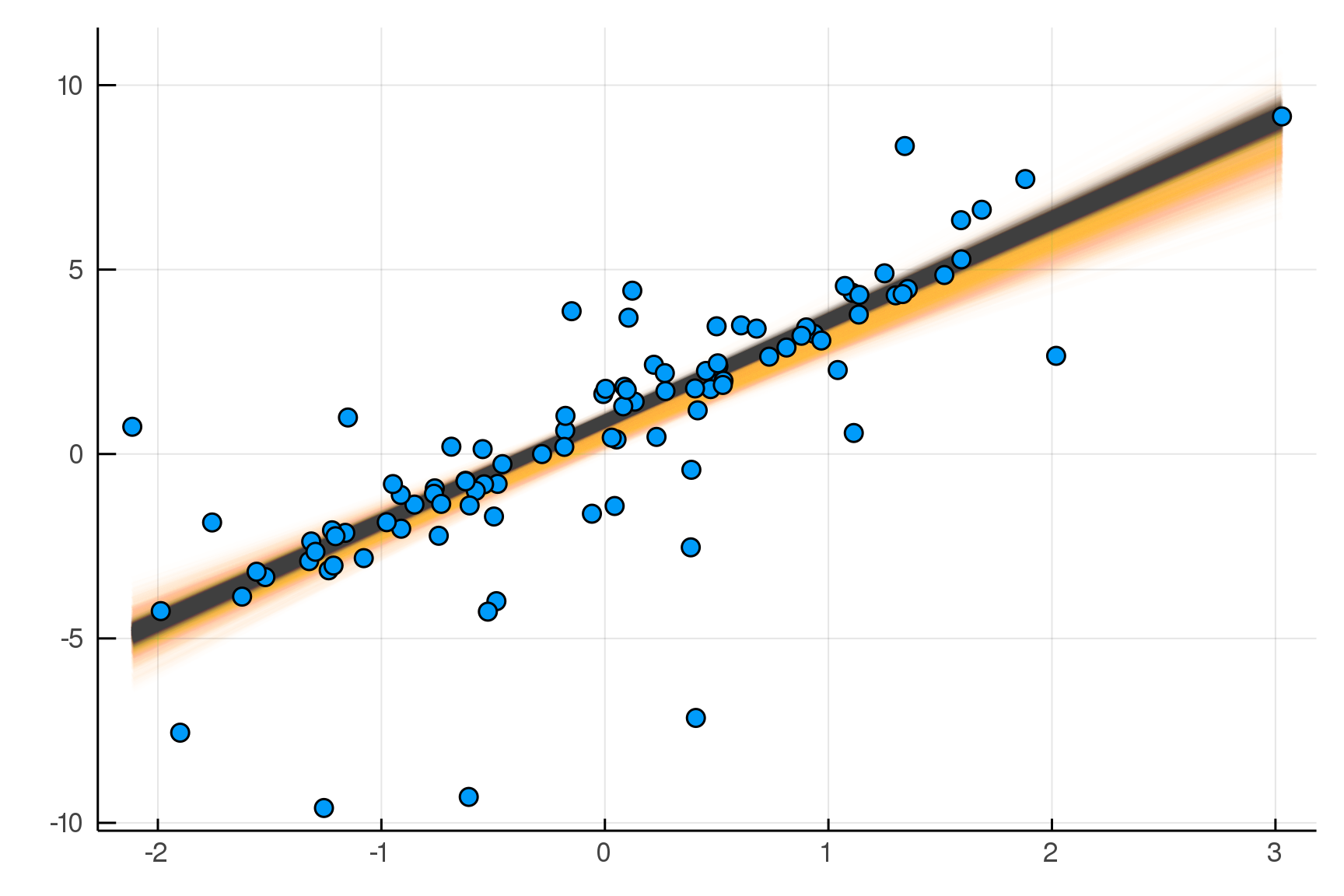

Updated Posterior Predictive Checks

Inference Primitive: rand

julia> Soss.sourceRand()(m)
quote
    σ = rand(HalfNormal())
    β = rand(Normal())
    α = rand(Normal())
    yhat = α .+ β .* x
    n = length(x)
    y = rand(For(((j,)->begin
                Normal(yhat[j], σ)
            end), n))
    (x = x, yhat = yhat, n = n
    , α = α, β = β, σ = σ, y = y)
end

@model x begin
    σ ~ HalfNormal()
    β ~ Normal()
    α ~ Normal()
    yhat = α .+ β .* x
    n = length(x)
    y ~ For(n) do j
        Normal(yhat[j], σ)
    end
end

Inference Primitive: logpdf

julia> Soss.sourceLogpdf()(m)
quote
    _ℓ = 0.0
    _ℓ += logpdf(HalfNormal(), σ)
    _ℓ += logpdf(Normal(), β)
    _ℓ += logpdf(Normal(), α)
    yhat = α .+ β .* x
    n = length(x)
    _ℓ += logpdf(For(n) do j
                Normal(yhat[j], σ)
            end, y)
    return _ℓ
end

@model x begin
    σ ~ HalfNormal()
    β ~ Normal()
    α ~ Normal()
    yhat = α .+ β .* x
    n = length(x)
    y ~ For(n) do j
        Normal(yhat[j], σ)
    end
end

Inference Primitive: symlogpdf

julia> Soss.sourceSymlogpdf()(m)
quote
    _ℓ = 0.0
    x = sympy.IndexedBase(:x)
    yhat = sympy.IndexedBase(:yhat)
    n = sympy.IndexedBase(:n)
    α = sympy.IndexedBase(:α)
    β = sympy.IndexedBase(:β)
    σ = sympy.IndexedBase(:σ)
    y = sympy.IndexedBase(:y)
    _ℓ += symlogpdf(HalfNormal(), σ)
    _ℓ += symlogpdf(Normal(), β)
    _ℓ += symlogpdf(Normal(), α)
    yhat = sympy.IndexedBase(:yhat)
    n = sympy.IndexedBase(:n)
    _ℓ += symlogpdf(For(n) do j
                Normal(yhat[j], σ)
            end, y)
    return _ℓ
end

@model x begin
    σ ~ HalfNormal()
    β ~ Normal()
    α ~ Normal()
    yhat = α .+ β .* x
    n = length(x)
    y ~ For(n) do j
        Normal(yhat[j], σ)
    end
end

Symbolic Simplification

julia> symlogpdf(m)

julia> symlogpdf(m) |> expandSums

-3.7-0.5α^{2}-0.5β^{2}-σ^{2}+\sum_{j_{1}=1}^{n}\left(-0.92-\logσ-\frac{0.5\left(y_{j_{1}}-\hat{y}_{j_{1}}\right)^{2}}{σ^{2}}\right)

-3.7-0.5α^{2}-0.5β^{2}-σ^{2}-0.92n-n\logσ-\frac{0.5}{\sigma^{2}}\sum_{j_{1}=1}^{n}\left(y_{j_{1}}-\hat{y}_{j_{1}}\right)^{2}

Code Generation

julia> symlogpdf(m()) |> expandSums |> foldConstants |> codegen
quote
    var"##add#643" = 0.0
    var"##add#643" += -3.6757541328186907
    var"##add#643" += begin
            var"##mul#644" = 1.0
            var"##mul#644" *= -0.5
            var"##mul#644" *= begin
                    var"##arg1#646" = α
                    var"##arg2#647" = 2
                    var"##symfunc#645" = (Soss._pow)(var"##arg1#646", var"##arg2#647")
                    var"##symfunc#645"
                end
            var"##mul#644"
        end
    var"##add#643" += begin
            var"##mul#648" = 1.0
            var"##mul#648" *= -0.5
            var"##mul#648" *= begin
                    var"##arg1#650" = β
                    var"##arg2#651" = 2
                    var"##symfunc#649" = (Soss._pow)(var"##arg1#650", var"##arg2#651")
                    var"##symfunc#649"
                end
            var"##mul#648"
        end
    var"##add#643" += begin
            var"##mul#652" = 1.0
            var"##mul#652" *= -1.0
            var"##mul#652" *= begin
                    var"##arg1#654" = σ
                    var"##arg2#655" = 2
                    var"##symfunc#653" = (Soss._pow)(var"##arg1#654", var"##arg2#655")
                    var"##symfunc#653"
                end
            var"##mul#652"
        end
    var"##add#643" += begin
            var"##mul#656" = 1.0
            var"##mul#656" *= -0.9189385332046727
            var"##mul#656" *= n
            var"##mul#656"
        end
    var"##add#643" += begin
            var"##mul#657" = 1.0
            var"##mul#657" *= -0.5
            var"##mul#657" *= begin
                    var"##arg1#659" = σ
                    var"##arg2#660" = -2
                    var"##symfunc#658" = (Soss._pow)(var"##arg1#659", var"##arg2#660")
                    var"##symfunc#658"
                end
            var"##mul#657" *= begin
                    let
                        var"##sum#661" = 0.0
                        begin
                            var"##lo#663" = 1
                            var"##hi#664" = n
                            @inbounds for _j1 = var"##lo#663":var"##hi#664"
                                    begin
                                        var"##Δsum#662" = begin
                                                var"##arg1#666" = begin
                                                        var"##add#668" = 0.0
                                                        var"##add#668" += begin
                                                                var"##mul#669" = 1.0
                                                                var"##mul#669" *= -1.0
                                                                var"##mul#669" *= begin
                                                                        var"##arg1#671" = yhat
                                                                        var"##arg2#672" = _j1
                                                                        var"##symfunc#670" = (getindex)(var"##arg1#671", var"##arg2#672")
                                                                        var"##symfunc#670"
                                                                    end
                                                                var"##mul#669"
                                                            end
                                                        var"##add#668" += begin
                                                                var"##arg1#674" = y
                                                                var"##arg2#675" = _j1
                                                                var"##symfunc#673" = (getindex)(var"##arg1#674", var"##arg2#675")
                                                                var"##symfunc#673"
                                                            end
                                                        var"##add#668"
                                                    end
                                                var"##arg2#667" = 2
                                                var"##symfunc#665" = (Soss._pow)(var"##arg1#666", var"##arg2#667")
                                                var"##symfunc#665"
                                            end
                                        var"##sum#661" += var"##Δsum#662"
                                    end
                                end
                        end
                        var"##sum#661"
                    end
                end
            var"##mul#657"
        end
    var"##add#643" += begin
            var"##mul#676" = 1.0
            var"##mul#676" *= -1.0
            var"##mul#676" *= n
            var"##mul#676" *= begin
                    var"##arg1#678" = σ
                    var"##symfunc#677" = (log)(var"##arg1#678")
                    var"##symfunc#677"
                end
            var"##mul#676"
        end
    var"##add#643"
end

julia> @btime logpdf($m(x=x), $truth)
1.911 μs (25 allocations: 1.42 KiB)
-901.7607073245318

julia> @btime logpdf($m(x=x), $truth, codegen)
144.671 ns (1 allocation: 896 bytes)
-903.4977930382969

Default

Code Generation

New feature, still in development
Speedup depends on lots of things

First-Class Models

julia> m = @model begin
           a ~ @model begin
               x ~ Normal()
           end
       end;

julia> rand(m())
(a = (x = -0.20051706307697828,),)

julia> m2 = @model anotherModel begin
           y ~ anotherModel
           z ~ anotherModel
           w ~ Normal(y.a.x / z.a.x, 1)
       end;

julia> rand(m2(anotherModel=m)).w
-1.822683102320004

Higher-order Model Example

m = @model Prior,x,σ begin
    β ~ Prior
    yhat = β .* x
    y ~ For(eachindex(x)) do j
        Normal(yhat[j], σ)
    end
end

Arguments

Body

Models are declarative and function-like
Input the arguments
Output everything (as a named tuple)

Suspiciously missing:

Which variables are observed?

Getting the DAG

m = @model Prior,x,σ begin
    β ~ Prior
    yhat = β .* x
    y ~ For(eachindex(x)) do j
        Normal(yhat[j], σ)
    end
end

julia> digraph(m).N     # forward
Dict{Symbol,Set{Symbol}} with 6 entries:
  :σ     => Set(Symbol[:y])
  :y     => Set(Symbol[])
  :yhat  => Set(Symbol[:y])
  :β     => Set(Symbol[:yhat])
  :Prior => Set(Symbol[:β])
  :x     => Set(Symbol[:y, :yhat])

julia> digraph(m).NN     # reverse
Dict{Symbol,Set{Symbol}} with 6 entries:
  :σ     => Set(Symbol[])
  :y     => Set(Symbol[:σ, :yhat, :x])
  :yhat  => Set(Symbol[:β, :x])
  :β     => Set(Symbol[:Prior])
  :Prior => Set(Symbol[])
  :x     => Set(Symbol[])

\beta

\hat{y}

\text{Prior}

\sigma

using Ed Scheinerman's SimpleWorld.jl

The Predictive Distribution

m = @model Prior,x,σ begin
    β ~ Prior
    yhat = β .* x
    y ~ For(eachindex(x)) do j
        Normal(yhat[j], σ)
    end
end

julia> pred = predictive(m, :β)
@model (x, σ, β) begin
    yhat = β .* x
    y ~ For(eachindex(x)) do j
        Normal(yhat[j], σ)
    end
end

\beta

\hat{y}

\text{Prior}

\sigma

julia> predictive(m, :yhat)
@model (x, σ, yhat) begin
    y ~ For(eachindex(x)) do j
        Normal(yhat[j], σ)
    end
end

using Taine Zhao's MLStyle.jl

Model Types

struct Model{Args, Body} 
    args  :: Vector{Symbol}
    vals  :: NamedTuple
    dists :: NamedTuple
    retn  :: Union{Nothing, Symbol, Expr}
end

using Taine Zhao's GeneralizedGenerated.jl

m = @model Prior,x,σ begin
    β ~ Prior
    yhat = β .* x
    y ~ For(eachindex(x)) do j
        Normal(yhat[j], σ)
    end
end

julia> typeof(m)
Model{
    NamedTuple{(:Prior, :x, :σ),T} 
        where T<:Tuple,
    begin
    	β ~ Prior
    	yhat = β .* x
    	y ~ For(eachindex(x)) do j
            Normal(yhat[j], σ)
        end
    end
}

Thanks to Taine Zhao for this improvement

Importance Sampling

p = @model begin
    α ~ Normal(1,1)
    β ~ Normal(α^2,1)
end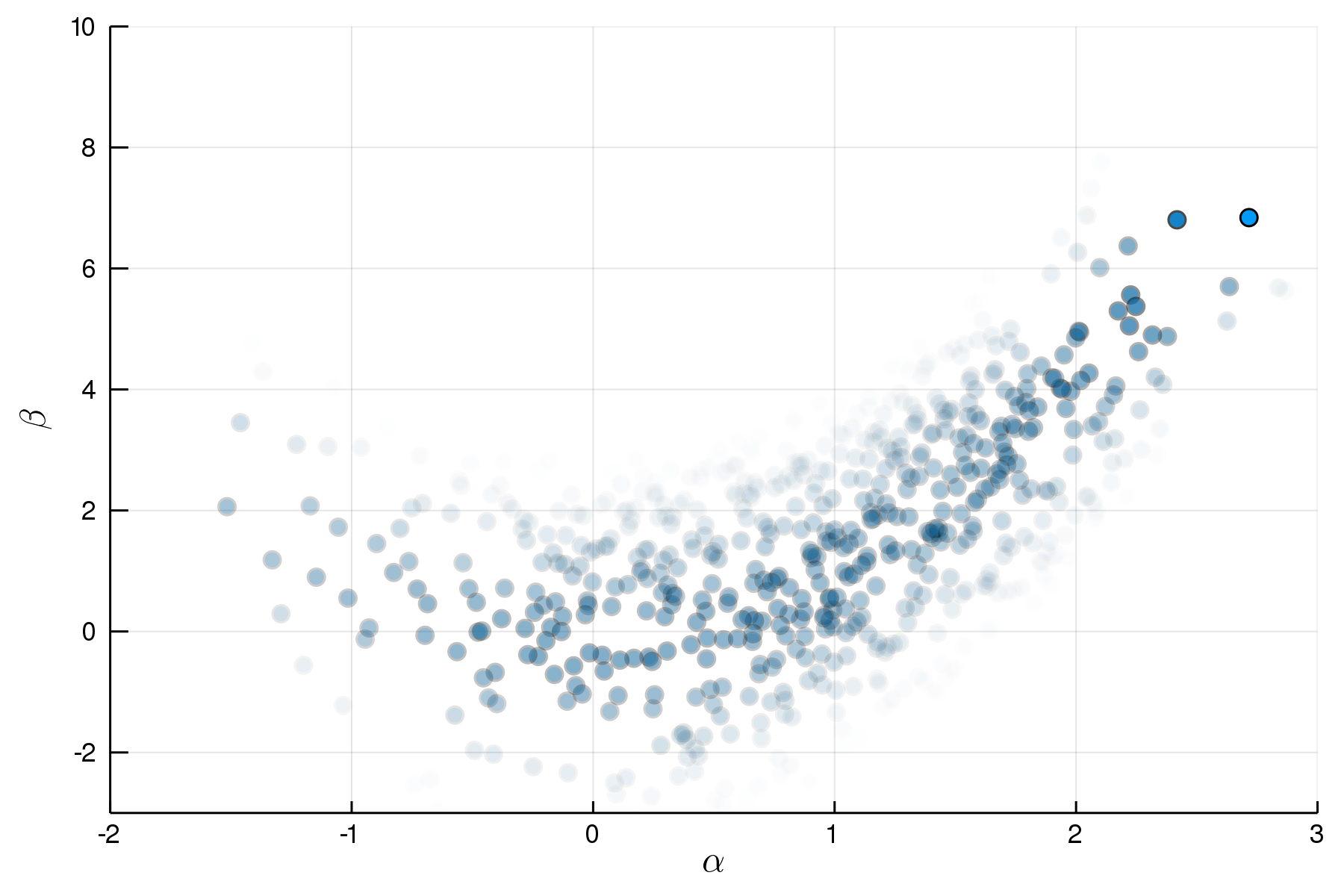

q = @model μα,σα,μβ,σβ begin
    α ~ Normal(μα,σα)
    β ~ Normal(μβ,σβ)
end

julia> sourceParticleImportance(p,q) 
:(function ##particlemportance#737(##N#736, pars)
      @unpack (μα, σα, μβ, σβ) = pars
      ℓ = 0.0 * Particles(##N#736, Uniform())
      α = Particles(##N#736, Normal(μα, σα))
      ℓ -= logpdf(Normal(μα, σα), α)
      β = Particles(##N#736, Normal(μβ, σβ))
      ℓ -= logpdf(Normal(μβ, σβ), β)
      ℓ += logpdf(Normal(1, 1), α)
      ℓ += logpdf(Normal(α ^ 2, 1), β)
      return (ℓ, (α = α, β = β))
  end)

=> Variational Inference

\ell(x) = \log p(x) - \log q(x)

\text{Sample } x \sim q\text{, then evaluate}

Hidden Markov Models, Step by Step

hmmStep = @model s0,step,noise begin
    s1 ~ EqualMix(step.(s0))
    y ~ noise(s1.x)
end;

julia> s0 = rand(Normal(0,10), 100);

julia> particles(s0)
Part100(0.4518 ± 9.93)

julia> rand(hmmStep(args)) |> pairs
pairs(::NamedTuple) with 5 entries:
  :s0    => [7.9962, -4.30039, 8.0346, -0.628184,  …  20.3864…]
  :step  => step
  :noise => noise
  :s1    => (s = 18.0924, ν = 2.0472, x = 16.8622)
  :y     => (s = 16.8622, y = 15.0147)

julia> dynamicHMC(hmmStep(args), (y=(y=1.0,),)) |> particles
(s1 = (ν = 5.48 ± 26.0, x = 0.792 ± 0.95),)

function step(s)
    m = @model s begin
        ν ~ HalfCauchy()
        x ~ StudentT(ν, s,1)
    end
    m(s=s)
end;

function noise(s)
    m = @model s begin
        y ~ Normal(s,1)
    end
    m(s=s)
end;

Thank You!

https://cscherrer.github.io/

https://github.com/cscherrer/Soss.jl

A Running Example

\begin{aligned} \text{Prior} &\in \mathbb{P}(\mathbb{R}) \\ x &\in \mathbb{R}^n \\ \sigma &\in \mathbb{R}_+ \\ \\ \beta &\sim \text{Prior} \\ \hat{y} &= \beta x \\ y &\sim \text{Normal}(\hat{y},\sigma) \end{aligned}

Build the model
Sample from generative model
Evaluate log density
Sample from posterior
Determine predictive distribution
Sample from posterior predictive distribution

Goals

Sampling from the Model

m = @model Prior,x,σ begin
    β ~ Prior
    yhat = β .* x
    y ~ For(eachindex(x)) do j
        Normal(yhat[j], σ)
    end
end

julia> Prior = Normal()
Normal{Float64}(μ=0.0, σ=1.0)

julia> args = (Prior=Prior, x=x, σ=2.0);

julia> truth = rand(m(args));

julia> pairs(truth)
pairs(::NamedTuple) with 6 entries:
  :Prior => Normal{Float64}(μ=0.0, σ=1.0)
  :x     => [-0.556027, -0.444383, 0.0271553]
  :σ     => 2.0
  :yhat  => [0.166521, 0.133086, -0.00813259]
  :β     => -0.299484
  :y     => [3.72224, -2.15672, -0.945344]

Joint Distributions

m = @model Prior,x,σ begin
    β ~ Prior
    yhat = β .* x
    y ~ For(eachindex(x)) do j
        Normal(yhat[j], σ)
    end
end

julia> pairs(args)
pairs(::NamedTuple) with 3 entries:
  :Prior => Normal{Float64}(μ=0.0, σ=1.0)
  :x     => [-0.556027, -0.444383, 0.0271553]
  :σ     => 2.0

julia> m(args)
Joint Distribution
    Bound arguments: [Prior, x, σ]
    Variables: [β, yhat, y]

@model (Prior, x, σ) begin
    β ~ Prior
    yhat = β .* x
    y ~ For(eachindex(x)) do j
        Normal(yhat[j], σ)
    end
end

Sampling from the Posterior

m = @model Prior,x,σ begin
    β ~ Prior
    yhat = β .* x
    y ~ For(eachindex(x)) do j
        Normal(yhat[j], σ)
    end
end

julia> pairs(args)
pairs(::NamedTuple) with 3 entries:
  :Prior => Normal{Float64}(μ=0.0, σ=1.0)
  :x     => [-0.556027, -0.444383, 0.0271553]
  :σ     => 2.0

julia> post = dynamicHMC(m(args), (y=truth.y,));

julia> particles(post)
(β = -0.181 ± 0.92,)

using Tamas Papp's DynamicHMC.jl

and Fredrik Bagge Carlson's MonteCarloMeasurements.jl

The Predictive Distribution

m = @model Prior,x,σ begin
    β ~ Prior
    yhat = β .* x
    y ~ For(eachindex(x)) do j
        Normal(yhat[j], σ)
    end
end

julia> argspost = merge(args, particles(post));

julia> pairs(argspost)
pairs(::NamedTuple) with 4 entries:
  :Prior => Normal{Float64}(μ=0.0, σ=1.0)
  :x     => [-0.556027, -0.444383, 0.0271553]
  :σ     => 2.0
  :β     => -0.18 ± 0.9

julia> pred = predictive(m, :β)
@model (x, σ, β) begin
    yhat = β .* x
    y ~ For(eachindex(x)) do j
        Normal(yhat[j], σ)
    end
end

The Predictive Distribution

m = @model Prior,x,σ begin
    β ~ Prior
    yhat = β .* x
    y ~ For(eachindex(x)) do j
        Normal(yhat[j], σ)
    end
end

julia> argspost = merge(args, particles(post));

julia> pairs(argspost)
pairs(::NamedTuple) with 4 entries:
  :Prior => Normal{Float64}(μ=0.0, σ=1.0)
  :x     => [-0.556027, -0.444383, 0.0271553]
  :σ     => 2.0
  :β     => -0.18 ± 0.9

julia> postpred = pred(argspost) |> rand;

julia> pairs(postpred)
pairs(::NamedTuple) with 5 entries:
  :x    => [-0.556027, -0.444383, 0.0271553]
  :σ    => 2.0
  :β    => -0.18 ± 0.9
  :yhat => [0.1 ± 0.5, 0.0801 ± 0.4, -0.0049 ± 0.024]
  :y    => [-5.18 ± 0.5, 2.09 ± 0.4, 2.16 ± 0.024]

julia> pred = predictive(m, :β)
@model (x, σ, β) begin
    yhat = β .* x
    y ~ For(eachindex(x)) do j
        Normal(yhat[j], σ)
    end
end

Under the Hood

Canonical Representation

m = @model Prior,x,σ begin
    β ~ Prior
    yhat = β .* x
    y ~ For(eachindex(x)) do j
        Normal(yhat[j], σ)
    end
end

julia> canonical(m)
@model (Prior, x, σ) begin
    β ~ Prior
    yhat = β .* x
    y ~ For(((j,)->begin
            Normal(yhat[j], σ)
        end), (eachindex(x),))
end

"There's more than one way to do it" 👍
Syntax → Semantics map is not faithful 👎
Solution: Standardize AST before processing

Inference Primitive: rand

julia> Soss.sourceRand()(m)
quote
    β = rand(Prior)
    yhat = β .* x
    y = rand(For(((j,)->begin
            Normal(yhat[j], σ)
        end), 
        (eachindex(x),)))
    (Prior = Prior, x = x, σ = σ,
    yhat = yhat, β = β, y = y)
end

m = @model Prior,x,σ begin
    β ~ Prior
    yhat = β .* x
    y ~ For(eachindex(x)) do j
        Normal(yhat[j], σ)
    end
end

Inference Primitive: logpdf

julia> Soss.sourceLogpdf()(m)
quote
    _ℓ = 0.0
    _ℓ += logpdf(Prior, β)
    yhat = β .* x
    _ℓ += logpdf(For(eachindex(x)) do j
            Normal(yhat[j], σ)
        end, y)
    return _ℓ
end

m = @model Prior,x,σ begin
    β ~ Prior
    yhat = β .* x
    y ~ For(eachindex(x)) do j
        Normal(yhat[j], σ)
    end
end

Inference Primitive: weightedSample

julia> Soss.sourceWeightedSample((y=truth.y,))(m)
quote
    _ℓ = 0.0
    β = rand(Prior)
    yhat = β .* x
    _ℓ += logpdf(For(eachindex(x)) do j
        Normal(yhat[j], σ)
    end, y)
    return (_ℓ, 
        (Prior = Prior, x = x, σ = σ, 
            yhat = yhat, β = β, y = y)
    )
end

m = @model Prior,x,σ begin
    β ~ Prior
    yhat = β .* x
    y ~ For(eachindex(x)) do j
        Normal(yhat[j], σ)
    end
end

Inference Primitive: xform

m = @model Prior,x,σ begin
    β ~ Prior
    yhat = β .* x
    y ~ For(eachindex(x)) do j
        Normal(yhat[j], σ)
    end
end

julia> xform(jd1, (y=truth.y,))
TransformVariables.TransformTuple{
    NamedTuple{(:β,),Tuple{TransformVariables.Identity}}
}((β = asℝ,), 1)

julia> xform(jd2, (y=truth.y,))
TransformVariables.TransformTuple{
    NamedTuple{(:β,),Tuple{TransformVariables.ShiftedExp{true,Float64}}}
}((β = asℝ₊,), 1)

julia> jd1 = m(Prior=Normal(), x=x, σ=2.0);

julia> jd2 = m(Prior=Exponential(), x=x, σ=2.0);

Soss: Lightweight Probabilistic Programming in Julia

Chad Scherrer

June 16, 2023

Making Rational Decisions

Managed Uncertainty

Rational Decisions

Bayesian Analysis

Probabilistic Programming

Risk

Custom models

The Two-Language Problem

Python

C

Deep Learning Framework

Introducing Soss

A (Very) Simple Example

Theory

Soss

Building a Linear Model

Building a Linear Model

Sampling from the Posterior Distribution

The Posterior Predictive Distribution

Start with Data

Sample Parameters|Data

Sample Data|Parameters

Real Data

Replicated Fake Data

The Posterior Predictive Distribution

Posterior Predictive Checks

Making it Robust

Updated Posterior Predictive Checks

Inference Primitive: rand

Inference Primitive: logpdf

Inference Primitive: symlogpdf

Symbolic Simplification

Code Generation

First-Class Models

Higher-order Model Example

Getting the DAG

The Predictive Distribution

Model Types

Importance Sampling

Hidden Markov Models, Step by Step

Thank You!

A Running Example

Goals

Sampling from the Model

Joint Distributions

Sampling from the Posterior

The Predictive Distribution

The Predictive Distribution

Under the Hood

Canonical Representation

Inference Primitive: rand

Inference Primitive: logpdf

Inference Primitive: weightedSample

Inference Primitive: xform

Copy of 2023-03-Basis-LabMeeting

More from Chad Scherrer