Deep Implicits
with Differential Rendering
Daniel Yukimura

Goals for today:
- Differentiable Volumetric Rendering
- Implicit Differentiable Rendering
- Discussion
Differentiable Volumetric Rendering


Occupancy Network
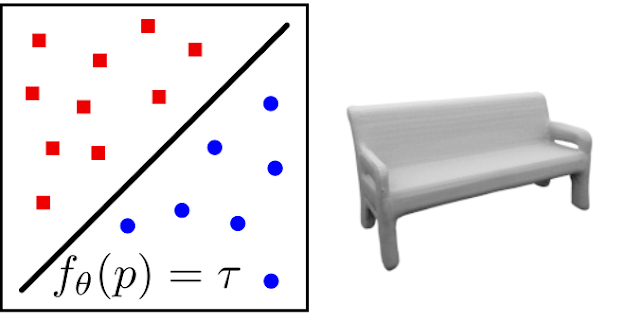
f_\theta: \mathbb{R}^3 \times \mathcal{Z} \rightarrow [0,1]
Real-world scenarios

Can we infer implicit 3D representations without 3D supervision?
Architecture

- Volumetric Rendering is differentiable here!
- Depth gradients
Forward Pass - Rendering:
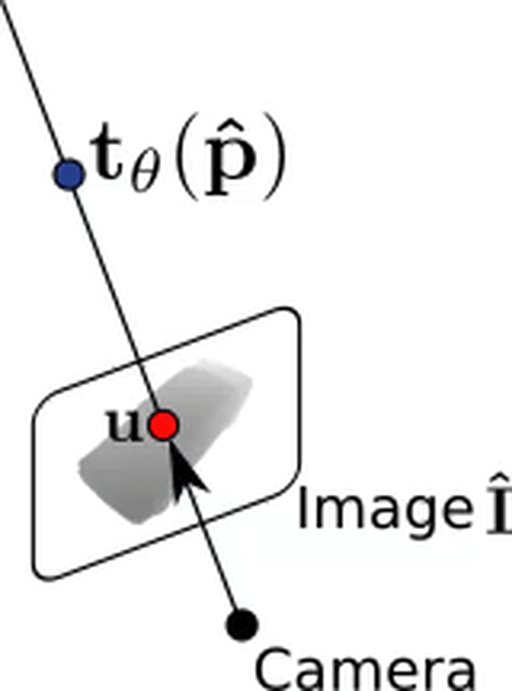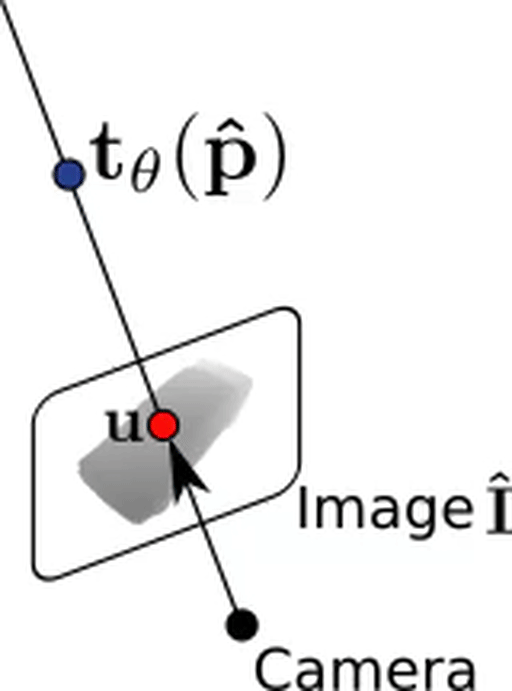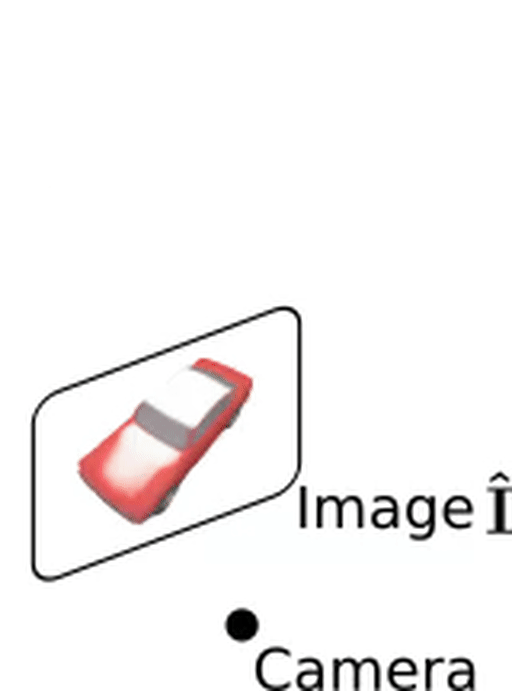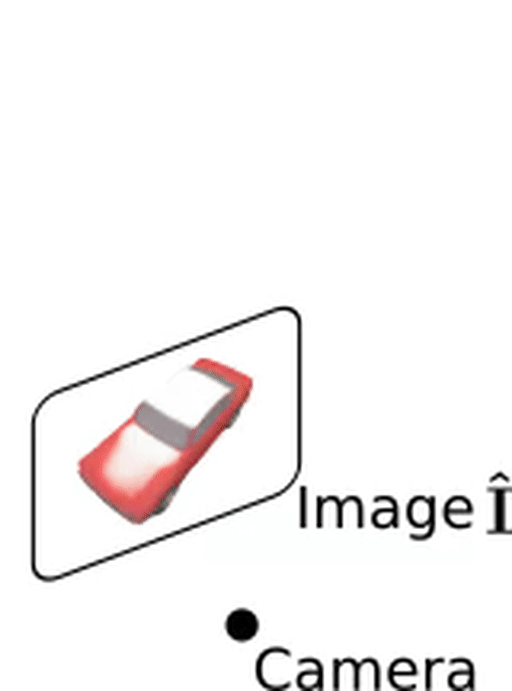
Texture mapping:
t_\theta: \mathbb{R}^3 \times \mathcal{Z} \rightarrow \mathbb{R}^3
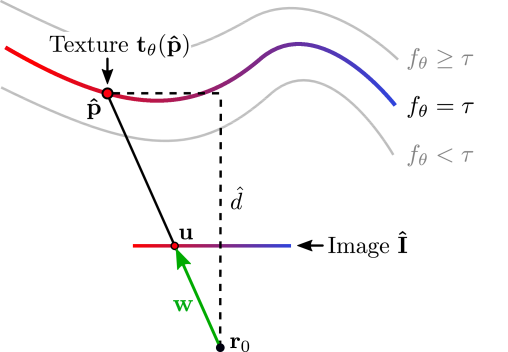

\hat{p} = \text{``first interesection with } \{p\in \mathbb{R}^3 | f_\theta(p) = \tau \} \text{"}
\mathcal{L}(\hat{I}, I) = \sum\limits_u \|\hat{I}_u - I_u \|
Loss:
Differentiable Rendering:
\frac{\partial \mathcal{L}}{\partial\theta} = \sum\limits_u \frac{\partial \mathcal{L}}{\partial \hat{I}_u} \frac{\partial \hat{I}_u}{\partial \theta} \\
= \sum\limits_u \frac{\partial \mathcal{L}}{\partial \hat{I}_u} \frac{\partial t_\theta (\hat{p})}{\partial \theta} \frac{\partial \hat{p}}{\partial\theta}
KNOWN
??
Depth Gradients:
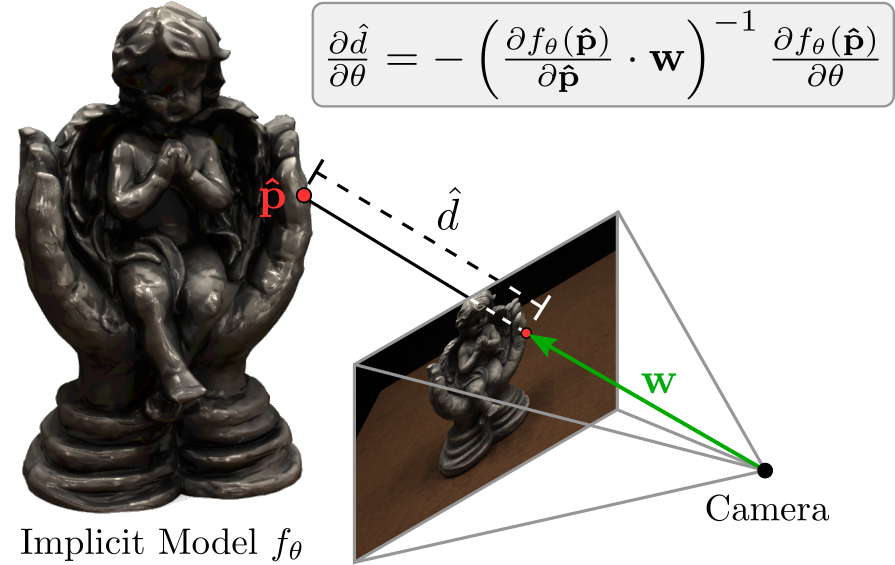
r(d) = r_0 + d w
\exists \hat{d} \text{ s.t. } \hat{p} = r(\hat{d})
Results



Results
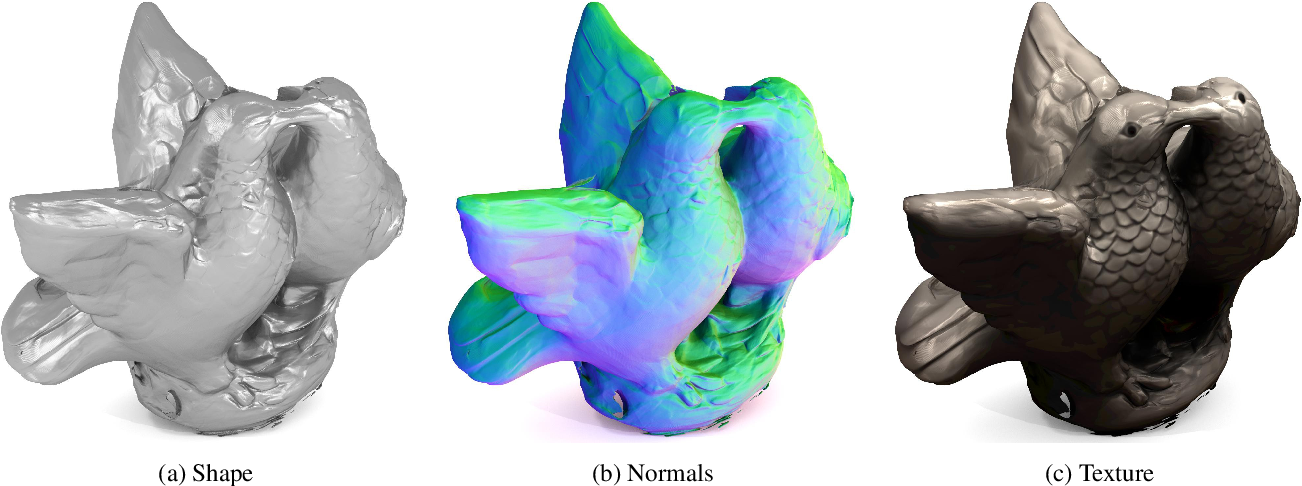
Implicit Differentiable Rendering
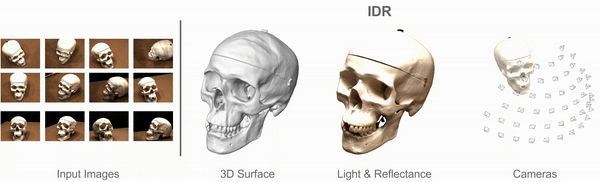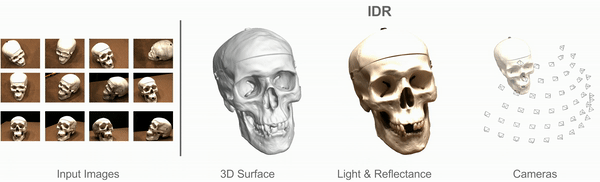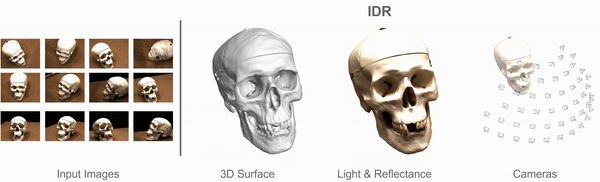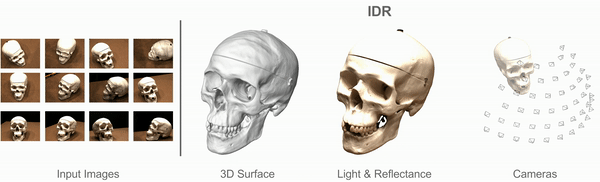
Multiview 3D Surface Reconstruction
Input: Collection of 2D images (masked)
with rough or noisy camera info.
Targets:
- Geometry
- Appearance (BRDF, lighting conditions)
- Cameras
Method:
Geometry:
\mathcal{S}_\theta = \{ x\in \mathbb{R}^3 | f(x;\theta) = 0 \}
signed distance function (SDF) +
implicit geometric regularization (IGR)

\theta
- geometry parameters
IDR - Forward pass
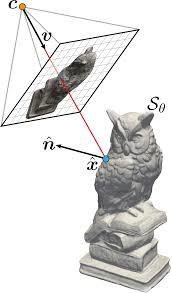
R_p(\tau) = \{ c_p + t v_p | t \geq 0 \}
\hat{x}_p = \hat{x}_p(\theta, \tau) = R_p(\tau) \cap \mathcal{S}_\theta
\tau
- camera parameters
Ray cast:
(first intersection)
IDR - Forward pass

L_p(\theta, \gamma, \tau) = M(\hat{x}_p, \hat{n}_p, \hat{z}_p, v_p; \gamma)
\gamma
- appearance parameters
Output (Light Field):
Surface normal
\hat{n}_p(\theta)
Global gometry feature vector
\hat{z}_p(\hat{x}_p; \theta)
Differentiable intersections
\theta_0, \tau_0 - \text{current parameters}
\hat{x}(\theta, \tau) = c + t_0 v - \frac{v}{\nabla_x f(x_0; \theta_0) \cdot v_0} f(c + t_0 v; \theta)
Lemma:
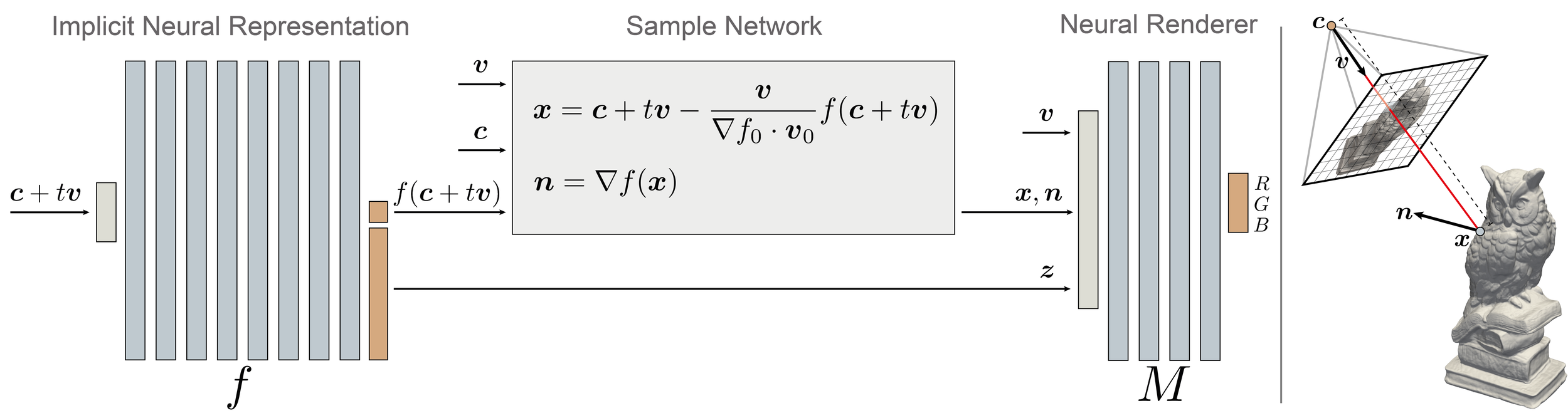
Light Field Approx.
L(\hat{x}, w^o) = L^e(\hat{x}, w^o) + \int\limits_\Omega B(\hat{x}, \hat{n}, w^i, w^o) L^i (\hat{x}, w^i) (\hat{n}\cdot w^i) d w^i
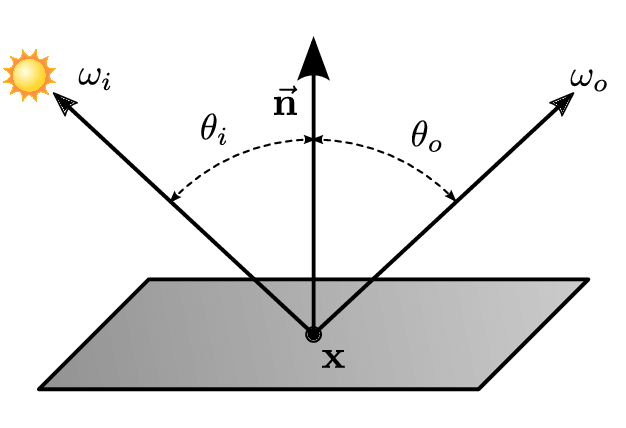
BRDF function
out direction
income direction
emitted
radiance
incoming radiance
= M_0(\hat{x}, \hat{n}, v)
L(\theta, \gamma, \tau) = M(\hat{x}, \hat{n}, v; \gamma)
Results:


Deep Implicits
By Daniel Yukimura
Deep Implicits
- 346



