Differentiable Rendering
Daniel Yukimura
scene
parameters
2D image
- camera pose
- geometry
- materials
- lighting
- ...
rendering
scene
parameters
2D image
rendering
rendering
differentiable
Feedback
Learning
- Inverse Graphics
- Optimization
- 3D Reconstruction
- Fast rendering
- ...
Applications:
Wang Yifan, Felice Serena, Shihao Wu, Cengiz Öztireli, Olga Sorkine-Hornung - ACM SIGGRAPH ASIA 2019.
Sameer Agarwal, Noah Snavely, Ian Simon, Steven M. Seitz and Richard Szeliski - International Conference on Computer Vision, 2009, Kyoto, Japan.
Differentiable Monte Carlo Ray Tracing through Edge Sampling
L_o(x, \vec \omega) = L_e(x, \vec \omega) + \displaystyle\int_{\Omega} L_i(x,\vec \omega')f_r(\vec \omega, x, \vec \omega') \cos(\theta) d\vec\omega'
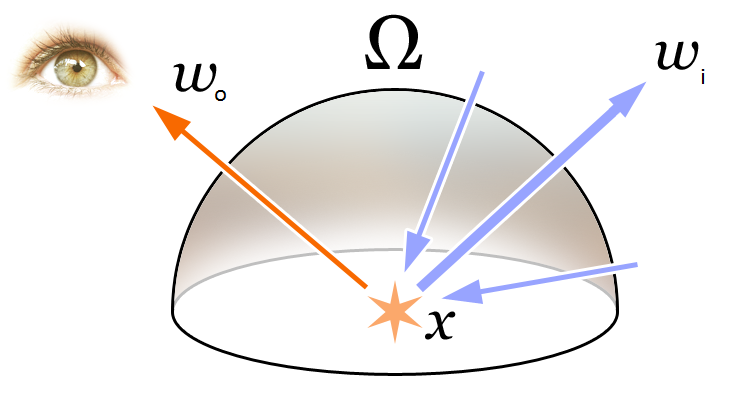
Rendering equation:
Global Illumination
(Recalling)
Monte Carlo Integration
(Recalling)
\displaystyle\int f(x) dx = ?
\mathbb{E}\left[f(X)\right] = \displaystyle\int f(x) p(x) dx
\approx \frac{1}{N} \sum\limits_{i=1}^N f(X_i)
\text{(LLN)}
X_i \sim p(\cdot)
\displaystyle\int f(x) dx = \displaystyle\int f(x)\frac{p(x)}{p(x)} dx
= \mathbb{E}\left[ \frac{f(X)}{p(X)} \right]
\approx \frac{1}{N} \sum\limits_{i=1}^N \frac{f(X_i)}{p(X_i)}
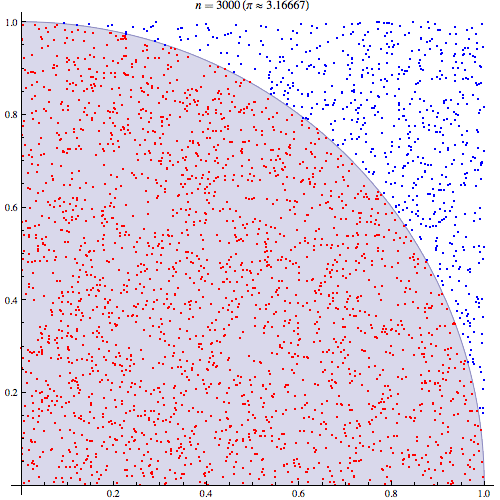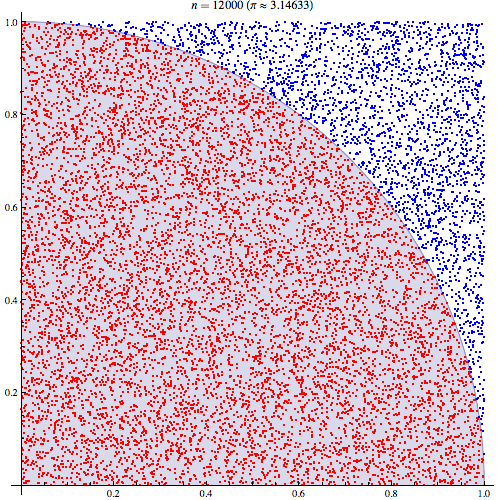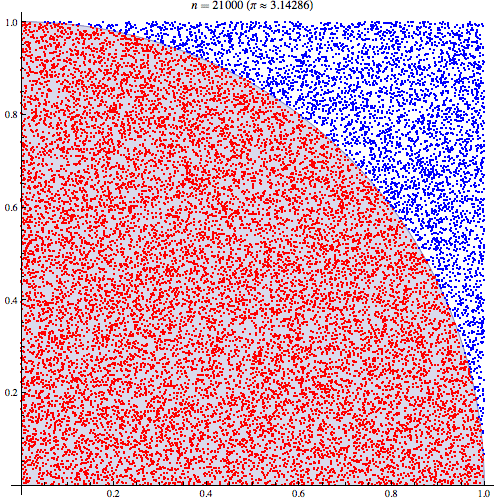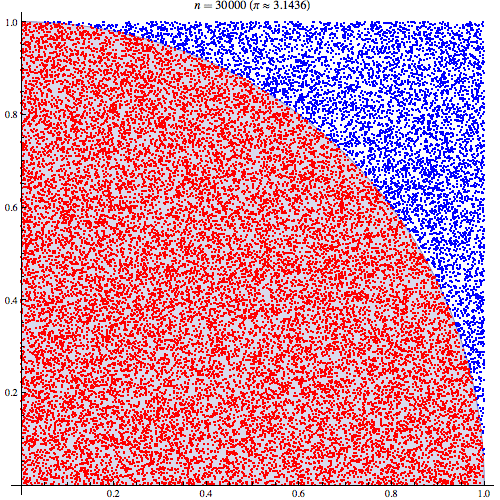
Monte Carlo Integration
(Recalling)
\displaystyle\int_{\Omega} L_i(x,\vec \omega')f_r(\vec \omega, x, \vec \omega') \cos(\theta) d\vec\omega' \approx \frac{1}{N}\sum\limits_{i=1}^N \dfrac{L_i(x,\vec \omega_i')f_r(\vec \omega, x, \vec \omega_i') \cos(\theta) d\vec\omega_i'}{p(\vec\omega_i')}
Path Tracing
(Recalling)
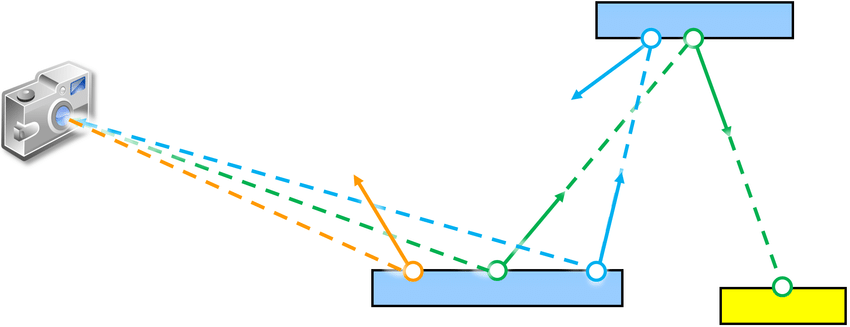
Differentiable Monte Carlo Ray Tracing through Edge Sampling
\text{Parameter set } \Phi
- camera pose
- geometry
- materials
- lighting
- ...
\text{Path Tracing}
I
f(I)
\text{(image)}
\text{scalar function}\\
\text{e.g. loss function}
\text{Goal: Differentiate/Backpropagate}
Strategy: Break into smooth and discontinuous regions.
L_i(p) = \displaystyle\int_{\mathcal{M}} {\ell_i( p \leftarrow m ) d A(m)}
= (S_i) + (D_i)
S_i \rightarrow \text{tradicional area sampling }
+ \text{ auto-differentiation}
D_i \rightarrow \text{Edge Sampling}
Assumptions:
- triangular meshes (with no interpenetration)
- no point light sources
- no perfectly specular surfaces
Primary visibility
(2D screen-space domain)
I = \displaystyle\int \hspace{-1mm}\displaystyle\int k(x,y) L(x,y) dx dy
\text{pixel color}
\text{pixel filter}
\text{radiance}
f(x,y) = k(x,y) L(x,y)
\textbf{Goal: } \nabla I = \nabla \displaystyle\int \hspace{-1mm}\displaystyle\int f(x,y;\Phi) dx dy
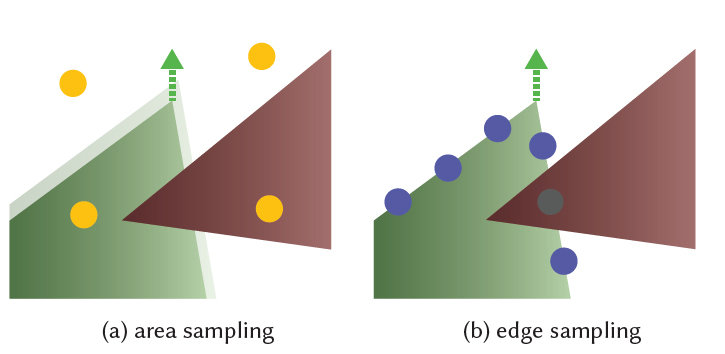
- All discontinuities happen at triangle edges.
\bullet \hspace{2mm} \text{From an edge split the space in two: } f_u \text{ and } f_\ell
\alpha(x,y) > 0 \Rightarrow (x,y)\in f_u
\text{edge equation}
f(x,y) = \theta( \alpha(x,y) ) f_u(x, y) + \theta( -\alpha(x,y) ) f_\ell(x,y)
\text{step function}
\text{edge: } (a_x, a_y), (b_x, b_y)
\alpha(x,y) = (a_y - b_y)x + (b_x - a_x)y + (a_x b_y - b_x a_y)
f(x,y) = \displaystyle\sum\limits_{i} \theta( \alpha_i(x,y) ) f_i(x, y)
\nabla \displaystyle\int \hspace{-2mm}\displaystyle\int \theta( \alpha_i(x,y) ) f_i(x, y) d_x d_y = \displaystyle\int \hspace{-2mm}\displaystyle\int \theta(\alpha_i(x,y)) \nabla f_i(x,y) dx dy
+ \displaystyle\int \hspace{-2mm}\displaystyle\int \delta(\alpha_i(x,y)) \nabla \alpha_i(x,y) f_i(x,y) dx dy
\textbf{discontinuous}
\textbf{smooth}
\displaystyle\int \hspace{-2mm}\displaystyle\int \delta(\alpha_i(x,y)) \nabla \alpha_i(x,y) f_i(x,y) dx dy =
= \displaystyle\int \hspace{-4mm}\displaystyle\int\limits_{\alpha_i(x,y)=0} \dfrac{\nabla \alpha_i(x,y)}{\|\nabla_{x,y} \alpha_i(x,y)\|} \nabla \alpha_i(x,y) f_i(x,y) d\sigma (x,y)
\text{length measure}\\ \text{on the edge}
\displaystyle\int \hspace{-4mm}\displaystyle\int\limits_{\alpha_i(x,y)=0} \dfrac{\nabla \alpha_i(x,y)}{\|\nabla_{x,y} \alpha_i(x,y)\|} \nabla \alpha_i(x,y) f_i(x,y) d\sigma (x,y)
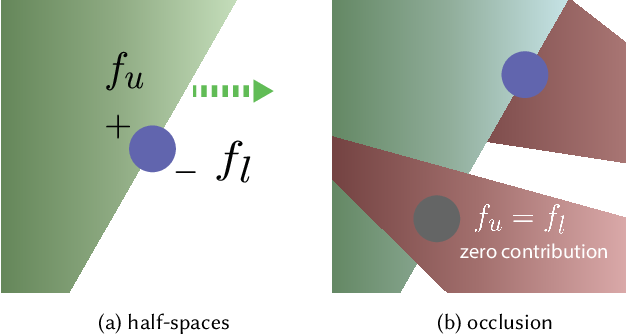
Monte Carlo estimation:
\approx \dfrac{1}{N} \displaystyle\sum\limits_{j=1}^N \dfrac{\|E\| \nabla \alpha_i(x_j,y_j) (f_u(x_j,y_j) - f_\ell(x_j, y_j)) }{ P(E) \|\nabla_{x,y} \alpha_i(x,y)\|}
\text{length of E}
\text{prob. of selec. E}
Secondary visibility
g(p) = \displaystyle \int_\mathcal{M} h(p, m) dA(m)
(global illumination - 3D)
\text{scene manifold}
\text{area measure}
\text{3D edge: } (v_0, v_1)
\theta( \alpha(p,m) ) h_u(p,m) + \theta( -\alpha(p,m) ) h_\ell(p,m)
\alpha(p, m) = (m - p)\cdot (v_0 - p) \times (v_1 - p)
\alpha(p, m) = (m - p)\cdot (v_0 - p) \times (v_1 - p)
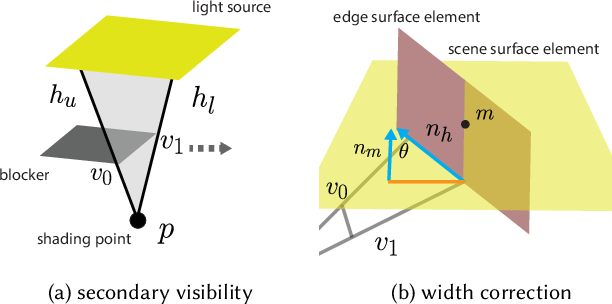
edge portion:
\displaystyle \int\limits_{\alpha(p,m) = 0} \dfrac{\nabla \alpha(p,m)}{\|\nabla_m \alpha(p,m)\|} h(p,m) \dfrac{1}{\|n_m \times n_h\|} d\sigma' (m)
n_h = \dfrac{(v_0 - p)\times (v_1 - p)}{\|(v_0 - p)\times (v_1 - p)\|}
Importance Sampling The Edges
- There are many triangles to sample.
- Now we have to sample edges
- and sample points from the edges...
- Most edges are not silhouette
- not all points have non-zero contribution
Hierarchical edge sampling
two hierarchies:
- Triangle edges that associate with only one face and meshes w/ no smooth shading.
- All the remaining edges
volume hierarchie:
- 3D bounding volume: 3D pos. of edge endpoints.
- 6D bounding volume: pos. of edge endpoints and the normals associated w/ the faces of the edge
Importance sampling a single edge
- Sample based on the BRDF
- Precompute a table of fitted linearly transformed cosines for all BRDFs.
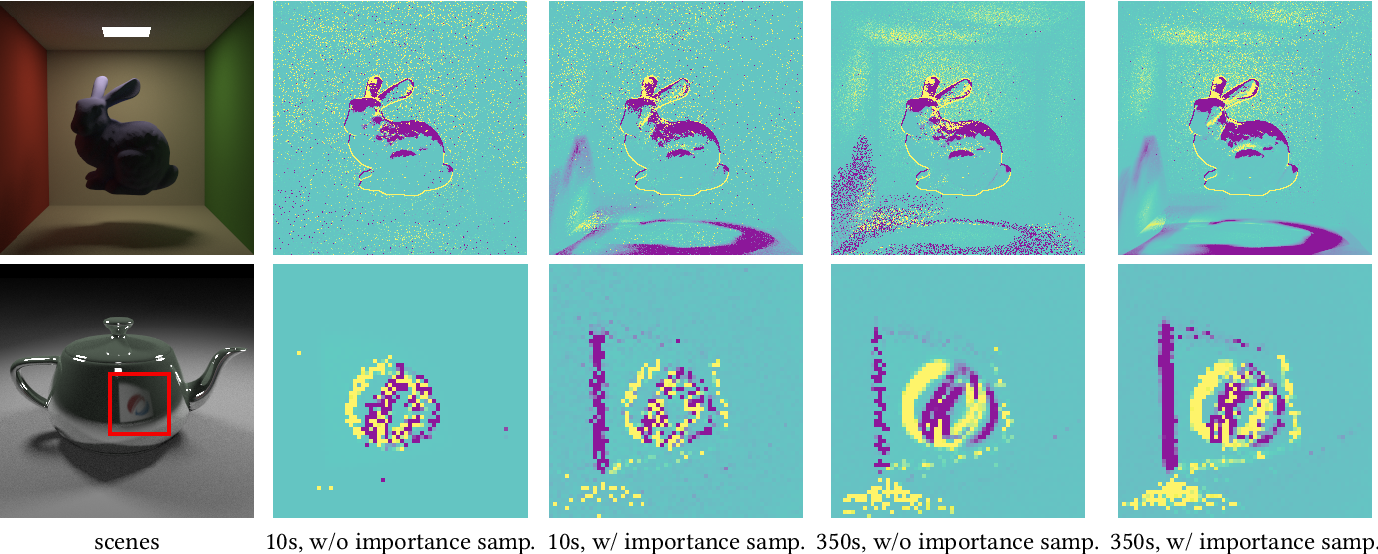
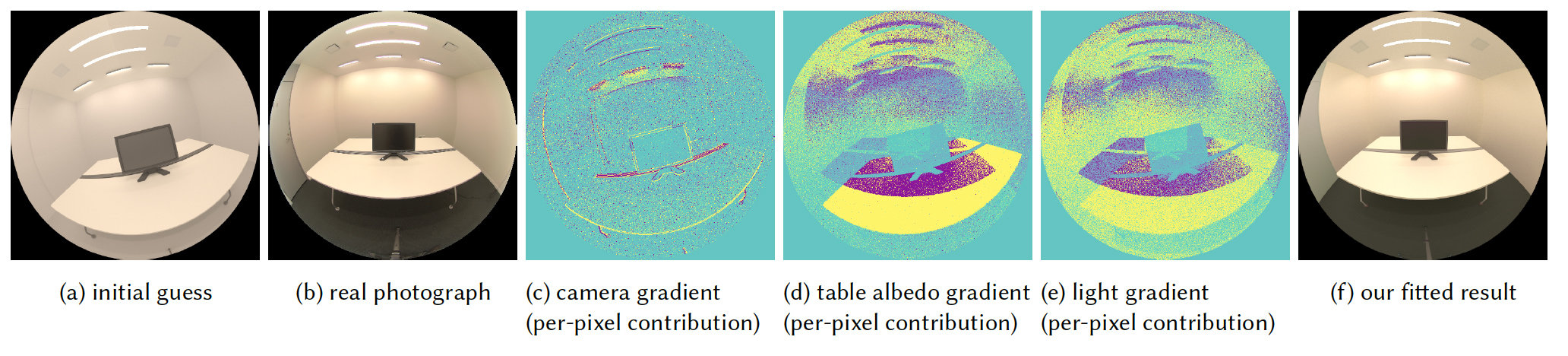
Results
Inverse rendering:
Adversarial examples:
Implicit Representation
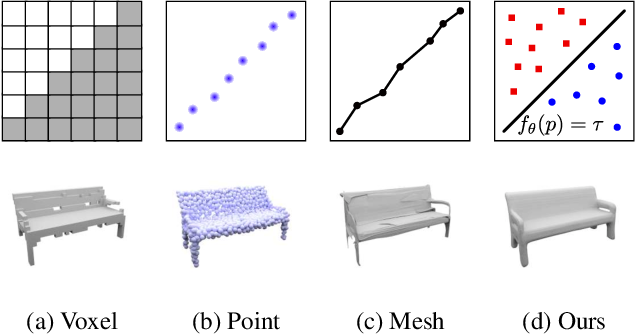
- Do not represent 3D shape explicitly
- Instead, consider it implicitly as decision boundary of a classifier
Occupancy networks
- Represent the implicit surface as a neural network.
f_\theta: \mathbb{R}^3 \times \mathcal{Z} \rightarrow [0,1]
\text{3D location}
\text{Condition}
\text{occupancy}\\ \text{probability}
Differentiable Volumetric Rendering
Architecture
- Volumetric Rendering is differentiable here!
- Depth gradients
Forward Pass - Rendering:
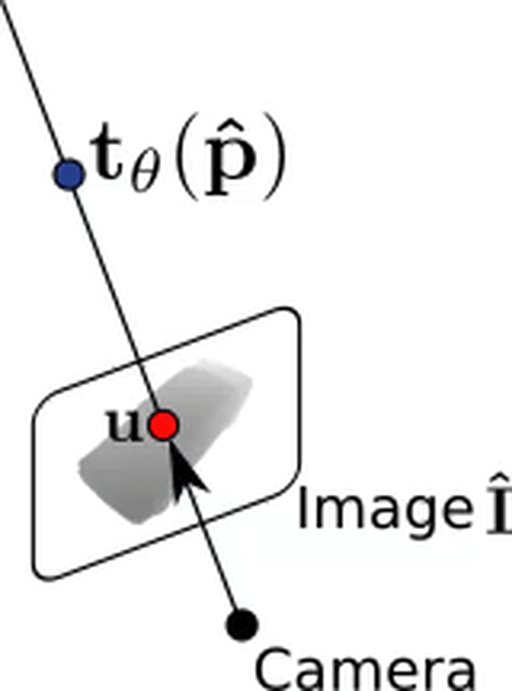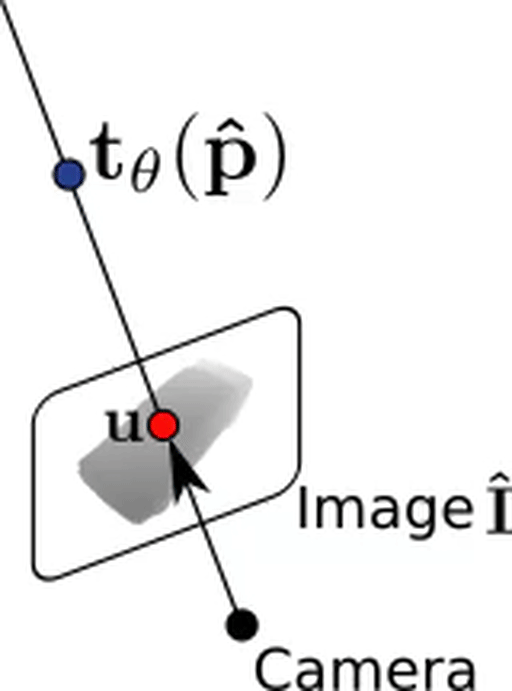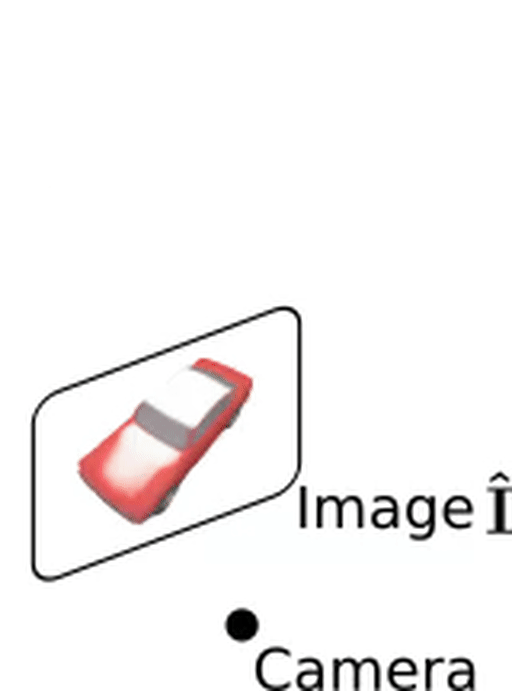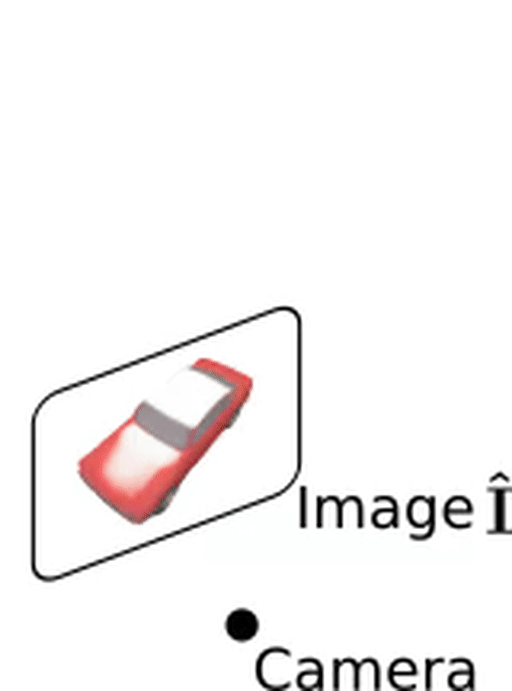
Texture mapping:
t_\theta: \mathbb{R}^3 \times \mathcal{Z} \rightarrow \mathbb{R}^3
\hat{p} = \text{``first interesection with } \{p\in \mathbb{R}^3 | f_\theta(p) = \tau \} \text{"}
\mathcal{L}(\hat{I}, I) = \sum\limits_u \|\hat{I}_u - I_u \|
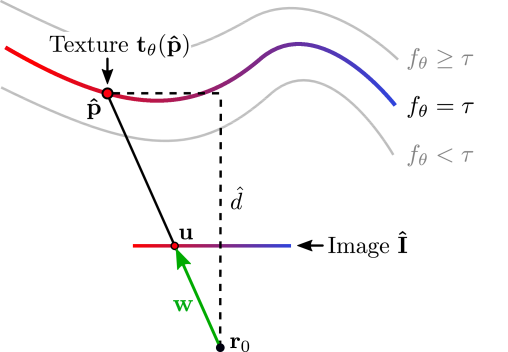
Loss:
Differentiable Rendering:
\frac{\partial \mathcal{L}}{\partial\theta} = \sum\limits_u \frac{\partial \mathcal{L}}{\partial \hat{I}_u} \frac{\partial \hat{I}_u}{\partial \theta} \\
= \sum\limits_u \frac{\partial \mathcal{L}}{\partial \hat{I}_u} \frac{\partial t_\theta (\hat{p})}{\partial \theta} \frac{\partial \hat{p}}{\partial\theta}
KNOWN
??
Depth Gradients:
r(d) = r_0 + d w
\exists\hspace{2mm} \hat{d} \text{ s.t. } \hat{p} = r(\hat{d})
\text{depth}
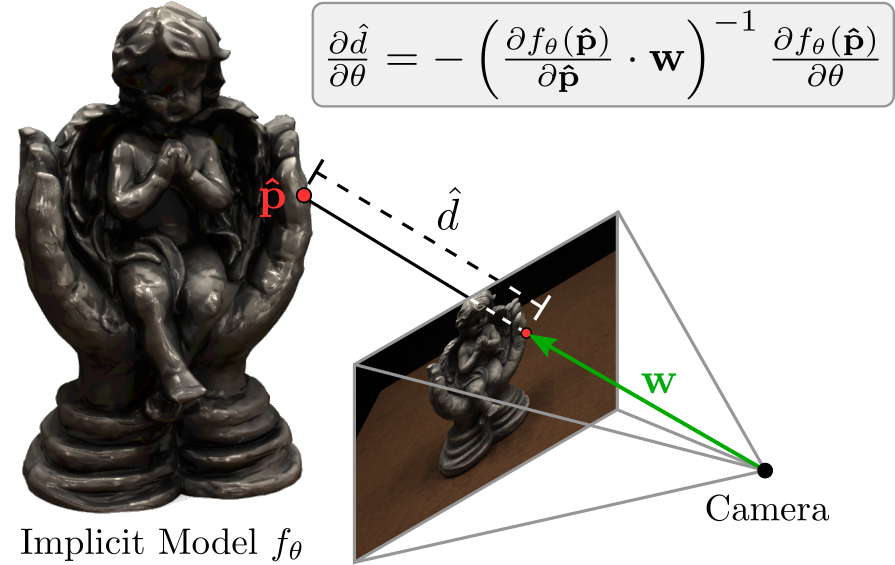
Results
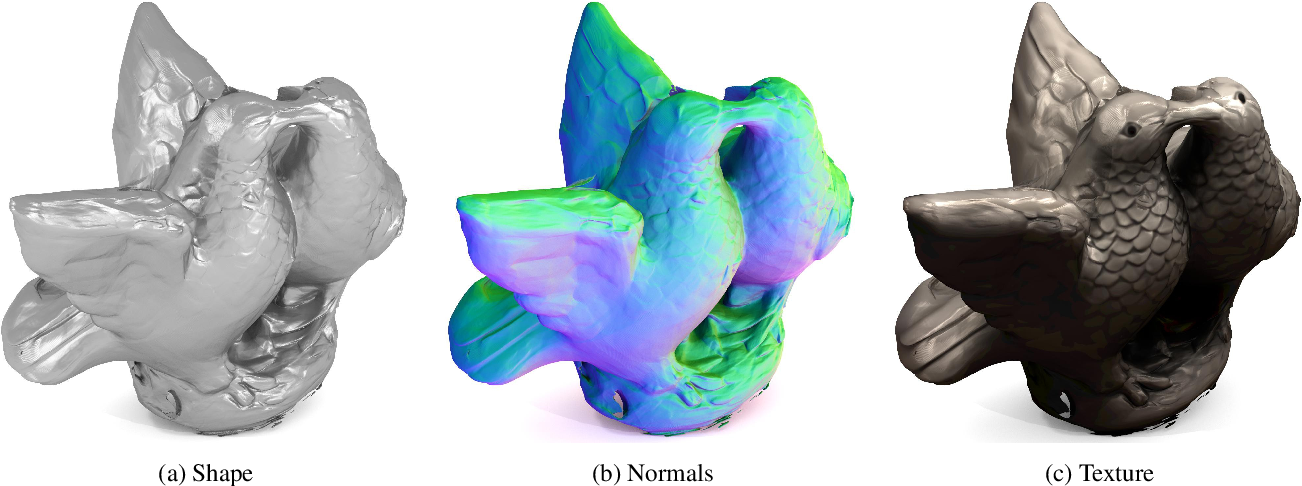
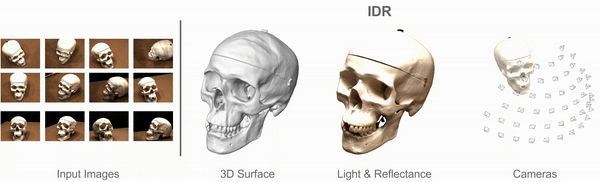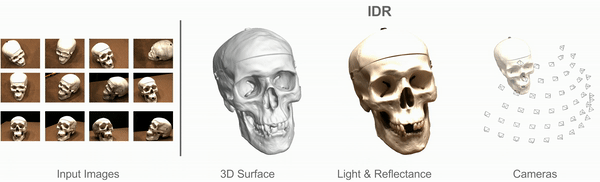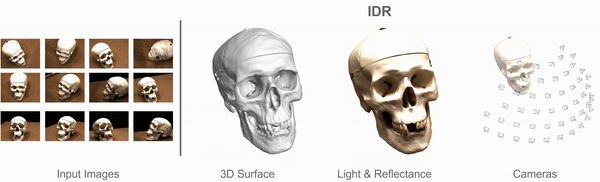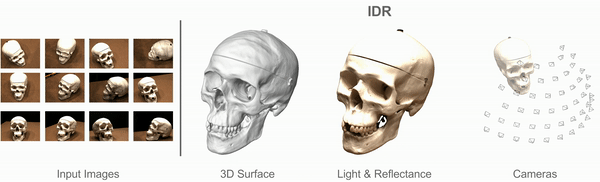
Implicit Differentiable Rendering
Multiview 3D Surface Reconstruction
Input: Collection of 2D images (masked)
with rough or noisy camera info.
Targets:
- Geometry
- Appearance (BRDF, lighting conditions)
- Cameras
Method:
Geometry:
\mathcal{S}_\theta = \{ x\in \mathbb{R}^3 | f(x;\theta) = 0 \}
signed distance function (SDF) +
implicit geometric regularization (IGR)
\theta
- geometry parameters
IDR - Forward pass
R_p(\tau) = \{ c_p + t v_p | t \geq 0 \}
\hat{x}_p = \hat{x}_p(\theta, \tau) = R_p(\tau) \cap \mathcal{S}_\theta
\tau \text{ - camera parameters}
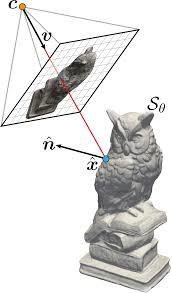
Ray cast:
(first intersection)
p \text{ - pixel}
IDR - Forward pass
L_p(\theta, \gamma, \tau) = M(\hat{x}_p, \hat{n}_p, \hat{z}_p, v_p; \gamma)
\gamma
- appearance parameters
Output (Light Field):
Surface normal
\hat{n}_p(\theta)
Global gometry feature vector
\hat{z}_p(\hat{x}_p; \theta)
Differentiable intersections
\theta_0, \tau_0 - \text{current parameters}
\hat{x}(\theta, \tau) = c + t_0 v - \frac{v}{\nabla_x f(x_0; \theta_0) \cdot v_0} f(c + t_0 v; \theta)
Lemma:
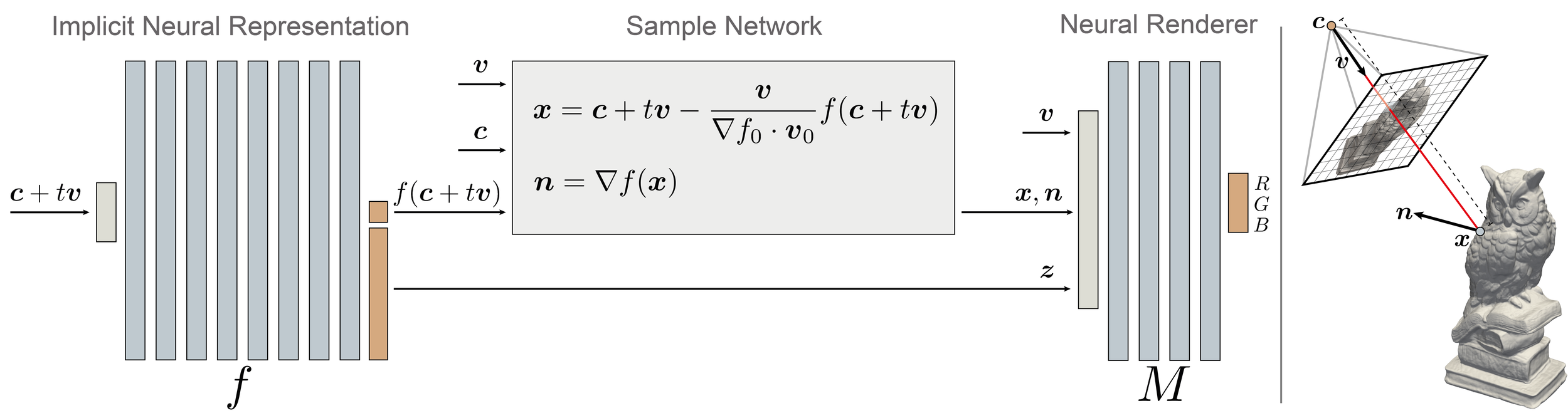
Light Field Approx.
L(\hat{x}, w^o) = L^e(\hat{x}, w^o) + \int\limits_\Omega B(\hat{x}, \hat{n}, w^i, w^o) L^i (\hat{x}, w^i) (\hat{n}\cdot w^i) d w^i
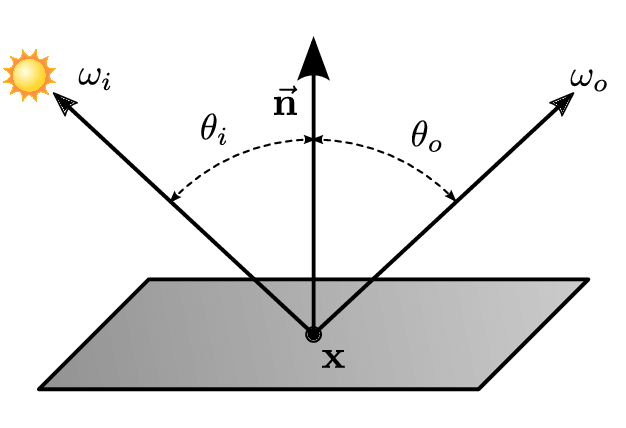
BRDF function
out direction
income direction
emitted
radiance
incoming radiance
= M_0(\hat{x}, \hat{n}, v)
L(\theta, \gamma, \tau) = M(\hat{x}, \hat{n}, v; \gamma)
Results:
Copy of Deep Implicits
By Daniel Yukimura
