Tipos de datos primitivos
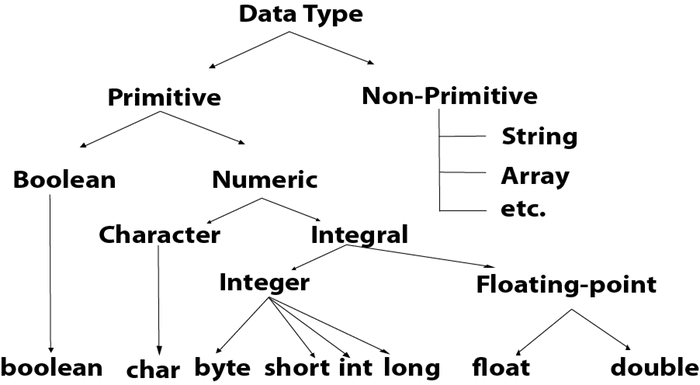
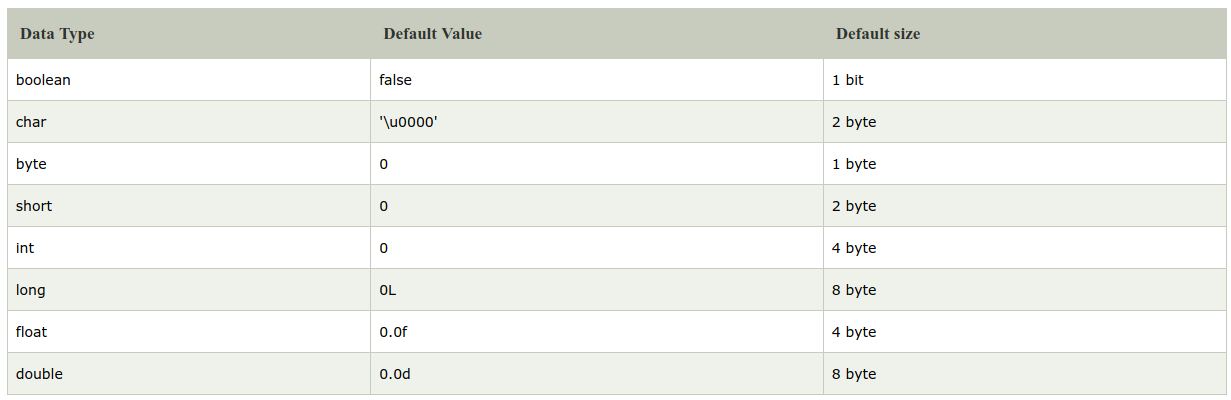
Bytes
A byte is a group of 8 bits. A bit is the most basic unit and can be either 1 or 0. A byte is not just 8 values between 0 and 1, but 256 (28) different combinations (rather permutations) ranging from 00000000 via e.g. 01010101 to 11111111. Thus, one byte can represent a decimal number between 0(00) and 255.
Estructuras de control selectivo
IF
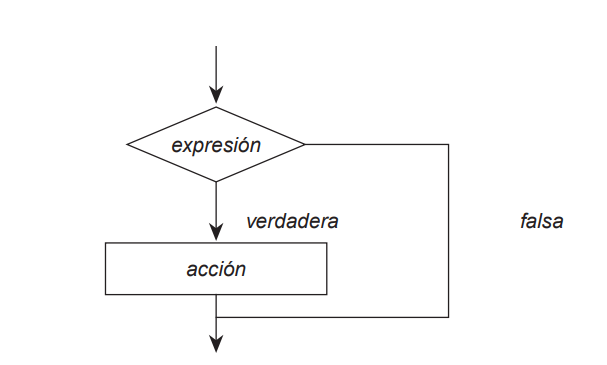

If - else

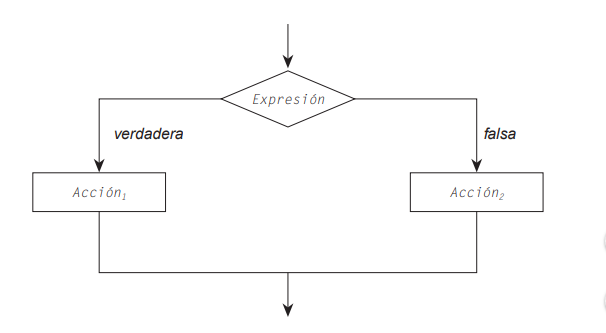
If - else anidado

Ejercicio

Switch

Ejercicio

Operador ternario


Short-circuit
&&, ||
Estructuras de control repetitivo
While
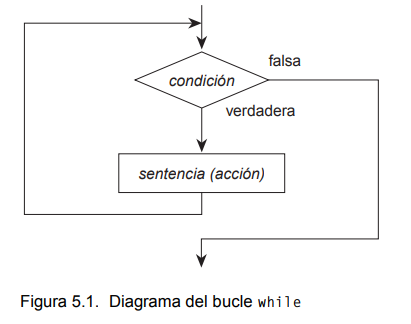
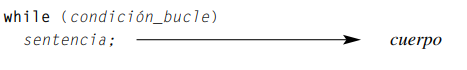
Ejercicio

For

Ejercicio

do ... while
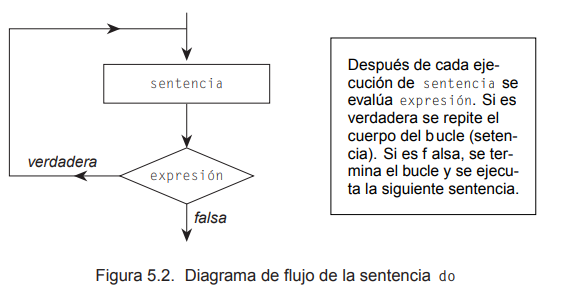

Ejercicio

Evaluación de algoritmos
Orden de magnitud - Big O Notation
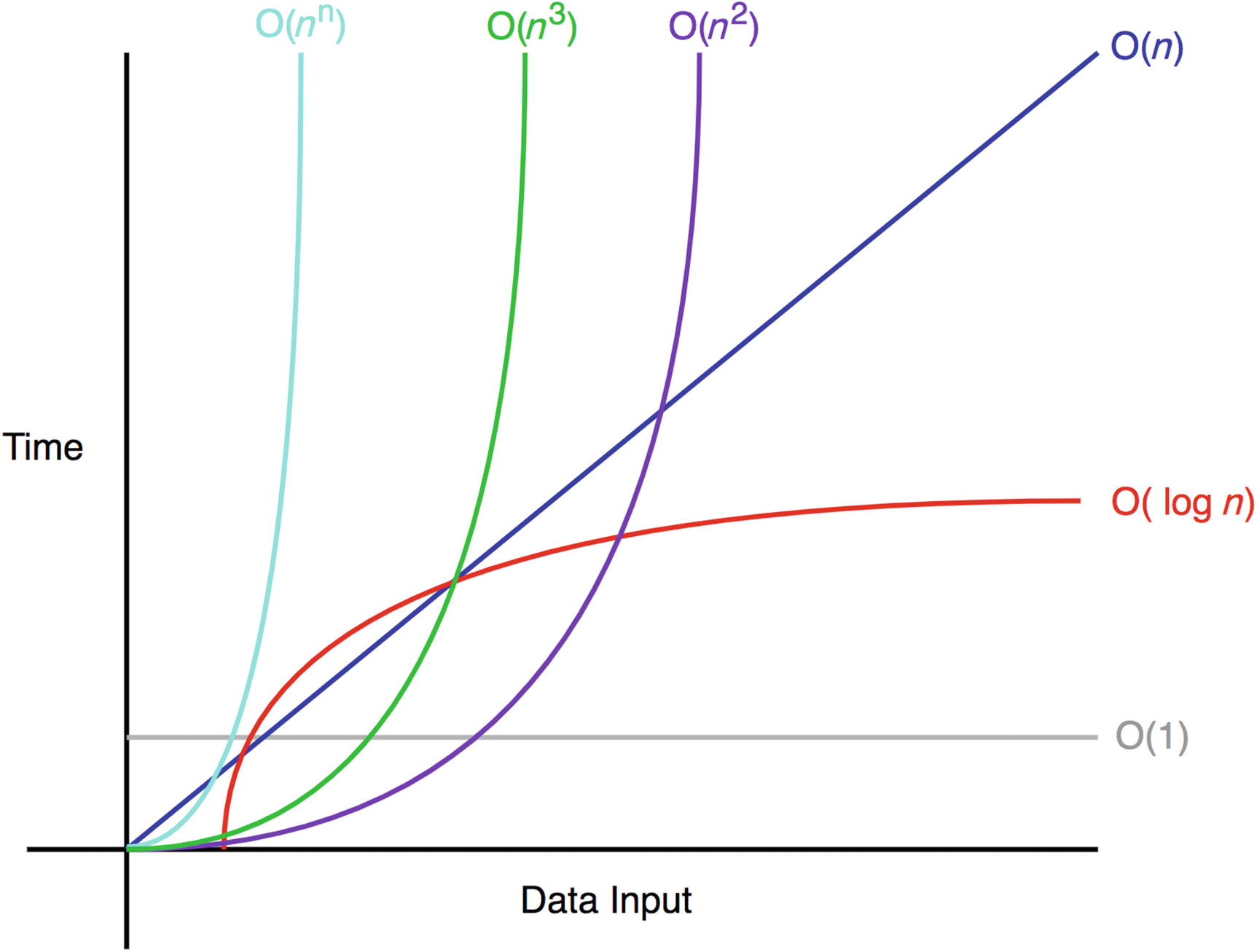
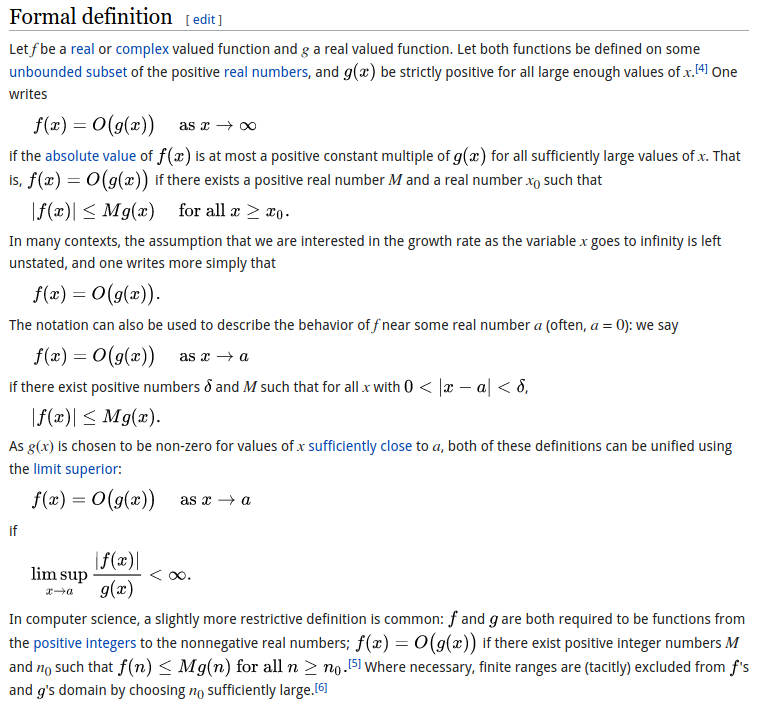
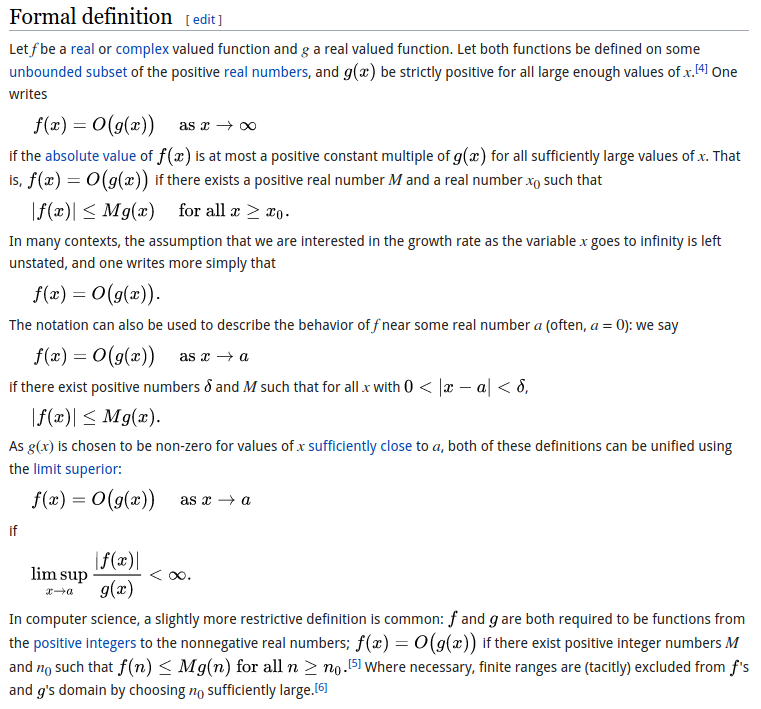
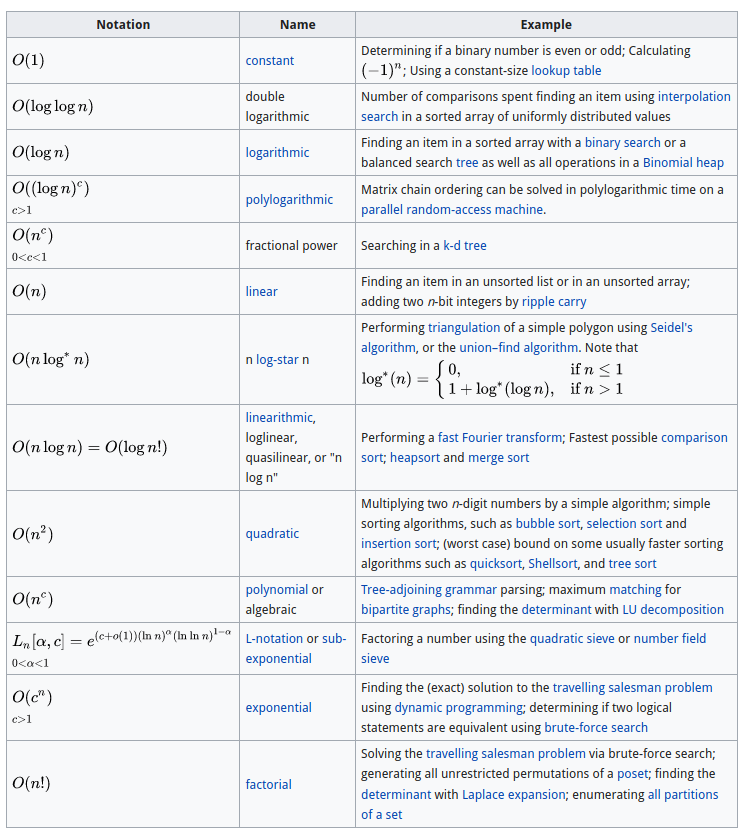


Estructuras de Datos simples
// Online C compiler to run C program online
#include <stdio.h>
#include <math.h>
// Llenar arreglo de valores 1 - 10
// Imprimir la potencia cubica de c/valor
int main() {
int valores[10];
int i = 2;
for (i = 0; i<10; i++) {
valores[i] = i + 1;
//printf("%d \n", valores[i]);
}
for(i = 0; i<10; i++) {
int p = (int) pow(valores[i], 3);
printf("%d^3 = %d \n", valores[i], p);
}
return 0;
}Arrays
Matrices
#include <stdio.h>
#include <math.h>
// En una matriz de 10x10, primera columna es el numero del al 10, y las 9 columnas siguientes es el numero a la potencia de la columna.
// Matriz[2,1] = 2
// Matriz[2,2] = 2 ^ 2 = 4
// Matriz[2,3] = 2 ^ 3 ... 2 ^ 10
int main() {
long valores[10][10];
for (int i = 0; i<10; i++) {
for (int j = 0; j<10; j++) {
valores[i][j] = (long) pow(i+1, j+1);
}
}
for (int i = 0; i<10; i++) {
for (int j = 0; j<10; j++) {
printf("Matriz[%d,%d] = %d^%d = %li \n", i+1, j+1, i+1, j+1, valores[i][j]);
}
}
return 0;
}Strings
#include <stdio.h>
#include <math.h>
int main() {
char alfa[14] = "Hola mundo! :)";
char *alfadir = &alfa;
// HEAP - Espacio dinamico de memoria
//MEM16 ["H"]["o"]["l"]["a"]...[")"]
//MEM17 MEM16
// ROM - Espacio estatico de memoria
// MEM50 MEM16 set ["H"]["o"]["l"]["a"]...[")"]
// MEM51 MEM17 set MEM16
for(int i=0; i<sizeof(alfa); i++) {
printf("%c", alfa[i]);
}
printf("\n%s", alfadir);
return 0;
}Recursividad
// Funciones
// f(x) => y
// sin(x) => a
// sininv(x) => b
// Logica propsicional -> Absurdo
// si sininv(x) es a y sin(x) es a si y solo si sininv(x) = sin(x) => Es un absurdo y es negativo/falso. sininv(x) =/= sin(x)
// [a] => [x]
// [b] => [y]
// fn(type_1) => type_2 ====> type[char/int/double/float/long/Structures/arrays[uni-multi]]
// ascii(int) => char // Convertir un entero en caracter.
// Crear una funcion que retorne la serie de fibonacci hasta un numero n.
// 1 1 2 3 5 7
// a0 = 1 -> inicial
// a1 = a0 + 0 = 1 -> inicial
// a2 = a0 + a1 = 2
// a3 = a1 + a2 = 3
// a4 = a2 + a3 = 3
// a5 = a3 + a4 = 3
// ...
// an = a[n-2] + a[n-1]
int *fibonacci (int n) {
static int fibo[10];
fibo[0] = 1;
fibo[1] = 1;
for (int i = 2; i < n; i++) {
fibo[i] = fibo[i-2] + fibo[i-1];
}
return fibo;
}
/** Prueba de escritorio
* fibonacci(2) => 1 1
* fibo[2]
* fibo [0] = 1
* fibo[1] = 1
* i = 2; 2 < 2? FALSE
* return 1 1
*
* fibonacci(5) => 1 1 2 3 5
* fibo[5] // [0,0,0,0,0]
* fibo[0] = 1
* fibo[1] = 1
* i = 2; 2 < 5? TRUE
* fibo[2] = fibo[2-2] + fibo[2-1] = fibo[0] + fibo[1] = 1 + 1 = 2 // fibo = [1,1,2]
* i = i++ = 2 + 1 = 3
* i = 3; 3 < 5? TRUE
* fibo[3] = fibo[3-2] + fibo[3-1] = fibo[1] + fibo[2] = 1 + 2 = 3 // fibo = [1,1,2,3]
* i = 3 + 1 = 4
* i = 4; 4 < 5? TRUE
* fibo[4] = fibo[4-2] + fibo[4-1] = fibo[2] + fibo[3] = 2 + 3 = 5 // fibo = [1,1,2,3,5]
* i = 4 + 1 = 5
* i = 5; 5 < 5? FALSE
* return [1,1,2,3,5]
*/
int main() {
// Write C code here
int n = 10;
int *fibo = fibonacci(n);
for (int i = 0; i < n; i++) {
printf( "%d\n", *(fibo + i));
}
return 0;
}int r_fibonacci (int n) {
// Parada
// if (sentencia) return valor_por_defecto;
if (n <= 2) return 1;
//if (n == 0) return 1;
// Recursividad
// Codigo normal
return r_fibonacci(n-2) + r_fibonacci(n-1);
}
// MEMORIA
// r_fibonacci(-1)
// r_fibonacci(1-2) + r_fibonacci(1-1)
// r_fibonacci(2-1) // 1
// 1 + r_fibonacci(2-1)
// r_fibonacci(0) + r_fibonacci(1)
// MEMORIA
// 1
// r_fibonacci(1-1) //
// 0 + r_fibonacci(1-1)
// r_fibonacci(2-1) // 1
// 1 + r_fibonacci(2-1)
// r_fibonacci(0) + r_fibonacci(1)
// MEMORIA
// 5
// r_fibonacci (2) // n = 2
// n == 0? 2 == 0? FALSE
// r_fibonacci(2-2) + r_fibonacci(2-1)
// 1 + r_fibonacci(1-1)
// r_fibonacci(2-2) // n = 0
// n == 0? 0 == 0
// return 1
// r_fibonacci(1) // n = 1
// n == 0? 1 == 0? false
// r_fibonacci(1-2) + r_fibonacci(1-1)
// CICLO INFINITO // sin 2da parada
// r_fibonacci(1-2) // r_fibonacci(-1) // n = -1
// n == 0? -1 == 0? false
// r_fibonacci(-1-2) + r_fibonacci(-1-1)
// r_fibonacci(-3) + r_fibonacci(-2)
// r_fibonacci(1-2) // n = -1
// return;Recursividad
def fibonacci(n):
fibo = [1, 1]
for i in range(2, n):
fibo.append(fibo[i-2] + fibo[i-1])
return fibo
n = 10
fibo = fibonacci(n)
print(fibo)Factorial
def factorial(n):
if n == 0:
return 1
else:
return n * factorial(n-1)
print(factorial(4)) # 4! = 4x3x2x1 = 24Fibonacci
No recursivo
Fibonacci
Recursivo
Algoritmos de Ordenamiento

Bubble sort

Selection sort

Quick Sort


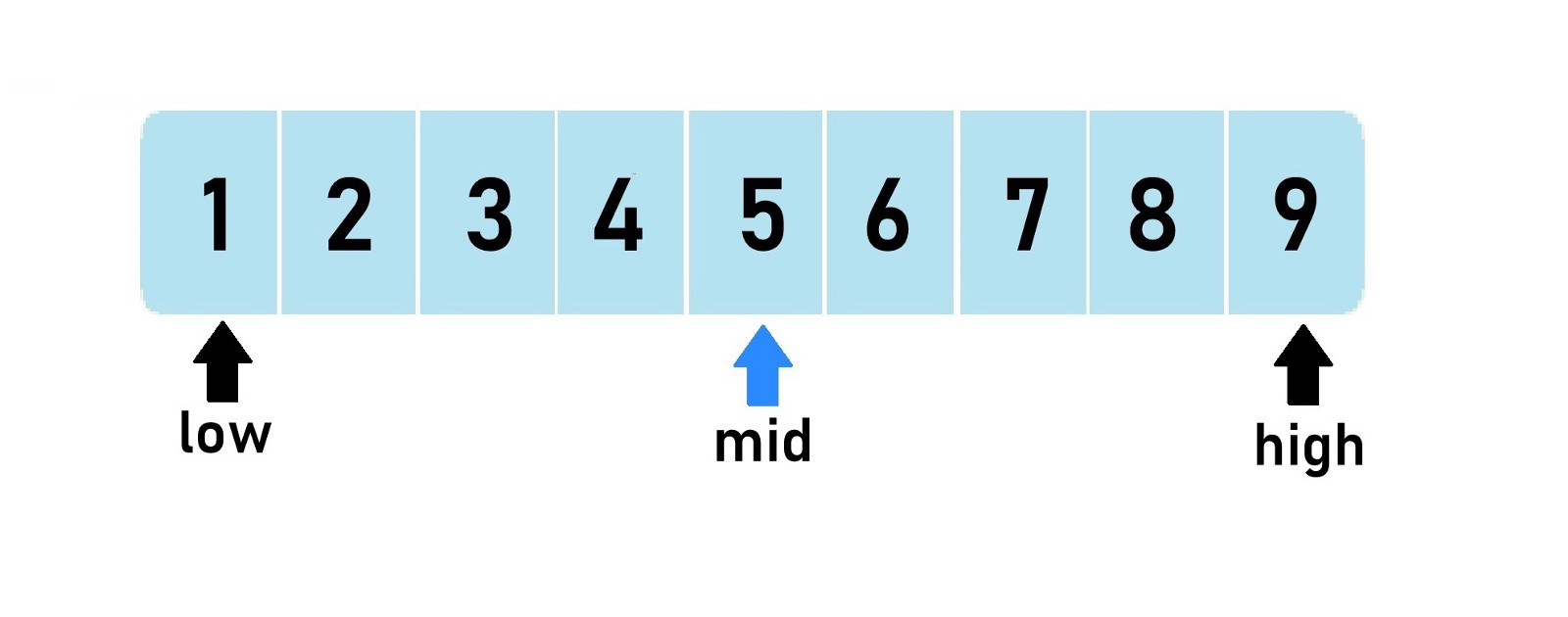
Algoritmos de busqueda
Algoritmos de busqueda

Algoritmos de busqueda
Paradigmas de programacion
LIFO - FIFO
LIFO
Last in first out
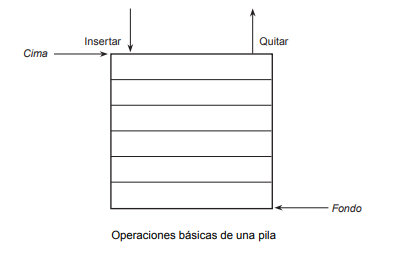
Pila ( Stack )

// Pila.h
class Pila() {
int AnadeP(int dato); // push -> Ponerlo al final
int BorrarP(); // Pop -> Borrar el ultimo -> devolver
bool EsVaciaP(); // empty
Pila Pila() // VaciaP -> Crear la pila vacia
boolean EstallenaP() // Si la pila esta llena
int PrimeroP() // Devuelve el primero
}[1,2,2,3,4,5,X];
pila.push(6);
[1,2,2,3,4,5,6];
[1,2,X,X,X,X,X];
pila.push(6);
[1,2,6,X,X,X,X];
pila.pop(); -> 6
[1,2,X,X,X,X,X];
pila.empty() -> false
pila.isFull() -> falseFIFO
First in First Out
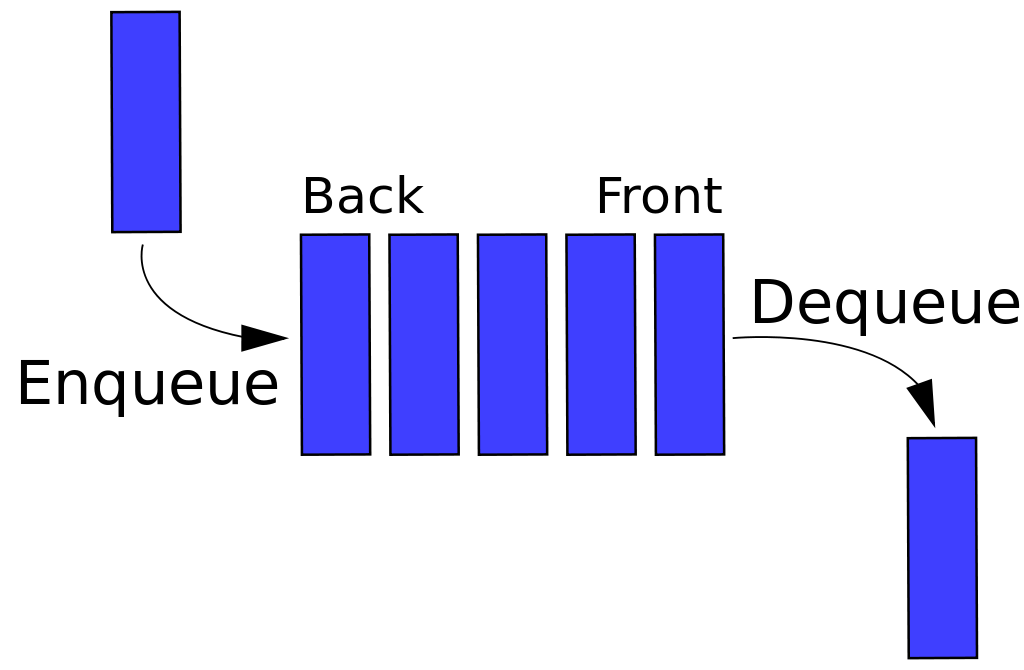
Cola (Queue)

class Cola() {
int AnadeC(int dato); // push -> Ponerlo al final
int BorrarC(); // Pop -> Borra el primero / Mueve todos los valores -1 espacio -> devolver
bool EsVaciaC(); // empty
Cola Cola() // VaciaP -> Crear la cola vacia
boolean EstallenaC() // Si la cola esta llena
int PrimeroC() // Devuelve el primero
}[1,2,2,3,4,5,X];
cola.push(6);
[1,2,2,3,4,5,6];
[1,2,X,X,X,X,X];
cola.push(6);
[1,2,6,X,X,X,X];
cola.pop(); -> 1
[2,6,X,X,X,X,X];
cola.empty() -> false
cola.isFull() -> falseTerminal
C
#include <stdio.h>
int *fibonacci(int n) {
int *fibo = malloc(n * sizeof(int));
fibo[0] = 1;
fibo[1] = 1;
for (int i = 2; i < n; i++) {
fibo[i] = fibo[i-2] + fibo[i-1];
}
return fibo;
}
int main() {
int n = 15;
int *fibo = fibonacci(n);
for (int i = 0; i < n; i++) {
printf("[%d]:%d\n", fibo+i, *(fibo+i));
}
return 0;
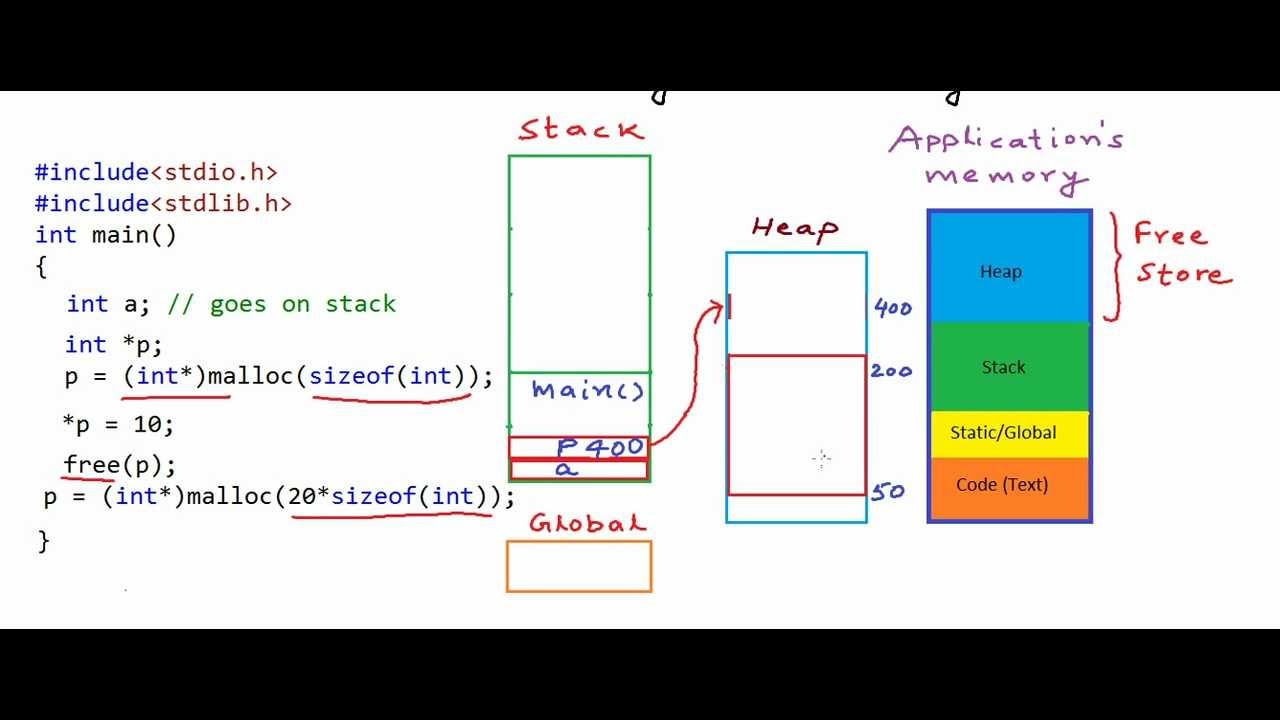
}Malloc
Parametros por Valor / Refencia & Debugging
#include <stdio.h>
// Pure Function
int pure_power(int b) {
return b * b;
}
// Impure Function
int power(int *b) {
*b = 5;
return *b * *b;
}
int main() {
int x = 3;
int pure_p = pure_power(x);
int p = power(&x);
printf("x: %d\n", x);
printf("p: %d\n", p);
printf("pure: %d\n", pure_p);
}
gcc program.c -o program
gdb program
>> break 17
>> run
>> print x
>> print pure_p
>> run
>> quit
deck
By Dave Rivera
deck
- 379



