Toward a Science of Causal Interpretability in Deep Learning for Software Engineering

Pre-Defense

March

2025

David N. Palacio

Department of Computer Science

Φ\Phi
\Phi

Motivating Example:

Code Generation

def countChars(string, character):


count = 0
for letter in string:
    if letter = character:
       count = count + 1
return count

prompt

code completed

pretrained  model

To what extent is the current prevalence of code generation driven by hype?

How reliable is the generated snippet?

def countChars(string, character):


count = 0
for letter in string:
    if letter = character:
       count = count + 1
return count

conditioned

prompt

code completed

pretrained  model

Accuracy ~0.8

Why?

Less Interpretable

How reliable is the generated snippet?

def countChars(string, character):


count = 0
for letter in string:
    if letter = character:
       count = count + 1
return count

conditioned

prompt

code completed

pretrained  model

Accuracy ~0.8

Why?

Less Interpretable

Accuracy is not sufficient

Interpretability is understanding how models make predictions so that decision-makers (e.g., programmers, doctors, judges) can assess the extent to which they can trust models' output

Is the code completed reliably?

First Explanation

def (, ) :

Second  Explanation

Feature Space

CodeFeatures={Spaces,Puntuation}CodeFeatures = \{Spaces, Puntuation\}
CodeFeatures = \{Spaces, Puntuation\}
CodeFeatures={identifiers,variables}CodeFeatures = \{identifiers, variables\}
CodeFeatures = \{identifiers, variables\}
countChars string character

Unreliable Prediction

Trustworthy Prediction

Model understanding is critical in high-stakes domains such as code generation since AI systems can impact the lives of millions of individuals (e.g, health care, criminal justice)

interpretable pretrained model

Facilitating debugging and detecting bias

Providing recourse to practitioners who are negatively affected by predictions

Assessing if and when to trust model predictions when making decisions

Vetting models to determine if they are suitable for deployment in real scenarios

What is Interpretability?

"It is a research field that makes ML systems and their decision-making process understandable to humans" (Doshi-Velez & Kim, 2017)

def countChars(string, character):


count = 0
for letter in string:
    if letter = character:
       count = count + 1
return count

prompt

code completed

pretrained  model

What do the interpretability researchers mean by "understandable to humans"?

 We propose using scientific explanations based on causality to reduce the conceptual understandability gap

Φ\Phi
\Phi
def countChars(string, character):


count = 0
for letter in string:
    if letter = character:
       count = count + 1
return count

prompt

code completed

pretrained  model

To explain a phenomenon is to determine what exactly caused it

Φ\Phi
\Phi

Factors or Treatments

Outcomes

Causal Effect or Explanation

To what extent is the current prevalence of code generation driven by hype?

Pearl's Ladder Of Causation

Pearl introduced a mathematical model of causality based on structural causal models (SCM) and do-calculus, enabling AI systems to distinguish between:

Association

(correlation)

Intervention

(causation)

Counterfactual

Reasoning

Rung 1

Rung 2

Rung 3

Pearl introduced a mathematical model of causality based on structural causal models (SCM) and do-calculus, enabling AI systems to distinguish between:

Association

(correlation)

Intervention

(causation)

Counterfactual

Reasoning

Rung 1

Rung 2

Rung 3

“People who eat ice cream are more likely to swim.”

“If we make people eat ice cream, will they swim more?”

“If people had not eaten ice cream, would they have
gone swimming?”

Components of My Research

1. Preliminaries

deep code generation

2. Associational Interpretability

3. Interventional Interpretability

4. Counterfactual Interpretability

5. Consolidation 

confounding bias

traditional vs. causal interpretability

code rationales

ladder of causation

doCode

autopoitec architectures

future remarks

academic contributions

1. Preliminaries

Generative Software Engineering

p(y∣x)p(y|x)
p(y|x)
def countChars(string, character):
	count = 0
	for letter in string:
    	if letter = character:
        	count = count + 1
	return count

observational data

Statistical Learning Process by Induction: empirical risk minimization or minimizing training error

target function

human-generated data are collected

first approximation

ϵ≈0.4\epsilon \approx 0.4
\epsilon \approx 0.4

learning process is iterative

second approximation

ϵ≈0.01\epsilon \approx 0.01
\epsilon \approx 0.01
p(wt∣dt)p(w_t|d_t)
p(w_t|d_t)

observational data (ie., large general training set)

code generation has been mainly addressed using  self-supervised approaches

Extracted Labels

extract, make

Neural Code Model

Pretrained Model

Self-Supervised Pretraining

Pretext Task

p(wt∣dt)p(w_t|d_t)
p(w_t|d_t)

observational data (ie., large general training set)

code generation has been mainly addressed using  self-supervised approaches

Extracted Labels

extract, make

Neural Code Model

Pretrained Model

Self-Supervised Pretraining

target specific dataset

Labels

Pretrained Model

Final Model

Finetuning on target dataset

Transfer Learning

Pretext Task

Downstream Task

p(wt∣w1...t−1)p(w_t|w_{1...t-1})
p(w_t|w_{1...t-1}) 
def countChars(string, character):
	count = 0
	for letter in string:
    	if letter = character:
        	count = count + 1
	return count

observational data

Autoregressive

def

count

Chars

count =

?

w1w_1
w_1
w2w_2
w_2
w3w_3
w_3
wt−1w_{t-1}
w_{t-1}
wtw_t
w_t

Code generation uses self-prediction (a self-supervised strategy):

autoregressive or masking (i.e., hiding parts of inputs)

p(wt∣w1...t−1)p(w_t|w_{1...t-1})
p(w_t|w_{1...t-1}) 
def countChars(string, character):
	count = 0
	for letter in string:
    	if letter = character:
        	count = count + 1
	return count

observational data

Code generation uses self-prediction (a self-supervised strategy):

autoregressive or masking (i.e., hiding parts of inputs)

Autoregressive

Masking

def count[mask](string, character):
	count = 0
	for letter in string:
    	if letter = character:
        	count = count + 1
	return count

[masked]

def

count

Chars

count =

?

w1w_1
w_1
w2w_2
w_2
w3w_3
w_3
wt−1w_{t-1}
w_{t-1}
wtw_t
w_t

def

count

[mask]

w1w_1
w_1
w2w_2
w_2
wtw_t
w_t

(string

w3w_3
w_3
p(wt∣w1...n)p(w_t|w_{1...n})
p(w_t|w_{1...n})

count

wnw_n
w_n
p(wt∣w1...t−1)p(w_t|w_{1...t-1})
p(w_t|w_{1...t-1})

Neural Architectures

Autoregressive

Masking

p(wt∣w1...n)p(w_t|w_{1...n})
p(w_t|w_{1...n})

NCMs: GPT, RNNs

NCMs: BART, BERT

Some examples of generative software engineering

Automatic Bug Fixing

(Tufano, et al, TOSEM'19)

Learning Code Changes (Tufano, et al, ICSE'19)

Assert Statements Generation (Watson, et al, ICSE'20)

Clone Detection (White, et al, ASE'16)

Learning to Identify Security Requirements (Palacio, et al, ICSME'19)

1. Preliminaries

Confounding Bias in Software Engineering

Counfounding Example:

Disparities in Gender Classification

Aggregated metrics obfuscate key information about where the system tends to success or fail (Burnell et al., 2023)

Neural Classifier

Accuracy of 90%

Segregated metrics enhance the explanation of prediction performance

Neural Classifier

Darker Skin Woman

Lighter Skin Man

Error:

34.7%

Error:

0.8%

Simpson's Paradox: Confounders affect the correlation

Darker Skin Woman

Lighter Skin Man

Error:

34.7%

Error:

0.8%

Accuracy of 90%

Aggregated Metrics

Segregated Metrics

What about software data?

Disparities in Code Generation

p(wt∣dt)p(w_t|d_t)
p(w_t|d_t)
def countChars(string, character):
	count = 0
	for letter in string:
    	if letter = character:
        	count = count + 1
	return count

sampling

unconditioned

def countChars(string, character):


	count = 0
	for letter in string:
    	if letter = character:
        	count = count + 1
	return count

conditioned

prompt

completed

generated

codegen-mono-2b

How can we evaluate (autoregressive) code generation?

def countChars(string, character):
	count = 0
	for letter in string:
    	if letter = character:
        	count = count + 1
	return count

unconditioned

def countChars(string, character):


count = 0
for letter in string:
    if letter = character:
       count = count + 1
return count

conditioned

prompt

completed

pretrained  model

generated snippet

unconditioned sampling

pretrained  model

Code Feaseability

Aggregated Metrics

Accuracy

Perplexity

CodeBLEU

Semantic Distance

sampling

p(wt∣dt)p(w_t|d_t)
p(w_t|d_t)

sampling

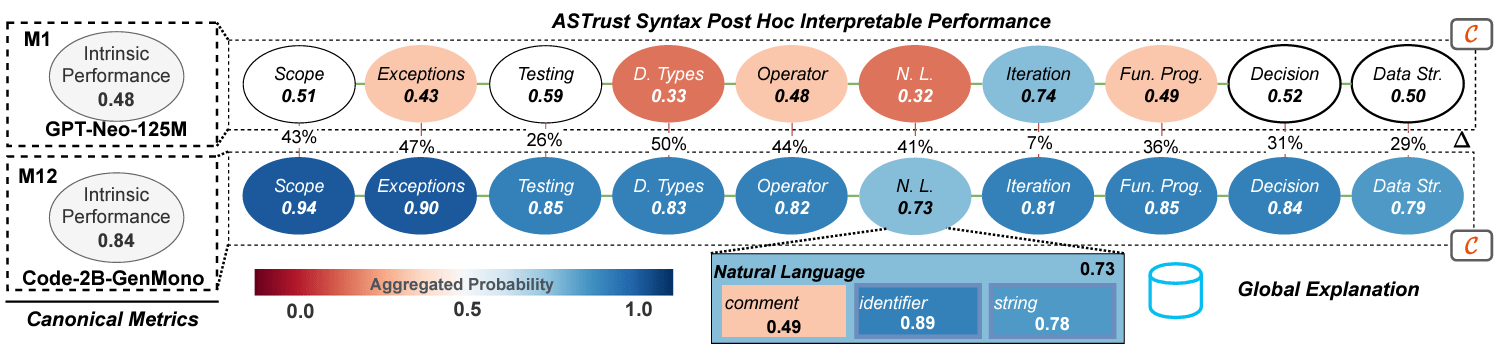
Aggregated Accuracy ~0.84

feasibility area

Segregated Accuracy by Code Features

High dimention accuracy manifold

natural language ~0.72

-  comments (0.49)

-  string (0.78)

-  identifier (0.89)

types ~0.83

 -  float (0.78)

 -  integer (0.87)

decision ~0.84

 -  if_statement (0.78)

 -  elif (0.79)

codegen-mono-2b

natural language ~0.72

-  comments (0.49)

-  string (0.78)

-  identifier (0.89)

types ~0.83

 -  float (0.78)

 -  integer (0.87)

decision ~0.84

 -  if_statement (0.78)

 -  elif (0.79)

Darker Skin Woman

Lighter Skin Man

Error:

34.7%

Error:

0.8%

Confounding Variables allow us to decompose the performance into meaningful clusters

gender classification

code generation

z={skin−types}z = \{skin-types\}
z = \{skin-types\}
z={syntax−concepts}z = \{syntax-concepts\}
z = \{syntax-concepts\}

Observation: Manifold Partition

Aggregated measures offer a partial understanding of neural models' inference process, while partitions make the measures more interpretable. 

How do we know how partitioning or which partitions are correct?

Syntax (De)Composition

Segregated Accuracy by Code Features

natural language ~0.72

-  comments (0.49)

-  string (0.78)

-  identifier (0.89)

types ~0.83

 -  float (0.78)

 -  integer (0.87)

decision ~0.84

 -  if_statement (0.78)

 -  elif (0.79)

Aggregated Accuracy ~0.84

feasibility area

High dimention manifold

Syntax (De)Composition: A manifold partition of the intrinsic metric space (e.g., accuracy space)

Statistical Control

Syntax (De)Composition is based on two mathematical formalisms: alignment and clustering

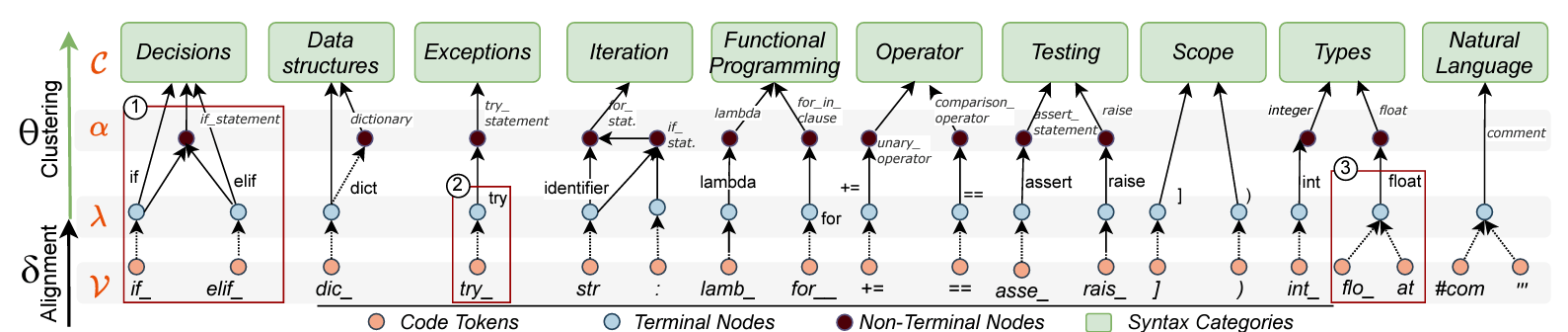
Syntax (De)composition allows the partitioning of manifold space into syntax-based concepts

Scope Concepts are related to termination keywords of the language: '{', '}', 'return'

Disparities in Code Generation

Acceptable Prediction

Confounding Bias is purely a Causal Inference Concept (not a statistical one)

This work goes beyond correlational analysis by proposing interpretability methods to control for confounders

1. Preliminaries

Causal vs. Traditional Interpretability

How do we attain model interpretability?

The taxonomy of traditional interpretability methods

Interpretablity

Intrinsic:

Self-explaining AI

Bottom-Up:

Mechanistic

Top-Down:

Concept-Based

Post-Hoc

How do we attain model interpretability?

The taxonomy of traditional interpretability methods

Interpretablity

Intrinsic:

Self-explaining AI

Bottom-Up:

Mechanistic

Top-Down:

Concept-Based

Post-Hoc

complex model

p(wt∣w1...t−1)p(w_t|w_{1...t-1})
p(w_t|w_{1...t-1})

autoregressive

extract interpretability features

prompts/inputs

outputs

inner parts (e.g, layers, neurons)

Interpreter or Explainer

Simpler Models or Explanations

Interpretability Pipeline

What is an explanation?

An explanation describes the model behavior and should be faithful and understandable.

Explanation

Complex Model

Practitioners

faithful (or aligned)

understandable

Model Parameters (e.g, coefficients, weights, attention layers)

Examples of predictions (e.g., generated code, snippet, bug fix)

Most important features or data points

Counterfactual Explanations / Causal Explanations

An explanation can have different scopes: local and global

Explanation

Global

Local

Explain overall behavior

Help to detect biases at a high level

Help vet if the model is suitable for deployment

Explain specific domain samples

Help to detect biases in the local neighborhood

Help vet if individual samples are being generated for the right reasons

Instance

def countChars(string, character):
	count = 0
	for letter in string:
    	if letter = character:
        	count = count + 1
	return count

sample

One data-point

What is causality?

David Hume [1775]: We are limited to observations. The only thing we experience is that some events are conjoined. 

Aristotle [322 a.C]: Why-type questions is the essence of scientific explanations.

[1747 James Lind - Early 20th century Neyman and Fisher]

The idea of Interventions:

Babies and Experimentation

Conditioning Learning

Association

The holy grail of the scientific method: Randomized Controlled Trials (RCT)

Judea Pearl [21st Century]: A causal link exists in two variables if a change in A can also be detected in B.  

Experiments are not always available. To draw a causal conclusion, data itself is insufficient; we also need a Causal Model. 

Bunge & Cartwright [Later 20th Century]

  • Both reject Humean causation (which sees causality as just a regular sequence of events);

  • Both emphasize mechanisms over statistical correlations in determining causal relationships.

Intuitively, the Causal Effect is a measure or magnitude of the influence of a variable T on another variable Y . In Causal Interpretability for SE, we are interested in understanding how code predictions would react under different input data (or hyperparameter tuning).

TT
T

Treatment:

Bugs in Code

Y=p(wt∣w<t)Y = p(w_{t}|w_{< t})
Y = p(w_{t}|w_{< t})

Potential Outcome:

Code Prediction

?

τi=YiFixed−YiBuggy\tau_{i} = Y_{i}^{Fixed} - Y_{i}^{Buggy}
\tau_{i} = Y_{i}^{Fixed} - Y_{i}^{Buggy}

treatments

potential outcomes

confounders

causal effect

τi=YiFixed−YiBuggy\tau_{i} = Y_{i}^{Fixed} - Y_{i}^{Buggy}
\tau_{i} = Y_{i}^{Fixed} - Y_{i}^{Buggy}

treatment effect of a snippet i

outcome for snippet i when they recived treatment [T=Fixed]

outcome for the same snippet i when they did not recived treatment [T=Buggy]

Causality: "T causes Y if Y listens to T". That is, if we change T, we also have to observe a change in Y (Pearl, 2019)

How can we formulate causal questions?

The Pearl's Ladder of Causation

Q1=P(Y∣T)Q_1 = P(Y|T)
Q_1 = P(Y|T)
Q2=P(Y∣do{T})Q_2 = P(Y|do\{T\})
Q_2 = P(Y|do\{T\})
Q3=P(yt∣t′,y′)Q_3 = P(y_t|t',y')
Q_3 = P(y_t|t',y')

Level 3: Counterfactual (imagining)

Level 2:

Intervention (doing)

Level 1:

Association (observing)

How is the code prediction Y related to (testing) code data with bugs T ?

To what extend does a (test) buggy sequence impact error learning or code prediction?

Would the model generate accurate code predictions if bugs had been removed from training code data? 

Pearl introduces different levels of interpretability and argues that generating counterfactual explanations is the way to achieve the highest level of interpretability.

Causal Interpretability occurs at different levels

Q1=P(Y∣T)Q_1 = P(Y|T)
Q_1 = P(Y|T)
Q2=P(Y∣do{T})Q_2 = P(Y|do\{T\})
Q_2 = P(Y|do\{T\})
Q3=P(yt∣t′,y′)Q_3 = P(y_t|t',y')
Q_3 = P(y_t|t',y')

Level 3: Counterfactual

Level 2:

Intervention

Level 1:

Association

Associational Interpretability

(Traditional Interpretability is at this level)

Interventional Interpretability

Conterfactual Interpretability

All these queries can be approximated using a Structural Causal Model

We encode causal relationships between variables in a Structural Causal Model. This graph is composed of endogenous (or observable) variables (e.g., Treatments, Potential Outcomes, Confounders) and exogenous (or noise) variables

Graph

TT
T
YY
Y
ZZ
Z
UtU_t
U_t
UyU_y
U_y
UzU_z
U_z

We encode causal relationships between variables in a Structural Causal Model. This graph is composed of endogenous (or observable) variables (e.g., Treatments, Potential Outcomes, Confounders) and exogenous (or noise) variables

Both representations (graph and equations) refer to the same object: a data-generating process

Graph

TT
T
YY
Y
ZZ
Z

Functional Relationships

UtU_t
U_t
UyU_y
U_y
UzU_z
U_z
Z:=fZ(Uz)Z := f_Z(U_z)
Z := f_Z(U_z)
T:=fT(Z,Ut)T := f_T(Z,U_t)
T := f_T(Z,U_t)
Y:=fY(Z,T,Uy)Y := f_Y(Z,T,U_y)
Y := f_Y(Z,T,U_y)

:= is a walrus operator (directional or asymmetric relations)

Causal Interpretability is a mathematical and causal inference framework by which Neural Code Models are interpreted or explained from a causal assumption encoded in a Structural Causal Graph

complex model

p(wt∣w1...t−1)p(w_t|w_{1...t-1})
p(w_t|w_{1...t-1})

autoregressive

extract interpretability features

feasible snippets

output logits

causal interpretability

causal explanations

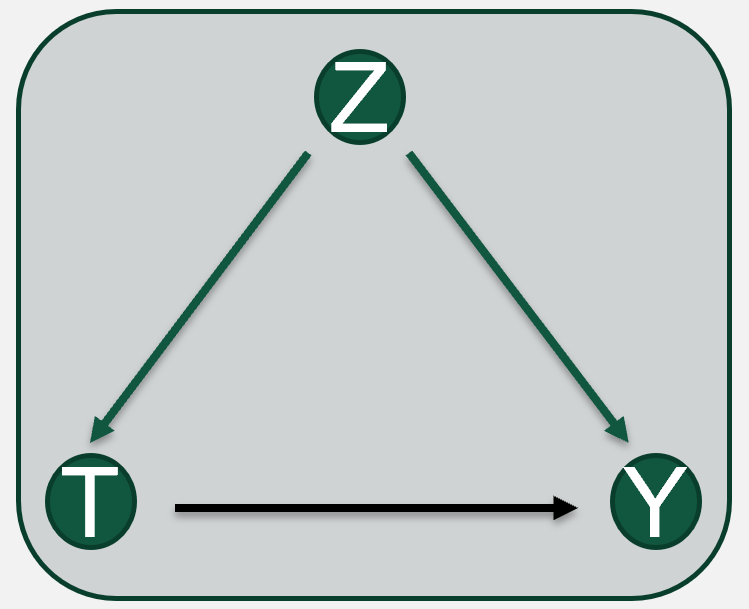
Structural Causal Model (SCM)

Test data with buggy code is negatively affecting code predictions of syntax operators {'+','-'} by 40%

  • [Association] Method 1: TraceXplainer
  • [Association] Method 2: Code Rationales

Rung 1

Rung 2

Rung 3

Three causal methods are proposed to explain code generation at different levels/rungs

Association

(correlation)

Intervention

(causation)

Counterfactual

Reasoning

  • [Intervention] Method 3: doCode
  • [Counterfactual] Method 4: Autopoietic Architectures

2. Associational Interpretability

When correlations are useful

  • [Association] Method 1: TraceXplainer
  • [Association] Method 2: Code Rationales

Rung 1

Association

(correlation)

Method 2: Code Rationales

Rationalizing Language Models contributes to understanding code predictions by searching a set of concepts that best interpret the relationships between input and output tokens.

complex model

p(wt∣w1...t−1)p(w_t|w_{1...t-1})
p(w_t|w_{1...t-1})

autoregressive

extract interpretability features

compatible model

prompts

Code Rationales

Set of Rationales (or important F)

method 2

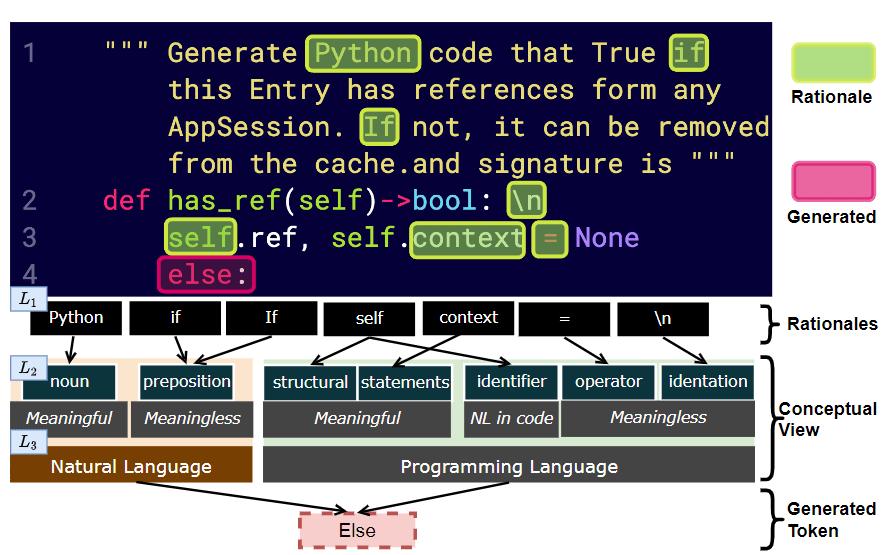
Rationalization is finding a group of tokens that best predict the next token using syntax (de)composition

3. Interventional Interpretability

Fundamental of doCode

  • [Association] Method 1: TraceXplainer
  • [Association] Method 2: Code Rationales

Rung 1

Rung 2

Association

(correlation)

Intervention

(causation)

  • [Intervention] Method 3: doCode

To what extent is the current prevalence of code generation driven by hype?

Pearl's Ladder Of Causation

doCode

Pearl's Ladder Of Causation

Method 3: doCode

Motivating Example: Can an autoregressive model predict a snippet with buggy sequences?

def countChars(string, character):
	count = 0
	for letter in string:
    	if letter = character:
        	count = count + 1
	return count

feasible correct snippet

codegen-mono-2b

count

=

count

+

count

=

+

-

=

+

0.6

0.4

0.01

0.01

0.4

0.6

0.01

0.01

0.5

0.4

0.01

0.01

0.05

0.04

0.01

0.8

p(wt∣w<t−1)p(w_t|w_{< t-1})
p(w_t|w_{< t-1})
p(wt+1∣w<t−2)p(w_{t+1}|w_{< t-2})
p(w_{t+1}|w_{< t-2})
p(wt+2∣w<t−3)p(w_{t+2}|w_{< t-3})
p(w_{t+2}|w_{< t-3})
p(wt+3∣w<t−4)p(w_{t+3}|w_{< t-4})
p(w_{t+3}|w_{< t-4})

def

p(w1∣w0)p(w_1|w_{0})
p(w_1|w_{0})
T1T_1
T_1

...

Motivating Example: Can an autoregressive model predict a snippet with buggy sequences?

def countChars(string, character):
	count = 0
	for letter in string:
    	if letter = character:
        	count = count + 1
	return count

feasible correct snippet

codegen-mono-2b

def countChars(string, character):
	count = 0
	for letter in string:
    	if letter = character:
        	count = count - 1
	return count

feasible buggy snippet (line 5)

count

=

count

+

count

=

+

-

=

+

count

=

count

-

count

=

+

-

=

+

-

0.6

0.4

0.01

0.01

0.6

0.4

0.01

0.01

0.4

0.6

0.01

0.01

0.4

0.6

0.01

0.01

0.5

0.4

0.01

0.01

0.5

0.4

0.01

0.01

0.05

0.04

0.01

0.8

0.05

0.04

0.01

0.8

p(wt∣w<t−1)p(w_t|w_{< t-1})
p(w_t|w_{< t-1})
p(wt+1∣w<t−2)p(w_{t+1}|w_{< t-2})
p(w_{t+1}|w_{< t-2})
p(wt+2∣w<t−3)p(w_{t+2}|w_{< t-3})
p(w_{t+2}|w_{< t-3})
p(wt+3∣w<t−4)p(w_{t+3}|w_{< t-4})
p(w_{t+3}|w_{< t-4})

def

def

p(w1∣w0)p(w_1|w_{0})
p(w_1|w_{0})
T1T_1
T_1
T0T_0
T_0

...

...

To what extend does a buggy sequence impact error learning or code prediction?

def countChars(string, character):
	count = 0
	for letter in string:
    	if letter = character:
        	count = count + 1
	return count

feasible correct snippet

codegen-mono-2b

def countChars(string, character):
	count = 0
	for letter in string:
    	if letter = character:
        	count = count - 1
	return count

feasible buggy snippet (line 5)

=

count

+

-

0.4

0.6

0.01

0.01

0.5

0.4

0.01

0.01

0.05

0.04

0.01

0.8

0.05

0.04

0.01

0.8

p(wt+1∣w<t−2)p(w_{t+1}|w_{< t-2})
p(w_{t+1}|w_{< t-2})
p(wt+2∣w<t−3)p(w_{t+2}|w_{< t-3})
p(w_{t+2}|w_{< t-3})
p(wt+3∣w<t−4)p(w_{t+3}|w_{< t-4})
p(w_{t+3}|w_{< t-4})

correct snippet

buggy snippet

count

=

+

-

=

+

-

T1T_1
T_1
T0T_0
T_0

context

def

...

To what extend does a buggy sequence impact error learning or code prediction?

def countChars(string, character):
	count = 0
	for letter in string:
    	if letter = character:
        	count = count + 1
	return count

feasible correct snippet

codegen-mono-2b

def countChars(string, character):
	count = 0
	for letter in string:
    	if letter = character:
        	count = count - 1
	return count

feasible buggy snippet (line 5)

=

count

+

-

0.4

0.6

0.01

0.01

0.5

0.4

0.01

0.01

0.05

0.04

0.01

0.8

0.05

0.04

0.01

0.8

p(wt+1∣w<t−2)p(w_{t+1}|w_{< t-2})
p(w_{t+1}|w_{< t-2})
p(wt+2∣w<t−3)p(w_{t+2}|w_{< t-3})
p(w_{t+2}|w_{< t-3})
p(wt+3∣w<t−4)p(w_{t+3}|w_{< t-4})
p(w_{t+3}|w_{< t-4})

correct snippet

buggy snippet

count

=

+

-

=

+

-

T1T_1
T_1
T0T_0
T_0
TT
T

Treatment:

Bugs in Code

Y=p(wt∣w<t)Y = p(w_{t}|w_{< t})
Y = p(w_{t}|w_{< t})

Potential Outcome:

Code Prediction

average causal effect ?

context

def

...

Assume a given correlation between T and Y, then we can draft a Causal Explanation for Code Generation

TT
T

Treatment:

Bugs in Code

Y=p(wt∣w<t)Y = p(w_{t}|w_{< t})
Y = p(w_{t}|w_{< t})

Potential Outcome:

Code Prediction

Corr = -0.8

Test data with buggy code is negatively affecting code predictions of syntax operators {'+','-'} by 80%

Causal Explanation:

What if the relationship between the treatment and the outcome is spurious?

The relationship between T and Y can be confounded by a third variable Z, we need a technique to control for the confounding effect

TT
T

Treatment:

Bugs in Code

Y=p(wt∣w<t)Y = p(w_{t}|w_{< t})
Y = p(w_{t}|w_{< t})

Potential Outcome:

Code Prediction

Test data with buggy code is negatively affecting code predictions of syntax operators {'+','-'} by___ ?

Causal Explanation:

ZZ
Z

Confounder:

Sequence Size

causal effect = ?

Causal Inference helps us to control for confounding bias using graphical methods

Test data with buggy code is negatively affecting code predictions of syntax operators {'+','-'} by 40%

Causal Explanation:

TT
T

Treatment:

Bugs in Code

Y=p(wt∣w<t)Y = p(w_{t}|w_{< t})
Y = p(w_{t}|w_{< t})

Potential Outcome:

Code Prediction

ZZ
Z

Confounder:

Sequence Size

causal effect = -0.4

A mathematical language is required to formulate causal queries for code generation

TT
T

Treatment:

Bugs in Code

Y=p(wt∣w<t)Y = p(w_{t}|w_{< t})
Y = p(w_{t}|w_{< t})

Potential Outcome:

Code Prediction

Q=P(Y∣do(T))Q = P(Y|do(T))
Q = P(Y|do(T))

To what extent does a (test) buggy sequence impact error learning or code prediction?

doCode operates at the intervention level

Q2=P(Y∣do(T))Q_2 = P(Y|do(T))
Q_2 = P(Y|do(T))
docodedo_{code}
do_{code}

complex model

p(wt∣w1...t−1)p(w_t|w_{1...t-1})
p(w_t|w_{1...t-1})

autoregressive

extract interpretability features

feasible snippets

output logits

causal interpretability

causal explanations

method 3

Structural Causal Model (SCM)

Training data with buggy code is negatively affecting code predictions of syntax operators {'+','-'} by 40%

To what extent does a (test) buggy sequence impact error learning or code prediction?

3. Interventional Interpretability

The math of doCode

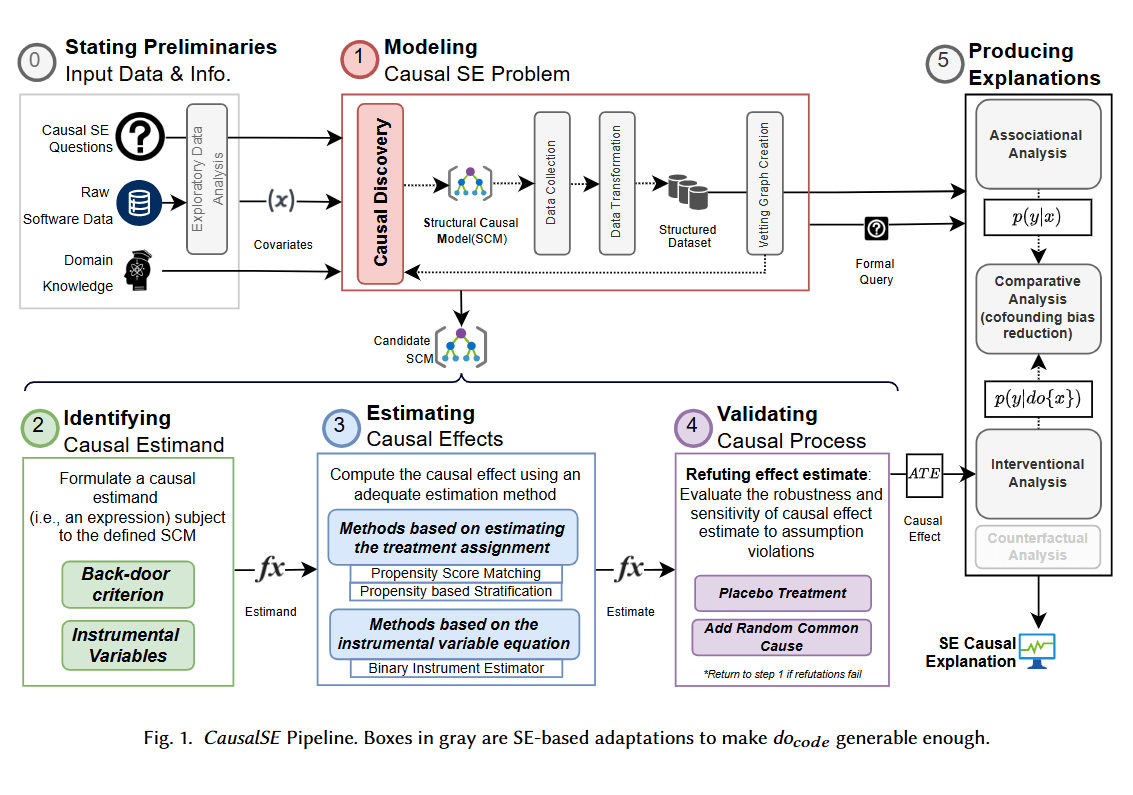
The doCode pipeline is based on Pearl's Causal Theory

1. Modeling

2. Identification

4. Validation

3. Estimation

causal explanations

domain knowledge

input software data

exploratory analysis

Encode causal assumptions in a graph

Formulate a causal estimand

Structural Causal Graph

Math Expression

Compute a Causal Effect using an estimation method

Evaluate the robustness of estimated causal effect

Causal Estimation

Step 1: Modeling Causal Problem

Endogenous nodes can be employed to model relationships among interpretability variables

Structural Causal Model for Interpretability (SCMi)

TT
T
YY
Y
ZZ
Z

treatments

potential outcomes

confounders

Graph Criteria

SE-based (interpretability) interventions

Representation of code predictions

Variables that affects both proposed SE-based interventions and code predictions

BuggyCode

Cross-Entropy Loss

Sequence Size

causal effect

What is a treatment variable?

Treatments are the variables that represent the intervention in the environment. In Causal Interpretability for SE, treatments can represent the subject of the explanation or the "thing" we want to observe and how it affects the code prediction.

TT
T

treatments

potential outcomes

confounders

causal effect

TdataT_{data}
T_{data}

data inteventions

BuggyCode

def countChars(string, character):
	count = 0
	for letter in string:
    	if letter = character:
        	count = count + 1
	return count

feasible correct snippet

def countChars(string, character):
	count = 0
	for letter in string:
    	if letter = character:
        	count = count - 1
	return count

feasible buggy snippet (line 5)

Tdata=1T_{data=1}
T_{data=1}
Tdata=0T_{data=0}
T_{data=0}

Caveat. Treatments can be binary, discrete, or linear variables. We can intervene on data, model parameters, or any other possible SE property. 

TT
T

treatments

potential outcomes

confounders

causal effect

TdataT_{data}
T_{data}

data inteventions

model inteventions

TparamsT_{params}
T_{params}
TpromptT_{prompt}
T_{prompt}
TsyntaxT_{syntax}
T_{syntax}

What is a potential outcome?

Potential Outcomes are the variables that represent the object of the causal effect—the part of the graph that is being affected. In Causal Interpretability for SE, outcomes generally represent the code prediction.

YY
Y

treatments

potential outcomes

confounders

causal effect

YT=BuggyCodeY^{T=BuggyCode}
Y^{T=BuggyCode}
YT=FixedCodeY^{T=FixedCode}
Y^{T=FixedCode}

potential outcome (or cross-entropy loss) under a Treatment T

0.02

0.0002

YFixedCode<YBuggyCodeY^{FixedCode} < Y^{BuggyCode}
Y^{FixedCode} < Y^{BuggyCode}

What are confounders?

Confounders are the variables that represent a common cause between the treatment and the outcome. In Causal Interpretability for SE, confounders are usually code features such as SE metrics, but they can be extended to other variables beyond code.   

ZZ
Z

treatments

potential outcomes

confounders

causal effect

ZZ
Z

SE Metrics as Covariates

McCabe's Complexity

# Varibles

Lines of Code

# Lambda Expressions

# Max nested blocks

# Modifiers

# Returns

# Try-Catch

# Unique Words

Sequence Lenght/Size

Caveat. Not all covariates are confounders

TT
T
YY
Y

Sequence Size as Confounder

TT
T
YY
Y
TT
T
YY
Y

Sequence Size as Mediator

Sequence Size as Instrument

uu
u
ZZ
Z
ZZ
Z
ZZ
Z
uu
u

Back-door

Front-door

Instrumental Variables

Step 2: Identifying Causal Estimand

The causal effect can be represented as a conditional probability (Level 1: Association)

treatments

potential outcomes

confounders

causal effect

τ\tau
\tau
p(Y∣T)p(Y|T)
p(Y|T)

Observational Distribution

BuggyCode Example

τ=p(Y∣T=FixedCode)\tau = p(Y|T = FixedCode)
\tau = p(Y|T = FixedCode)
τ=∑zp(Y∣t,z)p(z∣t)\tau = \sum_zp(Y|t,z)p(z|t)
\tau = \sum_zp(Y|t,z)p(z|t)

The observational distribution does not represent an intervention. We now want to set the variable T to FixedCode using the do-operator  (Level 2: Intevention)

causal effect

τ\tau
\tau
p(Y∣do{T})p(Y|do\{T\})
p(Y|do\{T\})

Interventional Distribution

Adjustment Formula

τ=p(Y∣do{T=FixedCode})\tau = p(Y|do\{T = FixedCode\})
\tau = p(Y|do\{T = FixedCode\})
τ=∑zp(Y∣t,z)p(z)\tau = \sum_zp(Y|t,z)p(z)
\tau = \sum_zp(Y|t,z)p(z)

potential outcomes

confounders

treatments

FixedCode

The back-door criterion is one of the best known techniques to find causal estimands (i.e., adjustment formulas) given a graph. This criterion aims at blocking spurious paths between treatments and outcomes leaving directed paths unaltered (i.e., causal effects). 

causal effect

τ=p(Y∣do{T})\tau = p(Y|do\{T\})
\tau = p(Y|do\{T\})

Interventional Distribution

FixedCode

treatments

potential outcomes

confounders

causal effect

τ=p(Y∣T)\tau = p(Y|T)
\tau = p(Y|T)

Observational Distribution

Variable Z is controled

graph surgery/mutilation

Adjustment Formula or Estimand

p(Y∣do{T})=∑zp(Y∣t,z)p(z)p(Y|do\{T\}) = \sum_zp(Y|t,z)p(z)
p(Y|do\{T\}) = \sum_zp(Y|t,z)p(z)

Interventional Distribution

p(Y∣T)=∑zp(Y∣t,z)p(z∣t)p(Y|T) = \sum_zp(Y|t,z)p(z|t)
p(Y|T) = \sum_zp(Y|t,z)p(z|t)

Observational Distribution

back-door criterion

The back-door, mediation, and front-door criteria are special cases of a more general framework called do-calculus (Pearl, 2009)

Step 3: Estimating Causal Effects

We can use the adjustment formula to compute or estimate causal effects from observational data (Pearl, et al., 2016)

p(y∣do{t})p(y|do\{t\})
p(y|do\{t\})

Interventional Distribution for one data sample

Ei∼p(i)[Y=y∣i,do{T=t}]E_{i\sim p(i)}[Y=y|i,do\{T=t\}]
E_{i\sim p(i)}[Y=y|i,do\{T=t\}]

We can compute for a set of samples (i.e., code snippets) obtaining an ATE (average treatment effect)

Ei∼p(i)[E[Y=y∣i,do{T=1}]−E[Y=y∣i,do{T=0}]]E_{i\sim p(i)}[E[Y=y|i,do\{T=1\}]-E[Y=y|i,do\{T=0\}]]
E_{i\sim p(i)}[E[Y=y|i,do\{T=1\}]-E[Y=y|i,do\{T=0\}]]

For binary treatment (i.e., BuggyCode), we can derive an expected value expression.

Treatment (T=1) means FixedCode

NO Treatment (T=0) means BuggyCode

Note the both expected value terms can be estimated from data using techniques such as propensity score matching, linear regression, or machine learning methods. 

Ei∼p(i)[E[Y=y∣i,do{T=1}]−E[Y=y∣i,do{T=0}]]E_{i\sim p(i)}[E[Y=y|i,do\{T=1\}]-E[Y=y|i,do\{T=0\}]]
E_{i\sim p(i)}[E[Y=y|i,do\{T=1\}]-E[Y=y|i,do\{T=0\}]]

Treatment (T=1) means FixedCode

NO Treatment (T=0) means BuggyCode

def countChars(string, character):
	count = 0
	for letter in string:
    	if letter = character:
        	count = count + 1
	return count

def countChars(string, character):
	count = 0
	for letter in string:
    	if letter = character:
        	count = count - 1
	return count

feasible buggy snippet (line 5)

feasible correct snippet

Correct Snippets Dataset

Buggy Snippets Dataset

Step 4: Validating Causal Process

Assumptions encoded en causal graphs are supported by observations of a data generating process. Testing for the quality of the causal graph fitting the data would be the main issue. This validation comprises two parts: refuting effect estimate and vetting the causal graph. 

Refuting Effect Estimate

Vetting graph creation

treatments

potential outcomes

confounders

τ\tau
\tau
ZZ
Z
YY
Y
ZZ
Z
TT
T
ρ↑\rho \uparrow
\rho \uparrow
ρ↑\rho \uparrow
\rho \uparrow
HH
H

We must assess whether the estimated causal effect (from previous step) is not significantly altered after assumption violations (i.e., refutation methods).  How can we falsify our assumptions?

Add Unobserved Common Cause

treatments

potential outcomes

confounders

τ=p(y∣do(T))\tau = p(y|do(T))
\tau = p(y|do(T))
HH
H

Unobserved Cause

τ=p(y∣do(T),H)\tau = p(y|do(T),H)
\tau = p(y|do(T),H)

should be the same quantity

τ\tau
\tau

Add Random Common Cause

Placebo Treatments

After doCode pipeline, we obtain our validated causal effect quantity!

τ\tau
\tau

1. Modeling

2. Identification

4. Validation

3. Estimation

causal explanations

domain knowledge

input software data

exploratory analysis

Encode causal assumptions in a graph

Formulate a causal estimand

Structural Causal Graph

Math Expression

Compute a Causal Effect using an estimation method

Evaluate the robustness of estimated causal effect

Causal Estimation

τ\tau
\tau

3. Interventional Interpretability

A Case Study in Code Generation

The Causal Interpretability Hypothesis

doCode is a causal interpretability method that aims to make Deep Learning for Software Engineering (DL4SE) systems (e.g., pretrained or LLMs) and their decision-making process understandable for researchers and practitioners

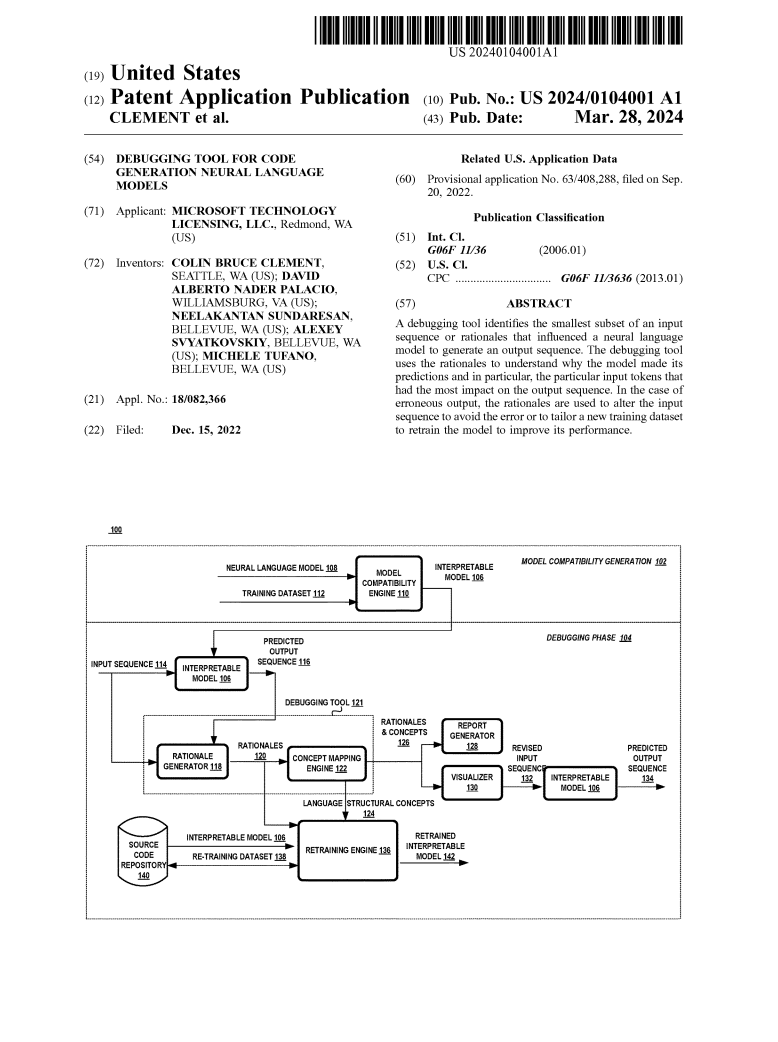
The study proposes four different cases to demonstrate the efficacy and applicability of causal interpretability for code generation

Data-based interventions

Model-based interventions

Syntax Decomposition as Treatments

Prompt Engineering as Treatments

Buggy Code Impact

Inline Comments Impact

Code Clones Impact

# of Layers Impact

# of Units Impact

TdataT_{data}
T_{data}
TparamsT_{params}
T_{params}
TsyntaxT_{syntax}
T_{syntax}
TpromptT_{prompt}
T_{prompt}

On decoder-only models

On encoder-only models

case A

case B

For this talk, I am focusing on two cases:

  • [case A] Data Intervention for BuggyCode
  • [case B] Prompt Intervention 

[case A] Data Intervention for BuggyCode experiment setup. 

Q=P(Y∣do{T})Q = P(Y|do\{T\})
Q = P(Y|do\{T\})
docodedo_{code}
do_{code}
p(wt∣w1...t−1)p(w_t|w_{1...t-1})
p(w_t|w_{1...t-1})

autoregressive

extract interpretability features

feasible snippets

output logits

causal explanations

method 3

Structural Causal Model (SCM)

If we remove bugs from training code data T, will the model generate accurate code predictions Y?

To what extent does a (test) buggy sequence impact error learning or code prediction?

RNNs

GRUs

GPT2

Neural Code Models

Very complex query, we can simplify it

Testbed: BuggyTB 

Training : CodeSearch Net

[case A] Structural Causal Graph proposed (graph hypothesis)

treatments

potential outcomes

confounders

causal effect

Structural Causal Model

Tdata=BuggyCode,FixedCodeT_{data} = BuggyCode, FixedCode
T_{data} = BuggyCode, FixedCode
Y=p(wt∣w<t)Y = p(w_{t}|w_{< t})
Y = p(w_{t}|w_{< t})
Z=SE−MetricsZ = SE-Metrics
Z = SE-Metrics

BuggyTB

Model Outputs

Static Tools

To what extend does a (test) buggy sequence impact error learning or code prediction?

Research Question

[case A] Level 1: Association Results

treatments

potential outcomes

confounders

causal effect

τ=p(Y∣T)\tau = p(Y|T)
\tau = p(Y|T)

Structural Causal Model

To what extend does a (test) buggy sequence impact error learning or code prediction?

Research Question

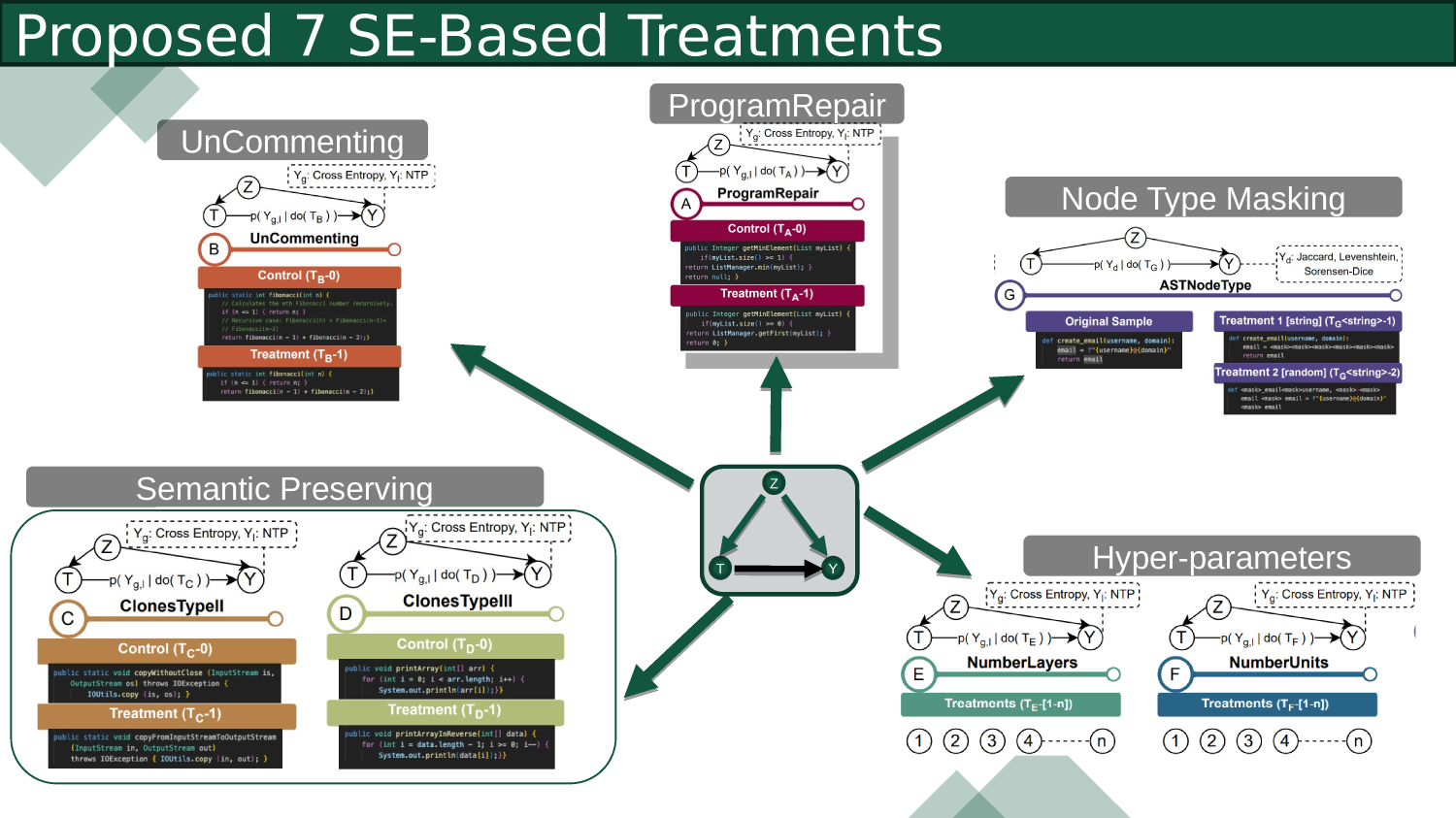
Level 1: Association

RNNs

GRUs

GPT2

0.730

τ\tau
\tau

0.230

0.670

Neural Code Model

[case A] Level 2: Intervention Results

treatments

potential outcomes

confounders

causal effect

Structural Causal Model

To what extend does a (test) buggy sequence impact error learning or code prediction?

Research Question

τ\tau
\tau
τ=p(Y∣T)\tau = p(Y|T)
\tau = p(Y|T)

Level 1: Association

RNNs

GRUs

GPT2

0.730

0.230

0.670

Neural Code Model

Level 2: Intervention

τ=p(Y∣do{T})\tau = p(Y|do\{T\})
\tau = p(Y|do\{T\})

-3.0e-4

-2.3e-5

-2.0e-4

Null Causal Effects after controlling for confounders

[case A] Data Intervention for BuggyCode

Takeaway or Causal Explanation:

 

The presence or absence of buggy code (in the test set) does not appear to causally influence (or explain) the prediction performance of NCMs even under high correlation.

[case B] Prompt Intervention experiment setup. 

Q=P(Y∣do{T})Q = P(Y|do\{T\})
Q = P(Y|do\{T\})
docodedo_{code}
do_{code}
p(wt∣w1...t−1)p(w_t|w_{1...t-1})
p(w_t|w_{1...t-1})

autoregressive

extract interpretability features

code completion

distance metrics

causal explanations

method 3

Structural Causal Model (SCM)

To what extent the type of prompt engineering is influencing the code completion performance?

ChatGPT

Neural Code Models

Testbed: GALERAS

[case B] Structural Causal Graph proposed (graph hypothesis)

treatments

potential outcomes

confounders

causal effect

Structural Causal Model

Tprompt=Control,T1,T2T_{prompt} = Control, T_1, T_2
T_{prompt} = Control, T_1, T_2
Y=LevenshteinY = Levenshtein
Y = Levenshtein
Z=SE−MetricsZ = SE-Metrics
Z = SE-Metrics

GALERAS

Distance Metric

Static Tools

Research Question

To what extent the type of prompt engineering is influencing the code completion performance?

# Complete the following python method: ```{code}``` 
# Write a Python method that starts with ```{code}``` , I need to complete this function. Remove comments, summary and descriptions.
# Remember you have a Python function named {signature}, the function starts with the following code {code}. The description for the function is: {docstring} remove comments; remove summary; remove description; Return only the code
T0T_{0}
T_{0}
T1T_{1}
T_{1}
T2T_{2}
T_{2}

Structural Causal Model

Control

More Context

Multiple Interactions

[case B] Accuracy Results

treatments

potential outcomes

confounders

causal effect

Structural Causal Model

Tprompt=Control,T1,T2T_{prompt} = Control, T_1, T_2
T_{prompt} = Control, T_1, T_2
Y=LevenshteinY = Levenshtein
Y = Levenshtein
Z=SE−MetricsZ = SE-Metrics
Z = SE-Metrics

Research Question

To what extent the type of prompt engineering is influencing the code completion performance?

T0T_{0}
T_{0}
T1T_{1}
T_{1}
T2T_{2}
T_{2}

Structural Causal Model

Control

More Context

Multiple Interactions

Y0≈[0.4±0.2]Y^{0} \approx [0.4 \pm 0.2 ]
Y^{0} \approx [0.4 \pm 0.2 ]

Levenshtein

Y1≈[0.35±0.2]Y^{1} \approx [0.35 \pm 0.2 ]
Y^{1} \approx [0.35 \pm 0.2 ]
Y2≈[0.43±0.2]Y^{2} \approx [0.43 \pm 0.2 ]
Y^{2} \approx [0.43 \pm 0.2 ]
Y0≈0.44Y^{0} \approx 0.44
Y^{0} \approx 0.44

CodeBLEU

Y1≈0.45Y^{1} \approx 0.45
Y^{1} \approx 0.45
Y2≈0.42Y^{2} \approx 0.42
Y^{2} \approx 0.42

Not much variability

[case B] Causal Effects Results

treatments

potential outcomes

confounders

causal effect

Structural Causal Model

Tprompt=Control,T1,T2T_{prompt} = Control, T_1, T_2
T_{prompt} = Control, T_1, T_2
Y=LevenshteinY = Levenshtein
Y = Levenshtein
Z=SE−MetricsZ = SE-Metrics
Z = SE-Metrics

Research Question

To what extent the type of prompt engineering is influencing the code completion performance?

T0T_{0}
T_{0}
T1T_{1}
T_{1}
T2T_{2}
T_{2}

Structural Causal Model

Control

More Context

Multiple Interactions

Y0≈[0.4±0.2]Y^{0} \approx [0.4 \pm 0.2 ]
Y^{0} \approx [0.4 \pm 0.2 ]

Levenshtein

Y1≈[0.35±0.2]Y^{1} \approx [0.35 \pm 0.2 ]
Y^{1} \approx [0.35 \pm 0.2 ]
Y2≈[0.43±0.2]Y^{2} \approx [0.43 \pm 0.2 ]
Y^{2} \approx [0.43 \pm 0.2 ]
Y0≈0.44Y^{0} \approx 0.44
Y^{0} \approx 0.44

CodeBLEU

Y1≈0.45Y^{1} \approx 0.45
Y^{1} \approx 0.45
Y2≈0.42Y^{2} \approx 0.42
Y^{2} \approx 0.42
τ(Lev.)=E[Y1−Y0]=−5.2%\tau (Lev.) = E[Y^1 - Y^0] = -5.2\%
\tau (Lev.) = E[Y^1 - Y^0] = -5.2\%

Treatment 1 Effect

Treatment 2 Effect

τ(Lev.)=E[Y2−Y0]=3.3%\tau (Lev.) = E[Y^2 - Y^0] = 3.3\%
\tau (Lev.) = E[Y^2 - Y^0] = 3.3\%

[case B] Prompt Intervention

Takeaway or Causal Explanation:

 

Elemental context descriptions in the prompt have a negative causal effect on the output with an ATE of -5%. Conversely, prompts with docstrings and signatures have a positive impact on the performance (ATE of 3%)

doCode combines rigorous statistical instruments and causal inference theory to give rise to contextualized SE explanations (of NCMs) using Structural Causal Models (SCMs).

doCode combines rigorous statistical instruments and causal inference theory to give rise to contextualized SE explanations (of NCMs) using Structural Causal Models (SCMs).

 

Moreover, SCMs can provide a more transparent, robust, and explainable approach to Deep Learning for Software Engineering, allowing for a better understanding of the decision-making process of the model and facilitating more effective detection of confounding bias

3. Interventional Interpretability

Challenges and Limitations of doCode

Some challenges practitioners might face when adapting doCode to their interpretability analyses

  • Challenge 1: Proposing a new syntax decomposition function
  • Challenge 2: Collecting data for formulating SE-based interventions
  • Challenge 3: Integrating doCode in DL4SE life-cycle
  • Challenge 4: Creating the Structural Causal Graph

Some general recommendations were performed before proposing the statistical control (Becker et al., 2016)

  • doCode does not control for undocumented confounders
  • doCode uses conceptually meaningful control variables
  • doCode conducts exploratory and comparative analysis to test the relationship between independent and control variables

From Philosophy of Science Perspective

Aspect Pearl (2000, 2009, 2018) Cartwright (1989, 1999, 2007) Bunge (1959, 2003, 2011)
Causal Representation Uses DAGs and do-calculus to model causality. Emphasizes capacities and context-dependent causality. Focuses on real-world systems and deterministic causality.
Intervention-Based Causality Formalized through do(X) operator. Interventions are not always cleanly separable from other factors. Interventions must be understood mechanistically.
Criticism of Do-Calculus Claims causality can be inferred from graphs. Argues DAGs are oversimplifications that ignore real-world complexities. DAGs lack deterministic physical mechanisms.
Application to AI Used in machine learning, fairness, healthcare AI. Suggests AI must be context-sensitive and adaptable. AI should incorporate multi-layered causal structures.

From Philosophy of Science Perspective

Aspect Pearl (2000, 2009, 2018) Cartwright (1989, 1999, 2007) Bunge (1959, 2003, 2011)
Causal Representation Uses DAGs and do-calculus to model causality. Emphasizes capacities and context-dependent causality. Focuses on real-world systems and deterministic causality.
Intervention-Based Causality Formalized through do(X) operator. Interventions are not always cleanly separable from other factors. Interventions must be understood mechanistically.
Criticism of Do-Calculus Claims causality can be inferred from graphs. Argues DAGs are oversimplifications that ignore real-world complexities. DAGs lack deterministic physical mechanisms.
Application to AI Used in machine learning, fairness, healthcare AI. Suggests AI must be context-sensitive and adaptable. AI should incorporate multi-layered causal structures.

4. Counterfactual Interpretability

Autopoietic Architectures

  • [Association] Method 1: TraceXplainer
  • [Association] Method 2: Code Rationales

Rung 1

Rung 2

Rung 3

Association

(correlation)

Intervention

(causation)

Counterfactual

Reasoning

  • [Intervention] Method 3: doCode
  • [Counterfactual] Method 4: Autopoietic Architectures

What about counterfactual interpretability?

The Fundamental Problem of Causal Inference (Holland, 1986)

Q3=P(yt∣t′,y′)Q_3 = P(y_t|t',y')
Q_3 = P(y_t|t',y')

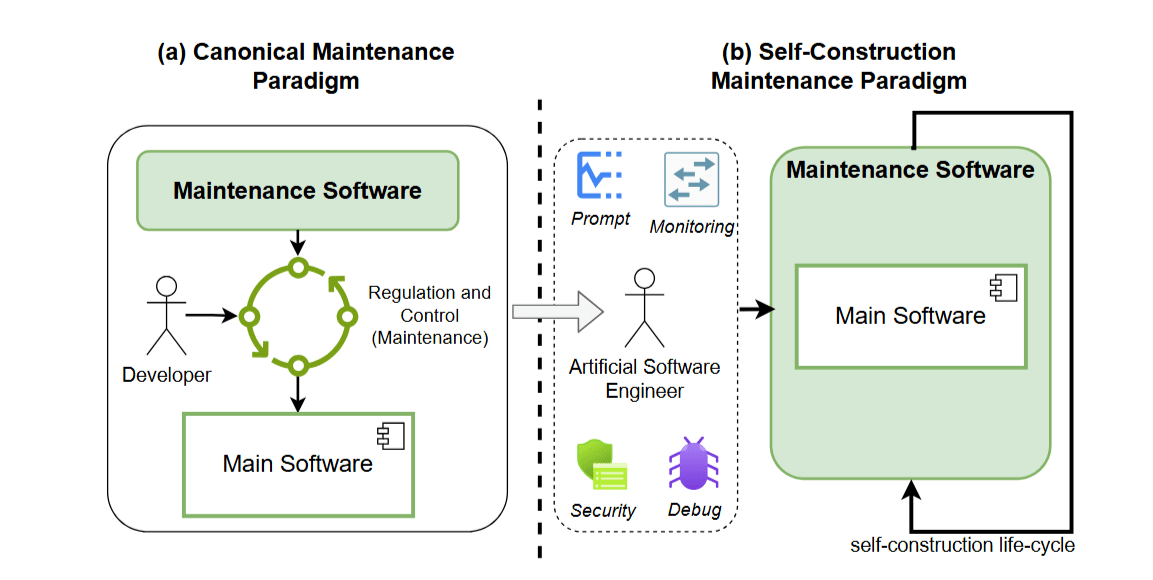
Maintenance Paradigm Shift: a) Software Maintenance (SM) is independent from the main software, and b) SM wraps the main software

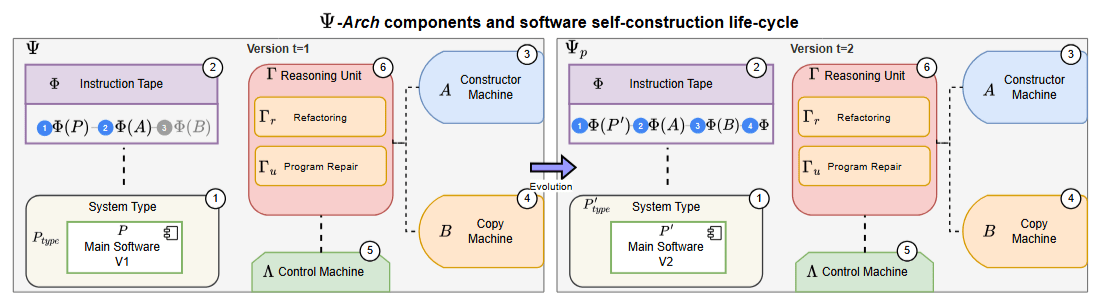
Instead of developing counterfactual interpretability, we envision an autopoietic architecture to enable self-construction of software

Maturana & Varela (1973) + Von Neumann Self-Replication (1966)

5. Consolidation

Future Remarks

Causal Software Engineering

Φ\Phi
\Phi

Prediction

Inference

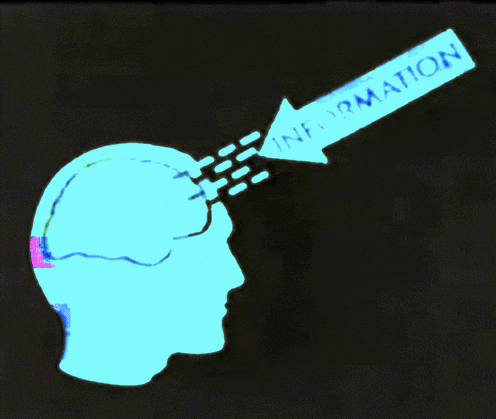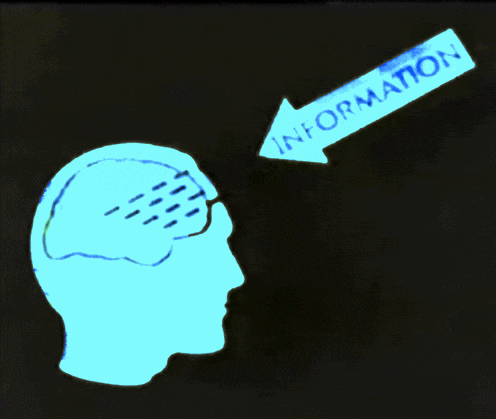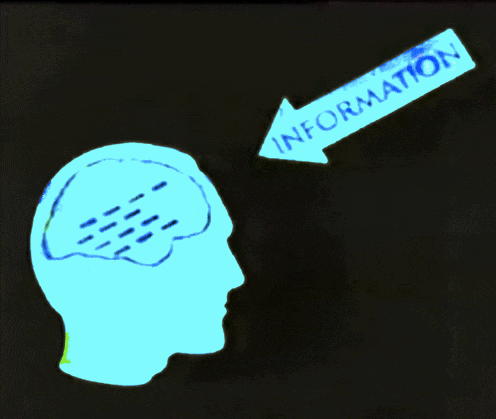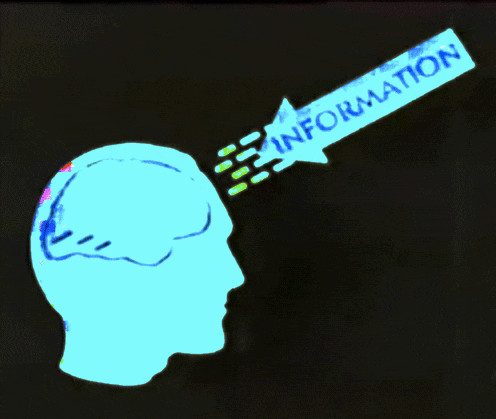
Use the model to predict the outcomes for new data points

Use the model to learn about the data generation process

Prediction

Statistical Inference Methods:

  • Probabilistic Inference or Bayesian Inference
  • Causal Inference

Inference

Learning Process:

  • Machine Learning
  • Deep Learning

The intersection between Causal Inference and Software Engineering is beyond interpretability aspects. It is a whole new science that must be employed to enhance software data analyses (to reduce confounding bias)  and causal discovery (to elaborate explanations)

Causal Software Engineering

Φ\Phi
\Phi

5. Consolidation

Contributions

Contributions Roadmap

Learning to Identify Security Requirements (ICSME'19)

Improving the Effectiveness of Traceability Link Recovery using Bayesian Networks (ICSE'20)

Systematic Review on the use of Deep Learning in SE Research (TOSEM'21)

No Intepretable

Neural Code Models

Observation: Code vs NL modality

Software Artifacts and their relationships can be represented with stocastic variables

Learning to Identify Security Requirements (ICSME'19)

Improving the Effectiveness of Traceability Link Recovery using Bayesian Networks (ICSE'20)

Systematic Review on the use of Deep Learning in SE Research (TOSEM'21)

Toward a Theory of Causation for Interpreting Neural Code Models (TSE'23; ICSE25) 

No Intepretable

Neural Code Models

Observation: Code vs NL modality

Software Artifacts and their relationships can be represented with stocastic variables

Contributions Roadmap

Learning to Identify Security Requirements (ICSME'19)

Improving the Effectiveness of Traceability Link Recovery using Bayesian Networks (ICSE'20)

Systematic Review on the use of Deep Learning in SE Research (TOSEM'21)

Debugging Tool for Code Generation Naural Language Models (Patent'22)

Toward a Theory of Causation for Interpreting Neural Code Models (TSE'23; ; ICSE25) 

No Intepretable

Neural Code Models

Observation: Code vs NL modality

Software Artifacts and their relationships can be represented with stocastic variables

Feature Importance Technique: Code Rationales

Evaluating and Explaining Large Language Models for Code Using Syntactic Structures (Preprint'24) 

A formalism for Syntax Decomposition

Which Syntactic Capabilities Are Statistically Learned by Masked Language Models for Code? (ICSE'23) 

Benchmarking Causal Study to Interpret Large Language Models for Source Code (ICSME'23) 

CodeBert Negative Results (not learning syntax)

Prompt Engineering Evaluation

Conjecture:

Software Information exhibits causal properties

Contributions Roadmap

"T causes Y if Y listens to T". That is, if we change T, we also have to observe a change in Y (Pearl, 2019)

Causal Agents can interact with the (software) environment

Artificially Engineering

Software Systems

Code Generator

Causal Reasoning

Unit

self-replication

Evolved Agent

Replication Unit

Perception Unit

Controller

 Requirement Generator

Causal Reasoning

Unit

Replication Unit

Perception Unit

Controller

SE Agents or Autopoietic Arch

software information: req

causal queries

Learning to Identify Security Requirements (ICSME'19)

Improving the Effectiveness of Traceability Link Recovery using Bayesian Networks (ICSE'20)

Systematic Review on the use of Deep Learning in SE Research (TOSEM'21)

Debugging Tool for Code Generation Naural Language Models (Patent'22)

Toward a Theory of Causation for Interpreting Neural Code Models (TSE'23) 

No Intepretable

Neural Code Models

Observation: Code vs NL modality

Software Artifacts and their relationships can be represented with stocastic variables

Feature Importance Technique: Code Rationales

Evaluating and Explaining Large Language Models for Code Using Syntactic Structures (Preprint'24) 

A formalism for Syntax Decomposition

Which Syntactic Capabilities Are Statistically Learned by Masked Language Models for Code? (ICSE'23) 

Benchmarking Causal Study to Interpret Large Language Models for Source Code (ICSME'23) 

CodeBert Negative Results (not learning syntax)

Prompt Engineering Evaluation

Software Agents

Contributions Roadmap

Causal Software Eng.

Gracias!

[Thank you]

Traditional Interpretability

  • Inherently interpretable models:
    • Decision Trees
    • Rule-based models
    • Linear Regression
    • Attention Networks
    • Disentangled Representations
  • Post Hoc Explanations:
    • SHAP
    • Local Interpretable Model-Agnostic Explanations (LIME)
    • Saliency Maps
    • Example-based Explanations
    • Feature Visualization

Causal Interpretability

Approaches that follow Pearl's Ladder

  • Average Causal Effect of the neuron on the output (Chattopadhyay et, al., 2019)
  • Causal Graphs from Partial Dependence Plots (Zhao & Hastie, 2019)
  • DNN as an SCM (Narendra et al., 2018)

[case C] Syntax Decomposition on Encoder-Only experiment setup. 

Q=P(Y∣do{T})Q = P(Y|do\{T\})
Q = P(Y|do\{T\})
docodedo_{code}
do_{code}
p(wt∣w1...t−1)p(w_t|w_{1...t-1})
p(w_t|w_{1...t-1})

autoregressive

extract interpretability features

code completion logits

feasible completions

causal explanations

method 3

Structural Causal Model (SCM)

How good are MLMs at predicting AST nodes?

CodeBERT

Neural Code Models

Testbed: GALERAS

[case C] Structural Causal Graph proposed (graph hypothesis)

treatments

potential outcomes

confounders

causal effect

Structural Causal Model

Tprompt=Control,TconceptT_{prompt} = Control, T_{concept}
T_{prompt} = Control, T_{concept}
Y=JaccardY = Jaccard
Y = Jaccard
Z=SE−MetricsZ = SE-Metrics
Z = SE-Metrics

GALERAS

Token Prediction

Static Tools

Research Question

How good are MLMs at predicting AST nodes?

T0T_{0}
T_{0}
TconceptT_{concept}
T_{concept}

Structural Causal Model

Control

AST Node Types

[case C] Results

treatments

potential outcomes

confounders

causal effect

Structural Causal Model

Tprompt=Control,TconceptT_{prompt} = Control, T_{concept}
T_{prompt} = Control, T_{concept}
Y=JaccardY = Jaccard
Y = Jaccard
Z=SE−MetricsZ = SE-Metrics
Z = SE-Metrics

Research Question

How good are MLMs at predicting AST nodes?

Structural Causal Model

Local Jaccard

[case C] Syntax Decomposition Encoder-Only

Takeaway or Causal Explanation:

 

CodeBERT tent to complete missing AST-masked tokens with acceptable probability (>0.5). However, the reported performance suffers from high variability (+- 0.21) making the prediction process less confident compared to completing randomly masking tokens.

Source File

Requirement File

Test File

Test File

θ=?\theta = ?
\theta = ?
Exec2Exec_2
Exec_2
Exec1Exec_1
Exec_1
θ1\theta_1
\theta_1
θ2\theta_2
\theta_2

Do we use Inference or Prediction to compute θ?

Causal Interpretability [Pre-Defense]

By David Nader Palacio

Causal Interpretability [Pre-Defense]

Discover innovative approaches to enhance the interpretability of deep learning in software engineering. Explore groundbreaking insights that promise to transform the field and foster a deeper understanding of complex models. Join us on this exciting journey!

  • 25

More from David Nader Palacio