Trie
LAB 14
B4M33PAL - Ing. David Pařil
Trie
Trie
Binární
0
1
10011
10010
0
1
0
1
0
0
1
0
1
01000
00101
00011
00001
0
1
Příklad binární trie:
Příklad
Binární trie
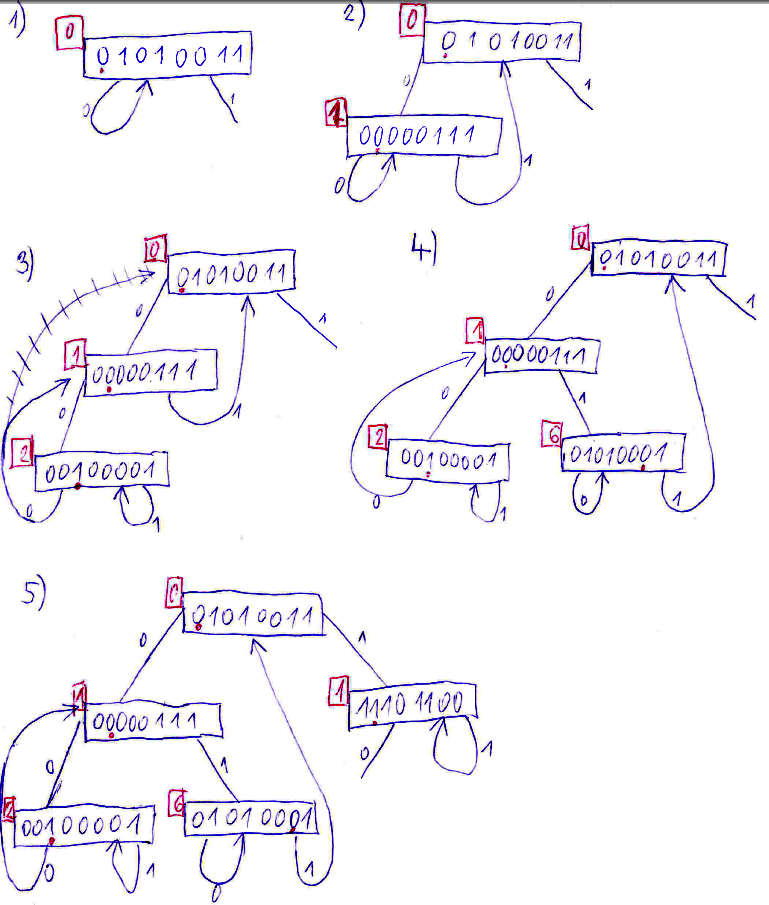
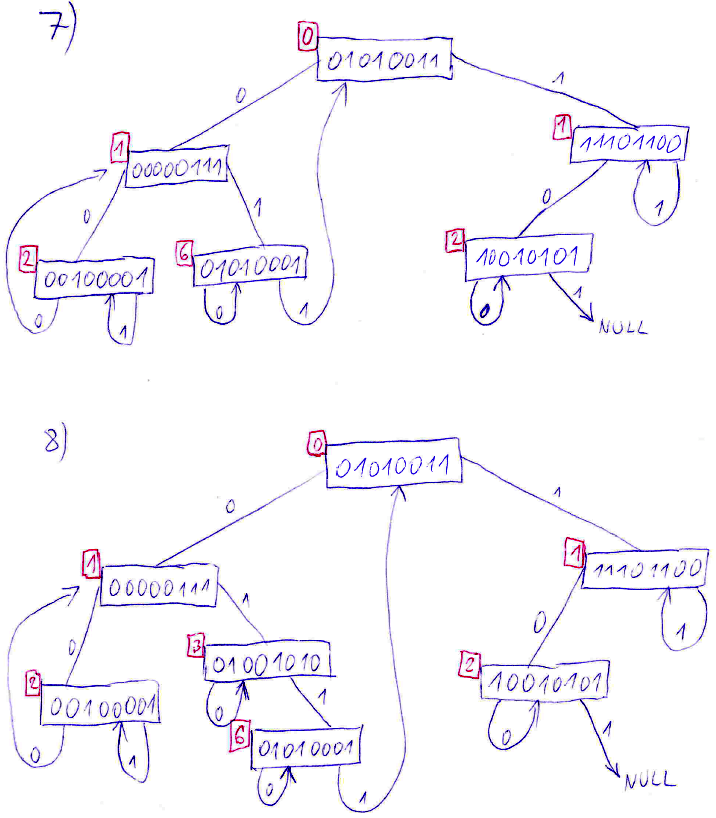
Vybudujte binární trie tak, že do něj postupně vložíte klíče:
1.
2.
3.
4.
5.
6.
7.
8.
10010101
11101100
00000111
00100001
01001010
01010001
01010011
00100001
01010011
10010101
11101100
00000111
00100001
01001010
01010001
00100001
0
0
1
00000111
01010011
10010101
11101100
00100001
01001010
01010001
00100001
0
0
0
1
1
01010011
00000111
00100001
10010101
11101100
01001010
01010001
00100001
0
0
0
1
1
0
1
0
0
0
1
00000111
00100001
01010001
01010011
10010101
11101100
01001010
00100001
0
0
0
1
1
0
1
0
0
0
1
1
11101100
00000111
00100001
01010001
01010011
10010101
01001010
00100001
0
0
0
1
1
0
1
0
0
0
1
1
11101100
00000111
00100001
01010001
01010011
Kolize
10010101
01001010
00100001
0
0
0
1
1
0
1
0
0
0
1
1
0
1
10010101
11101100
00000111
00100001
01010001
01010011
01001010
0
0
0
1
1
0
0
1
0
0
0
1
1
0
1
10010101
11101100
00000111
00100001
01001010
01010001
01010011
Hotovo 😎👍️
Příklad
Minimální bin. trie
Nakreslete příklad binární trie, která obsahuje 6 klíčů, každý o 5 bitech.
Trie bude obsahovat klíče:
Hloubka trie bude minimální možná.
1.
2.
00000
11111
0
0
0
1
1
1
0
1
0
1
01010
10101
00000
00111
11000
11111
Jak jsme k tomu došli?
Potřebujeme 6 listů \(\rightarrow\) strom s hloubkou \(h\) má maximálně \(2^h\) listů.
Minimální možná hloubka je tedy 3.
Aby trie nemusela dělat dlouhé „one-way“ řetězce, musí se klíče lišit brzy.
Už na 1. bitu rozdělíme na poloviny (prefix 0xxxx a 1xxxx)
Příklad
TODO
Určete, kolik minimálně a kolik maximálně paměti je zapotřebí pro uložení binární trie obsahující
1 000 000 řetězců,
z nichž každý má délku 50 ASCII znaků.
Příklad
bitové doplňky
V daném binarní trie chceme nahradit každý klíč jeho bitovým doplňkem.
Navrhněte efektivní postup, který to provede bez budování nového trie a rušení starého.
Jaká bude asymptotická složitost vaší metody?
0
0
0
1
1
0
0
1
0
0
0
1
1
0
1
10010101
11101100
00000111
00100001
01001010
01010001
01010011
0
0
0
1
1
1
0
1
1
1
0
1
1
0
1
10010101
11101100
00000111
00100001
01001010
01010001
01010011
11111000
11011110
10110101
10101110
10101100
01101010
00010011
Co se právě stalo?
Prohodili jsme "levé" a "pravé" větve
Každý list jsme nahradili jeho doplňkem

But at what cost?
Asymptotická složitost
🍅 = počet uzlů v trie
🥦 = počet listů = počet klíčů
🥒 = délka klíčů
- Průchod stromem \(O(🍅)\)
- Swap je \(O(1)\)
- Přepis klíčů v listech \(O(🥦\cdot🥒)\)
Celkem:
$$ O(🍅 + 🥦 \cdot 🥒) $$
Protože 🥦 \(\leq\) 🍅, můžeme zapsat:
$$ O(🍅 \cdot 🥒) $$
Příklad
Mergování trie
Máme dva binární trie \(T1\) a \(T2\) a je zaručeno že celkově obsahují unikátní klíče.
Je možné sestavit metodu Merge(T1, T2), která spojí oba trie do jediného nového binárního trie a přitom nevytváří ani neruší žádné existující uzly v obou triích?
Pokud ano, napište pseudokód.
0
0
0
0
1
1
1
0
1
1
100111
001011
010110
011001
000000
000101
0
0
0
0
1
1
1
0
1
1
100110
001010
010111
011000
000001
000100
Příklad:
0
0
0
0
0
0
1
1
0
0
1
1
0
1
0
1
1
0
1
1
0
1
1
0
0
0
1
1
0
0
1
1
0
1
000000
000001
000100
000101
001010
001011
010110
010111
011000
011001
100110
100111
Řešení:
Bohužel nám vznikly nové vnitřní uzly...
Takže ne - nelze takový algoritmus udělat...
zadání je totiž špatně napsané 😅
Příklad
Mergování trie - pokus druhý
Máme dva binární trie \(T1\) a \(T2\) a je zaručeno že celkově obsahují unikátní klíče.
Je možné sestavit metodu Merge(T1, T2), která spojí oba trie do jediného nového binárního trie a přitom nevytváří ani neruší žádné existující uzly v obou triích?
Pokud ano, napište pseudokód.
listy 🌿
moc dlouhé
Řešení
DFS současně v obou trie.
Když narazím na list v T1 a v T2 je podstrom, tak:
- ten podstrom přesunu,
- a pak do něj vložím nalezený listový klíč (což může vytvořit nové vnitřní uzly).
Když narazím na list v T2, tak ho přesunu z T2 a vloží do T1 na odpovídající místo (zase může vzniknout vnitřní uzel).
Příklad
smazání klíče
Napište pseudokód smazání klíče v binárním trie.

Obrázek: Daieny Schuttz: Oozora Subaru (hololive Production / Cover Corp)
Řešení:
- Jdi podle bitů dolů stromem
- V listu ověř, že je to opravdu hledaný klíč
-
Odpoj list se smazaným klíčem
- Cestou zpět uklízej zbytečné vnitřní uzly
function Delete(ref t, K, d):
if t == null: return false
if IsLeaf(t):
if t.key != K: return false
t = null // smaž list
return true
b = digit(K, d)
if b == 0: ok = Delete(t.left, K, d+1)
else: ok = Delete(t.right, K, d+1)
if not ok: return false
// úklid po smazání:
if t.left == null and t.right == null:
t = null // vnitřní uzel zbytečný
else if t.left == null:
t = t.right // bypass (má jen pravé dítě)
else if t.right == null:
t = t.left // bypass (má jen levé dítě)
return true
// volání:
Delete(root, K, 0)
Příklad
TODO
Do binárního trie chceme přidat posloupnost klíčů \(k_1, k_2, ..., k_N\).
Víme přitom, že každý další klíč v posloupnosti má hodnotu o 1 větší než přechozí klíč ( např. 0110, 0111, 1000, 1001, 1010, apod).
Je zaručeno že původní trie neobsahuje žádný z přidávaných klíčů.
Rozhodněte, zda to lze učinit rychleji, než postupným přidáváním jednotlivých klíčů do původního trie.
P
A
T
R
I
C
I
A
Trie
P
A
T
R
I
C
I
A
Trie
ractical
lgorithm
o
etrieve
nformation
oded
n
lphanumeric
Neplýtvá uzly na místech,
kde se nic nevětví 😎
S 10011
0
H 01000
1
E 00101
2
C 00011
3
A 00001
4
S 10010
4
Příklad:
Hledáme R = 10010
- Jdeme vpravo, protože bit 0 je 1
- Poté doleva, protože bit 4 je 0
- To nás dovede k R (uzel S)
S 10010
S 10011
0
H 01000
1
E 00101
2
C 00011
3
A 00001
4
S 10010
4
Příklad:
Hledáme I = 01001
- Jdeme vlevo, protože bit 0 je 0
- Jdeme vpravo, protože bit 1 je 1
- Nalezneme H, což ale není I
(vyhledávání bylo neúspěšné)
H 01000
S 10011
0
H 01000
1
E 00101
2
C 00011
3
A 00001
4
S 10010
4
3 hlavní vlastnosti Patricie:
- nemá null linky
- testujeme uvedený bit místo následujícího
- končíme když vylezeme stromem nahoru
H 01000
Insert
- Najdeme nejpodobnější klíč (nevkládáme pokud je stejný)
- Najdeme první bit z leva, v kterém se klíče liší
- Pak rekurzivně voláme funkci
insertR...
Mohou nastat 2 případy:- Nový uzel nahradí interní spojení
- Externí spojení
0
S 10011
1
H 01000
2
E 00101
3
C 00011
4
A 00001
4
S 10010
2
N 01110
4
I 01001
0
S 10011
1
H 01000
2
E 00101
3
C 00011
4
A 00001
4
S 10010
4
N 01001
Příklad
Patricia Trie
Vybudujte patricia trie tak, že do něj postupně vložíte klíče:
1.
2.
3.
4.
5.
6.
7.
8.
10010101
11101100
00000111
00100001
01001010
01010001
01010011
00100001
0
10010101
11101100
00000111
00100001
01001010
01010001
00100001
01010011
0
1
10010101
11101100
00100001
01001010
01010001
00100001
0
00000111
01010011
1
1
0
0
1
0
10010101
11101100
00000111
00100001
01001010
01010001
00100001
01010011
1
1
0
0
1
2
1
0
0
10010101
11101100
00000111
00100001
01001010
01010001
00100001
01010011
1
1
0
0
1
2
1
0
3
0
1
0
10010101
11101100
00000111
00100001
01001010
01010001
00100001
01010011
1
1
0
0
1
2
1
0
3
2
1
0
0
1
0
10010101
11101100
00000111
00100001
01001010
01010001
00100001
01010011
1
1
0
0
1
2
1
0
3
2
1
0
0
1
0
10010101
11101100
00000111
00100001
01001010
01010001
01010011
1
1
0
0
1
2
1
0
3
2
1
0
1
1
0
1
0
0
10010101
11101100
00000111
00100001
01001010
01010001
01010011
1
1
0
0
1
2
1
0
3
2
1
0
1
1
1
1
0
0
4
Příklad
TODO
Nakreslete příklad patricia trie, která obsahuje 6 klíčů, každý o 5 bitech.
Trie bude obsahovat klíče:
Hloubka trie bude minimální možná.
1.
2.
00000
11111
00100
00001
00000
10001
2
4
0
1
Řešení
Vkládáme klíče: 00000, 00100, 10001, 00111, 11111, 00001 (v tomto pořadí)
0
0
11111
2
1
1
00111
2
1
1
1
1
0
Na
Viděnou
už nikdy :(
Friendly reminder:
Přihlašte se na praktickou část zkoušky:

Viz: https://cw.fel.cvut.cz/wiki/courses/b4m33pal/zkouska


Předmětová Anketa ČVUT

Kupte si Merch

Nově jsme i na fiverru!

Zkouškové testy a další bonusový obsah
Bonusový Příklad
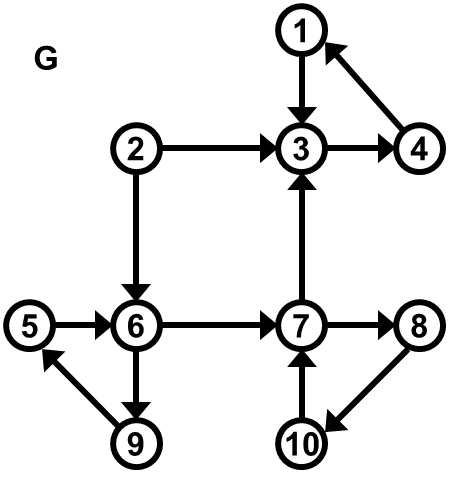
:)
Orientovaný graf G na obrázku má 10 vrcholů označených 1, 2, ..., 10. Tarjanův algoritmus zpracovává G a začne ve vrcholu 2. Algoritmus při své činnosti postupuje dopředu do dosud neotevřených vrcholů vždy tak, že pokaždé v určitém vrcholu vybírá jeho sousední vrchol s nejnižším možným označením.
- Kolik silně souvislých komponent obsahuje G?
- V jakém pořadí budou detekovány jednotlivé silné komponenty G?
- Předpokládejme, že funkčnost Tarjanova algoritmu je rozšířená o proceduru, která při každé detekci silně souvislé komponenty projde všechny dosud detekované silně souvislé komponenty v čase úměrném celkovému počtu hran v těchto komponentách. Jaká bude asymptotická složitost výsledného algoritmu za předpokladu, že graf má \(n\) vrcholů a \(m\) hran?
A
B
H
I
C
G
D
E
F
4
8
7
9
10
14
4
2
1
8
11
7
2
6

B
B
B
Díky za super
14 cvičení :)
Klidně piště na: parildav@fel.cvut.cz

PAR_Lab14
By David Pařil
PAR_Lab14
- 25


