Part I. Water Problems
Water Problems(Warm up)
今天要讲的本来就很水, 这个部分更水啦. 不过感觉还比较有趣的样子.
似乎都是几道跟排序的交换次数有关的水题.
那么现在就开始吧.
[NOIp2013]火柴排队 · 改
给你一个序列 A, 允许交换相邻的两个元素, 求最少交换次数使得其变为非降序.
Solution
逆序对.
冒泡排序的交换次数好像就是这么多.
[CF #277.5 Div.2 A]SwapSort · 改
给你一个序列 A, 允许交换任意的两个元素, 求最少交换次数使得其变为非降序
Solution
数据变大了, 原题的那种做法不行了.
不妨给 A 先排个序, 然后找环. 因为元素个数为 m 的环只需交换 m - 1 次, 故最后答案等于 N 减去总环数.
[我口胡的]OOOO
给你一个序列 A, 允许移动一个元素至任意元素的前后, 求最少移动次数使得其变为非降序.
Solution
最长不降子序列.
答案等于 N 减去最长不降子序列的长度.
[我口胡的]OOOO · 改
给你一个序列 A, 为 1 到 N 的某个排列. 允许移动一个元素至序列的头或尾, 求最少移动次数使得其变为非降序.
Solution
最长等差数列. (这个递推就好了)
答案等于 N 减去最长的公差为1的等差数列的长度.
似乎有一道类似一样的面试题.
Part II. Dancing Links
[HUSTOJ1017]Exact cover
给定一个 N * M 矩阵, 求出一个可行的行的集合使得每个列都被 1 覆盖恰好一次.
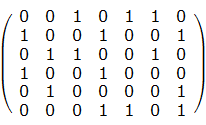
上图的解为 {1, 4, 5} 行.
每行的 1 不超过 100 个.
显然暴搜嘛......
但是显然超时嘛......
Solution?
考虑优化暴搜. 可以发现这是一个稀疏矩阵, 而普通暴搜在一个 N* M 的数组上搜索太浪费了.
不妨对比图论的邻接矩阵与邻接表, 后者在稀疏图中比前者优; 是不是此类题目也可以利用链表优化呢?
感觉可以, 不过有个问题, 如何快速回溯(恢复)?
这就要用到舞蹈链(Dancing Links)了.
暂时不考虑舞蹈链的问题, 先假设我们拥有一种能快速删除和恢复的数据结构, 看看搜索过程中具体需要哪些操作.
如果 A 为空, 返回成功
否则, 选择一个列 c
枚举每个使得 A[r][c] = 1 的行 r
对于每一个使得 A[r][j] = 1 的列 j
从 A 中删除列 j
对于每一个使得 A[i][j] = 1 的行 i
从 A 中删除行 i
在不断变小的 A 上递归
恢复之前被删除的行与列(回溯)
返回失败就是一个很普通的回溯嘛...... 但是, 如果用标记数组什么的来实现, 对于稀疏矩阵很浪费有没有.
Overview
舞蹈链是一种数据结构, 可以快速地操作和回溯(删除和恢复).
它实质上是一个双向链表. 准确的说是"交叉十字循环双向链"
就像这样:
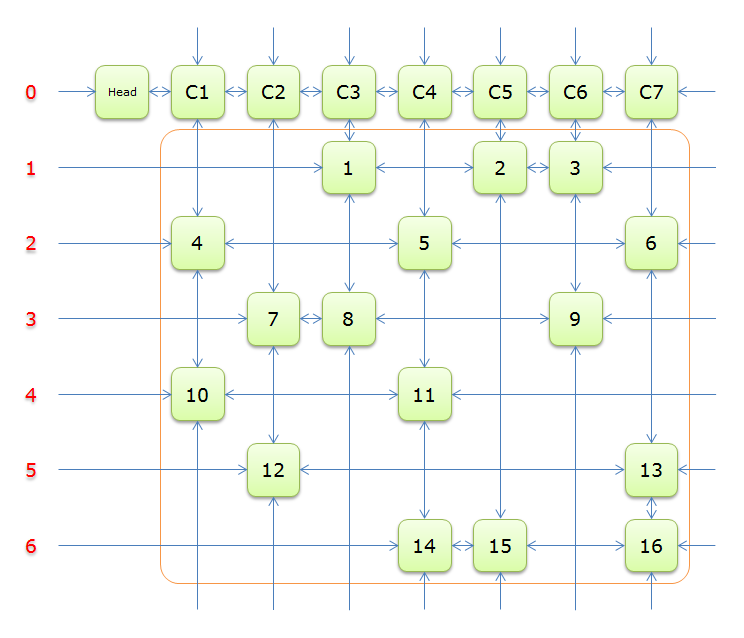
Dancing Links
是不是看上去很简单?
快速删除和恢复基于以下事实:
L[R[x]]←L[x],R[L[x]]←R[x]同时可以通过如下操作快速恢复 x:
L[R[x]]←x, R[L[x]]←x是不是很显然. 舞蹈链的核心就是这个.
Dancing Links
在双向链表中, 删去一个节点 x 的操作是
Dancing Links
将矩阵 A 中的每个元素 1 用五个值 L[x], R[x], U[x], D[x], C[x] 来表示. 矩阵的每行都是一个环形的双向链表, 通过L,R两个域连通; 每一列也是一个环形的双向链表, 通过U,D两个域连通.

还是这张图......
L, R 是左右的链;
U, D 是上下的链;
让我们模拟一下删除和恢复操作.
Dancing Links
实现很简单, 白书上已经讲的很清楚了.
你也可以去看我的博客.
你可能会觉得, 这个东西原理好简单, 但怎么实现呢?
[POJ3076]Sudoku
求解一个 16 * 16 的数独, 保证有唯一解.
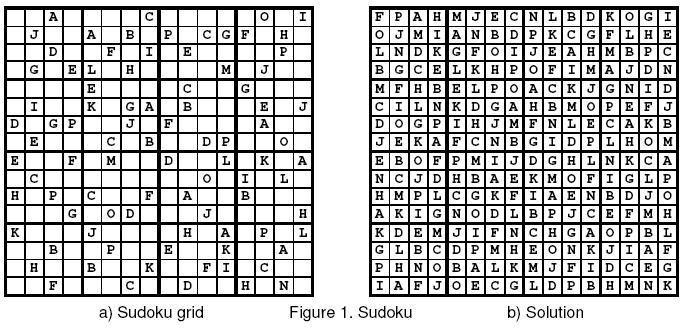
Solution
既然讲了舞蹈链, 那么肯定用它来优化嘛......
很容易转化, 不放枚举每个格子 (r, c) 放的数字 x, 则约束为:
- r 行 c 列上有数字 → 16 * r + c 列为 1
- r 行上有数字 x → 16 * r + x + 256 列为 1
- c 列上有数字 x → 16 * c + x + 512 列为 1
- s 子方阵里有数字 x → 16 * s + x + 768 列为 1
若格子初始已经填了数字则不用枚举.
于是 16 * 16 的数独被转化成一个共 4096 行, 1024 列, 并且每行 1 的个数为 4 的精确覆盖问题.
直接套模板.
Optimization
舞蹈链毕竟还是暴搜...... 怎么能不优化.
对舞蹈链的通(sha)用(bi)优化:
- 维护每一列当前 1 的个数, 每次选择 1 最少的列搜索. (这也能叫优化?)
对数独问题的优化:
- 构造矩阵时通过标记数组之类的方式可以去掉很多不可能合法的状态.
差不多就是这些了吧......
Water Problems and Dancing Links
By debug18
Water Problems and Dancing Links
- 1,668