Aprendizaje por refuerzo aplicado al problema de pastoreo

Índice de Contenidos

1. Aprendizaje por refuerzo

2. Problema de Pastoreo

1. Aprendizaje por refuerzo

1. Aprendizaje por refuerzo

Q -Learning

\(\displaystyle \mathcal{Q}(s_t,a_t) \gets (1-\alpha)\mathcal{Q}(s_t,a_t) + \big[ r(s_t,a_t) + \gamma \max_{a'\in \mathcal{A}}\mathcal{Q}(s_{t+1},a') \big] \)

1. Aprendizaje por refuerzo

1.1 Proceso de desición de Markov

1.2 Programación dinámica

1.3 Algoritmos de aprendizaje por Refuerzo

1.1 Proceso de desición de Markov

 1.1 Proceso de desición de Markov

Definición

1. Una variable aleatoria  \( S_t \in \mathcal{S}\)

2. Una variable aleatoria \( A_t \in \mathcal{A}\)

3. Una variable aleatoria \( R_t \in \mathcal{R}\)

4. Distribución de probabilidad:

\( \mathbb{P}(S_t=s',R_t=r|S_{t-1},A_t=a) = p_t (s',r|s,a)\) 

 1.1 Proceso de desición de Markov

Definición

1. Una variable aleatoria  \( S_t \in \mathcal{S}\)

2. Una variable aleatoria \( A_t \in \mathcal{A}\)

3. Una variable aleatoria \( R_t \in \mathcal{R}\)

4. Distribución de probabilidad:

Si \(S_t\)  y \(R_t\) son independientes, entonces:

\( p (s',r|s,a) = p_t(s'|s,a) p_r(r|s,a)\) 

 1.1 Proceso de desición de Markov

Ejemplo

1. Una variable aleatoria \( S_t \in \{ s_1,s_2,\dots,s_{11}\}\)

2. Una variable aleatoria \( A_t \in \{ \rightarrow,=,\leftarrow\}\)

3. Una variable aleatoria \( R_t \in \mathcal{R} \)

\( \mathbb{P}(R_t=r|S_{t-1}=s,A_t=a) = p_r(r|s,a) = \delta(r,f_r(s,a))\)

\( \)

Donde \(f_r(s,a)\) es:

 1.1 Proceso de desición de Markov

Ejemplo

4. Una funcion de transición \(     p_t(s'|s,a) \)

Donde \(f_s(s,a)\) es:

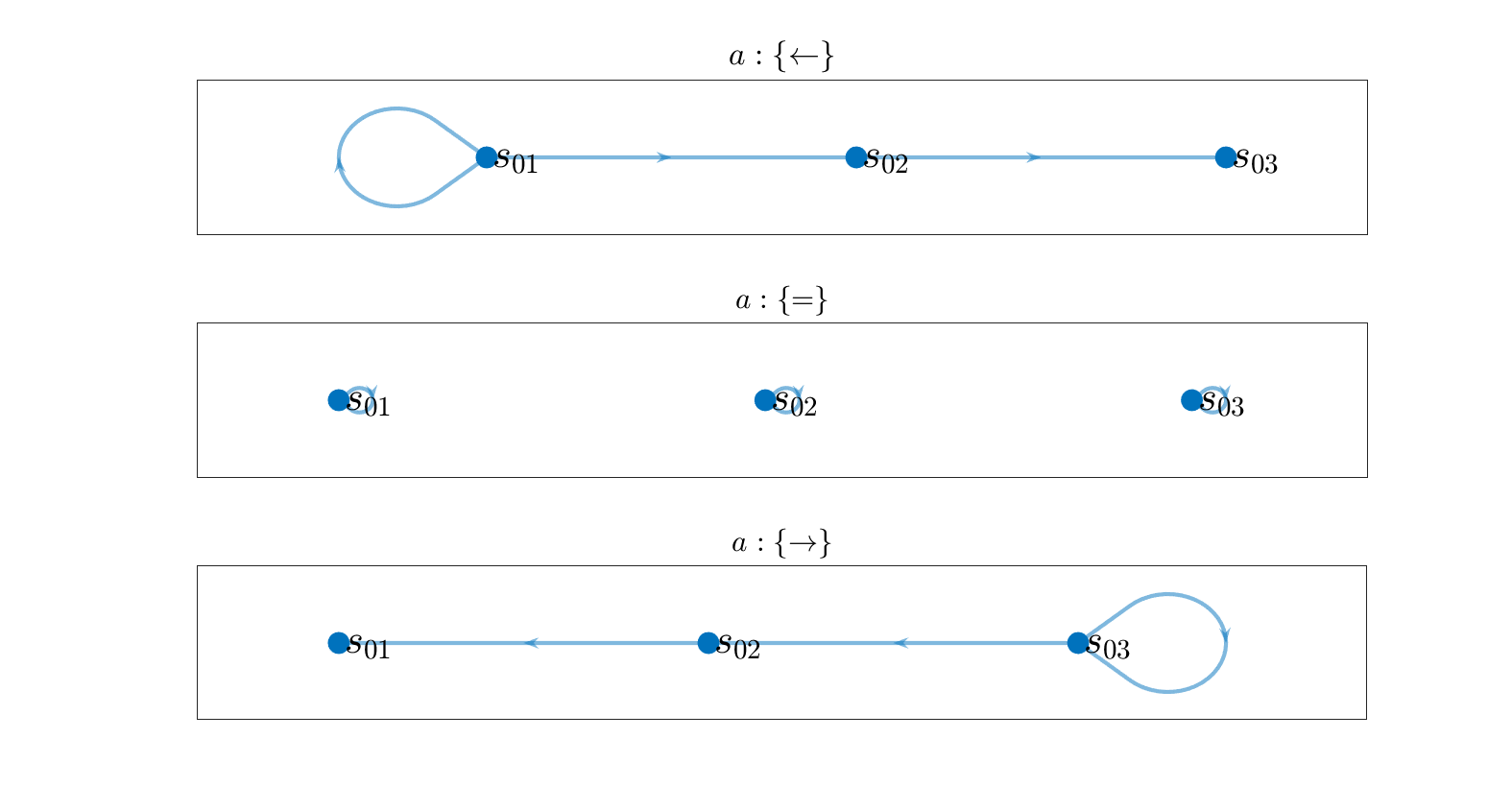
 1.1 Proceso de desición de Markov

Ejemplo

 1.1 Proceso de desición de Markov

Política (\(\pi \))

Es una función \(\pi:\mathcal{S} \rightarrow \mathcal{A} \), que determina las acciones que se tomarán

Dado \( s \in \mathcal{S}\) mazimizamos de la recompensa esperada

Objetivo

Política óptima (\(\pi_*\))

1.2 Programación dinámica

 1.2 Programación dinámica

Funcion valor de estado óptima

        \( \displaystyle v_*(s) = \max_{\pi\in \Pi}  \mathbb{E}_\pi \big[\sum_{t=0}^\infty \gamma^\tau R_{{\tau+1}}|S_0=s \big]\)

Política óptima (\(\pi_*\))

\( \displaystyle  \pi_*(s) \in \arg \max_{\pi \in \Pi} v_*(s) \)

 1.2 Programación dinámica

Funcion valor de estado óptima

        \( \displaystyle v_*(s) = \max_{\pi\in \Pi}  \mathbb{E}_\pi \big[\sum_{t=0}^\infty \gamma^\tau R_{{\tau+1}}|S_0=s \big]\)

Ecuación de Bellman Óptima

\( \displaystyle   v_*(s) = \max_{a} \bigg[ \rho(s,a) + \gamma \sum_{s'}p_t(s'|s,a) v_*(s') \bigg]\)

Donde \( \rho(s,a)\) es:

\( \rho(s,a) = \mathbb{E}[R_t |S_{t-1}=s,A_t=a]\) 

 1.2 Programación dinámica

Funcion valor de estado óptima

        \( \displaystyle v_*(s) = \max_{\pi\in \Pi}  \mathbb{E}_\pi \big[\sum_{t=0}^\infty \gamma^\tau R_{{\tau+1}}|S_0=s \big]\)

Ecuación de Bellman Óptima

\( \displaystyle   v_*(s) = \max_{a} \bigg[ \rho(s,a) + \gamma \sum_{s'}p_t(s'|s,a) v_*(s') \bigg]\)

Operador de Bellman Óptimo

\( \displaystyle \mathcal{T}_v \mathcal{V}(s) = \max_{a\in\mathcal{A}} \bigg[ \rho(s,a) + \gamma \sum_{s' \in \mathcal{S}} p_t(s'|s,a) \mathcal{V}(s') \bigg]\)

 1.2 Programación dinámica

Teorema de Punto Fijo

1. El operador \(\mathcal{T}_v\) tiene un punto fijo que es \(v^*\)

\(\mathcal{T}_v v^* = v^* \)

2. Existe la contracción en la norma \( L ^\infty\)

\( ||\mathcal{T}_v \mathcal{V}_1 -  \mathcal{T}_v \mathcal{V}_2 ||_{\infty} \leq  \gamma || \mathcal{V}_1 -  \mathcal{V}_2 ||_{\infty}\)

Entonces, si aplicamos de manera consecutiva el operador \(\mathcal{T}_v \) a cualquier función \( \mathcal{V} \),  convergeremos al punto fijo \( v^*\)

 1.2 Programación dinámica

Value Iteration (\(\mathcal{V}^*,tol\))

         \(k \leftarrow 0\)

         \(\mathcal{V}_k \leftarrow \mathcal{V}^*\)

         While \(error \leq tol\) do

                \( k \leftarrow k + 1\)

                \(\mathcal{V}_{k} \leftarrow \mathcal{T}_v \mathcal{V}_{k-1}\)

                \(error \leftarrow || \mathcal{V}_k - \mathcal{V}_{k-1}||_{\infty}\)

          end while

         \(\displaystyle \pi_k(s) = \argmax_{a \in \mathcal{A}}    [\rho(s,a) + \gamma \sum_{s'} p(s'|s,a) \mathcal{V}_k(s')\)

         return [\(\mathcal{V}_k(s),\pi_k^*(s)\)]

end

 1.2 Programación dinámica

Funcion valor de estado-accion óptima

        \( \displaystyle q_*(s,a) = \max_{\pi\in \Pi}  \mathbb{E}_\pi \big[\sum_{t=0}^\infty \gamma^\tau R_{{\tau+1}}|S_0=s,A_0=0\big]\)

Ecuación de Bellman Óptima

\( \displaystyle   q_*(s,a) = \bigg[ \rho(s,a) + \gamma  \sum_{s'}p_t(s'|s,a) \max_{a' \in \mathcal{A}}q_*(s',a') \bigg]\)

Operador de Bellman Óptimo

\( \displaystyle \mathcal{T}_q \mathcal{Q}(s,a) =  \bigg[ \rho(s,a) + \gamma \sum_{s' \in \mathcal{S}} p_t(s'|s,a)\max_{a'\in\mathcal{A}} \mathcal{Q}(s',a') \bigg]\)

 1.2 Programación dinámica

Q Iteration (\(\mathcal{Q}^*,tol\))

         \(k \leftarrow 0\)

         \(\mathcal{Q}_k \leftarrow \mathcal{Q}^*\)

         While \(error \leq tol\) do

                \( k \leftarrow k + 1\)

                \(\mathcal{Q}_{k} \leftarrow \mathcal{T}_q \mathcal{Q}_{k-1}\)

                \(error \leftarrow || \mathcal{Q}_k - \mathcal{Q}_{k-1}||_{\infty}\)

          end while

         \(\displaystyle \pi_k(s) = \argmax_{a \in \mathcal{A}}   \mathcal{Q}_{k}(s,a)\)

         return [\(\mathcal{Q}_k(s,a),\pi_k^*(s)\)]

end

 1.2 Programación dinámica

Ejemplo

Estado y Acción

\( s = [x_t,v_t] \ \ |\ \ x \in [-6,6] \ \& \ \ v \in [-6,6] \)

\( a\in \{ -10,0,10\}\)

Dinámica

Recompensa

 1.2 Programación dinámica

 1.2 Programación dinámica

Donde \(A\) y \(B\) son las matrices jacobianas de \(f\) con respecto al estado \(s=[x,v]\) y la acción \(a\), evaluados en \(s=[0,0]\) y \(a=0\).

Este control tipo es llamado regulador cuadrático linear (LQR) .

Comparación con control óptimo LQR

 1.2 Programación dinámica

Comparación con control óptimo LQR

 1.2 Programación dinámica

Value Iteration

 1.2 Programación dinámica

Value Iteration

1.3 Algoritmos de Aprendizaje por refuerzo

 1.3 Aprendizaje por Refuerzo

Aprendizaje por refuerzo

Los operadores de Bellman necesitan recorrer todo el \( \mathcal{S}\)/\(\mathcal{A}\)

\(\mathcal{Q}_{k} \leftarrow \mathcal{T}_q \mathcal{Q}_{k-1}\)

\(\mathcal{V}_{k} \leftarrow \mathcal{T}_v \mathcal{V}_{k-1}\)

En Aprendizaje por refuerzo NO conocemos la dinámica

\(p(s_t, r_t|s_{s-1},a_t)\)

Pero SI medidas parciales de ella

 1.3 Aprendizaje por Refuerzo

Podemos aproximar \(\mathcal{T}_q\)

Utilizando las medidas  \((s_{t-1},a_t,s_t,r_t)\)

 1.3 Aprendizaje por Refuerzo

Necesitamos explorar el espacio de estados

\(\epsilon\)-Greedy

If \(\epsilon > rand \)
          \(a_t \leftarrow \) acción aleatoria
Else
          \( \displaystyle a_t \leftarrow \arg \max_{a'\in \mathcal{A}} [\mathcal{Q}_t(s_t,a') ]\)
End If

 1.3 Aprendizaje por Refuerzo

        Q-learning\((\mathcal{Q}^{*},s_0,tol,\alpha,\epsilon,N_t)\)
        \(\mathcal{Q} \gets \mathcal{Q}^{*}\)
        While \(error\leq tol \)

               \(s_0 \gets\) Estado inicial Aleatorio

               For \( t \in \{1,\dots,N_t\}\)
                      \( a_t \gets via \ \epsilon-Greedy\)
                      Actuar con \(a_t\) y medir \(r_{t}\) y \(s_{t+1}\)
                     \(\displaystyle \mathcal{Q}(s_t,a_t) \gets (1-\alpha)\mathcal{Q}(s_t,a_t) + \alpha\big[ r_t + \gamma \max_{a'\in \mathcal{A}}\mathcal{Q}(s_{t+1},a') \big] \)

                End For
         End While
         return\(\{a_t\}_{t>0}\)

 1.3 Aprendizaje por Refuerzo

 1.3 Aprendizaje por Refuerzo

 1.3 Aprendizaje por Refuerzo

Consideraciones

1. Necesitamos poder interactuar con el modelo. En la practica necesitamos un modelo simulado o un sistema real.
2. Medidas estáticas en el sistema no son suficientes, es necesario poder medir \((s_{t-1},a_t,s_t,r_{t})\), elegiendo \(a_t\).
3. Durante el desarrollo fue considerado la creación de un sistema de recomendación, sin embargo la falta de modelado impidió segui por este camino

2. Problema del Pastoreo 

2. Problema del Pastoreo 

• El problema fue formulado como problema de control óptimo
• Esta solución es poca robusta, ya que necesita medidas de las pociones de todos los agentes.
• Además depende del modelo que sigue el sistema

2. Problema del Pastoreo 

• Buscamos un política robusta que dependa de pocas medidas
• Conocemos un política heurística que funciona para varias configuraciones del estado.
• La política hurística este será nuestro punto de partida.
• El aprendizaje por refuerzo mejorar la política hurística. 

2. Problema del Pastoreo 

2.1 Modelo de Interacción

2.2 Aprendizaje por Refuerzo

2.3 Política Heusrística y pre-entrenamiento

2.4 Resultados Numéricos

2.1 Modelo de Interacción

 2.1 Modelo de Interacción

Variables de estado

Sea \(N_o\) número de ovejas y \(N_p\) número de perros

 2.1 Modelo de Interacción

Ecuación dinámica

 2.1 Modelo de Interacción

Fuerzas de Interacción

 2.1 Modelo de Interacción

Fuerzas de Interacción

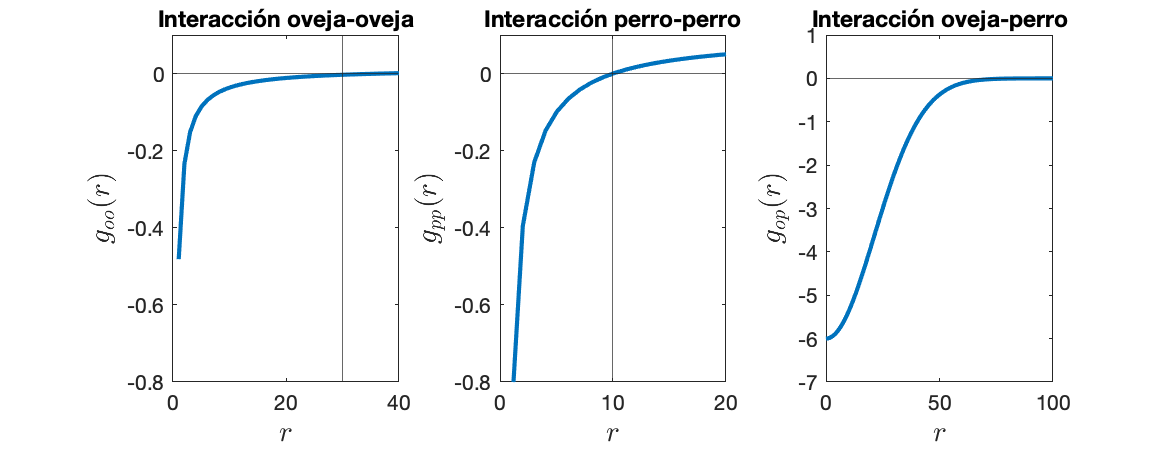
 2.1 Modelo de Interacción

2.2 Aprendizaje por refuerzo en el pastoreo

 2.2 Aprendizaje por refuerzo en P.

Estados y Acciones

 2.2 Aprendizaje por refuerzo en P.

Recompensa

• \(|| {u}_{om} - {u}_T||^2\) es el término que mide la distancia al punto objetivo
• \(|| cov(\bm{U}_o)||_{fro}^2\) es la norma de Frobenious de la matriz de co-varianza. 
•  \(\beta|| \bm{a}(t)||.^2\) es el coste de las acciones. 

 2.2 Aprendizaje por refuerzo en P.

Dinámica

• Supondremos que existe una distribución de probabilidad de transición entre un estado \({s}_t\) y \({s}_{t+1}\)

• La evolución del sistema esta determinada por el modelo de interacción de los agentes.
• Sin embargo, la ecuación diferencia de las medidas \(s_t\)nos es desconocida. 

 2.2 Aprendizaje por refuerzo en P.

 2.2 Aprendizaje por refuerzo en P.

• Dado que el espacio de estados es continuo y muy grande NO es posible utilizar Q-learning directamente.

\(\pi^*(s) \rightarrow \pi^\theta(s)\)

• La política deberá ser parametrizada

\(q^*(s) \rightarrow q^\omega(s)\)

• Podemos parametrizar la función valor

 2.2 Aprendizaje por refuerzo en P.

\( \displaystyle v^\pi(s) = \mathbb{E}_\pi \big[\sum_{t=0}^\infty \gamma^\tau R_{{\tau+1}}|S_0=s \big]\)

\( \displaystyle v_*(s) = \max_{\pi\in \Pi}  \mathbb{E}_\pi \big[\sum_{t=0}^\infty \gamma^\tau R_{{\tau+1}}|S_0=s \big]\)

\( \displaystyle v_*(s) = \max_{\pi\in \Pi}  v^\pi(s) = \max_{\theta\in \mathbb{R}^p}  v^{\pi_\theta}(s)\)

\( \theta_{k+1} \leftarrow \theta_k + \alpha  \nabla_\theta v^{\pi_\theta}(\bm{s}) \)

La política deberá ser parametrizada

Ascenso por gradiente

Para resolver el problema en espacios continuos 

 2.2 Aprendizaje por refuerzo en P.

Se puede comprobar

        \( \displaystyle q_\pi(s,a) =   \mathbb{E}_\pi \big[\sum_{t=0}^\infty \gamma^\tau R_{{\tau+1}}|S_0=s,A_0=0\big]\)

Donde

 2.2 Aprendizaje por refuerzo en P.

Dado una política \(\pi_\theta(s) \) podemos calcular \( q^{\pi_\theta}(s,a)\) mediante una función \(q_\omega(s,a)\) mediante Q-learning.

Teniendo un historial de \(M\) pasos

\(B = \{ \bm{s}_t^m,\bm{a}_t^m,\bm{s}_{t+1}^m,r_{t+1}^m\}_{m= 1}^{M}\)

 podemos encontrar los parámetros \(\omega\) de \(q_\omega(\bm{s},\bm{a})\) que mejor aproximen \(q^{\pi_\theta}(\bm{s},\bm{a})\) de la siguiente manera:

2.3 Política Heurística y Pre-entrenamiento

 2.3 P. Heurística y Pre-entrenamiento

\(        h_r(r) = - 1/r + 1/r_{min}^p \)

 \(  h_p(\phi) = 1 - cos(\phi)  \)

 2.3 P. Heurística y Pre-entrenamiento

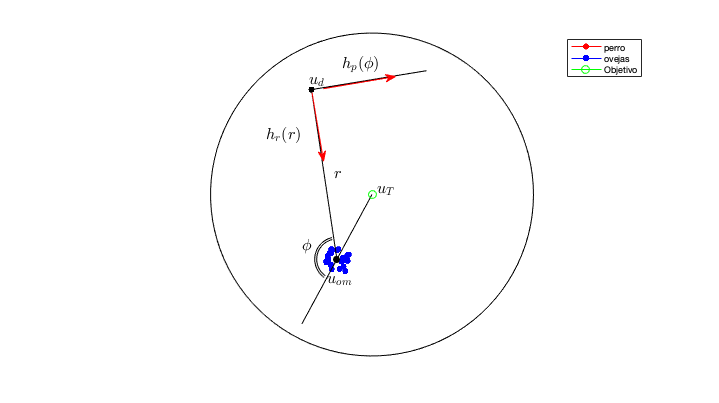
 2.3 P. Heurística y Pre-entrenamiento

• Generamos datos mediante simulación de la dinámica con la política hurísticas
• Con estos datos se entrenará los parámetros de \(\pi_\theta\)

 2.3 P. Heurística y Pre-entrenamiento

2.4 Resultados Numéricos

 2.4 Resultados Numéricos

¡Muchas Gracias!