Thinking in Twos

There are only 10 types of people in the world: those who understand binary and those who don't.

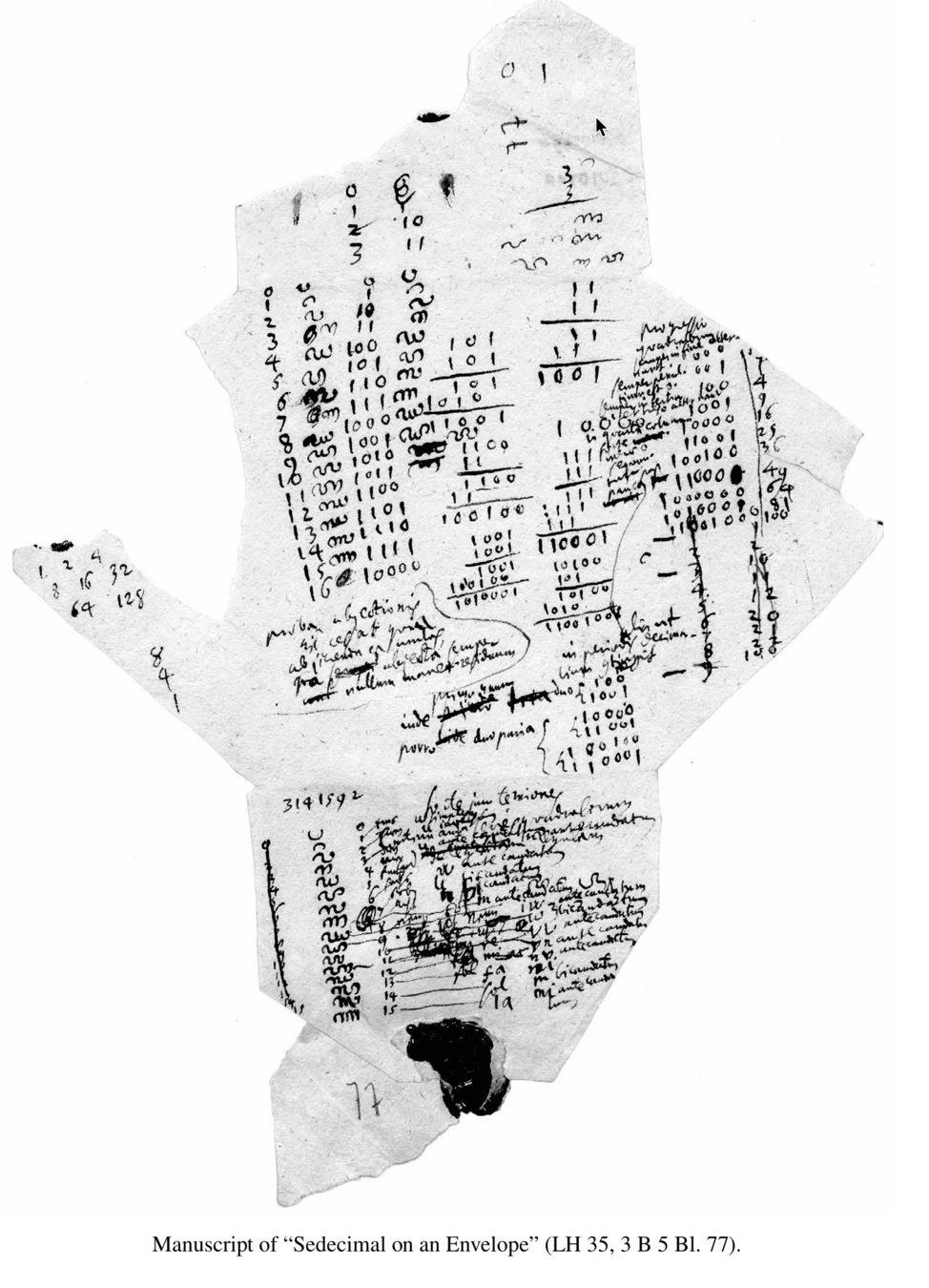
Fingers and positional number systems

Two hands, ten fingers.

What if we just used one hand? Write list of numbers if we count by fives instead of 10s. Write it out like above.

NOTICE: the fifth, like the tenth, is
going to be represented as 10.

What if we counted by 12?

NOTICE: we need another symbol or two. Something else for 10 and 11. But not 12 why?

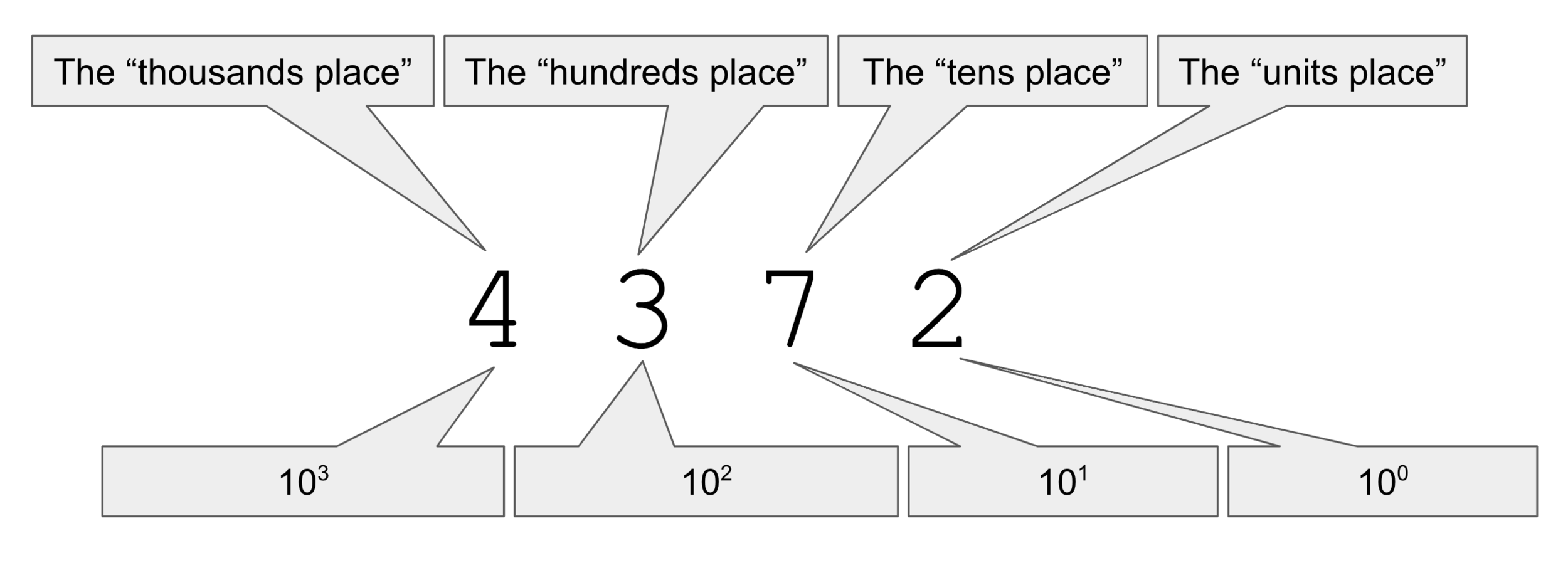
 0  1  2  3  4  5  6  7  8  9
10 11 12 13 14 15 16 17 18 19
20 21 22 23 24 25 26 27 28 29
30

00 01 02 03 04
10 11 12 13 14
20 21 22 23 24
30

 0  1  2  3  4  5  6  7  8  9  A  B
10 11 12 13 14 15 16 17 18 19 1A 1B
20 21 22 23 24 25 26 27 28 29 21 2B
30

Let's look at a few of these stack up next to one another

What're the patterns here?

\begin{array}{r} 101 \\ + 100 \\ \hline \\ \end{array}

\begin{array}{r} 1 \\ + 0 \\ \hline 1 \\ \end{array}

\begin{array}{r} 1 \\ + 1 \\ \hline 10\\ \end{array}

\begin{array}{r} 1 \\ - 1 \\ \hline 0\\ \end{array}

\begin{array}{r} (1)0 \\ - 1 \\ \hline 1\\ \end{array}

\begin{array}{r} 11011 \\ - 1011 \\ \hline \\ \end{array}

\begin{array}{r} 11011 \\ + 1011 \\ \hline \\ \end{array}

51_{10} = ?_2

19_{10} = ?_2

519_{10} = ?_2

111011001_{2} = ?_{10}

1101_{2} = ?_{10}

1001_{2} = ?_{10}

101100001_{2} = ?_{10}

Before we move on: Negative binary numbers mess with our heads

We could just write -0, -1, -10, etc. but we are thinking ahead and we imagine dealing with a minus sign is going to require a much smarter robot than we are prepared to build.

Suppose you have a clock and you want to set it back an hour in the fall when daylight savings time ends but your clock only winds forward. How many hours should you wind it forward?

What if you want to set it to California time, 3 hours back?

Move forward 9

There's a pattern here:

So this means I can take the numbers 0 - 11 and use half of them (11,10,9,8,7,6) as "minus numbers" (specifically -1, -2, -3, -4, -5, and -6). So, to turn my clock back 6 hours, I turn it ahead 6 hours, etc.

-1

-2

-3

-4

-5

-6

"Turn ahead" means "add" and the thing about a clock is that it does modular arithmetic, specifically, mod 12.

You'll notice that I fiddled with the clock and turned 12 into 0.

Back to binary. We can use a similar trick with binary numbers. Let's imagine our clock has sixteen hours instead of 12.

So, if I want to subtract 7 I just add 9. Weird, but it works because of modular arithmetic, in this case mod 16.

But what does this have to do with binary arithmetic? Remember, we are worried about how to do negative numbers in binary.

We can just let some of the numbers from 1 to 16 stand for negative numbers

-1

-2

-3

-4

-5

-6

-7

-8

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15

0 1 2 3 4 5 6 7 -8 -7 -6 -5 -4 -3 -2 -1

-1

-2

-3

-4

-5

-6

-7

-8

the "sign bit"

Let's line things up

flip the bits

add 1

1101
+1
----
1110

-1

-2

-3

-4

-5

-6

-7

-8

"Two's Complement" And Now the MAGIC

write both in 2's complement form

and

ADD

3
-5
----
-2

0011
+1011
----
1110

result in 2s complement is -2

Compute the 2s complement

6
-7
----
-1

Trick question, 17. We have been working with 4 bit numbers with the "most significant bit" (why do we call it that?) used as a sign bit. We could do 2s complement with any length but we need to stick with one. We need to use enough bits to represent the range of numbers we are working with and typically we do powers of two: 4, 8, 16, etc.

17
-9
----
8

35
-42
----
-7

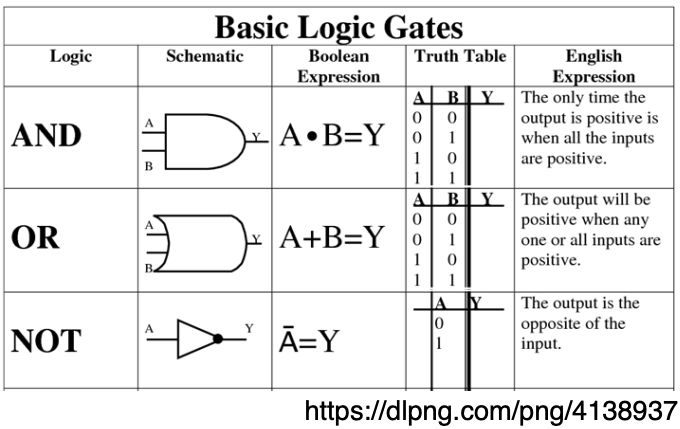
Basic Logic

Label statements with variables. Statements can be TRUE or FALSE.

A = The sun is shining.

not A = The sun is not shining.

A and B = The sun is shining and I can see a dog.

A or B = The sun is shining or I can see a dog.

B = I see a dog.

not B = I do not see a dog.

Compound statements can be created by combining statements with logical operators AND, OR, and NOT

not(A and B) = It is not the case that both the sun is shining and I can see a dog.

not(A or B) = It is false that the sun is shining or I can see a dog.

Logical operators are defined by their TRUTH TABLES

\begin{array}{c c | c} A & B & A \land B \\ \hline F & F & F \\ F & T& F \\ T & F& F \\ T& T & T\\ \end{array}

a column for each simple statement (variable)

a row for each possible combination of truth values for the simple statements (variables)

a column for the result

This is the DEFINITION of AND - it's only true if both the operands are true

not(A and B) = It is not the case that both the sun is shining and I can see a dog.

not(A or B) = It is false that the sun is shining or I can see a dog.

\begin{array}{c c | c} A & B & \neg (A \land B)\\ \hline F & F & T \\ F & T& T \\ T & F& T \\ T& T & F\\ \end{array}

A or B = The sun is shining or I can see a dog.

\begin{array}{c c | c} A & B & A \lor B \\ \hline F & F & F \\ F & T& T \\ T & F& T \\ T& T & T\\ \end{array}

\begin{array}{c c | c} A & B & \neg (A \lor B)\\ \hline F & F & T \\ F & T& F \\ T & F& F \\ T& T & F\\ \end{array}

Fill in the truth table for the expression not A and not B

\begin{array}{c c | c} A & B & \neg A \land \neg B\\ \hline F & F & \\ F & T& \\ T & F& \\ T& T & \\ \end{array}

Fill in the truth table for the expression A or not B

\begin{array}{c c | c} A & B & A \lor \neg B \\ \hline F & F & \\ F & T& \\ T & F& \\ T& T & \\ \end{array}

If A = The sun is shining and B = I see a dog, how do you read A or not B.

Fill in the truth table for the expression not (A or B). Proceed STEPWISE!

\begin{array}{c c | c|c} A & B & A \lor B & \neg (A \lor B)\\ \hline F & F & & \\ F & T& & \\ T & F& & \\ T& T & & \\ \end{array}

Fill in the truth table for the expression not A or not B

\begin{array}{c c |c|c| c} A & B & \neg A & \neg B & \neg A \lor \neg B\\ \hline F & F & \\ F & T& \\ T & F& \\ T& T & \\ \end{array}

Fill in the truth table for the expression not (A and B).

\begin{array}{c c | c|c} A & B & A \land B & \neg (A \land B)\\ \hline F & F & & \\ F & T& & \\ T & F& & \\ T& T & & \\ \end{array}

Fill in the truth table for the expression not A and not B

\begin{array}{c c | c} A & B & \neg A \land \neg B\\ \hline 0 & 1 & \\ 0 & 1& \\ 1 & 0& \\ 1 & 1 & \\ \end{array}

Fill in the truth table for the expression A or not B

\begin{array}{c c | c} A & B & A \lor \neg B \\ \hline 0 & 0 & \\ 0 & 1& \\ 1 & 0& \\ 1& 1 & \\ \end{array}

Fill in the truth table for the expression not (A or B). Proceed STEPWISE!

\begin{array}{c c | c|c} A & B & A \lor B & \neg (A \lor B)\\ \hline 0 & 1 & \\ 0 & 1& \\ 1 & 0& \\ 1 & 1 & \\ \end{array}

Fill in the truth table for the expression not A or not B

\begin{array}{c c |c|c| c} A & B & \neg A & \neg B & \neg A \lor \neg B\\ \hline 0 & 1 & \\ 0 & 1& \\ 1 & 0& \\ 1 & 1 & \\ \end{array}

Fill in the truth table for the expression not (A and B).

\begin{array}{c c | c|c} A & B & A \land B & \neg (A \land B)\\ \hline 0 & 1 & \\ 0 & 1& \\ 1 & 0& \\ 1 & 1 & \\ \end{array}

Let's repeat the previous page, but from now on we will use 0 for FALSE and 1 for TRUE

Up to now we were using the mathematical and logical symbols for AND, OR, and NOT. Let's make three changes.

First, instead of the bent bar prefix to signify not, let's just draw a line over a variable to indicate that it has been negated with not.

Let's simplify our notation a little.

(A \land \neg B \land C) \lor (\neg A \land \neg B \land \neg C)

A \overline{B} C + \overline{A} \overline{B} \overline{C}

\neg (\text{it is sunny})

\overline{\text{it is sunny} }

A \land \neg B

A \land \overline{B}

So, is and can be written as .

First, instead of the wedges for AND and OR we will use a dot for AND and a plus sign for OR.

So, becomes .

A \land B \lor C

A \cdot B + C

And, in fact, we generally just omit the dot and put two variables next to each other when we mean AND.

So, becomes .

If A="today is Tuesday" and B="Today is Thursday" and C="The sun is shining", write an expression that means "it's either a sunny Tuesday or a cloudy Thursday."

If A="today is Tuesday" and B="Today is Thursday" and C="The sun is shining" and D="I see a dog", write an expression that means "it's either a cloudy Tuesday or Wednesday or it's a sunny day with a dog in sight or it's just cloudy and there are no dogs."

\begin{array}{c c c | c c c | c | c | c} A & B & C & \overline{A} & \overline{B} & \overline{C} & A\,\overline{B}\,C & (A\,\overline{B}\,C) + (\overline{A}\,\overline{B}\,\overline{C} ) & \overline{A}\,\overline{B}\,\overline{C} \\ \hline 0 & 0 & 1 \\ 0 & 0 & 1 \\ 0 & 1 & 0 \\ 0 & 1 & 1 \\ 1 & 0 & 1 \\ 1 & 0 & 1 \\ 1 & 1 & 0 \\ 1 & 1 & 1 \\ \end{array}

Fill in the truth table for the expression A and not B and C or not A and not B and not C.

Build truth tables for expressions by stepwise refinement.

First problem: how should we group the operands in this expression?

A \cdot \overline{B} \cdot (C + \overline{A}) \cdot \overline{B} \cdot \overline{C}

If we think of AND as multiplication and OR as addition (we'll see why this is the right approach later), then the usual precedence holds. NOT goes first, then AND, then OR. So the right interpretation is this

(A \cdot \overline{B} \cdot C) + (\overline{A} \cdot \overline{B} \cdot \overline{C})

(A \, \overline{B} \, C) + (\overline{A} \, \overline{B} \,\overline{C})

Let's get back to binary math now that we know we only need to worry about addition.

For a single bit, here is the whole show:

\begin{array}{r} 0 \\ + 0 \\ \hline 0 \\ \end{array}

\begin{array}{r} 0 \\ + 1 \\ \hline 1\\ \end{array}

\begin{array}{r} 1 \\ + 0 \\ \hline 1 \\ \end{array}

\begin{array}{r} 1 \\ + 1 \\ \hline 10\\ \end{array}

STOP+THINK: Do you notice any pattern in the sequence of numbers we are adding?

\begin{array}{r} A \\ + B \\ \hline CS \\ \end{array}

Let's put a leading 0 in the first three to keep things symmetrical.

\begin{array}{r} 0 \\ + 0 \\ \hline 00 \\ \end{array}

\begin{array}{r} 0 \\ + 1 \\ \hline 01\\ \end{array}

\begin{array}{r} 1 \\ + 0 \\ \hline 01 \\ \end{array}

\begin{array}{r} 1 \\ + 1 \\ \hline 10\\ \end{array}

STOP+THINK: Each of these is a version of .

Any idea why we might be using "C" and "S" here??

\begin{array}{r} A \\ + B \\ \hline CS \\ \end{array}

\begin{array}{c c | c | c} A & B & C & S\\ \hline 0 & 1 & \\ 0 & 1 & \\ 1 & 0 & \\ 1 & 1 & \\ \end{array}

Can you put this information into a truth table?

Let's put a leading 0 in the first three to keep things symmetrical.

\begin{array}{r} 0 \\ + 0 \\ \hline 00 \\ \end{array}

\begin{array}{r} 0 \\ + 1 \\ \hline 01\\ \end{array}

\begin{array}{r} 1 \\ + 0 \\ \hline 01 \\ \end{array}

\begin{array}{r} 1 \\ + 1 \\ \hline 10\\ \end{array}

STOP+THINK: Each of these is a version of .

Any idea why we might be using "C" and "S" here??

\begin{array}{r} X \\ Y\\ + Z\\ \hline CS \\ \end{array}

\begin{array}{c c | c | c} A & B & C & S\\ \hline 0 & 1 & \\ 0 & 1 & \\ 1 & 0 & \\ 1 & 1 & \\ \end{array}

Can you put this information into a truth table?

A	B	C	S
0	0	0	0
0	1	0	1
1	0	0	1
1	1	1	0

looks like
A AND B

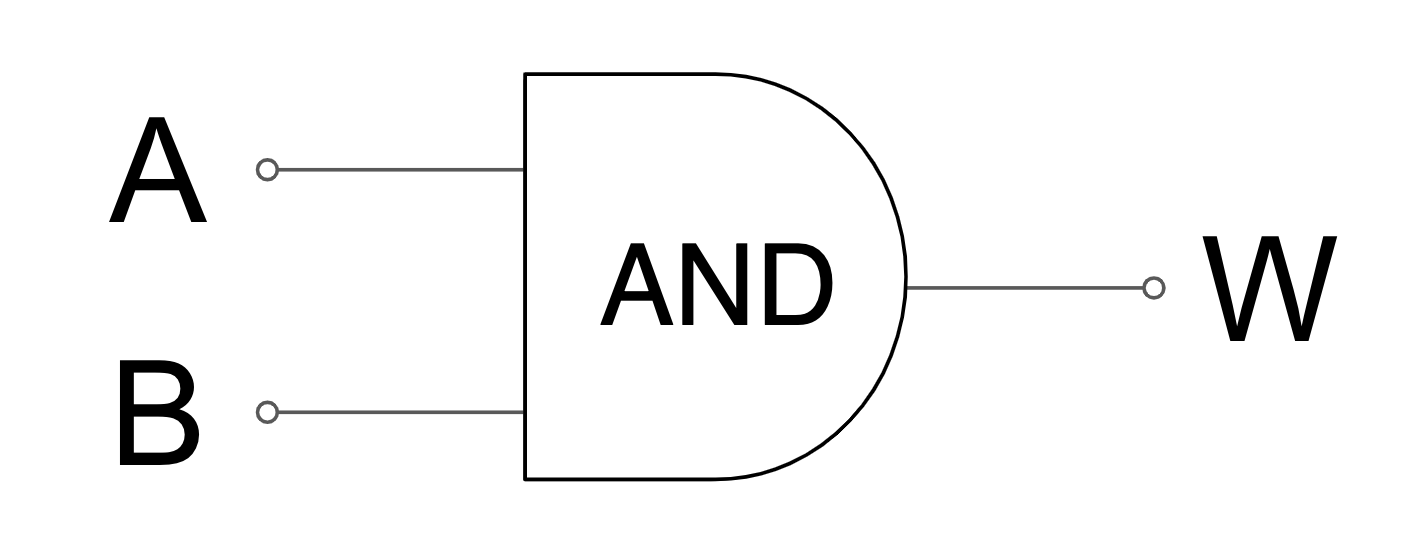
C

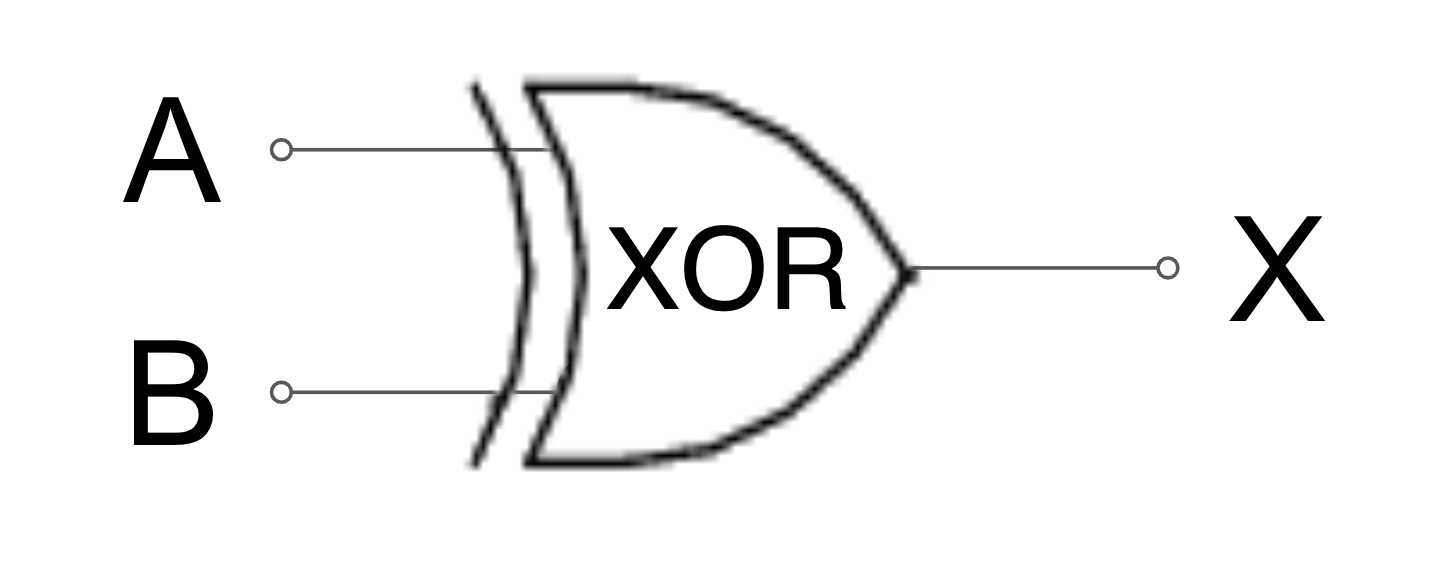
S

looks like
A XOR B

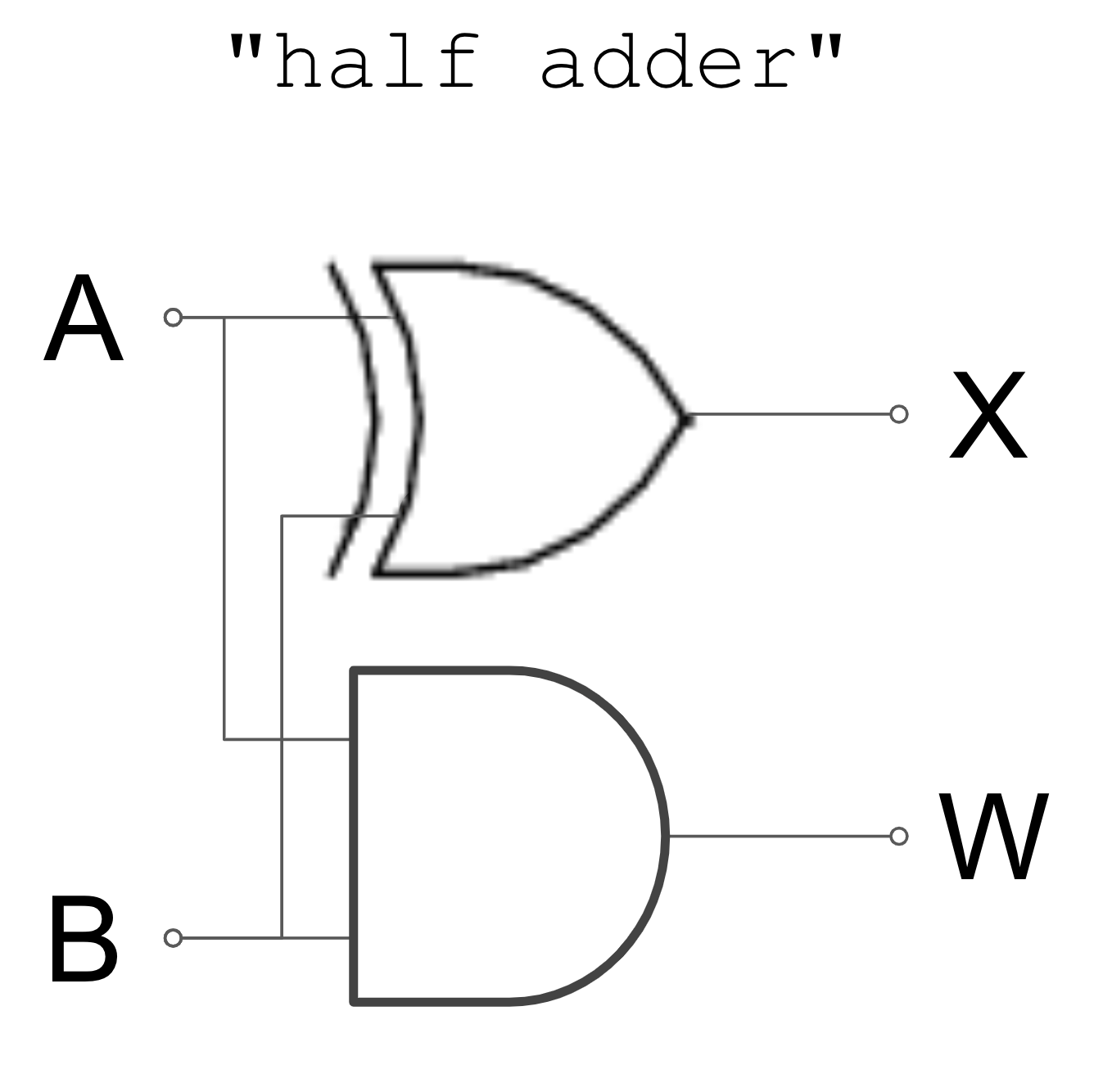
STOP+TRY: build the half adder circuit. Use switches for inputs and bulbs for outputs.

\begin{array}{c c c | c | c | c } A & B & C & A \, B \, \overline{C} & \overline{A} \, \overline{B} \, C & A \, B \, \overline{C} + \overline{A} \, \overline{B} \, C \\ \hline 0 & 0 & 1 \\ 0 & 0 & 1 \\ 0 & 1 & 0 \\ 0 & 1 & 1 \\ 1 & 0 & 1 \\ 1 & 0 & 1 \\ 1 & 1 & 0 \\ 1 & 1 & 1 \\ \end{array}

Consider the following scenario. We have three variables A,B,C. If A and B are 0 and C is 1 the result is 1. If A and B are 1 and C is 0, then the result is 1. Otherwise the result is zero.

Write out the expression for result and construct the truth table.

Thinking in Twos

C

S

STOP+THINK
Could we do math
with Donuts?

AND, OR

CT2025 Binary 1

CT2025 Binary 1

Dan Ryan PRO

Thinking in Twos

C

S

STOP+THINK Could we do math with Donuts?

AND, OR

CT2025 Binary 1

More from Dan Ryan

STOP+THINK
Could we do math
with Donuts?